Security Valuation – CA Final SFM Study Material

Security Valuation – CA Final SFM Study Material is designed strictly as per the latest syllabus and exam pattern.

Security Valuation – CA Final SFM Study Material

Part – 1 (Theory)

Question 1.
Write a short note on Zero coupon bonds [May 2012] [4 Marks]
Answer:
Zero coupon bonds are issued by Banks, Government and Private Sec-tor companies. These bonds do not pay interest during the life of the bonds. Instead, they are issued at discounted price to their face value, which is the amount a bond will be worth when it matures or comes due. When it matures, the investor receives a lump sum amount equal to the initial investment plus interest that has been accrued on the investment made. The maturity dates on zero coupon bonds are usually long term. Bonds issued by corporate sector carry a potentially higher degree of risk, depending on the financial strength of the issuer and longer maturity period, but they also provide an opportunity to achieve a higher return.

Question 2.
Write a short note on Traditional & Walter Approach to Dividend Policy. [May 2014] [4 Marks]
Answer:
Traditional approach:
It is also known as the “The Graham and Dodd model” as it was expounded by him. According to the model, the stock market places considerably more weight on dividends than on retained earnings. This is expressed quantitatively in the following valuation model:
P = m(D + E/3)
Where, P = Market price of the share
D = Dividend per share
E = Earnings per share
m = a multiplier.

This model is based on the following assumptions:
(a) Investors are rational
(b) Under conditions of uncertainty, they turn risk averse.
Under this model, the weight attached to dividends is equal to four times the weight attached to retained earnings. The weights provided by Graham and Dodd are based on their subjective judgment and not derived from any empirical analysis.
Investors discount distant dividends at a higher rate than they discount nearby dividend. This is because nearby dividends are more certain than distant dividends.

Walter approach:
The Walter’s Model propounded in 1963 by John E Walter supports the doc-trine that dividends are relevant. The investment policy of the firm cannot be separated from its dividend policy and both are interlinked. The choice of an appropriate dividend policy affects the value of any firm. It is based on the following assumptions:
(a) The firm is an all equity firm.
(b) The firm will use only retained earnings to finance its investments.
(c) The rate of return on investment is constant and so is the cost of equity. This means that with every additional investment, business risk remains unaltered.
(d) All earnings are either distributed or retained internally.
(e) The firm has a perpetual or very long life.
(f) Earnings and dividends don’t change over the life of the firm.

Walter argued that the market price of a share is the sum of the present value of the following two cash flow streams:

• Infinite stream of constant future dividends.
• Infinite stream of capital gains.

Walter model is based on the premise that there is a relationship between the return on a firm’s investment or its internal rate of return (r) and its cost of capital (ke). The firm would have an optimum dividend policy which will be determined by the relation between (r) and (ke). If r is greater than ke, the firm should retain the earnings and if r is less than ke, it must distribute the earnings.

Question 3.
Why should the duration of a coupon carrying bond always be less than the time to its maturity? [May 2009] [3 Marks]
Answer:
The concept of duration can be defined as the percentage change in price of a bond for a 100 basis point change in interest rates. However, there is another concept of duration ie. the time concept of duration according to which duration is nothing but the average time taken by an investor to collect his/her investment. It is the weighted average time to receive the present value of the bond. Therefore, if an investor receives a part of his/her investment over the time on specific intervals before maturity, the investment will offer him the duration which would be lesser than the maturity of the instrument. Higher the coupon rate, lesser would be the duration. The duration of a Zero coupon bond is always equal to its maturity period.

Question 4.
Write a note on buy-back of shares by companies and what is the impact on P/E Ratio upon buy-back of shares? [Nov. 2019 (Old Syllabus)] [4 Marks]
Answer:
Buy-Back of Shares: The buy-back of shares means the repurchase of its own shares by a company and to return money to the holders of these shares. The cash is exchanged for a reduction in the number of outstanding shares. Since this process involves outflow of cash resources, it is adopted when the company has sufficient cash resources. The buy-back is a method of financial engineering which enables the company to go back to its shareholders and offers to purchase from them the shares they hold. However, the companies have to fulfil some legal conditions for buy-back of shares.

Impact of Buy-Back on P/E Ratio:
P/E Ratio is given by the following formula :
P/E = \(=\frac{\text { Market Price of the Share }}{\text { Earnings per Share }}\)
The buy back of shares by the company reduces the number of shares. In this case if the earnings remain constant, there is a rise in the Earnings Per Share ie. EPS.
After buy back, the market price of the share generally increases. Thus, there is increase in Market price of share Le. MPS.
As the numerator and denominator in the formula tend to increase, the impact on P/E will depend upon the quantum of relative increase in the two factors.

Part – 2 (Numerical Problems)

Question 1.
An investor is considering the purchase of the following Bond:

Face Value	₹ 100
Coupon rate	11%
Maturity	3 years

(i) If he wants a yield of 13%, what is the maximum price he should be ready to pay for?
(ii) If the Bond is selling for ₹ 97.60, what would be his yield? [Nov. 2009] [4 Marks]
Answer:
(i) Calculation of Maximum price
The present value of future inflows (comprising both interest as well as redemption value) discounted at 13% is the maximum price the investor would be ready to pay.
Annual Interest (I) = Rs. 100 × \(\frac{11}{100}\) = Rs. 11
Redemption Value (RV) = Rs. 100
Maturity Period (n) = 3 Years
Accordingly, Present value of future inflows can be calculated as
= ₹ 11 × PVIFA_{(13%, 3)} + ₹ 100 PVIF_{(13%, 3)}
= ₹ 11 × 2.361 + ₹ 100 × 0.693
= ₹ 25.97 + 69.30
= ₹ 95.27
The maximum price that the investor is ready to pay is Rs. 95.27.

(ii) Calculation of yield
It may be noted that the price of bond and yield/return are inversely related. The fair value is Rs. 95.28 at 13% yield. It means, if the bond is selling at higher than this fair value at Rs. 97.60, the return will be less than 13%.

Let us find out approximate yield:

= 0.1194 or 11.94%
The present value of future inflows (comprising both interest as well as Value at 12%
= ₹ 11 × PVIFA(12%3) + 100 × PVIF(12% 3)
= ₹ 11 × 2.402 + ₹ 100 × 0.712
= ₹ 26.42 + ₹ 71.20
= ₹ 97.62
This value is almost equal to the price of ₹ 97.60. Therefore, the YTM of the bond would be 12%.

Question 2.
The Nominal value of 10% Bonds issued at par by M/s SK Ltd. is Rs. 100. The bonds are redeemable at Rs. 110 at the end of year 5.
(I) Determine the value of the bond if required yield is : [Nov. 2019 Old Syllabus [5 Marks]]
(i) 8%
(ii) 9%
(iii) 10%
(iv) 11%
(II) When will the value of the bond be highest ?
Given below are Present Value Factors :

Answer:
Given
Coupon rate 10%
Face value Rs. 100
Redemption Value Rs. 110
Life 5 yrs.
(I) Value of the bond if required yield is

(II) The price and yield are inversely related. Therefore, the highest price will be at the lowest yield. In the given case the value of the bond will be highest when yield is 8%.

Question 3.
Calculate Market Price of:
(i) 10% Government of India security currently quoted at ₹ 110, but interest rate is expected to go up by 1%.
(ii) A bond with 7.5% coupon interest, Face Value ₹ 10,000 & term to maturity of 2 years, presently yielding 6%. Interest payable half yearly. [Nov. 2010] [5 Marks]
Answer:
(i) Current yield:
= (Coupon Interest/Market Price) × 100 = (10/110) × 100 = 9.09%
When current yield go up by 1%:
Expected Yield = Current Yield + 1% = 9.09% + 1 = 10.09%
Calculation of new market price at a yield of 10.09%:
Yield =(Coupon Interest/Market Price) × 100 Or 10.09
= 10/Market Price × 100 New Market Price
= ₹ 99.11

(ii) Market Price of Bond:
The market price of the bond shall be the present value of future inflows, which comprises interest as well as redemption value.
Market Price = P. V. of Interest + P. V. of Principal
Half-yearly Interest (I) = Rs. 10,000 × \(\) = Rs. 375
Redemption Value (RV) = Rs. 10,000
Maturity Period (n) = 2 Years or 4 half Years
YTM (r) = 6% p.a. or 3% half yearly
Market Price = ₹ 375 × PVIFA_(3%4) + ₹ 10,000 × PVIF_(3%4)
= (₹ 375 × 3.7171) + (₹ 10,000 × .8885)
= ₹ 1,394 + ₹ 8,885
= ₹ 10,279

Tutorial Note:
Since, the coupon (7.5%) is higher than YTM (6%), therefore the bond will be selling at premium i.e. above Rs. 10,000.

Question 4.
Based on the credit rating of the bonds, A has decided to apply the following discount rates for valuing bonds:

Credit rating	Discount rate
AAA	364-day T-bill rate + 3% spread
AA	AAA + 2% spread
A	AAA + 3% spread

He is considering to invest in a AA rated ₹ 1,000 face value bond currently selling at ₹ 1,025.86. The bond has five years to maturity and the coupon rate on the bond is 15 per cent per annum payable annually. The next inter-est payment is due one year from today and the bond is redeemable at par.
(Assume the 364-day T-bill rate to be 9 per cent).
You are required to calculate:
(i) The intrinsic value of the bond for A. Should he invest in the bond?
(ii) The Current Yield (CY) and
(iii) The Yield to Maturity (YTM) of the bond. [Nov. 2011] [8 Marks]
Answer:
(i) Calculation of Intrinsic Value of the bond:
As per table given in the question, the appropriate discount rate for valuing the AA rated bond for A is:
YTM = 996 + 396 + 2% = 1496
The other parameters are:
Annual Interest (I) = 1596 of Rs. 1,000 = Rs. 150
Redemption Value (RV) = Rs. 1,000
Maturity Period (n) = 5 Years
Accordingly, Intrinsic Value of future inflows can be calculated as = ₹ 150 × PVIFA(14%5) + ₹ 1,000 × PVIF(14%>5)
= ₹ 150 × 3.4331 + ₹ 1,000 × 0.5194
= ₹ 514.96 + ₹ 519.40 = ₹ 1,034.36
The current market value (Rs. 1,025.86) is less than the intrinsic value (Rs. 1,034.36) of the bond. Therefore, the bond is underpriced. So, Mr. A should buy the bond.

(ii) Calculation of Current Yield (CY):
Current yield = Annual Interest/Price = ₹ 150/₹ 1,025.86
= 14.6296

(iii) Calculation of Yield to Maturity (YTM):
Since, the coupon rate is 15% and bond is redeemable at par, therefore the price of the bond at 15% YTM will be Rs. 1,000.

Yelid	Value (Rs)
15%	1,000
14%	1,034.36

YTM at Rs, 1025.86 can be calculated using interpolation as per the manner given below.
By interpolation, the YTM is
= 14% + \(\frac{34.36-25.86}{34.36}\) × (15% – 14%)
= 14% + \(\frac{8.5}{34.36}\)%
= 14.24796

Question 5.
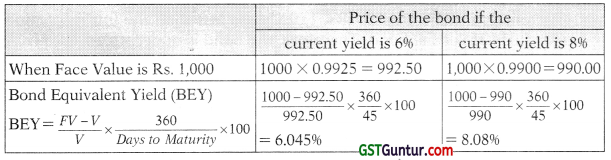
A bond is held for a period of 45 days. The current discount yield is 6 per cent per annum. It is expected that current yield will increase by 200 basis points and current market price will come down by Rs. 2.50.
Calculate
(i) Face Value of the Bond
(ii) Bond Equivalent yield. [May 2017] [4 Marks]
Answer:
(i) Let the Face value of bond be Re. 1

The difference in bond price due to 200 basis increase in interest rates is a decrease of Re. 0.0025. Therefore, by applying unitary method, if the actual difference is Rs. 2.50 the face value of the bond will be \(\frac{2.5}{0.0025}\) × 1 = Rs. 1,000
Face Value of the Bond = Rs. 1,000

(ii) Bond Equivalent yield

Question 6.
Bright Computers Limited is planning to issue a debenture series with a face value of ₹ 1,000 each for a term of 10 years with the following coupon rates:

Years	Rates
1-4	8%
5-8	9%
9-10	13%

The current market rate on similar debenture is 15% p.a. The company proposes to price the issue in such a way that a yield of 16% compounded rate of return is received by the investors. The redeemable price of the debenture will be at 10% premium on maturity. What should be the issue price of debenture?
PV @ 16% for 1 to 10 years are: .862, .743, .641, .552, .476, .410, .354, .305, .263, .227 respectively. [May 2016] [5 Marks]
Answer:
The issue price of the debentures will be the sum of present value of interest payments during 10 years and present value of redemption of debenture.
Interest (first 4 Years) = Rs. 1,000 @ 8% = Rs. 80
Interest (Next 4 Years) = Rs. 1,000 @ 9% = Rs. 90
Interest (Next 2 Years) = Rs. 1,000 @ 13% = Rs. 130
Redemption Value (10th Year) = Rs. 1,100
Maturity = 10 Years YTM = 16%

The cash inflows of the interest part are not constant throughout the period and the present value factors are given in the question. Therefore, it would be better to solve in the following tabular form.

Years	Cash outflow (Rs.)	PVF @ 16%	PV
1	80	0.862	68.96
2	80	0.743	59.44
3	80	0.641	51.28
4	80	0.552	44.16
5	90	0.476	42.84
6	90	0.410	36.90
7	90	0.354	31.86
8	90	0.305	27.45
9	130	0.263	34.19
10	130	0.227	29.51
10	1,100 (RV)	0.227	249.70
			676.29

The company should issue the debentures at a price at ₹ 6/6.29.

Question 7.
Consider two bonds, one with 5 years to maturity and the other with 20 years to maturity. Both the bonds have a face value of ₹ 1,000 and coupon rate of 8% (with annual interest payments) and both are selling at par.
(i) Assume that the yields of both the bonds fall to 6%, whether the price of bond will increase or decrease?
(ii) What percentage of this increase/decrease comes from a change in the present value of bond’s principal amount and what percentage of this increase/decrease comes from a change in the present value of bond’s interest payments? [May 2009] [8 Marks]
Answer:
(i) The price of bond and yield are inversely related. Since the yield falls to 6%, the price of bonds will increase. The increase in price of the bond with higher maturity period will be higher.

If yield falls to 6%

Price of 5 years bond
= ₹ 80 × PVIFA(6% 5) + ₹ 1,000 × pvif(6% 5) = (₹ 80 × 4.2124) + (₹ 1,000 × 0.7473) = 336.99 + 747.30 = ₹ 1,084.29	Increase in price Rs. 84.29
Price of 20 years bond
= ₹ 80 × pvifa(6%20) + ₹ 1,000 × PVIF(6%20) = (₹ 80 × 11.4699) + (₹ 1,000 × 0.3118) = 917.59 + 311.80 = ₹ 1,229.39	Increase in price Rs. 229.39

(ii) Price increase in Bond:
(a) Due to change in the present value of bond’s principal amount:

Price of 5 years bond
= Principal × [PVIF(6%,5) – PVIF(8%,5)] = 1,000 × [0.7473 – 0.6806] = Rs. 66.70	Percentage Increase \( \frac{\text { Rs. } 66.70}{\text { Rs. } 84.29} \) × 100 = 79.13%
Price of 20 years bond
= Principal × [PVIF(6%,5) – PVIF(8%,5)] = 1,000 × [0.3118 – 0.2145] = Rs. 97.30	Percentage Increase \( \frac{\text { Rs. } 97.30}{\text { Rs. } 229.39} \) × 100 = 42.42%

(b) Due to change in the present value of bond’s Interest amount:

Price of 5 years bond
= Interest × [PVIF(6%,5) – PVIF(8%,5)] = 80 × [4.2124 – 3.9927] = Rs. 17.59	Percentage Increase \( \frac{\text { Rs. } 17.59}{\text { Rs. 84.29 }} \) × 100 = 20.87%
= Interest × [PVIF(6%,5) – PVIF(8%,5)] = 80 × [11.4699 – 9.8181] = Rs. 132.14	Percentage Increase \( \frac{\text { Rs. } 132.14}{\text { Rs. } 229.39} \) × 100 = 57.58%

Tutorial Note:
The segment of increase in the price of the bond due to interest part is higher mease of bond with higher maturity.

Question 8.
Pet feed pic has outstanding, a high yield Bond with the following features:

Face value	£10,000
Coupon	10%
Maturity period	6 years
Special feature	Company can extend the life of Bond to 12 years.

(a) If an investor expects that interest will be 8%, six years from now then how much he should pay for this bond now.
(b) Now suppose, on the basis of that expectation, he invests in the Bond,
but interest rate turns out to be 12%, six years from now, then what will be his potential loss/gain if company extends the life of bond another 6 years [RTP Nov. 2018]
Answer:
(a) If the current interest rate is 896, the company will not extend the duration of Bond and the maximum amount the investor would be ready to pay will be:
= £ 1,000 PVIFA (8%, 6) + £10,000 PVIF (8%,6)
= £1,000 × 4.623 + £10,000 × 0.630
= £4,623 + £ 6,300
= £10,923

(b) If the current interest rate is 1296, the companies will extend the duration of Bond. After six year the value of Bond will be =£ 1,000 PVIFA (1296,6) + £10,000 PVIF (1296,6)
= £1,000 × 4.111 + £10,000 × 0.507
= £ 4,111 + £ 5,070
= £ 9,181
Potential gain = £9,181 – £10.923 = -£1,742
Thus, potential loss will be £1,742

Question 9.
On 31st March 2013, the following information about bond is available:

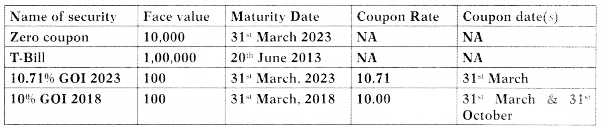
i. If 10 year yield is 7.5% p.a., what price the Zero coupon Bond would fetch on 31st March 2013?
ii. What will be the annualized yield if the T-Bill is traded @ Rs. 98,500?
iii. If 10.71% GOI 2023 Bond having yield to maturity is 8% what price would it fetch on April 1, 2013 (after coupon payment on 31st March)?
iv. If 10% GOI 2018 Bond having yield to maturity is 8%, what price would it fetch on April 1, 2013 (after coupon payment on 31st March)? [May 2015][8 Marks]
Answer:
(i) Price of Zero coupon bond on 31.3.2013:
= 10,000 PVIF (7.5%, 10)
= 10,000 × 0.4852
= Rs. 4,852

(ii) Annualized yield on T-Bill = \(\frac{F-P}{P} \times \frac{365}{M}\) × 100
\(\frac{1,00,000-98,500}{98,500} \times \frac{365}{81}\) × 100 = 6.

(iii) 10.71 PVIFA (8%, 10) + 100 PVIF (8%, 10)
= 10.71 × 6.7101 + 100 × 0.4632
= 71.87 + 46.32
= Rs. 118.19

(iv) 5 PVIFA (496,10) + 100 PVIF (4%, 10)
= 5 × 8.111 + 100 × 0.6756
= 40.56 + 67.56
= Rs.108.12

Question 10.
Consider a bond selling at its par value of ₹ 1,000, with 6 years to maturity and a 7% coupon rate (with annual interest payment).
(a) What is bond’s duration? [May 2009] [6 Marks]
(b) If the YTM of the bond in (a) above increases to 10%, how it affects the bond’s duration? And why? [3 Marks]
Answer:
(i) Determination of Duration of the Bond:
The following steps are to be taken:
Step 1: Calculation of YTM (Yield to maturity).
Since, the coupon rate is 7°-6 and bond is redeemable at par, and the price of the bond is Rs. 1,000 i.e. the bond is selling at par therefore the YTM ‘ will be 7%.

Step 2 : Calculation of Duration.
The duration of a bond is the weighted average of the time it takes to return the investor’s money. The present values of cash flows are to be taken as weights (w).

Year Cash flows(Rs.) PVIF@ PV of cash flows (?) Weighted Time

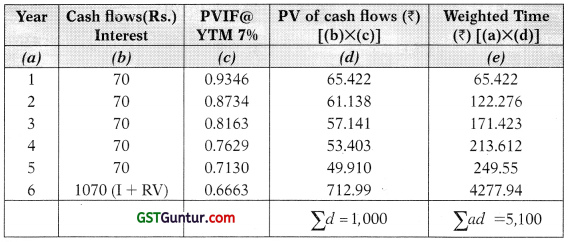
Duration = \(\frac{\text { Weighted Time }}{\text { Purchase Price }}=\frac{\sum a d}{\sum d}=\frac{\text { Rs. } 5,100}{\text { Rs.1,000 }}\) = 5.10 Years

Alternative Method for determination of Duration:

Formula method	Where,
Duration = \( \frac{1+y}{y-}-\frac{(1+y)+\text { Period }(c-y)}{c\left[(1+y)^{\text {Period }}-1\right]+y} \)	y = Yield to maturity c = Coupon rate

Duration = \(\frac{1+0.07}{0.07}-\frac{(1+0.07)+6(0.07-0.07)}{0.07\left[(1+0.07)^6-1\right]+0.07}\)
= \(\frac{1.07}{0.07}-\frac{1.07}{0.10505}\)
= 15.2857 – 10.1855 = 5.10 Years (approx.)

(ii) Effect of increase in YTM on duration of the Bond:
The calculations are similar to first part except changes in Present value factors.

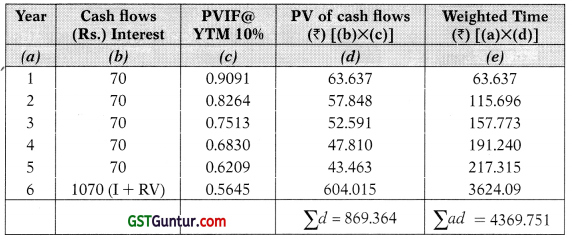
Duration = \(\frac{\text { Weighted Time }}{\text { Purchase Price }}=\frac{\sum a d}{\sum d}=\frac{\text { Rs. } 4369.751}{\text { Rs. } 869.364}\) = 5.025 Years

Alternative Method for determination of Duration:

Formula method	Where
Duration = \( \frac{1+y}{y}-\frac{(1+y)+\operatorname{Period}(c-y)}{c\left[(1+y)^{\text {Period }}-1\right]+y} \)	y = Yield to maturity c = Coupon rate

Duration = \(\frac{1+0.1}{0.1}-\frac{(1+0.1)+6(0.07-0.1)}{0.07\left[(1+0.1)^6-1\right]+0.1}\)
= \(\frac{1.1}{0.1}-\frac{.92}{0.154}\)
= 11 – 5.975 = 5.025 Years (approx.)
The duration of bond decreases, reason being the receipt of slightly higher portion of one’s investment on the same intervals as the present value or purchase price is less.

Question 11.
Mr. A will need ₹ 1,00,000 after two years for which he wants to make one time necessary investment now. He has a choice of two types of bonds. Their details are as below:

	Bond X	Bond Y
Face value	₹ 1,000	₹ 1,000
Coupon	7% payable annually	8% payable annually
Years to maturity	1	4
Current price	₹ 972.73	₹ 936.52
Current yield	10%	10%

Advice Mr. A whether he should invest all his money in one type of bond or he should buy both the bonds and, if so, in which quantity?
Assume that there will not be any call risk or default risk. [Nov. 2015] [6 Marks]
Answer:
Step 1: Determination of duration of the bonds available for investment.
Duration of the bond X:
Since the year to maturity of Bond X is one year, therefore all the cash flows will be at the end of 1st year only. Hence, the duration will be 1 year.

Duration of the bond Y:

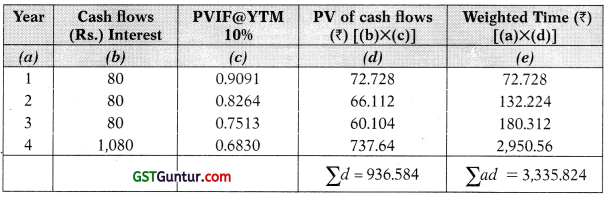
Duration = \(\frac{\text { Weighted Time }}{\text { Purchase Price }}=\frac{\sum a d}{\sum d}=\frac{\text { Rs. } 3,335.824}{\text { Rs. } 936.584}\) = 3.5617 Years

Step 2 : Determination of investment to be made today to meet obligation after 2 years:
= Amount of obligation × PVIF_{(10% 2)}
= Rs. 1,00,000 × 0.8264
= Rs. 82,640

Step 3 : Determination of proportion of investment in Bond X & Bond Y
The duration of both the bonds is different and the duration of liabilities is 2 years. Our objective is to match the duration of the liability with the duration of investment in bonds. Therefore, the weighted average of duration of bonds should be equal to 2 years.
Let x₁ be the investment in Bond X and therefore investment in Bond Y shall be (1 – x₁). The proportion of investment in these two bonds shall be computed as follows:
Required duration= [x₁ × Duration of Bond X] + [(1 – x₁) × Duration of Bond Y]
2 = x₁(1) + (1 – x₁) 3.5617
x₁ = 0.6096 = 61% (appx.)
Therefore, 61 % investment should be made in Bond X and balance 39% in Bond Y.

Step 4 : Investments in Bond X and Bond Y

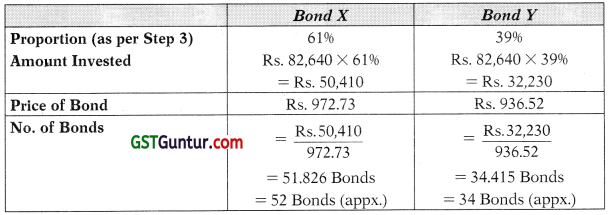
Mr. A must invest in both the bonds in above manner and remain invested for 2 years. Since the duration of Bond X is one year, therefore he should reinvest at the end of first year.

Question 12.
The following data are available for three bonds A, B and C. These bonds are used by a bond portfolio manager to fund an outflow scheduled in 6 years. Current yield is 9%. All bonds have face value of Rs. 100 each and will be redeemed at par. Interest is payable annually.

Bond	Maturity (years)	Coupon rate
A	10	10%
B	8	11%
C	5	9%

(i) Calculate the duration of each bond.
(ii) The bond portfolio manager has been asked to keep 45% of the portfolio money in Bond A. Calculate the percentage amount to be invested in bonds B and C that need to be purchased to immunize the portfolio.
(iii) After the portfolio has been formulated, an interest rate change occurs, increasing the yield to 11%. The new duration of these bonds are: Bond A = 7.15 years, Bond B = 6.03 years and Bond C= 4.27 years.
Is the portfolio still immunized? Why or why not?
(iv) Determine the new percentage of B and C that are needed to immunize the portfolio. Bond A remaining at 45% of the portfolio.
Present values be used as follows: [Nov. 2018] [12 Marks]

Answer:
(i) Determination of duration of the bonds available for investment.
(a) Bond A:

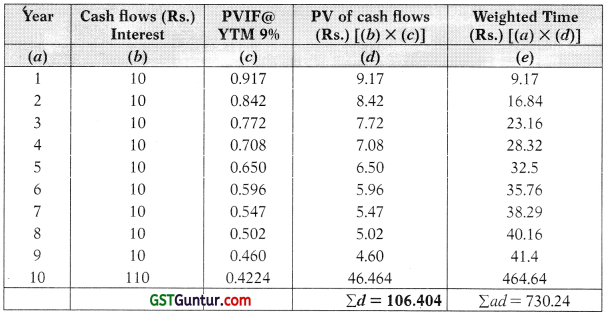
Duration = \(\frac{\text { Weighted Time }}{\text { Purchase Price }}=\frac{\sum a d}{\sum d}=\frac{\mathbf{R s . 7 3 6 0 . 2 4}}{\text { Rs.106.404 }}\) = 6.863 Years

(b) Bond B:

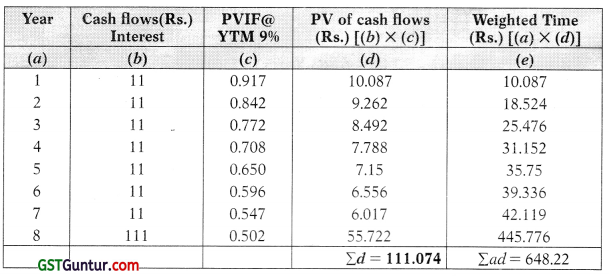
Duration = \(\frac{\text { Weighted Time }}{\text { Purchase Price }}=\frac{\sum a d}{\sum d}=\frac{\text { Rs. } \mathbf{6 4 8 . 2 2}}{\text { Rs. } \mathbf{1 1 1 . 0 7 4}}\) = 5.8359 Years

(c) Bond C:

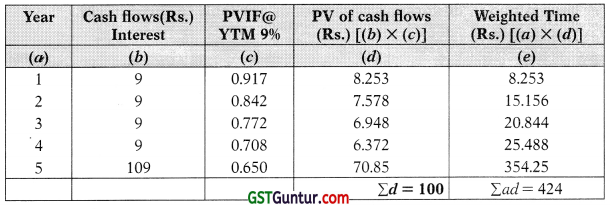
Duration = \(\frac{\text { Weighted Time }}{\text { Purchase Price }}=\frac{\sum a d}{\sum d}=\frac{\mathrm{R s . 4 2 4}}{\mathrm{R s . 1 0 0}}\) = 4.24 Years (approx.)

Formula method	Where
Duration = \( \frac{1+y}{y}-\frac{(1+y)+\text { Period }(c-y)}{c\left[(1+y)^{\text {Periad }}-1\right]+y} \)	y = Yield to maturity c = Coupon rate

(ii) Determination of proportion of investment in Bond B & Bond C given that 45% is invested in Bond A
The duration of the bonds is different and the duration of liabilities is 6 years. Our objective is to match the duration of the liability with the duration of investment in bonds. Therefore, the weighted average of duration of bonds should be equal to 6 years.
Let x₁ be the investment in Bond B and therefore investment in Bond C shall be (1 – 0.45 – x₁) as 45% is invested in Bond A. The proportion of investment in these two bonds shall be computed as follows:

Required duration
= [0.45 × Duration of Bond A]+ [x₁ x Duration of BondB] + [(0.55 – x₁) × Duration of Bond C] = 6
0.45 × 6.863 + x₁(5.8354)+ (0.55 – x₁) 4.24 = 6
3.08835 + 5.8354x₁ + 2.332 – 4.24x₁ = 6
5.42035 + 1.5954 x₁ = 6
1.5954 x₁ =0.57965
x₁ = 0.3633 = 36% (approx.)

Therefore, 45% investment should be made in Bond A, 36% investment should be made in Bond B and balance 19% in Bond C.
Weighted Duration = W_A (D_A) + W_B (D_B) + W_C (D_C)
= 0.45(6.863) + 0.36(5.8354) + 0.19(4.24)
= 6 Yrs. App.

(iii) Weighted Duration of the portfolio, if the Yield changes to 11% and the new duration of the three Bonds are given as under:

Bond	Duration
A	7.15
B	6.03
C	4.27

Weighted Duration = W_A (D_A) + W_B (D_B) + W_C (D_C )
= 0.45(7.15) + 0.36(6.03) + 0.19(4.27)
= 6.1996
The Liability is not immunized as the duration of Bond A with highest maturity and highest weight has increased thereby increasing the duration of the portfolio and since it is slightly beyond 6 years the liability is not immunized.

(iv) New percentage ofB and C: Let x₁ be the investment in Bond B and there-fore investment in Bond C shall be (1- 0.45 – x₁) as 45% is invested in Bond A. The proportion of investment in these two bonds shall be computed as follows:
Required duration
= [0.45x Duration of Bond A]+ [x₁ × Duration of Bond B] + [(0.55 – x₁) × Duration of Bond C] = 6
= 0.45 × 7.15 + x₁(6.03)+ (0.55 – x₁) 4.27
= 6 3.2175 + 6.03x₁ + 2.3485 – 4.27x₁
= 6 5.566 + 1.76x = 6 1.76x₁ = 0.434
x = 0.2466 = 24.66%
Therefore, 45% investment should be made in Bond A, 24.66% investment should be made in Bond B and balance 30.34% in Bond C.
Weighted Duration = W_A (D_A) + W_B (D_B) + W_C (D_C)
= 0.45(7.15) + 0.2466(6.03) + 0.3034(4.27)
= 6 Yrs.

Question 13.
The following data is available for a bond:

Face value	₹ 1,000
Coupon Rate	11%
Years to Maturity	6
Redemption Value	₹ 1,000
Yield to Maturity	15%

(Round-off your answers to 3 decimals)
Calculate the following in respect of the bond:
(i) Current Market Price.
(ii) Duration of the Bond.
(iii) Volatility of the Bond.
(iv) Expected market price if increase in required yield is by 100 basis points,
(v) Expected market price if decrease in required yield is by 75 basis points. [Nov. 2015] [5 Marks]
Answer:
(i) Current Market Price = \(\frac{\text { Coupon Interest }}{\text { Yield } \%}\)
= \(\frac{110}{15 \%}\)
= ₹ 733.33

(ii) Determination of Duration of the Bond:
The following steps are to be taken:
Step 1 Calculation of YTM (Yield to maturity).
It is given in the question as 1596
Step 2 Calculation of Duration.
The duration of a bond is the weighted average of the time it takes to return the investor’s money. The present values of cash flows are to be taken as weights (w).

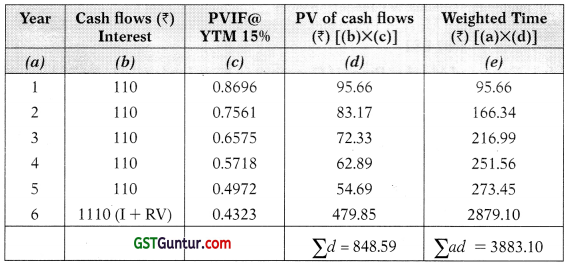
Duration = \(\frac{\text { Weighted Time }}{\text { Purchase Price }}=\frac{\sum a d}{\sum d}=\frac{\text { Rs. } 3883.10}{\text { Rs. } 848.59}\)4.576 Yrs.
Alternative Method for determination of Duration:

Formula method	Where,
Duration = \( \frac{1+y}{y}=\frac{(1+y)+\text { Period }(c-y)}{c\left[(1+y)^{\text {Period }}-1\right]+y} \)	y = Yield to maturity c = Coupon rate

Duration = \(\frac{1+0.15}{0.15}-\frac{(1+0.15)+6(0.11-0.15)}{0.11\left[(1+0.15)^6-1\right]+0.15}\)
= \(\frac{1.15}{0.15}-\frac{0.91}{02944}\)
= 7.6667 – 3.091 = 4.576 Years (approx.)

(iii) Volatility of the Bond

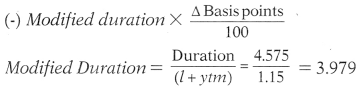
The negative sign indicates that the price will be inversely related to the change in interest rates and the number 3.979 indicates the magnitude of the sensitivity. This means that for every 100 basis points i.e. 1% rise in interest rates the price of the bond will fall approximately by 3.979% and vice versa.

(iv) Expected Market price if increase in requiredyield is by 100 basis points
= (-) 3.979 × \(\frac{100}{100}\) = -3.979%
848. 59 × 3.979% = ₹ 33.77
= Then Market Price will fall by Rs. 33.77 and it will be = 848.59 – 33.77
= ₹ 814.82

(v) Expected Market Price if Decrease in requiredyield is by 75 basis points
(-) 3.979 × \(\frac{100}{100}\) = 2.984%
= 848.59 × 2.984% = 25.32
= Therefore Market Price will rise by Rs. 25.32 and it will be = 848.59 + 25.32 = ? 873.91

Question 14.
XL Ispat Ltd. has made an issue of 14 per cent non-convertible debentures on January 1, 2007. These debentures have a face value of ? 100 and is currently traded in the market at a price of ₹ 90.
Interest on these NCD will be paid through post-dated cheques dated June 30 and December 31. Interest payments for the first 3 years will be paid in advance though post-dated cheques while for the last 2 years, post-dated cheques will be issued at the third year. The bond is redeemable at par on December 31, 2011 at the end of 5 years.
Required:
(i) Estimated the current yield at the YTM of the bond.
(ii) Calculate the duration of the NCD.
(iii) Assuming that intermediate coupon payments are, not available for reinvestment calculate the realized yield on the NCD. [Nov. 2008] [6 Marks]
Answer:
(i) Current yield:
= (Coupon Interest/Market Price) × 100= (14/90) × 100 = 15.55%

(ii) Determination of Duration of the Bond:
The following steps are to be taken:
Step 1: Calculation of YTM (Yield to maturity).
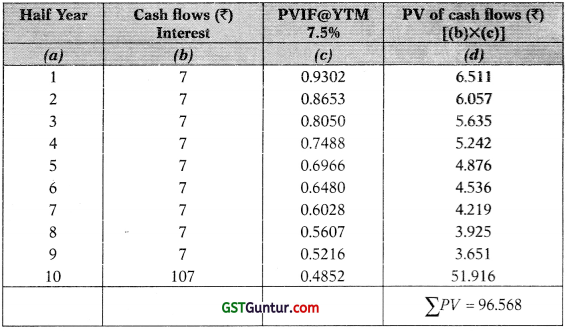
YTM in this case shall be calculated by interpolation. Since, the coupon rate is 1% half yearly and bond is redeemable at par, and the price of the bond is Rs. 90 i.e. the bond is selling below par therefore the YTM will be more than 1% half yearly and as per the current yield also it is 15.55% p.a so the first trial is assumed at 7.5%.
Half yearly Interest (I) = Rs. 100 × = Rs. 7
Redemption Value (RV) = Rs. 100
Maturity Period (n)= 5 Years =10 half years

Accordingly, Present value of future inflows can be calculated as
= ₹ 7 (PVIFA_{(7.5%, 10)}) + ₹ 100 × PVIF_(7.5%,10)
= ₹ 7 × 6.8641 + ₹ 100 × 0. 4852
= ₹ 48.0487 + 48.52
= ₹ 96.568

Alternative Method

Since the present value is required to be brought down, the next trial should be at higher rate of interest. Taking 9%, the present value will be:
= ₹ 7 × PVIFA_{(9% 10)} + ₹ 100 × PVIF_{(9% 10)}
= ₹ 7 × 6.418 + ₹ 100 × 0.4224
= ₹ 44.93 + 42.24
= ₹ 87.17

Calculation of Yield to Maturity (YTM):

Yield	Value (Rs.)
7.5%	96.57
9uo	87.17

YTM at Rs. 90 can be calculated using interpolation as pei the manner given below
By interpolation, the YTM is
= 7.5% + \(\frac{96.57-90}{96.57-87.17}\) × (9% – 7.5%)
= 7.5% + \(\frac{6.57}{9.4}\) × (1.5%)
= 8.548% semi annual
Therefore, annualized ytm = 8.548% × 2=17.10% app.

Step 2: Calculation of Duration.
The duration of a bond is the weighted average of the time it takes to return the investor’s money. The present values of cash flows are to be taken as weights (w).

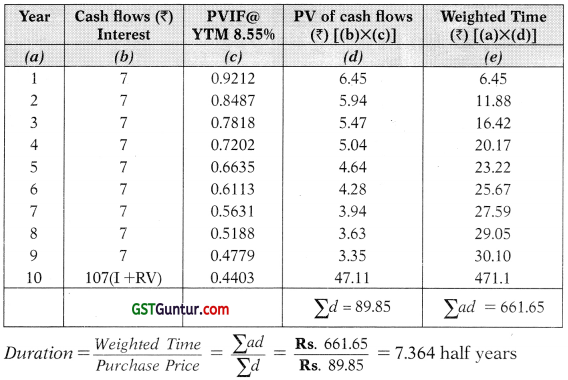
= 3.682 yrs.

Alternative Method for determination of Duration:

Formula Method	Where,
Duration = \( \frac{1+y}{y}-\frac{(1+y)+\text { Period }(c-y)}{c\left[(1+y)^{\text {Period }}-1\right]+y} \)	Y = Yelid to maturity c = Coupon rate

Duration = \(\frac{1+0.0855}{0.0855}-\frac{(1+0.0855)+10(0.07-0.0855)}{0.07\left[(1+0.0855)^{10}-1\right]+0.0855}\)
= \(\frac{1.0855}{0.0855}-\frac{0.9305}{0.1745}\)
= 12.696 – 5.332= 7.364 half Years (approx.) = \(\frac{7.364}{2}\) = 3.682 year

(i) If the interest received is not reinvested then realized yield can be calcu-lated as follows:
Half yearly Interest (I) = Rs. 100 × \(\frac{7}{100}\) = Rs. 7

(ii) Redemption Value (RV) = Rs. 100

(iii) Maturity Period (n) = 5 Years =10 half years

(iv) Total amount from interest = 7 × 10 = Rs. 70
Total realized Value = Rs. 170
Realized Yield. 170 = 90 (1 + r)5
Solving for r:
r = 13.5696

Question 15.
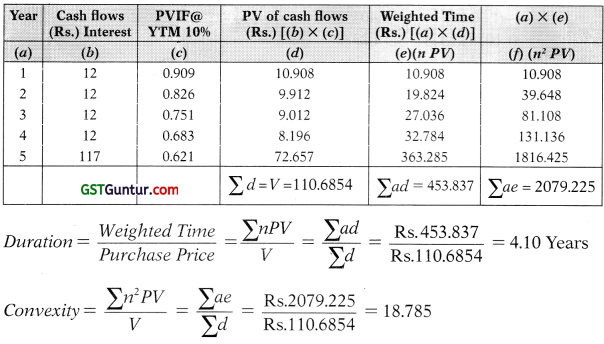
The Nominal value of 12% bonds issued by a company is Rs.100. The bonds are redeemable at Rs. 105 at the end of year 5. Coupons are paid annually.
Determine the duration and convexity of the bond at required annual yield rate of 10%. [Practice question]
Answer:
(i) Determination of duration and convexity of the bond:

Question 16.
The following is the yield structure of AAA rated debenture:
Period-Yield (%)
3 months-8.5%.
6 months-9.25
1 year-10.50
2 years-11.25
3 years and above-12.00
(i) Based on the expectation theory calculate the implicit one-year forward rates in year 2 and year 3.
(ii) If the interest rate increases by 50 basis points, w hat will be the percentage change in the price of the bond having a maturity of 5 years? Assume that the bond is fairly priced at the moment at ₹ 1,000. [Nov. 2008] [4 Marks]
Answer:
(i) Implicit 1 year forward rates for year 2 and year 3

(ii) If fairly priced at ₹ 1,000 and rate of interest increases to 12.596, the percentage change will be as follows:

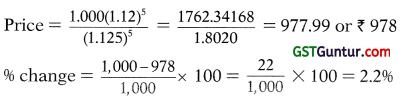
Question 17.
Consider the following data for Government Securities:

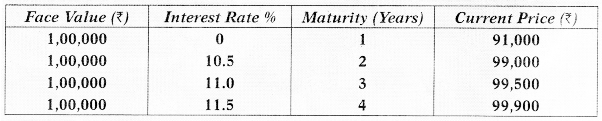
Calculate the forward interest rates. [May 2010] [8 Marks]
Answer:
To get forward interest rates,
(i) For 1 year, the one year Government Security.
₹ 91,000 = ₹ 1,00,000/(1 + r)
r = 0.099
r = 9.9%

(ii) The two years Government Security
₹ 99,000 = (₹ 10,500/1.099) + (₹ 1,10,500/(1.099) (1+r))
r = 0.124
r = 12.4%

(iii) The three years Government Security
₹ 99,500 = (11,000/1.099) + [(₹ 11,000/1.099) (1.124)] + [(₹ 1,11,000/1.099) (1.124(1 +r)]
r = 0.115
r = 11.5%

(iv) The four years Government Security
₹ 99,000 = (₹ 11,500/1.099) + [(₹ 11,500/1.099) (1.124)] + [(₹? 11,500/1.099) (1.124) (1.115)] + [(₹ 1,11,500/1.099) (1.124) (1.115) (1 + r)]
r = 0.128
r = 12.8%

Question 18.
Sonic Ltd. issued 8% 5 year bonds of Rs. 1,000 each having a maturity of 3 year. The present rate of interest is 12% for one year tenure. It is expected that forward rate of interest for one year tenure is going to fall by 75 basis points and further by 50 basis points for next year. This bond has a beta value of 1.02 and is more popular in the market due to less credit risk.
Calculate:
(i) Intrinsic value of bond.
(ii) Expected price of bond in the market. [Nov. 2013] [Nov. 2018 old syllabus] [5 Marks]
Answer:
The following information is available :

Face Value	1000
Coupon rate	8%
Remaining Life	3 Years
Present rate of Interest	12%
Forward rate after one year	11.25% (12 – 0.75)
Forward rate after 2 years	10.75% (11.25 – 0.50)
Beta	1.02

(i) Intrinsic Value of the Bond:

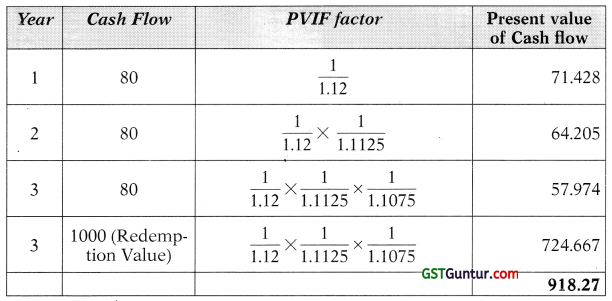
The intrinsic value of the Bond is Rs. 918.27

(ii) Expected Price of the Bond:
= Intrinsic value × Beta
= 918.27 × 1.02
= Rs. 936.64

Question 19.
Sabanam Ltd. has issued convertible debenture with coupon rate 11%. Each debenture has an option to convert to 16 equity shares at any time until the date of maturity. Debentures will be redeemed at Rs.100 on maturity after 5 years. An investor generally requires a rate of return of 8% p.a. on a 5 year security. As an advisor, when will you advise the investor to exercise conversion for given market prices of the equity share of (i) Rs. 5 (ii) Rs. 6 and (iii) Rs. 7.10. [May 2018 New syllabus] [8 Marks]

Cumulative PV factor for 8% for 5 year	3.993
P.V factor for 8% for year 5	0.681

Answer:
The value of Debentures if conversion option is not exercised:
Artnual Interest (I) = Rs. 100 × \(\frac{11}{100}\) = Rs. 11
Redemption Value (RV) = Rs. 100
Maturity Period (n) = 5 Years

Accordingly, Present value of future inflows can be calculated as
= Rs. 11 PVIFA_(8%5) + Rs. 100 PVIF_{(8% 5)}
= Rs. 11 3.993 + Rs. 100 0.681
= Rs. 43.923 + 68.10
= Rs. 112.023

The value of Shares if conversion option is exercised at various prices:

S. No.	If the price of the share is	Com ersion Value
(i)	R.s. 5	Rs. 80 (5 × 16)
(ii)	Rs. 6	Rs. 96 (6 × 16)
(iii)	Rs. 7.10	Rs. 113.60(7.1 × 16)

Conclusion: Conversion value is more than straight value of the bond only at the price of Rs. 7.10, therefore the conversion option is exercisable only if the share price is Rs. 7.10.

Question 20.
Pineapple Ltd. has Issued fully convertible 12 per cent debentures of ₹ 5,000 face value, convertible into 10 equity shares. The current market price of the debentures is ₹ 5,400. The present market price of equity shares is ₹ 430.
Calculate:
(i) The conversion value [3 Marks]
(ii) The conversion percentage premium [Nov. 2011] [3 Marks]
Answer:The following information is given in the question:
Face Value of the Debenture : Rs. 5,000
Coupon Rate : 12%
Conversion Ratio: 10 Equity Shares for 1 Debenture
Market Price of the Debenture Rs. 5,400
Market Price of Equity Share Rs. 430

(i) Calculation of Conversion Value per Debenture:
Conversion Value of Debenture = Value of Shares received per debenture
= Market Price per share × Conversion Ratio
= 430 × 10
= Rs. 4,300

(ii) Calculation of Conversion Percentage premium:
Market Conversion Price = \(\frac{\text { Market Price of the Debenture }}{\text { Conversion Ratio }}\)
= \(\frac{R s .5,400}{10}\) = Rs. 540

Conversion Premium per Share = Market Conversion Price – Market Price per Share
= Rs. 540 – Rs. 430
= Rs. 110

Conversion Premium per Share = \(\frac{\text { Conversion Premium per Share }}{\text { Market Price per Share }}\)
= \(\frac{R s .110}{430}\) × 100
= 25.58%

Question 21.
The data given below relates to a convertible bond:

Face Value	₹ 250
Coupon rates	12%
No. of shares per bond	20
Market price of share	₹ 12
Straight value of bond	₹ 235
Market price of convertible bond	₹265

Calculate:
(i) Stock value of bond.
(ii) The percentage of downside risk.
(iii) The conversion premium
(iv) The conversion parity price of the stock. [Nov. 2008] [8 Marks]
Answer:
The following information is given in the question:
Face Value of the Bond : Rs. 250
Coupon Rate : 12%
Conversion Ratio : 20
Equity Shares for 1 Bond
Market Price of the Convertible Bond : Rs. 265
Market Price of Equity Share : Rs. 12
Straight Value of Bond : Rs. 235
(i) Calculation of Stock Value or Conversion Value of Bond:
Conversion Value of Bond = Value of Shares received per Bond
= Market Price per share × Conversion Ratio
= 12 × 20 = Rs. 240

(ii) Percentage of Down side Risk
Market Price of the Bond = \(\frac{\text { Market Price of the Bond-Straight Value of the Bond }}{\text { Straight Value of the Bond }} \) × 100
= \(\frac{R s .265-235}{235}\) × 100
= 12.77%

(iii) Calculation of Conversion Percentage premium:
Market Conversion Price = \(=\frac{\text { Market Price of the Bond }}{\text { Conversion Ratio }}\) × 100
= \(\frac{R s .265}{20}\) = Rs. 13.25

Conversion Premium per Share = Market Conversion Price – Market Price per Share
= Rs. 13.25 – Rs. 12
= Rs. 1.25

Conversion Percentage Premium = \(\frac{\text { Conversion Premium per Share }}{\text { Market Price per Share }}\)
= \(\frac{R s .1 .25}{12}\) × 100
= 10.42%

(iv) The Conversion Parity Price Or the Market Conversion Price
Market Conversion Price = \(\frac{\text { Market Price of the Bond }}{\text { Conversion Ratio }}\)
= \(\frac{R s .265}{20}\) = Rs. 13.25

Question 22.
The following is the data related to 9% fully convertible (into equity shares) debentures issued by Delta Ltd. at Rs.1000

Market price of 9% Debenture Rs.	1,000
Conversion Ratio (No. of shares)	25
Straight value of 9% Debentures	800
Market price of Equity share on the date of conversion Rs.	30
Expected Dividend per share Rs.	1

Calculate:
(а) Conversion value of Debenture;
(b) Market conversion Price;
(c) Conversion premium per share;
(d) Ratio of conversion premium;
(e) Premium over straight value of Debenture;
(f) Favourable income differential per share and
(g) Premium pay back period
Answer:
The following information is given in the question:

Face Value of the Debenture : Rs. 1,000
Market price of the debenture : Rs. 1,000
Coupon Rate : 9%
Conversion Ratio : 25 Equity Shares for 1 debenture
Expected dividend per share : Re. 1
Market Price of Equity Share : Rs. 30
Straight Value of 9% debenture : Rs. 800

(a) Calculation of Stock Value or Conversion Value of Debenture:
Market Price of one equity share × Conversion ratio = 30 × 25
= Rs. 750.

(b) Market Price of the debenture = \(\frac{\text { Market Price of the debenture }}{\text { Conversion Ratio }}\)
= \(\frac{\text { Rs. } 1000}{25}\) = Rs. 40

(c) Calculation of Conversion premium:
Conversion Premium per Share = Market Conversion Price – Market Price per Share
= Rs. 40 – Rs. 30
= Rs. 10

(d) Ratio of conversion Premium
\(\frac{\text { Premium per share }}{\text { Price of the share }} \) × 100
= \(\frac{\text { Rs. } 10}{30}\) × 100
= 33.33%

(e) Premium over straight value of debenture
Market Conversion Price of the Share- Straight Price of the share based on straight value of bond i.e. Rs. 800/25 = 32
= Rs. 8 per share
= \(\frac{\text { Rs. } 8}{32}\) × 100 = 25%
Or
\(\frac{\text { Market Price of the debenture }}{\text { Straight value of debenture }}\) – 1 = (\(\frac{R s .1000}{800}\) – 1) × 100 = 25%

(f) Favourable income differential per Share:
\(\frac{\text { Coupon interest from debenture }- \text { Conversion ratio } \times \text { Expected dividend per share }}{\text { Conversion ratio }}\) × 100
= \(\frac{90-25 \times 1}{25}\) = Rs. 2.6

(g) Premium pay back period
\(\frac{\text { Conversion premium per share }}{\text { Favourable income differential per share }}=\frac{\text { Rs.10 }}{\text { Rs.2.6 }}\) = 3.846 years

Question 23.
The following is the data related to 8.5% fully convertible (into equity shares) debentures issued by JAC Ltd. at Rs.1000

Market price of 9% Debenture Rs.	900
Conversion Ratio (No. of shares)	30
Straight value of 9% Debentures	700
Market price of Equity share on the date of conversion Rs.	25
Expected Dividend per share Re.	2

Calculated:
(a) Conversion value of Debenture;
(b) Market conversion Price;
(c) Conversion premium per share;
(d) Ratio of conversion premium;
(e) Premium over straight value of Debenture
(f) Favourable income differential per share; and
(g) Premium pay back period [Mock Test August 2018] [8 Marks]
Answer:
The following information is given in the question:
Face Value of the Debenture : Rs. 1,000
Market price of the debenture : Rs. 900
Coupon Rate Conversion Ratio : 8.5%
Expected dividend per share : 30
Equity Shares for 1 debenture : Re. 1
Market Price of Equity Share : Rs. 25
Straight Value of 9% debenture : Rs. 700
(a) Calculation of Stock Value or Conversion Value of Debenture:
Market Price of one equity share × Conversion ratio = 25 × 30 = Rs. 750.

(b) Market Conversion Price = \(\frac{\text { Market Price of the debenture }}{\text { Conversion Ratio }}\)
= \(\frac{\text { Rs. } 900}{30}\) = Rs. 30

(c) Calculation of Conversion premium:
Conversion Premium per Share = Market Conversion Price – Market Price per Share
= Rs. 30 – Rs. 25 = Rs. 5

(d) Ratio of conversion Premium
\(\frac{\text { Premium per share }}{\text { Price of the share }}\) × 100 = \(\frac{\text { Rs. } 5}{25}\) × 100 = 20%

(e) Premium over straight value of debenture
Market Conversion Price of the Share – Straight Price of the share based on straight value of bond i.e. Rs. 700/30 = 23.33
Rs. 30 – Rs. 23.33 = Rs. 6.67 per share
= \(\frac{R s .6 .67}{23.33}\) × 100 = 28.60% approx.

Or \(\frac{\text { Market Price of the debenture }}{\text { Straight value of debenture }}\) – 1 = [\(\frac{R s .900}{700}\) – 1] × 100 = 28.57%

(f) Favourable income differential per share:
\(\frac{\text { Coupon interest from debenture }- \text { Conversion ratio } \times \text { Expected dividend per share }}{\text { Conversion ratio }}\) × 100

(g) Premium pay back period
\(\frac{\text { Conversion premium per share }}{\text { Favourable income differential per share }}=\frac{\text { Rs. } 5}{\text { Rs. } 1.833}\) = 2.73 vears

Question 24.
GUI Ltd., AAA rated company has issued fully convertible bonds on the following terms, a year ago:
Face value of bond : ₹ 1,000
Coupon (interest rate) : 8.5%
Time to Maturity (remaining) : 3 years
Interest Payment : Annual at the end of year
Principal Repayment : At the end of bond maturity
Conversion ratio (No. of shares per bond) : 25
Current market price per share : ₹ 45
Market price of convertible bond : ₹ 1, 175
AAA rated company can issue plain vanilla bonds without corn ersion option at an interest rate of 9.5%.
Required:
Calculate as of today:
(i) Straight Value of bond.
(ii) Conversion Value of the bond.
(iii) Conversion Premium.
(iv) Percentage of downside risk,
(v) Conversion Parity Price.

[May 2014] [4 + 1 + 1 + 1 + 1 = 8 Marks]
Answer:
The following information is given in the question:
Face Value of the Bond : Rs. 1, 000
Coupon Rate : 85%
Conversion Ratio : 25 Equity Shares for 1 bond
Market Price of the Convertible : Rs. 1, 175
Bond Market Price of Equity Share : Rs. 45
Remaining life of Bond ie. Maturity : 3yrs
Interest payments : Anuual
Redemption at maturity : At par
This question is different from previous as the straight value of Bond is required to be calculated and therefore maturity period and redemption price is also given in the question.
(i) Calculation of Straight Value of Bond
The present value of future inflows (comprising both interest as well as redemption value) discounted at 9.5% is the straight value of the Bond.
Annual Interest (I) = Rs. 1000 × \(\frac{8.5}{100}\) = Rs. 85
Redemption Value (RV) = Rs. 1000
Maturity Period (n) = 3 Years

Accordingly, Present value of future inflows can be calculated as
= ₹ 85 × PVIFA (9.5%,3) + ₹ 1000 × PVIF (9.5%,3)
= ₹ 85 × 2.5089 + ₹ 1000 × 0.7617
= ₹ 213.26 + 761.7 = ₹ 974.96

(ii) Calculation of Stock Value or Conversion Value of Bond:
Conversion Value of Bond = Value of Shares received per Bond
= Market Price per share × Conversion Ratio
= 25 × 45
= Rs. 1125

(iii) Calculation of Conversion premium:
Market Conversion Price = \(\frac{\text { Market Price of the Bond }}{\text { Conversion Ratio }}\)
= \(\frac{\mathrm{Rs} .1175}{25}\) = Rs. 47

Conversion Premium per Share = Market Conversion Price – Market Price per Share
= Rs. 47 – Rs. 45
= Rs. 2

(iv) Percentage of Down side Risk
\(\frac{\text { Market Price of the Bond }- \text { Straight Value of the Bond }}{\text { Straight Value of the Bond }}\) × 100
= \(\frac{\text { Rs. } 1175-974.96}{974.96}\) × 100 = 20.52%

(v) The Conversion Parity Price or the Market Conversion Price
Market Conversion Price = \(\frac{\text { Market Price of the Bond }}{\text { Conversion Ratio }}\)
= \(\frac{\text { Rs. } 1175}{25}\) = Rs. 47

Question 25.
A Ltd. has issued convertible bonds, which carries a coupon rate of 14%. Each bond is convertible into 20 equity shares of the company A Ltd. The prevailing interest rate for similar credit rating bond is 8%. The convertible bond has 5 years maturity. It is redeemable at part at ? 100.

You are required to estimate:
(Calculations be made up-to 3 decimal places)
(i) current market price of the bond, assuming it being equal to its funda-mental value;
(ii) Minimum market price of equity share at which bond holder should exercise conversion option; and
(iii) duration of the bond.
Answer:
The following information is given in the question:
Face Value of the Bond : Rs. 100
Coupon Rate : 14%
Conversion Ratio : 20 Equity Shares for 1 Bond
Remaining life of Bond i.e. Maturity : 5 yrs.
Interest payments : Annual
Redemption at maturity : At Par

(i) Calculation of Current Market Price or the Straight Value of Bond
The present value of future inflows (comprising both interest as well as redemption value; discounted at 8% is the market price or the straight value of the Bond.
Annual Interest (I) = Rs. 100 × \(\frac{14}{100}\) = Rs. 14
Redemption Value (RV) = Rs. 100
Maturity Period (n) = 5 Years
Accordingly, Present value of future inflows can be calculated as
= ₹ 14 × PVIFA (896,5) + ₹ 1000 × PVIF (8%,5)
= ₹ 14 × 3.993 + ₹ 100 × 0.681
= ₹ 55.902 + 68.1
= ₹ 124.002 = Rs. 124 (Approx.)

Alternatively:
Current Market Price of Bond

₹ 124

(ii) Minimum Price at which Bond holder should exercise Conversion:
It should be the Market conversion price which is calculated as below:
\(\frac{\text { Market Price of the Bond }}{\text { Conversion ratio }}=\frac{124.002}{20 \text { shares }}\) = ₹ 6.20 Per Share

(iii) Duration of Bond (Formula method)
Formula method
Duration = \(\frac{1+y}{y}-\frac{(1+y)+\text { Period }(c-y)}{c\left[(1+y)^{\text {Period }}-1\right]+y}\)

Where,
y = Yield to maturity
c = Coupon rate

Duration = \(\frac{1+0.08}{0.08}-\frac{(1+0.08)+5(0.14-0.08)}{0.14\left[(1+0.08)^5-1\right]+0.08}\)
= \(\frac{1.08}{0.08}-\frac{1.38}{0.1457}\)
= 13.5 – 9.472 = 4.028 Years (approx)

Question 26.
XYZ company has current earnings of 13 per share with 5,00,000 shares outstanding. The company plans to issue 40,000, 7% convertible preference shares of ₹ 50 each at par. The preference shares are convertible into 2 shares for each preference shares held. The equity share has a current market price of ₹ 21 per share.
(i) What is preference shares’ conversion value?
(ii) What is conversion premium?
(iii) Assuming that total earnings remain the same, calculate the effect of the Issue on the basic earning per share (a) before conversion (b) after conversion.
(iv) If profits after tax increases by ₹ 1 million what will be the basic EPS
(a) before conversion and (b) on a fully diluted basis? [Nov. 2009] [8 Marks]
Answer:
The following information is given in the question:
Face Value of the Share : Rs. 50 1%
Rate of Preference Share : 7%
Conversion Ratio : 2 Equity Shares for 1 Preference Share
Market Price of the Preference Share : Rs. 50
Market Price of Equity Share : Rs. 21
No. of Equity Shares Outstanding : 5,0, 000
EPS : Rs. 3 per Share
Total number of convertible preference shares to be issued : 40,000

(i) Calculation of Conversion Value of Preference Shares:
Conversion Value of Pref. Share = Value of equity Shares received per Pref. Share
= Market Price per Equity share × Conversion Ratio
= Rs. 21 × 2 = Rs. 42

(it) Calculation of Conversion Percentage premiunv
Market Conversion Price = \(\frac{\text { Market Price of the Pref. Share }}{\text { Conversion Ratio }}\)
= \(\frac{R s .50}{2}\) = Rs. 25
Conversion Premium per Share = Market Conversion Price – Market Price per Share
= Rs. 25 – Rs. 21 = Rs. 4
Conversion Percentage Permium = \(\frac{\text { Conversion Premium per Share }}{\text { Market Price per Share }}\)
= \(\frac{R s .4}{21}\) × 100
= 19.05%

(iii) Statement of EPS before Conversion

Particulars	Amount (₹)
Total earning [3 × 5,00,000]	15,00,000
(-) Preference dividend (40,000 × 50 × 1%)	(1,40,000)
Earnings for Equity Shareholders	13,60,000
No. of Equity Shares	5,00,000
EPS	2.72

Statement of EPS After Conversion

Particulars	Amount (₹)
Total earning No. of Equity shares [5,00,000 + (40,000 × 2)]	15,00,000 5,80,000
EPS	2.586

(iv) If Profits increase by 10 Lakhs
Statement of EPS before Conversion

Particulars	Amount (₹)
Total earning [(3 × 5,00,000) + 10,00,000] (-) Preference dividend Earnings for Equity Shareholder No. of Equity Shares	25,00,000 (1,40,000)
	23,60,000 5,00,000
EPS	4.72

Statement of EPS after Conversion

Particulars	Amount (₹)
Total earning No. of Equity Shares [5,00,000 + (40,000 × 2)]	25,00,000 5,80,000
EPS	4.31

Question 27.
P Ltd. has current earnings of ₹ 6 per share with 10,00,000 shares outstanding. The company plans to issue 80,000,8% convertible preference shares of ₹ 100 each at par. The preference shares are convertible into 2 equity shares for each preference share held. The equity share has a current market price of ₹ 42 per share. Calculate:
(i) What is preference share’s conversion value?
(ii) What is conversion premium?
(iii) Assuming that total earnings remain the same, calculate the effect of the issue on the basic earnings per share (A) before conversion (B), after conversion.
(iv) If profits after tax Increases by ₹ 20 Lakhs what will be the basic EPS, (A) before conversion and (B) on a fully diluted basis? [May 2017] [8 Marks]
Answer:
The following information is given in the question:
Face Value of the Share : Rs. 100
Rate of Preference Dividend : 8%
Conversion Ratio : 2 2 Equity Shares for 1 Preference Share
Market Price of the Preference Share : Rs. 100
Market Price of Equity Share : Rs. 42
No. of Equity Shares Outstanding : 10,00,000
EPS : Rs. 6 per shares
Total number of convertible preference shares to be issued : 80,000

(i) Calculation of Conversion Value of Preference Shares:
Conversion Value of Pref. Share = Value of equity Shares received per Pref. Share
= Market Price per Equity share × Conversion Ratio
= Rs. 42 × 2 = Rs. 84

(ii) Calculation of Conversion Percentage premium:
Market Conversion Price = \(\frac{\text { Market Price of the Pref. Share }}{\text { Conversion Ratio }}\)
= \(\frac{\mathrm{Rs} \cdot 100}{2}\) = Rs. 50
Conversion Premium per Share = Market Conversion Price – Market Price per Share
= Rs. 50 – Rs. 42 = Rs. 8
Conversion Premium Premium = \(=\frac{\text { Conversion Premium per Share }}{\text { Market Price per Share }}\)
= \(\frac{\text { Rs. } 8}{42}\) = 19.05%

(iii) Statement of EPS before Conversion

Particulars	Amount (₹)
Total earning [6 X 10,00,0001 (-) Preference dividend (80,000 × 100 × 8%)Earnings for Equity Shareholders No. of Equity Shares	60,00,000 (6,40,000)
	53,60,000 10,00,000
	5.36

Statement of EPS after Conversion

Particulars	Amount (₹)
Total earning No. of Equity shares (10,00,000 + (80,000 × 2)]	60,00,000 11,60,000
EPS	5.17

(iv) If Profits increase by 20 Lakhs
Statement of EPS before Conversion

Particulars	Amount (₹)
Total earning [6 × 10,00,0001 + 20,00,000] (-) Preference dividend (80,000 × 100 × 8%)Earnings for Equity Shareholder No. of Equity Shares	80,00,000 (6,40,000)
	73,63,000 10,00,000
EPS	7.36

Statement of EPS after Conversion

Particulars	Amount (₹)
Total earning No. of Equity Shares [10,00,000 + (80,000 × 2)]	80,00,000 11,60,000
EPS	6.90

Question 28.
ABC Ltd. has ₹ 300 million, 12 per cent bonds outstanding with six years remaining to maturity. Since interest rates are falling, ABC Ltd. is contemplating of refunding these bonds with a ₹ 300 million issue of 6 year bonds carrying a coupon rate of 10 per cent. Issue cost of the new bonds will be ₹ 6 million and the call premium is 4 per cent. ₹ 9 million being the unamortized portion of issue cost of old bonds can be written off no sooner the old bonds are called off. Marginal tax rate of ABC Ltd. is 30 per cent. You are required to analyse the bond refunding decision. [May 2009] [6 Marks]
Answer:
1. Calculation of initial outlay:

	₹ (million)
a. Face value	300
Add: Call premium	12
Cost of calling old bonds	312
b. Gross proceed of new issue	300
Less: Issue costs	6
Net proceeds of new issue	294
c. Tax savings on call premium and unamortized cost 0.30 (12 + 9)	6.3
Initial outlay = ₹ 312 million – ₹ 294 million – ₹ 6.3 million = ₹ 11.7 million	6.3

2. Calculations of net present value of refunding the bond:

Saving in annual interest expenses	7 (million)
[300 × (0.12-0.10)] Less: Tax saving on interest and amortization	6.00
0.30 × [6 + (9 – 6)/6]	1.95
Annual net cash saving	4.05
PVIFA (7% 6 years)	4.766
Present value of net annual cash saving	= ₹ 19.30 million
Less: Initial outlay	= ₹ 11.70 million
Net present value of refunding the bond Decision: The bonds should be refunded.	₹ 7.60 million

Question 29.
M/s. Earth Limited has 11% bond worth of ₹ 2 crores outstanding with 10 years remaining to maturity.
The company is contemplating the issue of a ₹ 2 crores 10 years bond carrying the coupon rate of 9% and use the proceeds to liquidate the old bonds.
The unamortized portion of issue cost on the old bonds is ₹ 3 lakhs which can be written off no sooner the old bonds are called. The company is paying 30% tax and it’s after tax cost of debt is 7%. Should Earth Limited liquidate the old bonds?
You may assume that the issue cost of the new bonds with be ₹ 2.5 lakhs and the call premium is 5%. [May 2013] [6 Marks]
Answer:
1. Computation of initial outlay:

		(₹ lakhs)
(a)	Face value	200.00
	Add: Call premium	10.00
	Cost of calling old bonds	210.00
(b)	Gross proceed of new issue	200.00
	Less: Issue costs	2.50
	Net proceeds of new issue	197.50
(c)	Tax savings on call premium and unamortized costs 0.30 (10 + 3)	3.90 lakhs
	Therefore, Initial outlay = ₹  210 lakhs – ₹  197.50 lakhs – ₹  3.90 lakhs

2. Computation of net present value of refunding the bond:

	₹ lakhs
Saving in annual interest expenses[₹ 200 (0.11 – 0.09)]	4.000
Less: Tax saving on interest and amortization 0.30 [4 + (3 – 2.5)/10]	1.215
Annual net cash saving	2.785
PVIFA (7%, 10 years)	7.024
Present value of net annual cash saving	₹ 19.56 lakhs
Less: Initial outlay	₹ 8.60 lakhs
Net present value of refunding the bond	₹ 10.96 lakhs

Decision, Since the NPV of refunding the bond is favourable, the bonds should be refunded.

Question 30.
Tangent Limited is considering calling Rs. 3 crores of 30 years, Rs. 1000 bond issued 5 years ago with a coupon interest rate of 14 per cent. The bonds have a call price of Rs. 1,150 and had initially collected proceeds of Rs. 2.91 crores since a discount of Rs. 30 per bond was offered. The initial floating cost was Rs. 3,90,000. The company intends to sell Rs. 3 crores of 12 per cent coupon rate, 25 years bonds to raise funds for retiring the old bonds. It proposes to sell the new bonds at their par value of Rs. 1,000. The estimated floatation cost is Rs. 4,25,000. The company is paying 40% tax and its after tax cost of debt is 8 per cent. As the new bonds must first be sold and then their proceeds to be Used to retire the old bonds, the company expects a two months period of overlapping interest during which interest must be paid on both the old and the new bonds. You are required to evaluate the bond retiring decision. [PVIFA_8%,25 = 10.675] [Nov. 2018] [8 Marks]
Answer:
1. Computation of initial outlay:

	(Rs. in lakhs)
(a) Face value	300.00
Add: Call premium	45.00
Cost of calling old bonds	345.00
(b) Gross proceed of new issue	300.00
Less: Issue costs	4.25
Net proceeds of new issue	295.75
(c) Tax savings on call premium and unamortized costs 0.40 (45+10.75)(W.N.)	22.30
(d) Overlapping Interest after tax (300 × 0.14 × \(\frac{2}{12}\)) (1-0.4)	= 4.2
Therefore, Initial outlay = ₹ 345 + 4.2 – (₹ 295.75 + 22.30) 31.15

2. Annual cash flow savings: (Rs. in Lakhs)
(a) Old bond

(i) Interest cost after tax (300 × 0.14)(1 – 0.4)	25.20
(ii) Tax saving on amortization of discount (9,00,000/30) (0.40)	0.12
(iii) Tax saving on amortization of floatation costs (390000/30)(0.40)	0.052
Annual cost	25.028

(b) New bond

(i) Interest cost after tax (300 × 0.12)(1 – 0.4)	21.60
(ii) Tax saving on amortisation of discount	Nil
(iii) Tax saving on amortisation of floatation costs (425000/25 × 0.40)	0.068

Annual cost

Saving in annual expenses Annual net cash saving (25.028 – 21.532)	3.496
PVIFA (8°o, 25 years)	10.675
∴ Present value of net annual cash saving	Rs. 37.31980 lakhs
Less: -Initial outlay	Rs. 31.15 lakhs
Net present value of refunding the bond	Rs. 6.1698 lakhs

Decision Since the NPV of refunding the bond is favourable, the bonds should be refunded.

Working Note:
UnamortizedDiscount and issue costs:

Question 51.
A firm had been paid dividend at ₹ 2 per share last year. The estimated growth of the dividends from the company is estimated to be 5% p.a. Determine the estimated market price of the equity share if the estimated growth rate of dividends (i) rises to 8%, and (ii) falls to 3%. Also find out the present market price of the share, given that the required rate of return of the equity investors is 15.5%. [Nov. 2009] [6 Marks]
Answer:
In this case the company has paid dividend of ₹ 2 per share during the last year.
The growth rate (g) is 5%. Then, the current year dividend (D₁) with the expected growth rate of 5°o will be = D₀( 1+g) = ₹ 2.10.
The share price is P₀ = \(\frac{D_1}{K_e-g}\)
= \(\frac{\text { Rs. } 2.10}{0.155-0.05}\)
= ₹ 20

In case the growth rate rises to 8% then the dividend for the current year. (Dt) would be ₹ 2.16 and market price would be
= \(\frac{R s .2 .16}{0.155-0.08}\)
= ₹ 28.80
In case growth rate falls to 3% then the dividend for the current year (D,) would be ₹ 2.06 and market price would be –
= \(\frac{R s .2 .06}{0.155-0.03}\)
= ₹ 16.48
Conclusion:
The market price of the share is expected to vary in response to change in expected growth rate in dividends.

Question 32.
Shares of Volga Ltd. are being quoted at a price-earnings ratio of 8 times. The company retains 50% of its Earnings per Share. The company’s EPS is Rs. 10.
You are required to determine:
(1) The cost of equity to the company if the market expects a growth rate of 15% p.a.
(2) The indicative market price with the same cost of capital and if the anticipated growth rate is 16% p.a.
(3) The market price per share if the company’s cost of capital is 20% p.a. and the anticipated grow th rate is 18% p.a. [Nov. 2018] [8 Marks]
Answer:
(1) As per Dividend Discount Model approach the firm’s expected or required return on equity is computed as follows:
K_c = \(\frac{\text { Expected dividend at the end of year } 1\left(\mathbf{D}_1\right)}{\text { Current Market Price }\left(\mathbf{P}_0\right)}\) + Expected Growth Rate of Dividend
Current Market Price = P/E ratio × EPS = 8 × 10 = Rs. 80
D0= 50% of EPS and EPS is Rs. 10
Therefore, D0= Rs. 5.0
Expected Dj= Rs. 5(1.15) = Rs. 5.75
Since, K_e = \(\frac{D_1}{p}\) + g
Therefore, K_e = \(\frac{5.75}{80}\) + 15% = 0.071875 + 0.15 = 0.221875 = 22.19%

(2) When anticipated growth rate changes to 16% and Cost of capital as calcu¬lated in (i) above ie. 22.19%, the indicative market price will be as follows.
P = \(\frac{D_1}{K_e-g}=\frac{5(1.16)}{0.2219-0.16}\) = Rs. 93.70 approx

Question 33.
Shares of Voyage Ltd. are being quoted at a price-earnings ratio of 8 times. The company retains 45% of its earnings which are ₹ 5 per share.
You are required to compute
1. The cost of equity to the company if the market expects a growth rate of 15% p.a. [May 2011] [3 Marks]
2. If the anticipated growth rate is 16% per annum, calculate the indicative market price with the same cost of capital. [3 Marks]
3. If the company’s cost of capital is 20% p.a. and the anticipated growth rate is 19% p.a., calculate the market price per share. [2 Marks]
Answer:
1. Cost of Capital
Retained earnings (45%) = ₹ 5 per share
Therefore, Dividend= (100 – 45)= (55%) = ₹ 6.11 per share
EPS (100%) = ₹ 11.11 per share
P/E Ratio = 8 times
Market price EPS × PE Ratio = ₹ 11.11 × 8 = ₹ 88.88
P₀ = \(\frac{D_1}{K_e-g}\)
Ke = \(\frac{R s .6 .11}{R s .88 .88}\) + 0.15 = 21.87%

2. Market Price if growth rate is 16%
P₀ = \(\frac{D_1}{K_e-g}=\frac{R s .6 .11}{(21.87 \%-16 \%)}\) = 104.08 per share

3. Market Price if growth rate is 19% and cost of capital is 20%
= \(\frac{R s .6 .11}{(20-1996)}\) = ₹ 611.00 per share

Question 34.
A company has a book value per share of ₹ 137.80. Its return on equity is 15% and follows a policy of retaining 60 per cent of its annual earnings. If the opportunity cost of capital is 18 per cent, what is the price of its share? [adopt the perpetual growth model to arrive at your solution). [Nov. 2011] [5 Marks]
Answer:
The Company’s earnings and dividend per share after a year are expected to be:
EPS = ₹ 137.80 × 0.15 = ₹ 20.67
Dividend = 0.40 × 20.67 = ₹ 8.27
The growth in dividend would be: e = 0.6 × 0.15 = 0.09

Perpetual growth model Formula : P₀ = \(\frac{\text { Dividend }}{K_e-g}\)
P₀ = \(\frac{8.27}{0.18-0.09}\)
P₀ = ₹ 91.89

Question 35.
In December, 2011 AB Co.’s share was sold for ₹ 146 per share. A long term earnings growth rate of 7.5% is anticipated. AB Co. is expected to pay dividend of 7 3.36 per share.
(i) What rate of return an investor can expect to earn assuming that dividends are expected to grow along with earnings at 7.5% per year in perpetuity?
(ii) It is expected that AB Co. will earn about 10% on book Equity and shall retain 60% of earnings. In this case, whether, there would be any change in grow th rate and cost of Equity? [May 2012] [6 Marks]
Answer:
(i) As per Dividend Discount Model approach the firm’s expected or required return on equity is computed as follows:
K_e = \(\frac{\text { Expected dividend at the end of year } 1\left(D_1\right)}{\text { Current Market Price }\left(P_0\right)}\) + Expected Growth Rate of Dividend
Therefore, K_e = \(\frac{3.36}{146}\) + 7.5%
= 0.230 + 0.075 = 0.098
K_e = 9.80%

(ii) When rate of return is 10% and retention ratio (b)is 60%, new growth rate will be as follows.
g = br
= 0.10 × 0.60 = 0.06
Thus dividend will also get changed and to calculate this, first we shall calculate previous retention ratio (b₁) and then EPS assuming that rate of return on equity (r) is same.
With previous Growth Rate of 7.5% and r= 10% the retention ratio comes out to be:
0.075 = b₁ × 0.10
b₁ = 0.75 and payout ratio = 0.25
With 0.25 payout ratio the EPS will be as follows:
\(\frac{3.36}{0.25}\) = 13.44
With new 0.40 (1 – 0.60) payout ratio the new dividend will be
D, = 13.44 × 0.40 = 5.376
Accordingly new K_e will be
K_e = \(\frac{5.376}{146}\) + 6.0%
K_e = 9.68%

Question 36.
Given the following information :

Current Dividend	₹ 5.00
Discount Rate	10%
Growth rate	2%

(i) Calculate the present value of the stock.
(ii) Is the stock over valued if the price is ₹ 40, ROE = 8% and EPS = ₹ 3.00
Show your calculations under the PE Multiple approach and Earnings Growth model. [Nov. 2012] [8 Marks]
Answer:
(i) Present Value of the Stock:
P₀ = \(\frac{5.00(1.02)}{0.10-0.02}\) = 63.75

(ii) Value of Stock under the PE Multiple Approach

Particulars	₹
Actual Stock Price	40.00
Return on equity	8%
EPS	3.00
PE Multiple (1/Return on Equity) =1/8%	12.50
Market Price per Share EPS × PE	37.50

Since, Actual Stock Price is higher, hence it is overvalued.

(iii) Value of the Stock under the Earnings Growth Model

Particulars	₹
Actual Stock Price	40.00
Return on equity	8%
EPS	3.00
Growth Rate	2%
Market Price per Share [EPS × (1+g)]/ (Ke -g) = ₹ 3.00 × 1.02/0.06	51.00

Since, Actual Stock Price is lower, hence it is undervalued.

Question 37.
X Limited, just declared a dividend of ? 14.00 per share. Mr. B is plan¬ning to purchase the share of X Limited, anticipating increase in growth rate from 8% to 9%, which will continue for three years. He also expects the market price of this share to be ? 360.00 after three years.
You are required to determine:
The maximum amount Mr. B should pay for shares, if he requires a rate of return of 13% per annum. [May 2013] [4 Marks]
(ii) The maximum price Mr. B will be willing to pay for share, if he is of the opinion that the 9% growth rate can be maintained indefinitely and require 13% rate of return per annum. [2 Marks]
(iii) The price of share at the end of three years, if 9% growth rate is achieved and assuming other conditions remaining same as in (ii) above.
Calculate rupee amount up to two decimal points.

	Year-1	Year-2	Year-3
FVIF @ 9%	1.090	1.188	1.295
FVIF @ 13%	1.130	1.277	1.443
PVlF @ 13%	0.885	0.783	0.693

Answer:
(i) Expected dividend for next 3 years.
Year 1 (D₁) ₹ 14.00 (1.09) = ₹ 15.26
Year 2 (D₂) ₹ 14.00 (1.09) = ₹ 16.63
Year 3 (D₃) ₹ 14.00 (1.09) = ₹ 18.13
Required rate of return = 13% (Ke)
Market price of share after 3 years = (P₃) = ₹ 360
The present value of share

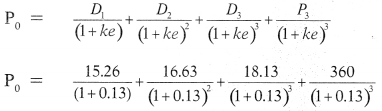
P₀ = 15.26 (0.885) + 16.63 (0.783) + 18.13 (0.693) + 360 (0.693)
P₀ = 13.50 + 13.02 + 12.56 + 249.48
P₀ = ₹ 288.56

(ii) When the growth rate 9% is achieved for indefinite period, then maximum price of share should Mr. A willing be to pay is
P₀ = \(\frac{D_1}{(k e-g)}=\frac{R s .15 .26}{0.13-0.09}=\frac{R s .15 .26}{0.04}\) = ₹ 381.50

(iii) Assuming that conditions mentioned above remain same, the price expected after 3 years will be:
P₃ = \(\frac{D_4}{k_e-g}=\frac{D_3(1.09)}{0.13-0.09}=\frac{18.13 \times 1.09}{0.04}=\frac{19.76}{0.04}\) = Rs. 494

Question 38.
The shares of G Ltd. are currently being traded at Rs. 46. The company published its result for the year ended 31st March, 2019 and declared a dividend of Rs.5. The company made a return of 15% on its capital and expects that to be the norm in which it operates. G Ltd. also expects the dividends to grow at 10% for the first three years and thereafter at 5%.
You are required to advise whether the share of the company is being traded at a premium or discount.
PVIF @ 15% for the next 3 year is 0.870, 0.756 and 0.658 respectively. [May 2019][8 Marks]
Answer:
Expected dividend for next 3 years.
Year 1 (D₁) =Rs. 5.00 (1.10) = Rs. 5.50
Year 2 (D₂) =Rs. 5.00 (1.10)² = Rs. 6.05
Year 3 (D₃) =Rs. 5.00 (1.10)³ = Rs, 6.655
After 3rd year, the dividends will grow at a normal rate of 5% till perpe-tuity.
Therefore, dividend in the year 4, (D₄) = (D₃)(1.05) = Rs. 6.655 (1.05) = Rs. 6.98775
Required rate of return = 15% (Ke)
= Rs. 69.8775
The present value of share

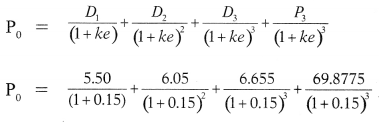
P₀ = 5.50 (0.870) + 6.05 (0.756) + 6.655 (0.658) + 69.8775 (0.658)
P₀ = 4.785 + 4.5738 + 4.3790 + 45.9794
P₀ = Rs. 59.7172
The share of the company is traded at discount. The intrinsic value of the share is Rs. 59.7172 (ex-dividend), whereas, the share is being traded at a price of Rs. 46 (assuming, cum-dividend). Therefore, the share is traded at a discount.

Question 39.
An investor is considering purchasing the equity shares of LX Ltd. whose current market price (CMP) is Rs. 150. The Company is proposing a dividend of Rs. 6 for the next year. LX is expected to grow @18 per cent per annum for the next four years. The growth will decline linearly to 14 per cent per annum after first four years. Thereafter, it will stabilize at 14 per cent per annum infinitely. The required rate of return is 18 per cent per annum.
You are required to determine:
(i) The intrinsic value of one share
(ii) Whether it is worth to purchase the share at this price.

Answer:
(i) Expected dividend for next 8 years.

After 9th year, the dividends will grow at a normal rate of 14% till perpetuity. Required rate of return = 18% (Ke)
Market price of share after 8 years = (P_s) = \(\frac{(\mathrm{D} 9)}{k e-g}=\frac{20}{0.18-0.14}\) = Rs. 500.00
The present value of share = Sum of dividends + Present value of price after 8 years.
P₀ = \(\frac{D_1}{(1+k e)}+\frac{D_2}{(1+k e)^2}+\frac{D_3}{(1+k e)^3}+\frac{D_4}{(1+k e)^4}+\frac{D_5}{(1+k e)^5}+\frac{D_0}{(1+k e)^6}+\frac{D_7}{(1+k e)^7}+\frac{D_8}{(1+k e)^8}+\frac{P_8}{(1+k e)^8}\)
P₀ = 39.83 + \(\frac{500}{(1+0.18)^8}\)
P₀ = 39.83 + 500 (0.266)
P₀ = 39.83 + 133 = Rs. 172.83
The intrinsic value of the share is = Rs. 172.83

(ii) The share of the company is traded at discount. The intrinsic value of the share is Rs. 172.83 whereas, the share is being traded at a price of Rs. 150. Therefore, the share is worth purchasing.
Note: There are two issues in this question:
(a) ‘The PVIF values for year 4 are given twice and are different, therefore, it y should be year 5 and not year 4 (it must be a misprint in the paper). The correction has been done.
(b) The growth rate is declining linearly from 18°o to 14%. But the question is silent as to the period over which the growth will decline, therefore, it is assumed that the 4°o decline is to occur gradually over a period of 4 years.

Question 40.
The current EPS of M/s VEE Ltd. is Rs. 4. The company has shown an extraordinary growth of 40% in its earnings in the last few years. This high growth rate is likely to continue for the next 5 years after which growth rate in earnings will decline from 40% to 10% during the next 5 years and remain stable at 10% thereafter. The decline in the growth rate during the five year transition period will be equal and linear. Currently, the company’s pay-out ratio is 10%. It is likely to remain the same for the next five years and from the beginning of the sixth year till the end of the 10,h year, the pay-out will linearly increase and stabilize at 50% at the end of the 10th year. The post tax cost of capital is 17% and the PV factors are given below :

You are required to calculate the intrinsic value of the company’s stock based on expected dividend. If the current market price of the stock is Rs. 125, suggest if it is advisable for the investor to invest in the company’s stock or not. [Nov. 2019 Old Syllabus] [8 Marks]
Answer:
Expected dividend for next 10 years.

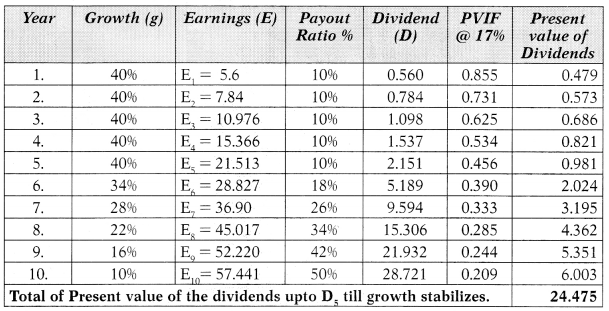
After 10th year, the dividends will grow at a normal rate of 10% till perpetuity.
Post tax cost of capital (Ke) = 17%
E₁₁ = E10 (1 + g) = 57.441 (1.10) = Rs. 63.186
D₁₁ = E₁₁ × Payout Ratio = 63.186 × 0.50
= Rs. 31.593
Market price of share after 10 years = (P₁₀) = \(\frac{\left(D_{11}\right)}{\mathrm{Ke}-\mathrm{g}}=\frac{31.593}{0.17-0.10}\) = Rs. 451.33
The present value of share (P₀) = Total PV of dividends + Present value of price after 10 years.
P₀ = 24.475 + 451.33 × (0.209)
P₀ = 24.475 + 94.33 = Rs. 118.80
The intrinsic value of the share is = Rs. 118.80
The intrinsic value of the share is Rs. 118.80 whereas, it is being traded at a price of Rs. 125.
The share of the company is traded at premium. Therefore, the investor is advised NOT to invest in this share.

Question 41.
A share of Tension – free Economy Ltd. is currently quoted at a price earnings ratio of 7.5 times. The retained earning being 37.5% is ₹ 3 per share.
Calculate:
(i) The company’s cost of equity, if investors’ expected rate of return is 12%.
(ii) Market price of share, if anticipated growth rate is 13% per annum with same cost of capital.
(iii) Market price per share, if the company’s cost of capital is 18% and anticipated growth rate is 15% per annum, assuming other conditions remaining the same. [Nov. 2013] [8 Marks]
Answer:
(i) Calculation of Cost of Capital: In the question investor’s expected rate of return can be assumed as rate of return on retained earnings and thus cost of equity shall be computed as follows:
g = b × r
g = 0.375 × 12% = 4.5%

Retained earnings	37.5%	₹ 3 per share
Dividend	62.5%	₹ 5 per share
EPS	100.0%	₹ 8 per share
P/E Ratio	7.5 times

Market price is ₹ 7.5 × 8 = ₹ 60 per share
Cost of equity capital = (Dividend/Price × 100) + growth %
= (5/60 × 100) + 4.59-6 = 12.8396
(\(\frac{R s .3}{37.5}\) + 62.5 = Rs. 5)
(ii) With the growth rate given (13%) the Market price of share shall become negative, which is not possible.
(iii) Market price = Dividend/(cost of equity capital % – growth rate %)
= 5/(18% – 15%)
= 5/3%
= ₹ 166.66 per share.

Question 42.
MNP Ltd. has declared and paid annual dividend of ? 4 per share. It is expected to grow @ 20% for the next two years and 10% thereafter.
The required rate of return of equity investors is 15%. Compute the current price at which equity shares should sell.
Note: Present Value Interest Factor (PVIF) @ 15%:
For year 1 = 0.8696;
For year 2 = 0.7561 [May 2014] [5 Marks]
Answer:
Dividend = ₹ 4 per share
growth rate = 20% for 2 years
10% thereafter
MV [Market Price] = \(\frac{D_1}{K_e-b r}\)

Years	Dividend
1	₹ 4 + 20% = 4.8
2	4.8 + 20% – 5.76
3	5.76 + 10% = 6.34

[P₂ = \(\frac{6.34}{15 \%-10 \%}=\frac{6.34}{5 \%}\)]
= ₹ 126.8 Price per share

PV of cash flows

Year	Cash Flow	Discounted Fac­tor	Discounted Cash Flow
1	4.8	0.8696	4.174
2	5.76	0.7561	4.355
2	126.8	0.7561	95.87
			104.402

Current price of the equity shares = ₹ 104.402 per share

Question 43.
XY Ltd., a Cement manufacturing Company has hired you as a financial consultant of the company. The Cement industry has been very stable for some time and the cement companies SK Ltd. & AS Ltd. are similar in size and have similar product market mix characteristic. Use comparable method to value the equity of XY Ltd. In performing analysis, use the following ratios:
(i) Market to book value
(ii) Market to replacement cost
(iii) Market to sales
(iv) Market to Net Income
The following data are available for your analysis:
(Amount in Rs.)

	SKLtd.	AS Ltd.	XY Ltd.
Market Value	450	400
Book Value	400	300	250
Replacement Cost	600	550	500
Sales	550	450	500
Net Income	18	16	14

[Nov. 2019 Old Syllabus] [5 Marks]
Answer:
Value of equity share of XY Ltd. using Comparable method and ratios.

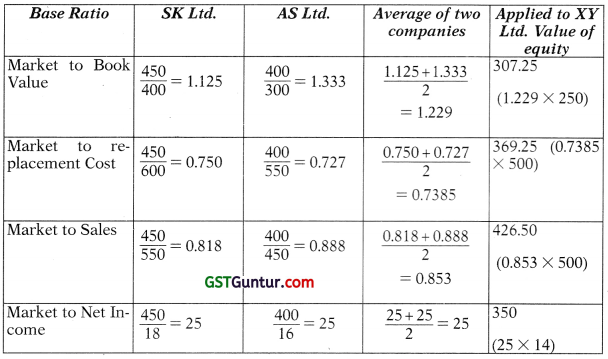
Value of XY Ltd. share = Simple Average of the Price Calculated based on 4 ratios.
= \(\frac{307.25+369.25+426.50+350}{4}\)
= \(\frac{1453}{4}\) = Rs. 363.25

Question 44.
You are interested in buying some equity stocks of RK Ltd. The company has 3 divisions operating in different industries. Division A captures 10% of its industries sales which is forecasted to be Rs. 50 crore for the industry. Divisions B and C captures 30% and 20% of their respective industry’s sales, which are expected to be Rs. 20 crore and Rs.8.5 crore respectively. Davison A traditionally had a 5% net income margin, w’hereas divisions B and C had 8% and lOWnet income margin respectively. RK Ltd. has 3,00,000 shares of equity stock outstanding, which sell at Rs. 250.
The company has not paid dividend since it started its business 10 years ago. However from the market sources you come to know that RK Ltd. will start paying dividend in 3 years time and the pay-out ratio is 30%. Expecting this dividend, you would like to hold the stock for 5 years. By analyzing the past financial statements, you have determined that RK Ltd.’s required rate of return is 18% and that P/E ratio of 10 for the next year and on ending P/E ratio of 20 at the end of the fifth year are appropriate.
Required:
(i) Would you purchase RK Ltd. equity at this time based on your one year forecast ?
(ii) If you expect earnings to grow @ 15% continuously, how much are you willing to pay for the stock of RK Ltd. ?
Ignore taxation.
PV factors are given below :

[Nov. 2019 Old Syllabus] [8 Marks]
Answer:
(i) Calculation showing whether the share of RK Ltd. he purchased or not:

Current P/E Ratio:
Total Earnings = 25 Lac + 48 Lac + 17 Lac = Rs. 90,00,000
No. of Shares = Rs. 3,00,000
Market Price of (MPS) Share = 250
EPS = \(\frac{90,00,000}{3,00,000}\) = Rs. 30
PE = \(\frac{\mathrm{MPS}}{\mathrm{EPS}}\) = \(\frac{250}{30}\) = 8.33

The P.E. Ratio is expected to be 10 for the next year. As the Company is not paying any dividend and there is an increase in P/E Ratio, the price after 1 year = 30 × 10 = 300.
Return = \(\frac{\mathrm{P}_1-\mathrm{P}_0}{\mathrm{P}_0}\) × 100 = \(\frac{300-250}{250}\) × 100
The return is more than required return of 18%. Therefore, RK Ltd.’s share should be purchased.

(ii) Calculation of Price If the earnings will grow @ 15% till perpetuity:

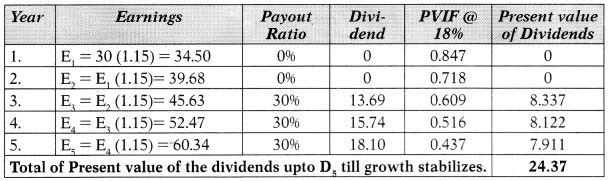
After 5th year, the dividends will grow at a normal rate of 15% till perpetuity.
Past tax cost of capitals = 18% (Ke)
D₆ = D₅ (1+ g) = 18.10 (1.15) = 20.815
Market price of share after 5 years = (P₅) = \(\frac{\left(D_6\right)}{\mathrm{Ke}-\mathrm{g}}=\frac{20.815}{0.18-0.15}\) = Rs. 694
Approx.
The present value of share = Sum of dividends + Present value of price after 5 years.
P₀ = 24.37 + \(\frac{694}{(1+0.18)^5}\)
P₀ = 24.37 + 694 (0.437)
P₀ = 24.37 + 303.28 = Rs. 327.65
The intrinsic value of the share is = Rs. 327.65 this is amount than can be paid for the stock of RK Ltd. It may be noted that fifth year price may also be taken on the bases of P/E ratio of 20 as given in the question.

Question 45.
You are requested to find out the approximate dividend payment ratio as to have the Share Price at ₹ 56 by using Walter Model, based on following information available for a Company.

	₹
Net Profit	50 lakhs
Outstanding 10% Preference Shares	80 lakhs
1 Number of Equity Shares	5 lakhs
Return on Investment	15%
Cost of Capital (after Tax) (k )	12%

Answer:
Calculation of Dividend Payout ratio

56 × 0.12 = D + 10.5 – 1.25 D
6.72 – 10.5 = -0.25 D
D = 15.12

Question 46.
The following information relates to Maya Ltd.:

Earnings of the company	₹ 10,00,000
Dividend payout ratio	60%
No. of shares outstanding	2,00,000
Rate of return on investment	15%
Equity capitalization rate	12%

(i) What would be the market value per share as per Walter’s model?
(ii) What is the optimum dividend payout ratio according to Walter’s model and the market value of company’s share at that payout ratio? [Nov. 2010] [8 Marks]
Answer:
(i) Computation of market-value per share as per Walter’s Model
P = \(\frac{D+\left(\frac{r}{k_e}\right)(E-D)}{k_e}\)
Market price per share
E = Earnings per share = ₹ 5
D = Dividend per share = ₹ 3
r = Return earned on investment = 15%
K_e = Cost of equity capital = 12%
∴ p = \(\frac{3+(5-3) \times \frac{0.15}{0.12}}{0.12}=\frac{3+2 \times \frac{15}{12}}{0.12}\) = Rs. 4.83

(ii) Optimum Dividend Pay out Ratio
As per Walter’s model, when the return on investment is more than the cost of equity capital the price per share increases as the dividend pay-out ratio decreases. Therefore, the optimum dividend pay-out ratio becomes zero. The market value of the company’s share will be :
= \(\frac{0+(5-0) \times \frac{.15}{.12}}{0.12}\) = ₹ 52.08

Question 47.
A company has an EPS of Rs. 2.5 for the last year and the DPS of Re.
1. The earnings is expected to grow at 2% a year in long run. Currently it is trading at 7 times its earnings. If the required rate of return is 14% compute
the following:
(i) An estimate of the P/E ratio using Gordon growth model.
(ii) The long-term growth rate implied by the current P/E ratio. [Nov. 2018] [8 Marks]
Answer:
Given:

Particulars
EPS0	2.5
DPS0	1
DPS1 = DPS0(l+g),	1(1.02) = 1.02
g	296
P.E Ratio	7%
Ke	14%

Price = \(\frac{D_1}{K_e-g}\)
(i) Estimate of P/E ratio using Gordon growth model

(ii) Long term growth rate implied by the current P.E ratio.

Question 48.
The following information is given for QB Ltd.

Earning per share	₹ 12
Dividend per share	₹ 3
Cost of capital	18%
Internal Rate of Return on investment	22%
Retention Ratio	40%

Calculate the market price per share using
(i) Gordon’s formula
(ii) Walters formula
Answer:
(i) Gordon’s Formula
P₀ = \(\frac{E(1-b)}{k-b r}\)
Where:
P₀ = Present value of Market price per share
E = Earnings per share
K = Cost of Capital
b = Retention Ratio (%)
r = rate of return
br = Growth Rate
P₀ = \(\frac{R s .12(1-0.40)}{0.18-(0.40 \times 0.22)}\)
= \(\frac{R s .7 .20}{0.18-0.088}=\frac{R s .7 .20}{0.092}\) = 78.26

(ii) Walter Formula
P₀ = \(\frac{D+\frac{r}{k}(E-D)}{k}\)
Where
P₀ = Market Price
D = Dividend per share
r = rate of return
k = Cost of Capital
E = Earnings per share
= \(\frac{R s .3+\frac{0.22}{0.18}(R s .12-R s .3)}{0.18}\)
= \(\frac{R s .3+R s .11}{0.18}\) = ₹ 77.77
Authprs Note : There is inconsistency in dividend paid and payout ratio

Question 49.
X Ltd. has an internal rate of return (5: 20%. It has declared dividend @ 18% on its equity shares, having face value of ₹ 10 each. The pay-out ratio is 36% and Price Earning Ratio is 7.25. Find the cost of equity according to Walter’s Model and hence determine the limiting value of its shares in case the pay-out ratio is varied as per the said model. [May 2012] [8 Marks]
Answer:
Rate of Return (r) = 0.20
Dividend (D) = 1.80
Earnings Per share (E) = \(\frac{1.80}{0.36}\) = 5
Price of share (P) = 5 × 7.25 = 36.25

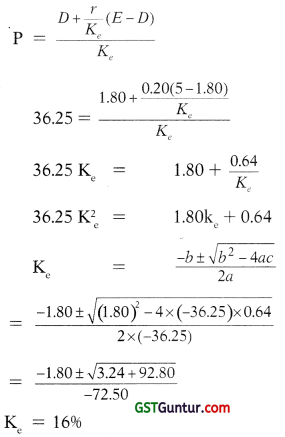
Since the firm is a growing firm, then 100% pay-out ratio will give limiting value of shares. At 100% payout, the price will be:
P = \(\frac{5.0+\frac{0.20(5-5)}{0.16}}{0.16}\)
= \(\frac{5.0}{0.16}\)
= ₹ 31.25
Thus limiting value is ₹ 1 1.25

Question 50.
X Ltd. earns ₹ 6 per share having a capitalization rate of 10 per cent and has a return on investment of 20% . According to Walter’s model, what
should be the price of the share at 25% dividend payout? [Nov. 2012] [5 Marks]
Answer:
As per Walter Model:
P₀ = \(\frac{D+\frac{r}{k_e}(E-D)}{k_e}\)
P₀ = Market value of the share
r = Return on retained earnings
Ke = Capitalization rate
E = Earnings per share
D = Dividend per share
Dividend per share = 25% of ₹ 6 = 1.5 ₹
Therefore, Price of the share

Question 51.
Goldilocks Ltd. was started a year back with equity capital of 40 lakhs.
The other details are as under:

Earnings of the company	4,00,000
Price Earnings ratio	12.5
Dividend paid	3,20,000
Number of Shares	40,000

Find the current market price of the share. Use Walter’s Model.
Find whether the company’s D/P ratio is optimal, use Walter’s formula. [Nov. 2014] [5 Marks]
Answer:
As per Walter’s Model:

As per Walter’s Model if ‘r’ is more than ‘k ’ optimal payout ratio for the firm is ‘NIL’. The company’s D/P ratio is not optimal.
So, if the payout ratio is zero, the market value of the company’s share will be:
= \(\frac{0+(10-0) \frac{0.10}{0.08}}{0.08}\) = ₹ 156.25

Question 52.
The following information is collected from the annual reports of J Ltd.:

Profit before tax	₹ 2.50 crores
Tax rate	40 per cent
Retention ratio	40 per cent
Number of outstanding shares	50,00,000
Equity capitalization rate	12 per cent
Rate of return on investment	15 per cent

What should be the market price per share according to Gordon’s model of dividend policy? [May 2015] [4 Marks]
Answer:
Profit after tax = ₹ 2.5 crore – 40%
= ₹ 1.5 crore
EPS per share = ₹ 1.5 crore/50,00,000 shares
= ₹ 3
As per Gordon’s formula P₀ = \(\frac{E(1-b)}{k-b r}\)
P₀ = Market price of the share
E = EPS
k = Cost of Capital
b = Retention ratio
r = return on equity
br = Growth rate
P₀ = \(\frac{R s .3(1-0.40)}{0.12-(0.4 \times 0.15)}\)
= \(\frac{1.8}{0.12-0.06}\)
= ₹ 30

Question 53.
M Ltd. belongs to a risk class for which the capitalization rate is 10%. It has 25,000 outstanding shares and the current market price is ₹ 100. IT expects a net profit of ₹ 2,50,000 for the year and the Board is considering dividend of ₹ 5 per share.
M Ltd. requires to raise ₹ 5,00,000 for an approved investment expenditure. Show, how does the MM approach affect the value of M Ltd., if dividends are paid or not paid. [May 2008] [8 Marks]
Answer:
A. When dividend is paid
(a) Price per share at the end of year 1
100= \(\frac{1}{1.10}\) (₹ 5 + P₁)
110 = ₹ 5 + P₁
P, = 105

(b) Amount required to be from issue of new shares
₹ 5,00,000 – (2,50,000 – 1,25,000)
₹ 5,00,000 – 1,25,000 = ₹ 3,75,000

(c) Number of additional shares to be issued
\(\frac{3,75,000}{105}\) = 3572 shares

(d) Value of M Ltd.
(Number of shares × Expected Price per share)
ie. (25,000 + 3,572) × ₹ 105 = ₹ 30,00,060

B. When dividend is not paid
(a) Price per share at the end of year 1
100 = \(\frac{P_1}{1.10}\)
P₁ = 110

(b) Amount required to be raised from issue of new shares
₹ 5,00,000 – 2,50,000 = 2,50,000

(c) Number of additional shares to be issued
\(\frac{2,50,000}{110}\) = 2273 shares (approx).

(d) Value of M Ltd.
(25,000 + 2,273) × ₹ 110
= ₹ 30,00,000

Conclusion:
Whether dividend is paid or not, the value of the firm remains the same

Question 54.
Buenos Aires Limited has 10 lakhs equity shares outstanding at the begin¬ning of the year 2013. The current market price is Rs. 150 and the directors have recommended a dividend of Rs. 9 per share. The rate of capitalization, appropriate to its risk class is 10%.
(i) Applying MM model calculate the fair price of the share when
(a) dividend is declared and
(b) dividend is not declared.
(ii) If the investment budget is Rs. 500 lakhs and anticipated profit is Rs. 200 lakhs, compute how many share are to be issued if
(a) dividend is declared and
(b) dividend is not declared. [Nov. 2014] [May 2018 Adapted][8 Marks]
Answer:
(i)

(ii) It is assumed that there is no retained fund. For the raising fund, equity shares to be issued at fair price as calculated above.

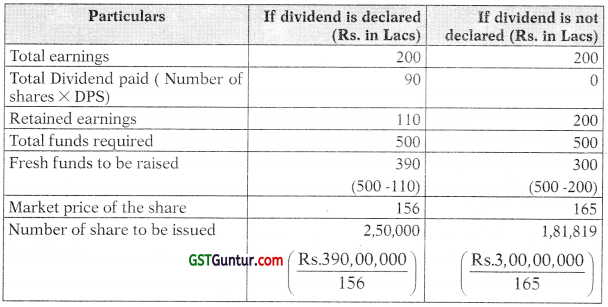
Question 55.
DEF Ltd. has been regularly paying a dividend of ₹ 19,20,000 per annum for several years and it is expected that same dividend would continue at this level in near future. There are 12,00,000 equity shares of ₹ 10 each and the share is traded at par.
The company has an opportunity to invest ₹ 8,00,000 in one year’s time as well as further ₹ 8,00,000 in two year’s time in a project as it is estimated that the project will generate cash inflow of ₹ 3,60,000 per annum in three year’s time which will continue forever. This investment is possible if dividend is reduced for next two years.
Whether the company should accept the project? Also analyze the effect on the market price of the share, if the company decides to accept the project. [May 2012] [8 Marks]
Answer:
Cost of Equity (K_e)

= – 6,89,655 – 5,94,530 + 1672,116.50
= Rs. 3,87,931.50

Conclusion:
As NPV of the project is positive, the value of the firm will increase by ₹ 3,87,931.50 and this value spread over the number of shares i.e. \(\frac{3,87,931.50}{12,00,000}\) = 0.323 the market price per share will increase by 32 paisa (appn.).

Question 56.
Wonderland Limited has excess cash of ₹ 20 lakhs, which it wants to invest in short term marketable securities. Expenses relating to investment will be ₹ 50,000.
The securities invested will have an annual yield of 9%.
The company seeks your advice
(i) as to the period of investment so as to earn a pre-tax income of 5%.
(ii) the minimum period for the company to break even its investment expenditure ignore time value of money. [Nov. 2014] [5 Marks]
Answer:
(i) Pre-tax income = ₹ 20 lakh × 5% = ₹ 1,00,000
T Expenses ₹ 50,000
₹ 1,50,000
Earnings in a year = ₹ 20,00,000 × 9% = ₹ 1,80,000
So Period of investment to earn ₹ 1,50,000
= 1,50,000 × \(\frac{12}{1,80,000}\) = 10 months

(ii) Break even income (B.E.I,) / Since expenses are ₹ 50,000, therefore B.E.I. = ₹ 50,000, It shall be earned in
= 50,000 × \(\frac{12}{1,80,000}\) = 3.33 months

Question 57.
X Ltd. is a Shoes manufacturing company. It is ail equity financed and has a paid-up Capital of ₹ 10,00,000 (₹ 10 per share)
X Ltd. has hired Swastika consultants to analyse the future earnings.
The report of Swastika consultants states as follows;
(i) The earnings and dividend will grow at 25% for the next two years.
(ii) Earnings are likely to grow at the rate of 10% from 3rd year and onwards.
(iii) Further, if there is reduction in earnings growth, dividend payout ratio will increase to 50%.
The other data related to the company are as follows:

You may assume that the tax rate is 30% (not expected to change in future) and post tax cost of capita! is 15%.
By using the Dividend Valuation Model, calculate
(i) Expected Market Price per share
(ii) P/E Ratio. [Nov. 2015] [6 Marks]
Answer:
(i) Dividend valuation Model:
P₀ = \(\frac{D_1}{K_e-g}\)
K_e = Cost of Capital
g = Growth rate
D₁ = Dividend at the end of year 1
On the basis of ike information given, the following projection can be made:

‘Payout Ratio changed to 50%.
After 2017, the perpetuity value assuming 10% constant growth is:
D₁ = ₹ 8.25 × 110% = ₹ 9.075
Therefore P₀ at the end of 2017
\(\frac{R s .9 .075}{0.15-0.10}\) × =Rs. 181.50
This must be discounted back to the present value, using the 3 year discount factor @ 15% which is 0.658.

(ii) P/E Ratio
P/E Ratio when P = 133.57 and E = 9.60
P/E Ratio = \(\frac{\text { Price }}{\text { Earning }}=\frac{133.57}{9.6}\) = 13.90

Question 58.
SAM Ltd. has just paid a dividend of ₹ 2 per share and it is expected to grow @ 6% p.a. After paying dividend, the Board declared to take up a project by retaining the next three annual dividends. It is expected that this project is of same risk as the existing projects. The results of this project will start coming from the 4th year onward from now. The dividends will then be ₹ 2.50 per share and will grow @ 7% p.a.
An investor has 1,000 shares in SAM Ltd. and wants a receipt of at least ₹ 2,000 p.a. from this investment.
Show that the market value of the share is affected by the decision of the Board. Also show as to how the investor can maintain his target receipt from the investment for first 3 years and improved income thereafter, given that the cost of capital of the firm is 8%. [May 2016] [8 Marks]
Answer:
Value of share at present = \(\frac{D_1}{K_e-g}\)
= \(\frac{2(1.06)}{0.08-0.06}\) = ₹ 106
However, if the Board implement its decision, no dividend would be payable for 3 years and the dividend for year 4 would be ₹ 2.50 and growing at 1% p.a. The price of the share, in this case, now would be:
P₀ = \(\frac{2.50}{0.08-0.07} \times \frac{1}{(1+0.08)^3}\) = ₹ 198.46
So, the price of the share is expected to increase from ₹ 106 to ₹ 198.45 after the announcement of the project. The investor can take up this situation as follows:

In order to maintain his receipt at ₹ 2,000 for first 3 year, he would sell
10 shares in first year @ ₹ 214.33 for ₹ 2,143.30
9 shares in second year @ ₹ 231.48 for ₹ 2,083.32
8 shares in third year @ ₹ 250 for ₹ 2,000.00
At the end of 3rd year, he would be having 973 shares valued @ ₹ 250 each i.e. ₹ 2,43,250. On these 973 shares, his dividend income for year 4 would be @ ₹ 2.50 i.e. ₹ 2,432.50. So, if the project is taken up by the company, the investor would be able to maintain his receipt of at least ₹ 2,000 for first three years and would be getting increased income thereafter.

Question 59.
XYZ Ltd. paid a dividend of ₹ 2 for the current year. The dividend is expected to grow at 40% for the next 5 years and at 15% per annum thereafter. The return on 182 days T-bills is 11% per annum and the market return is expected to be around 18% with a variance of 24%.
The co-variance of XYZ’s return with that of the market is 30%. You are required to calculate the required rate of return and intrinsic value of the stock. [May 2016] [8 Marks]
Answer:
Dividend = 2
Growth = 40% for 5 years
Growth = 15% after that
R_f = 11%
R_m = 18%
β = \(\frac{\text { Covariance of } X Y Z \text { with market }}{\text { Variance }}\) = 1.25
= \(\frac{30}{24}\) = 1.25
Required Rate of Return (As per CAPM) = R_t + β (R_m – R_f)
= 11 + 1.25 (18 – 11)
= 19.75%
Intrinsic value (The present value of future cash inflows)

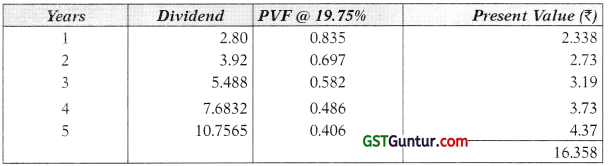
D₆ = D₅(1 + g)
= 10.7565(1.15)
= 12.37.
PV of Terminal Value = \(\frac{12.37}{0.1975-0.15} \times \frac{1}{(1.1975)^5}\) = 260.42 × 0.406 = 105.73
∴ Total Intrinsic Value = Rs. 16.358 + Rs. 105.73 = 122.088

Question 60.
Abinash is holding 5,000 shares of Future Group Limited. Presently the rate of dividend being paid by the company is ₹ 5 per share and the share is being sold at ₹ 50 per share in the market. However, several factors are likely to change during the course of the year as indicated below:

Risk free rate Market risk premium Expected growth rate Beta value
In view of the above factors whether Abinash should buy, hold or sell the shares? Narrate the reason for the decision to be taken. [May 2016] [8 Marks]
Answer:
Existing Rate of Return : (As per CAPM)
Return = R_f – β (R_m – R_f)
= 12.5 + 1.5 (6)
= 21.5%

Revised Rate of Return:
Return = R_f – β (R_m – R_f)
= 10+ 1.25 (4.8)
= 16%

Price of Share (Existing) :
P₀ = \(\frac{D_0(1+g)}{k_e-g}=\frac{5(1.05)}{0.215-0.05}=\frac{5.25}{0.165}\) = 31.82

Price of Share (Revised) :
P₀ = \(\frac{5(1.08)}{0.16-0.08}\) = 67.50

• Under Existing scenario, market price is ₹ 50 per share and equilibrium price is ₹ 31.82. So the shares need to be sold because they are over priced.
• Under Revised scenario, market price is ₹ 50, return is decreased but price is likely to increase, so, Mr. Abhilash should hold the shares.

Question 61.
Following Financial data are available for PQR Ltd. for the year 2008 :

	(₹ in lakh)
8% debentures	125
10% bonds(2007)	50
Equity shares (₹ 10 each)	100
Reserves and Surplus	300
Total Assets	600
Assets Turnovers ratio	1.1
Effective interest rate	8%
Effective tax rate	40%
Operating margin	10%
Dividend payout ratio	16.67%
Current market Price of Share	14
Required rate of return of investors	15%

You are required to :
(i) Draw income statement for the year
(ii) Calculate its sustainable growth rate
(iii) Calculate the fair price of the Company’s share using dividend discount model, and
(iv) What is your opinion on investment in the company’s share at current price? [Nov. 2009] [6 Marks]
Answer:
(i) Given :
Asset turnover ratio = 1.1
Total Assets = ₹ 600
Turnover (₹ 600 lakhs × 11) = ₹ 660 lakhs
Effective Interest rate = \(\frac{\text { Total Interest }}{\text { Total Liabilities }}=\frac{14}{175}\) × 100 = 8%
Liabilities = ₹ 125 lakhs + 50 lakhs = 175 lakhs
Interest = ₹ 175 lakhs × 0.08 = ₹ 14 lakhs
Operating Margin = 10%
Operating cost = (1 – 0.10) ₹ 660 lakhs = ₹ 594 lakh
Dividend Payout = 16.67%
Tax Rate = 40%
ROE = \(\frac{\text { PAT }}{\text { Net worth }(\mathrm{NW})}\) = ₹ 100 lakh + ₹ 300 lakh = 400 lakhs
ROE = \(\frac{R s .31 .2 \text { lakhs }}{R s .400 \text { lakhs }}\) × 100 = 7.8%
SGR = 0.078 (1 – 0.1667) = 6.5%

(iii) Calculation of fair price of share using dividend discount model

(iv) Since the current market price of share is ₹ 14 the share is overvalued. Hence the investor should not invest in the company.

Question 62.
Following Financial Data for Platinum Ltd. are available:

For the year 2011:	(₹ in lakhs)
Equity Shares (? 10 each)	100
8% Debentures	125
10% Bonds	50
Reserves and Surplus	200
Total Assets	500
Assets Turnover Ratio	1.1
Effective Tax Rate	30%
Operating Margin	10%
Required rate of return of investors	15%
Dividend payout ratio	20%
Current market price of shares	₹ 13

You are required to:
(i) Draw income statement for the year
(ii) Calculate the sustainable growth rate
(iii) Compute the fair price of the company’s share using dividend discount model, and
(iv) Draw your opinion on investment in the company’s share at current price. [Nov. 2012] [8 Marks]
Answer:
Working Notes:
Asset turnover ratio = 1.1
Total Assets = ₹ 500 lakhs
Turnover ₹ 500 lakhs × 1.1 = ₹ 550 lakhs
Effective interest = ₹ 125 lakhs × 0.08 + ₹ 50 lakhs × 0.10
= ₹ 15 lakh
Operating Margin = 10%
operating cost = (1 – 0.10) ₹ 550 lakhs = ₹ 495 lakh
Dividend Payout = 20%
Tax rate = 30%

(i) Income statement

	(₹ Lakhs)
Sale	550.00
Operating Exp.	495.00
EBIT	55.00
Interest (8% × 125 + 10% × 50)	15.00
EBT	40.00
Tax @ 30%	12.00
EAT	28.00
Dividend payout 20%	5.60
Retained Earnings	22.40

(ii) Computation of sustainable Growth Rate
SGR = G = ROE (1 – pay-out)
ROE = \(\frac{P A T}{\text { Net worth }}\), and NW = ₹ 100 lakhs + ₹ 200 lakhs = ₹ 300 lakhs
ROE = \(\frac{R s .28 \text { lakhs }}{R s .300 \text { lakhs }}\) × 100 = 9.33%
SGR = 0.0933 (1 – 0.20) = 7.47%

(iii) Computation of fair price of share using Dividend Discount Model

Conclusion:
Since the current market price of share is ₹ 13.00, the share is overvalued. Therefore the investor should not invest in the company.

Question 63.
Following Financial information are available for XP Ltd. for the year 2018:

For the year 2018:	(Rs. in lakhs)
Equity Share Capital (Rs. 10 each)	200
Reserves and Surplus	600
10% Debentures (Rs. 100 each)	350
Total Assets	1200
Assets Turnover Ratio	2 times
Tax Rate	30%
Operating Margin	10%
Dividend payout ratio	20%
Current market price of shares	Rs. 28
Required rate of return of investors	18%

You are required to :
(i) Prepare income statement for the year 2018.
(ii) Determine its sustainable growth rate.
(iii) Determine the fair price of the company’s share using dividend discount model.
(iv) Give your opinion on investment in the company’s share at current price. [May 2019] [8 Marks]
Answer:
Working Note:
Asset turnover ratio = 2 times
Total Assets = Rs. 1200 lakhs
Turnover Rs. 1200 lakhs × 2 = Rs. 2400 lakhs
Interest cost = Rs. 35 lakhs (350 lakhs × 0.10)
Operating Margin = 10%
Hence operating cost = (1-0.10) Rs. 2400 lakhs = Rs. 2160 lakhs
Dividend Payout = 20%
Tax rate = 30%

(i) Income statement

	(Rs. in Lakhs)
Sale	2400.00
Operating Exp.	2160.00
EBIT	240.00
Interest	35.00
EBT	205.00
Tax @ 30%	61.50
EAT	143.50
Dividend @ 20% of earnings	28.70
Retained Earnings	114.80

(ii) Determination of sustainable Growth Rate
SGR = G = ROE (1 – pay-out)
ROE = \(\frac{P A T}{N W}\) and NW = Rs. 200 lakhs + Rs. 600 lakhs = Rs. 800 lakhs
ROE = \(\frac{R s .143 .50}{R s .800 \text { lakhs }}\) × 100 = 17.9375%
SGR = 0.179375 (1 – 0.20) = 14.35%

(iii) Determination of fair price of share using Dividend Discount Model
P₀ = \(\frac{D_0(1+g)}{K_e-g}\)
Dividend per share = \(\frac{R s .28 .70 \text { lakhs }}{20 \text { lakhs }}\) = Rs. 1.435
Growth Rate = 14.35%
Hence P₀ = \(\frac{R s .1 .435(1+0.1435)}{0.18-01435}=\frac{R s .1 .6409}{0.0365}\)
= Rs. 44.956 = Rs. 45 approx.

(iv) Opinion:
Since the current market price of share is Rs. 28.00, the share is undervalued. Therefore the investor should invest in the company.

Question 64.
The risk free rate of return R_f is 9 per cent. The expected rate of return on the market portfolio R_m is 13 per cent. The expected rate of growth for the dividend of Platinum Ltd. is 7 per cent. The last dividend paid on the equity stock of firm A was ₹ 2.00. The beta of Platinum Ltd. equity stock is 1.2.
(i) What is the equilibrium price of the equity stock of Platinum Ltd.?
(ii) How would the equilibrium price change when

• The inflation premium increases by 2 per cent?
• The expected growth rate increases by 3 per cent?
• The beta of Platinum Ltd. equity rises to 1.3? [Nov. 2014] [8 Marks]

Answer:
(i) Equilibrium price of Equity using CAPM
= 9% + 1.2 (13% – 9%)
= 996 + 4.8% = 13.8%
P = \(\frac{D_1}{K_e-g}=\frac{2.00(1.07)}{0.138-0.07}=\frac{2.14}{0.068}\) = Rs. 31.47

(ii) New Equilibrium price of Equity using CAPM
= 9.1896 + 1.3 (1396 – 9.1896)
= 9.1896 + 4,966% = 14.14696
P = \(\frac{D_1}{K_e-g}=\frac{2.00(1.10)}{0.14146-0.10}=\frac{2.20}{0.04146}\) = ₹ 53.06

Question 65.
The risk free rate of return Rf is 5 per cent. The expected rate of return on the market portfolio R.n is 11 per cent. The expected rate of growth for the dividend of X Ltd. is 8 per cent. The last dividend paid on the equity stock of firm A was Rs. 2.00. The beta of X Ltd. equity stock is 1.5.
(i) What is the equilibrium price of the equity stock of X Ltd.?
(ii) How would the equilibrium price change when

• The inflation premium increases by 3 per cent?
• The expected growth rate increases by 3 per cent?
• The beta decreases to 1.3? [May 2018] [4 Marks]

Answer:
(i) Equilibrium price of Equity using CAPM
= 5% + 1.5(11% – 5%)
= 5% + 9% = 14%
P = \(\frac{D_1}{K_e-g}=\frac{2.00(1.08)}{0.14-0.08}\) = Rs. 36

(ii) New Equilibrium price of Equity using CAPM
= 5.15% + 1.3 (11% -5.15%)
= 5.15%+ 7.605%= 12.755%
P = \(\frac{D_1}{K_e-g}=\frac{2.00(1.11)}{0.12755-0.11}=\frac{2.22}{0.01755}\) = Rs. 126.50

Question 66.
Rahim Enterprises is a manufacturer and exporter of woolen garments to European countries. Their business is expanding day by day and in the previous financial year the company has registered a 25% growth in export business. The company is in the process of considering a new investment project. It is an ail equity financed company with 10,00,000 equity shares of face value of ₹ 50 per share. The current issue price of this share is ₹ 125 ex-dividend. Annual earnings are ₹ 25 per share and in the absence of new investments will remain constant in perpetuity. All earnings are distributed at present. A new investment is available which will cost ₹ 1,75,00,000 in one year’s time and will produce annual cash inflows thereafter of ₹ 50,00,000. Analyse the effect of the new project on dividend payments and the share price. [Nov. 2017] [8 Marks]
Answer:
Cost of Equity (KJ
D₁ = ₹ 25
P₀ = 125
K_e = \(\frac{D}{P}=\frac{R s .25}{125}\) = 20%
Therefore,
P/E = \(\frac{125}{25}\) = 5

NPV of the project :
NPV = \(\frac{-1,75,00,000}{(1+0.20)}+\frac{50,00,000}{0.20} \times \frac{1}{(1+0.20)}\)
= -1,45,83,333 + 2,08,33,333
= Rs. 62,50,000

Conclusion:
As NPV of the project is positive, the value of the firm will increase by ₹ 62,50,000 and ₹ 62,50,000 spread over the number of shares i.e., \(\frac{62,50,000}{10,00,000}\) the market price per share will increase by Rs. 6.25 per share.

Question 67.
Tiger Ltd. is presently working with an Earning Before Interest and Taxes (EBIT) of ₹ 90 lakhs. Its present borrowings are as follows:

	(₹ Lakhs)
12% term loan	300
Working capital borrowings:
From Bank at 15%	200
I Public Deposit at 11%	100

The sales of the company are growing and to support this, the company proposes to obtain additional borrowing of ₹ 100 lakhs expected to cost 16%.
The increase in EBIT is expected to be 15%.
Calculate the change in interest converge ratio after the additional borrowing is effected and comment on the arrangement made. [Nov. 2012] [8 Marks] [June 2009] [6 Marks]
Answer:
Computation of Present Interest Coverage Ratio
Present EBIT = ₹ 90 lakhs

Interest Charges (Present)	(₹ Lakhs)
Term loan @ 12%	36.00
Bank Borrowings @ 15%	30.00
Public Deposit @ 11%	11.00
	77.00

Present Interest Coverage Ratio = \(\frac{E B I T}{\text { Interest Charges }}\)
\(\frac{R s .90 \text { lakhs }}{R s .77 \text { lakhs }}\) = 1.169

Calculation of Revised Interest Coverage Ratio
Revised EBIT (115% of × 90 lakhs) = ₹ 103.50 lakhs
Proposed interest charges
Existing charges = ₹ 77.00 lakhs
ThW: Additional charges (16% of additional = ₹ 16.00 lakhs
Borrowings i.e. = ₹ 100 lakhs)
Total = ₹ 93.00 lakhs

Revised Interest Coverage Ratio = \(\frac{R s .103 .50 \text { lakhs }}{R s .93 .00 \text { lakhs }}\) = 1.113
Thus, with the proposed increase in the sales the burden of interest on additional borrowings of ₹ 100 lakhs will adversely affect the interest coverage ratio which has been reduced, (i.e. from 1.169 to 1.113). Therefore, the proposal is not worth implementing.

Question 68.
AMKO limited has issued 75,000 equity shares of ₹ 10 each. The current market price per share is ₹ 36. The company has a plan to make a right issue of one new equity share at a price of ₹ 24 for every four shares held.
You are required to:
(i) Calculate the theoretical post-rights price per share.
(ii) Calculate the theoretical value of the right alone. [Nov. 2018 Old Syliabus][4 Marks]
Answer:
Ex-Right Price = \(\frac{(\text { No. of Existing Shares } \times \text { Existing Price })+(\text { Right Shares } \times \text { Right Price })}{\text { No. of existing Shares }+ \text { Right Shares }}\)
= \(\frac{(4 \times 36)+(1 \times 24)}{4+1}=\frac{168}{5}\) = ₹ 33.60
Value of Right = Existing Price – Ex-Right Price = ₹ 36 – 33.60 = ₹ 2.40

Question 69.
ABC Limited’s shares are currently selling at ₹ 13 per share. There are 10,0, 000 shares outstanding. The firm is planning to raise ₹ 20 lakhs to finance a new project.
Required:
What are the ex-right price of shares and the value of a right, if
(i) The firm offers one right share for every two shares held.
(ii) The firm offers one right share for every four shares held.
(iii) How does the shareholders’ wealth change from (i) to (ii)? How does right issue increases shareholders’ wealth? [Nov. 2004] [6 Marks]
Answer:
(i) When the firm offers one Right Share for every two shares held:
Number of shares to be issued = 10,00,000 × \(\frac{1}{2}\) = 5,00,000 Shares
Amount to be raised = ₹ 20,00,000
Therefore, Right Price = ₹ 20,00,000 ÷ 5,00,000 = ₹ 4 per share

Ex-Right Price = \(\frac{(\text { No. of Existing Shares } \times \text { Existing Price })+(\text { Right Shares } \times \text { Right Price })}{\text { No. of existing Shares }+ \text { Right Shares }}\)
= \(\frac{(10,00,000 \times R s .13)+(5,00,000 \times R s .4)}{10,00,000+5,00,000}\) = ₹ 10
Value of Right = Existing Price – Ex-Right Price = ₹ 13 – ₹ 10 = ₹ 3

(ii) When the firm offers one right share for every four shares held:
Number of shares to be issued = 10,00,000 × \(\frac{1}{4}\) = 2,50,000 Shares
Amount to be raised = ₹ 20,00,000
Therefore, Right Price = ₹ 20,00,000 + 2,50,000 = ₹ 8 per share

Ex-Right Price = \(\frac{(\text { No. of Existing Shares } \times \text { Existing Price })+(\text { Right Shares } \times \text { Right Price })}{\text { No. of existing Shares }+ \text { Right Shares }}\)
= \(\frac{(10,00,000 \times R s .13)+(2,50,000 \times R s .8)}{10,00,000+2,50,000}\) = ₹ 12
Value of Right = Existing Price – Ex-Right Price = ₹ 13 – ₹ 12 = Re. 1

(iii) Calculation of effect of right issue on Shareholder’s wealth:
Let us consider the case of a shareholder who is holding 100 shares.
(a) When firm offers one share for two shares held.

Value of Shares after right issue (150 × ₹ 10) (Total No. of Shares × Ex-Right Price)	₹ 1,500
Less: Amount paid to acquire right shares (50 × ₹ 4)	₹ 200
Value of Shares AFTER Right Issue	₹ 1,300
Value of Shares before Right Issue (100 × ₹ 13)	₹ 1,300
Effect of right issue on Shareholder’s wealth	No Effect

(b) When firm offers one share for every four shares held.

Value of Shares after right issue (125 × ₹ 12) (Total No. of Shares X Ex-Right Price)	₹ 1,500
Less: Amount paid to acquire right shares (25 × ₹ 8)	₹ 200
Value of Shares AFTER Right Issue	₹ 1,300
Value of Shares before Right Issue (100 × ₹ 13)	₹ 1,300
Effect of right issue on Shareholder’s wealth	No Effect

Question 70.
Eager Ltd. has a market capitalization of ₹ 1,500 crores and the current market price of its share is ₹ 1500. It made a PAT of 200 crores and the Board is considering a proposal to buy back 20% of the shares at a premium of 10% to the current market price. It plans to fund this through a 16% bank loan. You are required to calculate the post buy back earning per share (EPS). The company’s corporate tax rate is 30%. [Nov. 2018 old syllabus] [5 Marks]
Answer:
Number of Shares = \(\frac{1500}{1500}\) = 1 Crores
PAT = 200 Crores
Number of Shares Bought Back = 20 lakhs (20% of 1 crore)
Number of shares after buy-back = 80 lakhs
Price of buy-back = 1500 +10% = ₹ 1650
Amount of Loan @16% = 20 lakhs × 1,650
= ₹ 33000 lakhs
Interest on loan = ₹ 5,280 lakhs
Interest cost after tax @30% = ₹ 3,696 lakhs
New EPS = \(\frac{200-36.96}{0.8}=\frac{163.04}{0.8}\)
= ₹ 203.80 per share

Question 71.
ABB Ltd. has a surplus cash balance of ₹ 180 lakhs and wants to distribute 50% of it to the equity shareholders. The company decides to buy-back equity shares. The company estimates that its equity share price after re-purchase is likely to be 15% above the buy-back price, if the buy-back route is taken.
Other information is as under:
(si) Number of equity shares outstanding at present (Face Value × 10 each) is 20 lakhs.
(2) The current EPS is ₹ 5.
You are required to calculate the following:
(i) The price at which the equity shares can be re-purchased, if market capitalization of the company should be ₹ 400 lakhs after buy-back.
(ii) Number of equity shares that can be re-purchased.
(iii) The impact of equity shares re-purchase on the EPS, assuming that the net income remains unchanged. [May 2019 New Syllabus] [8 Marks]
Answer:
(i) Determination of Buy-Back Price, if market capitalization of the company should be ₹ 400 lakhs after buy-back.
Let the buy-back price be ₹ x
Surplus Cash = ₹ 180 Lakhs
Amount utilised for Buy-Back (₹ 180 Lakhs X 50%) = ₹ 90 Lakhs
Therefore, number of shares bought back = \(\frac{\text { Rs. } 90 \text { Lakhs }}{\text { Rs. X }}\)
Number of shares left after buy-back = 20,00,000 – \(\frac{\text { Rs. } 90 \text { Lakhs }}{\text { Rs. X }}\)
Market price after buy-back = 115% of ₹ X = 1.15X

Market capitalisation after buy-back
= No. of shares after buy-back X Market price after buy-back
= [20,00,000 – \(\frac{\text { Rs. } 90 \text { Lakhs }}{\text { Rs. X }}\)] × 1.15 X {It should be equal to ₹ 400 Lakhs}
400 Lakhs = [20,00,000 – \(\frac{\text { Rs. } 90 \text { Lakhs }}{\text { Rs. X }}\)] × 1.15X

By solving for X
X = ₹ 21.89
Hence, the share should be re-purchased @ ₹ 21.89.

(ii) Calculation of number of equity shares that can be re-purchased.
Number of Shares brought back = \(\frac{\text { Rs. } 90 \text { Lakhs }}{\text { Rs. X }}=\frac{\text { Rs.90 Lakhs }}{\text { Rs. } 21.89}\)
= 4,11,147 Shares

(iii) Determination of impact of buy-back on the EPS:
Number of shares after buy-back = 20,00,000 – 4,11,147 Shares = 15,88,853
Total Earnings = No. of shares before Buy-Back × Current EPS = 20,00,000 × ₹ 5 = ₹ 100 Lakhs
EPS = \(\frac{\text { Earnings }}{\text { No. of shares }}=\frac{\text { Rs.100 Lakhs }}{15,88,853}\) = ₹ 6.29
So EPS increases by 1.29.

Question 72.
Rahul Ltd. has a surplus cash balance of ? 100 lakhs and wants to distribute 27% of it to the equity shareholders. The company decides to buyback equity shares. The company estimates that its equity share price after re-purchase is likely to be 10% above the buyback price, if the buyback route is taken. The number of equity shares outstanding at present (Face Value ₹ 10 each) is 10 lakhs and the current EPS is ₹ 3.
You are required to determine:
(i) The price at which the equity shares can be re-purchased, if market capitalization of the company should be ₹ 210 lakhs after buy-back.
(ii) Number of equity shares that can be re-purchased.
(in) The impact of equity shares re-purchase on the EPS, assuming that the net income remains unchanged. [Nov. 2010] [8 Marks]
Answer:
(1) Determination of Buy-Back Price, if market capitalization of the company should be 1210 lakhs after buy-back.
Let the buy-back price be ₹ x
Surplus Cash = ₹ 100 Lakhs
Amount utilised for Buy-Back (₹ 100 Lakhs × 27%) = ₹ 27 Lakhs
Therefore, number of shares bought back = \(\frac{\text { Rs.27 Lakhs }}{\text { Rs. X }}\)
Number of shares left after buy-back = 10,00,000 – \(\frac{\text { Rs.27 Lakhs }}{\text { Rs. X }}\)
Market price after buy-back = 110% of ₹ X = 1.10X

Market capitalisation after buy-back
= No. of shares after buy-back × Market price after buy-back
= [10,00,000 – \(\frac{\text { Rs. } 27 \text { Lakhs }}{\text { Rs. X }}\)] × 1.10X {It should be equal to ₹ 210 Lakhs}
210 Lakhs = [10,00,000 – \(\frac{\text { Rs. } 27 \text { Lakhs }}{\text { Rs. X }}\)] × 1.10 X

By solving for X
X = ₹ 21.79
Hence, the share should be re-purchased @ ₹ 21.79.

(ii) Calculation of number of equity shares that can be re-purchased.
Number or shares bought back = \(\frac{\text { Rs.27 Lakhs }}{\text { Rs. X }}=\frac{\text { Rs.27 Lakhs }}{\text { Rs.21.79 }}\)
= 1,23,910 Shares

(iii) Determination of impact of buy-back on the EPS:
Number of shares after buy-back = 10,00,000 – 1,23,910 Shares
= 8,76,090 Shares
Total Earnings = No. of shares before Buy-Back × Current EPS
= 10,00,000 × ₹ 3 = ₹ 30 Lakhs
EPS = \(\frac{\text { Earnings }}{\text { No. of shares }}=\frac{\text { Rs.30 Lakhs }}{8,76,090 \text { im }}\) = ₹ 3.424

Question 73.
Mr. A is thinking of buying shares at ₹ 500 each having face value of ₹ 100. He is expecting a bonus at the ratio of 1:5 during the fourth year. Annual expected dividend is 20% and the same rate is expected to be maintained on the expanded capital base. He intends to sell the shares at the end of seventh year at an expected price of ₹ 900 each. Incidental expenses for purchase and sale of shares are estimated to be 5% of the market price. He expects a minimum return of 12% per annum. Should Mr. A buy the share? If so, what maximum price should he pay for each share? Assume no tax on dividend income and capital gain. [May 2010] [4 Marks]
Answer:
P.V. of dividend stream and sales proceeds

Year	Dividend/Sale	PVF (12%)	PV(₹)
1	₹ 20	0.893	17.86
2	₹ 20	0.797	15.94
3	₹ 20	0.712	14.24
4	₹ 24	0.636	15.26
5	₹ 24	0.567	13.61
6	₹ 24	0.507	12.17
7	₹ 24	0.452	10.85
7	₹ 1,026 (₹ 900 × 1.2 × 0.95)	0.452	463.75
	LESS: Cost of share (₹ 500 × 1.05)		₹ 563.68 ₹ 525.00
	Net gain		₹ 38.68

Since Mr. A is gaining ₹ 38.68 per share, he should buy the share.
Maximum price: Mr. A should be ready to pay is ₹ 563.68 which will include incidental expenses. So the maximum price should be ₹ 563.68 × (100/105), which comes at ₹ 536.84