Mutual Funds – CA Final SFM Study Material

Mutual Funds – CA Final SFM Study Material is designed strictly as per the latest syllabus and exam pattern.

Mutual Funds – CA Final SFM Study Material

Part – I (Theory)

Question 1.
Discuss briefly the advantages of investing through Mutual Funds. [May 2003, 2007, 2009] [4 Marks]
Answer:
The following are the benefits of investing through mutual fund schemes:
1. Professional Management: The funds are managed by highly skilled and professionally experienced managers with a backup of a research team.

2. Diversification : A small investor cannot hold diversified investment portfolio wdth low level of investible funds. But, he may take advantage of a well-diversified portfolio of securities with the help of mutual fund. It reduces the risk also.

3. Convenient Administration :Now-a-days most of the mutual funds offer services in a demat form which saves the time and also avoids delay in execution of transaction. So, there are no administrative risks of share transfer, etc.

4. High Returns : If we compare mutual fund with other avenues of the investment, then the investor always get higher return in mutual fund.

5. Liquidity : The investment in any mutual fund can be liquidated at any time. In case of open ended funds, the liquidity is provided by direct sales/ repurchase to the mutual fund. On the other hand, the stock exchange, at which the mutual fund is listed, provides liquidity in case of close ended funds.

6. Low Cost of Management: The mutual fund is not allowed to incur the cost beyond prescribed limit of 2.5%. Any cost in excess of this maximum limit is borne by the AMC.

7. Safety : The mutual funds are required to be registered with SEBI and are subject to strict mutual fund regulations. It provides protection to investor.

8. Transparency : The investor gets updated information about the funds. Many mutual funds disclose their portfolio on quarterly or monthly basis to their investors. Even, in case of open ended funds, the NAV is calculated on a daily basis and now published through AMFI in the newspapers.

9. Low transaction cost : The mutual funds uses pooled money from a number of investors due to which, they have advantage of economies of scale. That is why; it is beneficial for the investor as compared to direct investment in capital market which involves higher charges.

10. Flexibility : The investors can easily transfer their holdings from one scheme to another scheme within the same mutual fund. The wide range of schemes launched by different mutual funds provides flexibility to the investor to plan his portfolio.

Question 2.
What are the drawbacks of investments in Mutual Funds? [Nov. 2008] [4 Marks]
Answer:
The following are the disadvantages associated with mutual fund schemes:
1. Difficulty in selection : A common investor faces difficulty in selection of mutual fund out of large number of various schemes of mutual funds. The past performance may not prove to be reliable criterion in all situations.

2. Cost Factor: The entry load (payable at the time of investment) and exit load (payable at the time of leaving) reduce the return of investor. Moreover, the fee paid to Asset Management Company is not related with performance.

3. Different Objectives : The individual objectives of the investor may be different from the objectives of mutual fund. The skilled or professional investors or high net worth individuals may achieve their objectives through direct investment mode.

4. No Guarantee of Return : There is no guarantee of return in case of mutual fund as it depends upon performance of fund only. If it under performs, there are chances of depreciation in value of investment even with depletion of principal amount.

5. Unethical Practices /The investment in mutual funds is subject to risk from unethical practices like selling of holding to sister concern for substantive notional gains so that higher NAY may be disclosed.

Question 3.
Distinguish between Open-ended and close ended schemes. [Nov. 2010, May 2015] [4 Marks]
Answer:
The Mutual funds may be classified as open ended and close ended, on functional basis.
1. Open ended funds : These are the schemes floated by the mutual fund, where the investor can make entry and may exit at any time. The redemption period is indefinite and the capital of the fund is unlimited. These schemes are available for subscription and repurchase on a continuous basis. These funds are most liquid.

2. Closed ended Funds : Under these schemes, the investor can enter into the scheme during Initial Public Offering or from the stock market after the units have been listed. The life of these schemes is limited as after the specified period, the corpus of the closed ended schemes is liquidated. If the investor wants to exit in between, he can do so by selling units in the secondary market, or during repurchase period at his option.

Basis	Open ended fund	Close ended fund
Size of the fund	Unlimited and Flexible	Limited and Fixed
Redemption period	At the option of Investor	Stipulated Maturity Period
Intra-day Trading	Not possible	Possible but expensive
Exit Route	Through fund itself	Through stock exchange, Where listed
Selling Rate	At NAV plus load, if any	Significant Premium/Discount to NAV.

Question 4.
What is Exchange Traded Funds? What are its key features and benefits? [May 2010, Nov. 2013, Nov. 2016] [4 Marks]
Answer:
The exchange traded funds were introduced in US in 1993 and came to India around 2002. ETF is a hybrid product that combines the features of an index mutual fund and stock. It is a portfolio or basket of securities that replicates the composition of indices like Nifty, Sensex etc. It is not a stock or security by itself, but is traded as stock. ETF are listed on the stock exchange and their prices are linked to the underlying index.
The ETF can be bought or sold anytime during the market hours at prices that are expected to be closer to the NAV at the end of the day. The NAV of an ETF is the value of the underlying component of the benchmark index held by the ETF plus all accrued dividends less accrued management expenses.
The following are the benefits of ETF:
(a) Convenient to Trade : The ETF can be purchased/sold on the stock ex-change at any time when the market is open.
(b) Diversification / These funds offer diversification and also the flexibility at the same time.
(c) Short Selling/ One can short sell an ETF, which is not possible with index funds.
(d) Role of Fund Manager: The performance of ETF does not depend on the ability of fund manager.
(e) Convenient to Trade / When the trading starts in market, the investor can easily buy or sell ETF like equity shares at prices which are deemed real time.

Question 5.
Write short note on Money Market Mutual Fund. [Nov. 2011, 2015] [4 Marks]
Answer:
They are majorly debt-oriented schemes, where the main objective is to preserve the capital, easy liquidity and moderate income. The investments are made in short-term instruments which have high safety like, T-Bills, Govern-ment securities, certificate of deposit etc. These are suitable for institutional investors and individuals who have short term surplus funds. As they are for short period, they have lesser risk and are not affected by interest rate fluctuations.

The following are the salient features:

• Money market is that part of financial market which is for short term money.
• These schemes are safe and highly liquid instruments.
• These schemes generally provide high returns and highest safety to the ordinary investors.
• The short term/emergency requirements of various funds are met by such mutual funds.

Question 6.
What are the signals that indicate that it is the time for an investor to exit a mutual fund schemes? [Nov. 2014] [4 Marks]
Answer:
The following are the signals/indicators that investors use as exit criteria from the mutual fund scheme:
1. Under performance of mutual fund : The under performance criterion has two parameters:
(a) FROM INDEX : When the mutual fund consistently under performs its peer group, then it would be better to get out of the scheme. The amount may be invested in the winning schemes of peer group.
(b) FROM PEER GROUP : When the mutual fund consistently under per-forms the broad based index, then it is the high time for the investor to get out of the scheme.

2. Change in objectives : The mutual funds have various schemes with varying objectives. The investor chooses a particular scheme that suits his purpose. As regards indicators to exit, there are two aspects:
(a) OF MUTUAL FUND : Every investor works with his own risk prefer-ences and selects that scheme of the mutual fund which suits his goals. It may be regular income or growth fund. When the mutual fund changes its objective (Like from income to growth fund), then the investor may exit that mutual fund scheme.
(b) OF INVESTOR : When the investor changes his objective of investing in a mutual fund which is no longer beneficial to him, then it is also one of the indicators to exit a scheme.

3. Change in Fund Management /When there is change in the fund manager who handles the scheme and the image or reputation of new entrant is not known, then the investor may exit the mutual fund scheme.

Question 7.
Distinguish between Off-Shore Funds and Asset Management Mutual Funds. [Nov. 2017] [4 Marks]
Answer:
The following are the differences:

Basis	Off-shore Funds	Mutual Funds
Raising of Money	Internationally and investing money domestically (in India).	Domestically as well as investing money domestically (in India).
Number of Investors	Very few.	Very large.
Per Capita investment	It is very high as investors are High Net worth Individuals (HNI).	It is very low as it is meant for retail/ small investors.
Basis of Management	Investment Agreement is basis of management of the fund.	Offer Document is the basis of management of the fund.

Question 8.
Explain the different methods for evaluating the performance of a mutual fund. [Nov. 2019 Old Syllabus] [4 Marks]
Answer:
Methods for evaluating the performance of a mutual fund.
1. Sharpe Ratio
The excess return earned over the risk free return on portfolio to the portfolio’s total risk measured by the standard deviation. This formula uses the volatility of portfolio return. The Sharpe ratio is often used to rank the risk-adjusted performance of various portfolios over the same time. The higher a Sharpe ratio, the better a portfolio’s returns have been relative to the amount of investment risk the investor has taken.
S = \(\frac{\text { Return of portfolio }- \text { Retrun of risk free investment }}{\text { Standard Deviation of Portfolio }}\)

2. Treynor Ratio
This ratio is similar to the Sharpe Ratio except it uses Beta of portfolio instead of standard deviation. Treynor ratio evaluates the performance of a portfolio based on the systematic risk of a fund. Treynor ratio is based on the premise that unsystematic or specific risk can be diversified and hence, only incorporates the systematic risk (beta) to gauge the portfolio’s performance.
T = \(\frac{\text { Return of portfolio }- \text { Retrun of risk free investment }}{\text { Beta of Portfolio }}\)

3. Jensen’s Alpha
The comparison of actual return of the fund with the benchmark portfolio of the same risk. Normally, for the comparison of portfolios of mutual
funds this ratio is applied and compared with market return. It shows the comparative risk and reward from the said portfolio. Alpha is the excess of actual return compared with expected return.

Part – 2 (Numerical Problems: Topic Wise In Chronological Order)

Question 1.
Cinderella Mutual Fund has the following assets in Scheme Rudolf at the close of business on 31st March, 2014.

Company	No. of Shares	Market Price Per Share (Rs.)
Nairobi Ltd.	25,000	20
Dakar Ltd.	35,000	300
Senegal Ltd.	29,000	380
Cairo Ltd.	40,000	500

The total number of units of Scheme ‘Rudolf’ is 10 lacs. The Scheme Rudolf has accrued expenses of Rs. 2,50,000 and other liabilities of Rs. 2,00,000. Calculate the NAV per unit of the Scheme Rudolf. [Nov. 2014] [4 Marks]
Answer:
Calculation of Closing Net Assets

	Rs. in crores
Market Value of Portfolio[Working Note-1]	82.954
(+) Closing cash in hand	2.760
(+) Dividend Accrued	1.950
Total Closing Assets	87.664
(-) Payable on shares	(13.54)
(-) Expenditure incurred  .	(1.76)
Closing Net Assets	72.364

NAV per unit = \(\frac{\text { Closing Net Assets }}{\text { Number of Units }}=\frac{\text { Rs. } 4,15,70,000}{10,00,000}\) = Rs. 41.57 per unit

Working Note-1 Computation of Market Value of Investments

Company	No. of Shares	Market Price per share	Total Market Value
Nairobi Ltd.	25,000	20	5,00,000
Dakar Ltd.	35,000	300	1,05,00,000
Senegal Ltd.	29,000	380	1,10,20,000
Cairo Ltd.	40,000	500	2,00,00,000
			4,20,20,000

Question 2.
Calculate the NAV of a regular income scheme on per unit basis of Red Bull mutual fund from the following information:

Particulars	Rs. in crores
Listed shares at cost (ex-dividend)	30
Cash in hand	0.75
Bonds & Debentures at cost (ex-interest)	2.30
Of these, bonds not listed & not quoted	1.0
Other fixed interest securities at cost	2.50
Dividend accrued	0.8
Amount payable on shares	8.32
Expenditure accrued	1.00
Value of listed bonds & debentures at NAV date	10

Additional Information:
(1) Number of units ( Rs. 10 face value) = 30 lakhs
(2) Current realizable value of fixed income securities of face value of Rs. 100 is 106.50.
(3) The listed shares were purchased when index was the Present index is 7100 and 9000.
(4) Unlisted bonds and debentures are at cost. Other fixed interest securities are also at cost. [May 2016] [6 Marks]
Answer:
Calculation of Closing Net Assets

	Rs. in crores
Market Value of Portfolio [Working Note-1] (+) Closing cash in hand (+) Dividend Accrued	51.53 0.75 0.80
Total Closing Assets (-) Payable on shares (-) Expenditure incurred	53.08 (8.32) (1.00)
Closing Net Assets	43.76

NAV per unit = \(\frac{\text { Closing Net Assets }}{\text { Number of Units }}=\frac{\text { Rs. } 43.76 \text { crores }}{30 \text { Lakh Units }}\)
= \(\frac{\text { Rs. } 4376 \text { Lakhs }}{\text { 30 Lakh Units }}\) = Rs. 145.87 per unit

Working Note-1 Calculation of Market Value of Portfolio

Particulars	Workings	Rs. in crores
Listed Shares	(30 × 9000)/7100	38.03
Unlisted Bonds (Unquoted)	(at cost)	1.00
Listed Bonds & Debentures	(value is given)	10.00
Other Fixed Interest Securities	Tutorial Note	2.50
		51.53

Tutorial Note:
The current realizable value of fixed income securities has no relevance in the given problem as it is to be valued at cost, as per the instruction given in the question. Had this instruction not been given, then the value would have been calculated as follows:
Value = \(\frac{2.50}{100}\) × 106.5 = Rs. 2.66
The above calculation is based on the assumption that these securities have been purchased at face value.

Question 3.
Based on the following information; determine the NAV of a regular income scheme on per unit basis:

	Rs. in Crores
Listed shares at Cost (ex-dividend) Cash in handBonds and debentures at cost Of these, bonds not listed and quoted Other fixed interest securities at cost	20 1.23 4.3 1 4.5 0 8
Amount payable on shares Expenditure accrued Number of units (Rs. 10 face value)	6.32 0.75 20 lacs
Current realizable value of fixed income
Securities or race value ot Rs. 100 The listed shares were purchased when Index was	106.5 1,000
Present index is	2,300
Value of listed bonds and debentures at NAV date	8

There has been a diminution of 20% in unlisted bonds and debentures other fixed interest securities are at cost. [May 2010] [6 Marks]
Answer:

	Rs. in crores
Market Value of Portfolio [Working Note-1]	59.30
(+) Closing cash in hand	1.23
(+) Dividend Accrued	0.80
Total Closing Assets	61.33
(-) Payable on shares	(6.32)
(-) Expenditure incurred	(0.75)
Closing Net Assets	54.26

NAV per unit = \(\frac{\text { Closing Net Assets }}{\text { Number of Units }}=\frac{\text { Rs. } 54.26 \text { crores }}{20 \text { Lakh Units }}\)
= \(\frac{\text { Rs. } 5426 \text { Lakhs }}{20 \text { Lakh Units }}\) = Rs. 271.30 per unit

Working Note-1 Calculation of Market Value of Portfolio

Particulars	Workings	Rs. in crores
1. Listed Shares	(20 × 2300)/1000	46.00
2. Unlisted Bonds (Unquoted)	(1 – 20%)	0.80
3. Listed Bonds & Debentures	(Given value)	8.00
4. Other Fixed Interest Securities	(At cost)	4.50
		59.30

Question 4.
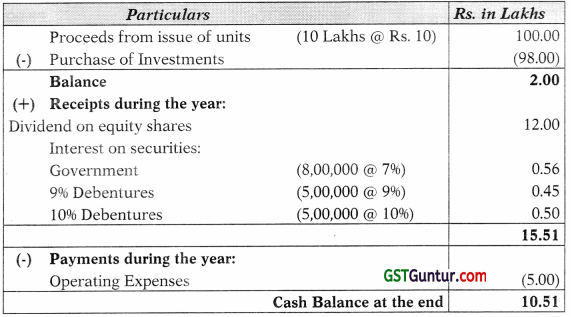
A mutual fund made an issue of 10,00,000 units of Rs. 10 each on January 01, 2008. No entry load was charged. It made the following investments:

50,000 Equity shares of Rs. 100 each @ Rs. 160	Rs. 80,00,000
7% Government Securities	8,00,000
9% Debentures (Unlisted)	5,00,000
10% Debentures (Listed)	5,00,000
	98,00,000

During the year, dividends of Rs. 12,00,000 were received on equity shares, Interest on all types of debt securities was received as and when due. At the end of the year equity shares and 10% debentures are quoted at 175% and 90% respectively. Other investments are at par.
Find out the Net Asset Value (NAV) per unit given that operating expenses paid during the year amounted to Rs. 5,00,000. Also find out the NAV, if the Mutual fund had distributed a dividend of Rs. 0.80 per unit during the year to the unit holders. [Nov. 2009] [8 Marks]
Answer:
(a) Computation of NAV, when dividend is not paid:

	Rs.
Market Value of Portfolio [Working Note-1] (+) Closing cash in hand [Working Note-2] (+) Accrued Income Total Closing Assets (-) Accrued Expenses (-) Other Liabilities	105,00,000 10,51,000 Nil 115,51,000 Nil Nil
Closing Net Assets	115,51,000

NAV per unit = \(\frac{\text { Closing Net Assets }}{\text { Number of Units }}=\frac{\text { Rs. } 115,51,000}{10,00,000 \text { Units }}\)
= Rs. 11.55 per unit

(b) NAV, when dividend is paid:
NAV per unit = \(\frac{\text { Rs. } 115,51,000 \text { minus }(10,00,000 \times 0.80)}{10,00,000 \text { Units }}\) = Rs. 10.75 per unit

Working Note – 1 Calculation of Market Value of Investments

Particulars	Workings	Rs.
1. Equity Shares (Quoted at 175% i.e. Rs. 175)	50,000 @ Rs. 175	87,50,000
2. 10% Debentures (Quoted at 90%)	5,00,000 @ 90%	4,50,000
3. 7% Government Securities		8,00,000
4. 9% Unlisted Debentures		5,00,000
Market Value of Investments		1,05,00,000

Working Note – 2 Calculation of cash balance at the end of year

Question 5.
Based on the following data, estimate the Net Asset Value (NAV) on per unit basis of a Regular Income Scheme of a Mutual Fund:

	Rs. (in lakhs)
Listed Equity shares at cost (ex-dividend)	40.00
Cash in hand	2.76
Bonds & Debentures at cost	8.96
Of these, Bonds not listed & not quoted	2.50
Other fixed interest securities at cost	9.75
Dividend accrued	1.95
Amount payable on shares	13.54
Expenditure accrued	1.76

Additional Information:
(1) Current realizable value of fixed income securities of face value of Rs. 100 is Rs. 96.50.
(2) Number of Units (Rs. 10 face value each): 2,75,000
(3) All the listed equity shares were purchased at a time when market portfolio index was 12,500. On NAV date, the market portfolio index is at 19,975.
(4) There has been a diminution of 15% in unlisted bonds and debentures valuation.
(5) Listed bonds and debentures carry a market value of Rs. 7.5 lakhs, on NAV date.
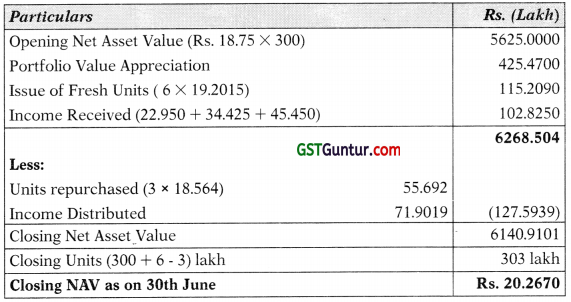
(6) Operating expenses paid during the year amounted to Rs. 2.24 lakhs. Take decimal up to three digits (when expressed in lakhs). [May 2014] [8 Marks]
Answer:
Calculation of Closing Net Assets

	Rs. in crores
Market Value of Portfolio[Working Note-1]	82.954
(+) Closing cash in hand	2.760
(+) Dividend Accrued	1.950
Total Closing Assets	87.664
(-) Payable on shares	(13.54)
(-) Expenditure incurred	(1.76)
Closing Net Assets	72.364

NAV per unit = \(\frac{\text { Closing Net Assets }}{\text { Number of Units }}=\frac{\text { Rs. } 72.364 \text { crores }}{2,75,000 \text { Units }}\)
= \(\frac{\text { Rs. } 72.364 \text { Lakhs }}{2.75 \text { Lakh Units }}\) = Rs. 26.3142 per unit

Working Note-1 Calculation of Market Value of Portfolio:

Particulars	Workings	Rs. in crores
Listed Shares	(40 × 19975)/12500	63.920
Unlisted Bonds (Unquoted)	(2.5 – 15%)	2.125
Listed Bonds & Debentures	(Given value)	7.500
Other Fixed Interest Securities	(9.75 × 96.50)/100	9.409
		82.954

Tutorial Note:
(1) The information regarding operating expenses paid has no use since closing cash as well as closing accrued expenses are given.
(2) It has been assumed that the other fixed interest securities have been acquired at their face value.

Question 6.
A Mutual Fund Co. has the following assets under it on the close of business as on :

Company	No. of Shares	1st February 2012 Market price per share (Rs.)	2nd February 2012 Market price per share (Rs.)
L Ltd.	20,000	20.00	20.50
M Ltd.	30,000	312.40	360.00
N Ltd.	20,000	361.20	383.10
P Ltd.	60,000	505.10	503.90

Total No. of Units 6,00,000
(i) Calculating Net Assets Value (NAV) of the Fund as on 1st February, 2012.
(ii) Following information is given:
Assuming one Mr. A, submits a Cheque of Rs. 30,00,000 to the Mutual Fund and the Fund manager of this company purchases 8,000 shares of M Ltd; and the balance amount is held in Bank. In such a case, what would be the position of the Fund?
(iii) Find new NAV of the Fund as on 2nd February 2012. [May 2012] [8 Marks]
Answer:
(i) NAV of the Fund as on 1st February, 2012

Company	No. of Shares	Market Price	Amount (Rs.)
L Ltd.	20,000	20.00	4,00,000
M Ltd.	30,000	312.40	93,72,000
N Ltd.	20,000	361.20	72,24,000
P Ltd.	60,000	505.10	3,03,06,000
			4,73,02,000

NAV = \(\frac{\text { Rs. } 4,73,02,000}{6,00,000}\) = Rs. 78. 84 (rounded Off)

(ii) The revised position of fund after receipt of Cheque from Mr. A:

Company	No. of Shares	Market Price	Amount (Rs.)
L Ltd.	20,000	20.00	4,00,000
M Ltd.	38,000	312.40	1,18,71,200
N Ltd.	20,000	361.20	72,24,000
P Ltd.	60,000	505.10	3,03,06,000
Cash			5,00,800
			5,03,02,000

Cash Balance = 30 Lakhs – (8,000 × 312.40) = Rs. 5,00,800
No. of units of fund = 6,00,000 + \(\frac{R s .30,00,000}{78.84}\) = 6,38,053

(iii) On 2nd February 2012, the NAV of fund will be as follows:

Shares	No. of Shares	Price (2nd Feb.)	Amount (Rs.)
L Ltd.	20,000	20.50	4,10,000
M Ltd.	38,000	360.00	1,36,80,000
N Ltd.	20,000	383.10	76,62,000
P Ltd.	60,000	503.90	3,02,34,000
Cash			5,00,800
			5,24,86,800

NAV as on 2nd February 2012 = \(\frac{R s .5,24,86,800}{6,38,053}\) = Rs. 82.26 per unit
Assumption: It has been assumed that the cheque of Rs. 30 lakhs has been realised on 1st February itself and the fund manager has purchased the units on the same day.

Question 7.
The following information is extracted from Steady Mutual Fund’s Scheme:

Asset Value at the beginning of the month	Rs. 65.78
Annualized return	15%
Distributions made in the nature of Income (per unit)	Re. 0.50
Distributions made in the nature of Capital gain (per unit)	Re. 0.32

You are required to:
1. Calculate the month end net asset value of the mutual fund scheme (limit ^our answers to two decimals).
2. Provide a brief comment on the month end NAV. [Nov. 2012] [5 Marks]
Answer:
1. Calculation of NAV at the end of month:
r = \(\frac{\left(\mathrm{NAV}_{\mathrm{t}}-\mathrm{NAV}_{\mathrm{t-1}}\right)+\mathrm{I}_{\mathrm{t}}+\mathrm{CG}_{\mathrm{t}}}{\mathrm{NAV}}\)
NAV_t = Net Asset Value at time period t
NAV_t-1 = Net Asset Value at time period t-1
I_t = Income at time period t
CG_t = Capital Gain distribution at time prd. t
Given Annual Return = 15%
Monthly Return (r) = 1.25%
Income (I t) = Re. 0.50
Capital Gain (CG t) = Re. 0.32
NAV_t-1 = Rs. 65.78
0 0125 = \(\frac{\left(\mathrm{NAV}_{\mathrm{t}}-\text { Rs. } 65.78\right)+\text { Re. } 0.50+\text { Re. } 0.32}{\text { Rs. } 65.78}\)
0. 82 = NAV_t – Rs. 64.96
NAV_t = Rs. 65.78 2.
2. There is no change in NAV.

Question 8.
A mutual fund that had a net asset value of Rs. 20 at the beginning of the month made income and capital gain distribution of Re. 0.0375 and Re. 0.03 per share respectively during the month, and then ended the month with a net asset value of Rs. 20.06. Calculate monthly return. [May 2010] [5 Marks]
Answer:

	Rs. Unit
Increase in NAV: [NAVt – NAVt-1] i.e. (Rs. 20.06 – Rs. 20.00)	0.0600
Dividend received [It]	0.0375
Capital gain distribution [CGt]	0.0300
Total Return during Holding period	0.1275

Monthly Return on investment = \(\frac{0.1275}{20}\) x 100 = 0.6375%
Alternative Solution:
r = \(=\left[\frac{\left(N A V_t-N A V_{t-1}\right)+I_t+C G_t}{N A V_{t-1}}\right]\)
Where
R= Return on the mutual fund
NAV_t = Net Assets Value at time period t
NAV_t-1 = Net Assets Value at time period t-1
It= income at time period t
CG_t = Capital Gain distribution at time period t
r = \(\left[\frac{(20.06-20)+0.0375+0.03}{20}\right]\) = 0.006375 or 0.6375%

Question 9.
A mutual fund that had a net asset value of Rs. 16 at the beginning of the month made income and capital gain distribution of Re. 0.04 and Re. 0.03 per share respectively during the month, and then ended the month with a net asset value of Rs. 16.08. Calculate monthly and annual rate of return. [June 2009] [4 Marks]
Answer:

	Rs. Unit
Increase in NPV: [NAVt – NAVt-1] ie. (Rs. 16.08 – Rs. 16)	0.08
Dividend received [It]	0.04
Capital gain distribution [CGt]	0.03
Total Return during Holding period (Month)	0.15

Monthly Return on investment = \(\frac{0.15}{16}\) × 100 = 0.9375%
Annual Rate of Return = \(\frac{0.9375}{1}\) × 12 = 11.25%

Alternative Solution:
r = \(\left[\frac{\left(N A V_t-N A V_{t-1}\right)+I_t+G_t}{N A V_{t-1}}\right]\)
Monthly Return (r) = \(\left[\frac{(16.08-16)+0.04+0.03}{16}\right]\) = 0.009375 or 0.9375%
Annual Rate of Return = \(\frac{0.9375}{1}\) × 12 = 11.25%

Question 10.
An investor purchased 300 units of Mutual Fund at Rs. 12.25 per unit on 31st December, 2009. As on 31st December, 2010 he has received Rs. 1.25 as dividend and Re. 1.00 as capital gains distribution per unit.
Required:
(i) The return on the investment if the NAV as on 31st December, 2010 is Rs. 13.00.
(ii) The return on the investment as on 31st December, 2010 if all dividends
and capital gains distributions are reinvested into additional units of the fund at Rs. 12.50 per unit. [May 2011] [8 Marks]
Answer:
(i) Calculation of Holding Period Return

	Rs./Unit
Increase in NPV: [NAVt – NAVt-1] i.e. (Rs. 13.00 – Rs. 12.25)	0.75
Dividend received[It]	1.25
Capital gain distribution[CGt]	1.00
Total Return during Holding period	3.00

Return on investment = \(\frac{3.00}{12.25}\) × 100
= 24.49% p.a. [Since the holding period is 1 year]

(ii) When all dividends and capital gains distributions are reinvested into additional units of the Fund:

Particulars	Calculations	Result
Dividends and Capital Gains per unit	1.25 + 1.00	Rs. 2.25 per unit
Total amount reinvested from 300 units	Rs. 2.25 × 300	Rs. 675
Reinvestment unit Price		Rs. 12.50
Additional units added	Rs. 675/12.50	54 Units
Value of 354 units at the end of the year	354 × 13	Rs. 4,602
Initial Investment	300 × 12.25	Rs. 3,675

Holding Period Return = \(\frac{\text { Value of closing units }- \text { Initial Investment }}{\text { Initial Investment }}\)
\(\frac{R s .4,602-3,675}{3,675}=\frac{R s .927}{3,675}\) = 25.22%

Question 11.
Orange purchased 200 units of Oxygen Mutual Fund at Rs. 45 per unit on 31st December, 2009. In 2010, he received Re.1.00 as dividend per unit and a capital gains distribution of Rs. 2 per unit.
Required:
(i) Calculate the return for the period of one year assuming that the NAV as on 31st December 2010 was Rs. 48 per unit.
(ii) Calculate the return for the period of one year assuming that the NAV as on 31st December 2010 was Rs. 48 per unit and all dividends and capital gains distributions have been reinvested at an average price of Rs. 46.00 per unit. Ignore taxation. [Nov. 2011] [5 Marks]
Answer:
(i) Calculation of Holding Period Return

	Rs./Unit
Increase in NPV: [NAVt NAVt-1] ie. (Rs. 48 – 45)	3.00
Dividend received [It]	1.00
Capital gain distribution [CGt]	2.00
Total Return during Holding period	6.00

Return on investment = \(\frac{6.00}{45}\) × 100
= 13.3396 p.a. [Since the holding period is 1 year]

(ii) When all dividends and capital gains distributions are reinvested into additional units of the Fund:

Particulars	Calculations	Result
Dividends and Capital Gains per unit	1.00 + 2.00	Rs. 3.00 per unit
Total amount reinvested from 200 units	Rs. 3.00 × 200	Rs. 600
Reinvestment unit Price		Rs. 46
Additional units added	Rs. 600/46	13.04 Units
Value of 213.04 units at the year end	213.04 × 48	Rs. 10,225.92
Initial Investment	200 × 45	Rs. 9,000

Holding Period Return = \(=\frac{\text { Value of closing units – Initial Investment }}{\text { Initial Investment }}\)
= \(\frac{R s \cdot 10,225.92-9,000}{9,000}=\frac{R s \cdot 1,225 \cdot 92}{R s .9,000}\) × 100 = 13.62%

Question 12.
SBI mutual fund has a NAV of Rs. 8.50 at the beginning of the year. At the end of the year NAV increases to Rs. 9.10. Meanwhile fund distributes Re, 0.90 as dividend and Re. 0.75 as capital gains.
(i) What is the fund’s return during the year?
(ii) Had these distributions been reinvested at an average NAV of Rs. 8.75 assuming 200 units was purchased originally, what is the return? [Nov. 2017] [5 Marks]
Answer:
(i) Calculation of Holding Period Return

	Rs. Unit
Increase in NPV: [NAVt NAVt-1] ie. (Rs. 9.10-8.50)	0.60
Dividend received [It]	0.90
Capital gain distribution [CGt]	0.75
Total Return during Holding period	2.25

Return on investment = \(\frac{2.25}{8.50}\) × 100
= 26.47% p.a. [Since the holding period is 1 year]

(ii) When all dividends and capital gains distributions are reinvested into additional units of the Fund:

Particulars	Calculations	Result
Dividends and Capital Gains per unit	0.90 + 0.75	Rs. 1.65 per unit
Totai amount reinvested from 200 units	Rs. 1.65 × 200	Rs. 330
Reinvestment unit Price		Rs. 8.75
Additional units added	Rs. 330/8.75	37.71 Units
Value of 237.71 units at the year end	237.71 × 9.10	Rs. 2,163.16
Initial Investment	200 × 8.50	Rs. 1,700

Holding Period Return = \(\frac{\text { Value of closing units – Initial Investment }}{\text { Initial Investment }}\)
= \(\frac{R s \cdot 2,163.16-1,700}{1,700}\) × 100 = \(\frac{R s .463 .16}{R s .1,700}\) × 100 = 27.25%

Question 13.
A mutual fund having 300 units has shown its NAV of Rs. 8.75 and Rs. 9.45 at the beginning and at the end of the year respectively. The Mutual fund has given two Options to the Investors:
(i) Get dividend of Re. 0.75 per unit and capital gain of Re. 0.60 per unit, or
(ii) These distributions are to be reinvested at an average NAV of Rs. 8.65 per unit.
What difference would it make in term of returns available and which option is preferable by the investors? [Nov. 2018] [8 Marks]
Answer:
Option 1: When Dividend and Capital Gain are paid Returns for the year (on per Unit Basis)

Change in Price (9.45 – 8.75)	0.70
Dividend Received	0.75
Capital Gain	0.60
Total Returns in holding period (one year)	₹ 2.05

Holding Period Reward = \(\frac{2.05}{8.75}\) × 100 = 23.43%
Alternatively:

Option 2: When Dividend and Capital Gain are reinvested

Dividend per unit	0.75
Capital Gain per unit	0.60
	1.35

Total Received for 300 units = 1.35 × 300 = t 405
Additional Units Acquired = \(\frac{405}{8.65}\) = 46.82 units
Total units = 300 + 46.82 = 346.82 units

	Beginning of Year	End of Year
Units held	300	346.82
NAV Per Unit	₹ 8.75	₹ 9.45
Total value	₹ 2,625	₹ 3277.45

Holding Period Reward = \(\frac{3,277.45-2,625}{2,625}\) × 100 = 24.85%
Conclusion: Since the Holding Period Reward is more in terms of percentage in option-II (Reinvestment of distributions), the option II is preferable.

Question 14.
The following information is extracted from Steady Mutual Fund Scheme:

Asset value at the beginning of the month	Rs. 65.78
Annualised Return	15%
Distribution made in the nature of the income (Per Unit)	0.50
Distribution made in the nature of the Capital Gain (Per Unit)	0.32

(i) Calculate the month end Net Assets Value of the mutual fund scheme (Limit your answer to two decimal).
(ii) Provide a brief comment on the month end NAV. [Nov. 2012] [5 Marks]
Answer:
(i) Calculation of NAV at the end of the month
r = \(\left[\frac{\left(N A V_t-N A V_{t-1}\right)+I_t+G_{\mathrm{I}}}{N A V_{t-1}}\right]\)
Where
R= 15% p.a. = 1.25% per month
NAV_t =?
NAV_t-1 = Rs. 65.78
I = Rs. 0.50
G_t = Rs. 0.32
0.00125 = \(\left[\frac{\left(\mathrm{NAV}_{\mathrm{t}}-65.78\right)+0.50+0.32}{65.78}\right]\)

On solving the above equation, we get NAV_t = Rs. 65.78
(ii) Comment on month end NAV
There is no change in the value of NAV, as the entire income and gain has been distributed.

Question 15.
A Mutual Fund having 300 units has shown its NAV of Rs. 8.75 and Rs. 9.45 at the beginning and at the end of the year respectively. The Mutual Fund has given two options:
(i) Pay Re. 0.75 per unit as dividend and Re. 0.60 per unit as a capital gain, or
(ii) These distributions are to be reinvested at an average NAV of Rs. 8.65 per unit.
What difference it would make in terms of return available and which option is preferable? [May 2006] [6 Marks]
Answer:
Calculation of Holding Period Return under OPTION I [Income Plan]

	Rs. Unit
Increase in NPV: [NAVt NAVt-1] ie. (Rs. 9.45 – 8.75)	0.70
Dividend received [It]	0.75
Capital gain distribution [CGt]	0.60
Total Return during Holding period	2.05

Return on investment = \(\frac{2.05}{8.75}\) × 100
= 23.43% p.a. [Since the holding period is 1 year]

Under option II, all dividends and capital gains distributions are reinvested into additional units of the Fund @ Rs. 8.65 per unit.

Particulars	Calculations	Result
Dividends and Capital Gains per unit	0.75 + 0.60	Rs. 1.35 per unit
Total amount reinvested from 300 units	Rs. 1.35 × 300	Rs. 405.00
Reinvestment unit Price		Rs. 8.65
Additional units added	Rs. 405/8.65	46.82 Units
Total units at the end after reinvestment	300 + 46.82	346.82
Value of 346.82 units at the year end	346.82 × 9.45	Rs. 3,277.45
Initial Investment	300 × 8.75	Rs. 2,625.00

Holding Period Return = \(\frac{\text { Value of closing units }- \text { Initial Investment }}{\text { Initial Investment }}\)
= \(\frac{R s .3,277.45-2,625.00}{2,625.00}\) × 100 = \(\frac{R s .652 .45}{R s .2,625.00}\) × 10 = 24.85%
Comment: Since, the Holding Period Reward (in terms of percentage) is more under reinvestment plan, the option II is preferable.

Question 16.
A has invested in three Mutual Fund Schemes as per details below:

	MF-A	MF-B	MFC
Date of Investment	1-12-2009	1-1-2010	1-3-2010
Amount of Investment (Rs.)	50,000	1,00,000	50,000
Net Assets value at entry date	Rs. 10.50	Rs. 10.00	Rs. 10.00
Dividend received up to 31-3-2010	Rs. 950	Rs. 1,500	Nil
Net Asset value as at March 31, 2010	Rs. 10.40	Rs. 10.10	Rs. 9.80

Required:
What is the effective yield on per annum basis in respect of each of the above three schemes to Mr. A up to 31-3-2010? [Nov. 2004] [6 Marks]
Answer:
Calculation of units purchased

Particulars	MFA	MFB	MFC
Amount of Investment (Rs.) (A)	50,000	1,00,000	50,000
NAV at entry date (B)	10.50	10	10
No. of units (A)/(B)	4,761.905	10,000	5.000

Calculation of effective yield

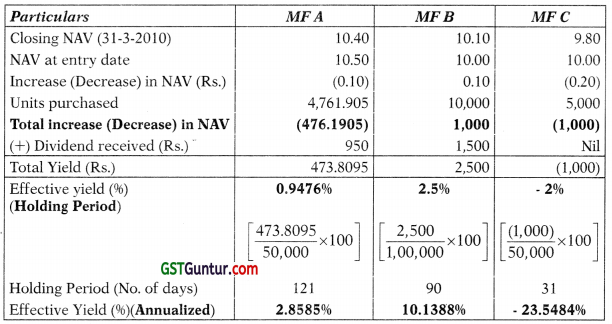
Tutorial Note: While calculating number of days, the date of investment is taken into account.

Question 17.
Mr. Sinha has invested in three Mutual Fund Schemes as per details below: [Nov. 2009] [6 Marks]

	MF-A	MF-B	MFC
Date of Investment	1-12-2008	1-1-2009	1-3-2009
Amount of Investment (Rs.)	5,00,000	1,00,000	50,000
Net Assets value at entry date	Rs. 10.50	Rs. 10.00	Rs. 10.00
Dividend received up to 31-3-2009	Rs. 9,500	Rs. 1,500	Nil
Net Asset value as at March 31, 2009	Rs. 10.40	Rs. 10.10	Rs. 9.80

You are required to calculate the effective yield on per annum basis in respect of each of the three schemes to Mr. Sinha up to 31-3-2009?
Answer:
Calculation of units purchased

Calculation of effective yield

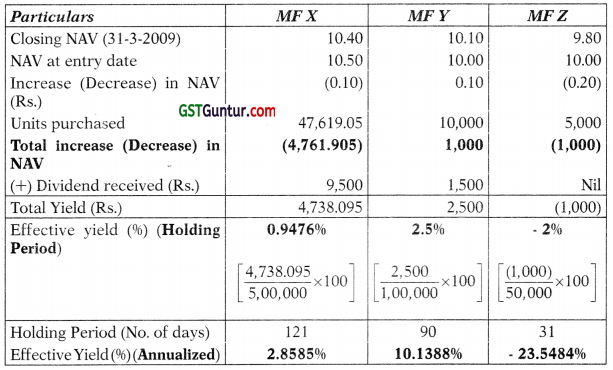
Tutorial Note: While calculating number of days, the date of investment is taken into account.

Question 18.
TUV Ltd. has invested in three Mutual Fund schemes as per the details given below:

	Scheme X	Scheme Y	Scheme Z
Date of Investment	1-10-2014	1-1-2015	1-3-2015
Amount of Investment (Rs.)	15,00,000	7,50,000	2,50,000
Net Assets value at entry date	Rs. 12.50	Rs. 36.25	Rs. 27.75
Dividend received up to 31-3-2015	Rs. 45,000	Rs. 12,500	Nil
Net Asset value as at March 31, 2015	Rs. 12.25	Rs. 36.45	Rs. 27.55

What will be the effective yield (per annum basis) for each of the above three schemes upto 31st March 2015?
Answer:
Calculation of units purchased

Particulars	MFX(Rs.)	MF Y (Rs. )	MFZ (Rs.)
Amount of Investment (A)	15,00,000	7,50,000	2,50,000
NAV at entry date (B)	12.50	36.25	27.75
No. of units (A)/(B)	1,20,000	20,689.66	9,009

Calculation of effective yield

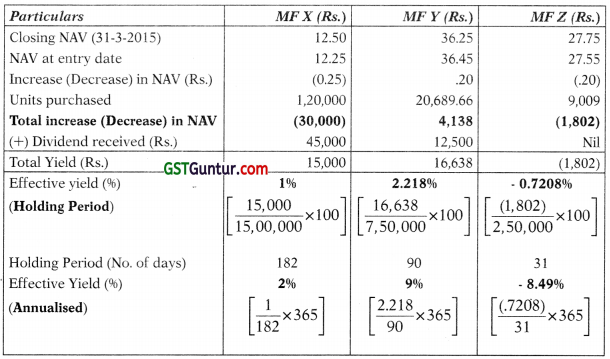
Tutorial Note: While calculating number of days, the date of investment is taken into account.

Question 19.
Mr. A has invested in three Mutual Fund (MF) schemes as per the details given below:

Particulars	MF ‘A’	MFB’	MF‘C’
Date of Investment	01-11-2015	01-02-2016	01-03-2016
Amount of Investment (Rs.)	1,00,000	2,00,000	2,00,000
Net Asset Value at entry date (Rs.)	10.30	10.00	10.10
Dividend Received up to 31-3-2016 (Rs.)	2,850	4,500	Nil
NAV as on 31-3-2016 (Rs.)	10.25	10.15	10.00

Assume 1 year = 365 days. Show the amount of rupees up to two decimal points.
You are required to find out the effective yield (up to three decimal points) on per annum basis in respect of each of the above three Mutual Fund (MF) schemes up to 31-3-2016. [Nov. 2016] [5 Marks]
Answer:
Calculation of units purchased

Calculation of effective yield

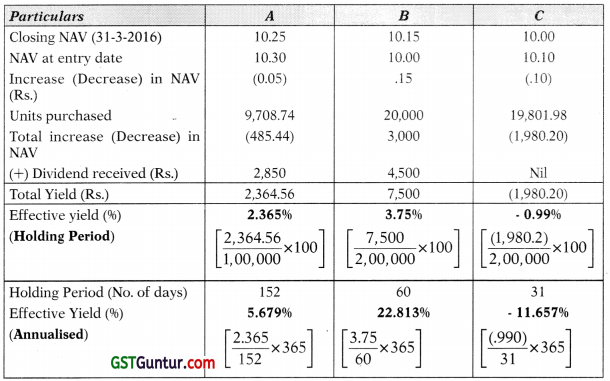
Tutorial Note: While calculating number of days, the date of investment is taken into account.

Question 20.
Mr. Suhail has invested in three Mutual Fund Schemes as given below:

Particulars	Scheme A Rs.	Scheme B Rs.	Scheme C Rs.
Date of investment	1-4-2011	1-5-2011	1-7-2011
Amount of investment	12,00,000	4,00,000	2,50,000
Net Asset Value at entry date	10.25	10.15	10.00
Dividend received up to 31-7-2011	23,000	6,000	Nil
NAV as at 31-7-2011	10.20	10.25	9.90

You are required to calculate the effective yield on per annum basis in respect of each of the three Schemes to Mr. Suhail up to 31-7-2011.
Take one year = 365 days.
Show calculations up to two decimal points. [May 2013] [10 Marks]
Answer:
Calculation of units purchased

Particulars	A	B	C
Amount of Investment (x)	12,00,000	4,00,000	2,50,000
NAV at entry date (y)	10.25	10.15	10.00
No. of units (x)/(y)	1,17,073.17	39,408.87	25,000

Calculation of effective yield

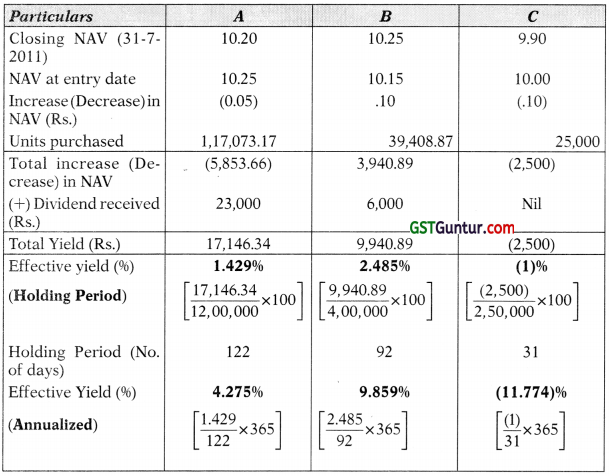
Tutorial Note: While calculating number of days, the date of investment is taken into account.

Question 21.
Ramesh Goyal has invested in three Mutual Funds. From the details given below, find out effective yield on per annum basis in respect of each of the schemes to Ramesh Goyal up to 31.03.2012.

Mutual Fund	X	Y	z
Date of investment	01.12.2011	01.01.2012	01.03.2012
Amount of investment (Rs.)	1,00,000	2,00,000	1,00,000
NAV at the date of investment (Rs.)	10.50	10.00	10.00
Dividend receipt upto 31.03.2012 (Rs.)	1,900	3,000	Nil
NAV as on 31.03,2012 (Rs.)	10.40	10.10	9.80

Answer:
Computation of Net Value Added during the year ended 31.03.2012

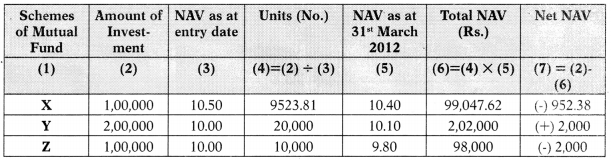
Effective yield in %

Question 22.
Mr. Y has invested in three Mutual Fund (MF) schemes as per the following details:

Particulars	MF‘X’	MF‘Y’	MF‘Z’
Amount of Investment (Rs.)	2,00,000	4,00,000	2,00,000
Net Asset Value at the time of purchase (Rs.)	10.30	10.10	10.00
Dividend Received up to 31-3-2018 (Rs.)	6,000	Nil	5,000
NAV as on 31-3-2018 (Rs.)	10.25	10.00	10.20
Effective Yield per annum as on 31-3-2018 (%)	9.66	-11.66	24.15

Assume 1 year = 365 days.
Mr. Y has misplaced the documents of his investment. Help him in finding the date of his original investment after ascertaining the following:
(i) Number of units in each scheme
(ii) Total NAV
(iii) Total Yield and
(iv) Number of days investment held [May 2018] [5 Marks]
Answer:
(i) Calculation of Number of Units in each Scheme

(ii) Calculation of Total NAV on 31.03.2018

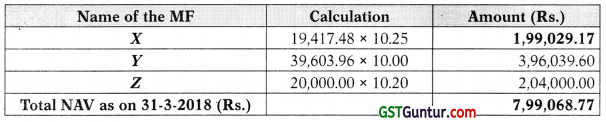
(iii) Total Yield

Total Yield = \(\frac{10,068.77}{8,00,000}\) × 100 = 1.2586%

(iv) Determination of Number of days the investment is held:

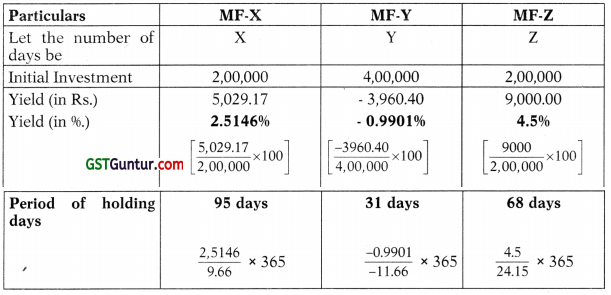
Tutorial Note: While calculating number of days, the date of investment is taken into account.

Question 23.
Mr. A can earn a return of 16% by investing in equity shares on his own. Now, he is considering a recently announced equity based mutual fund scheme in which initial expenses are 5.5% and annual recurring expenses are 1.5%. How much should the Mutual Fund earn to provide Mr. A return of 16%? [Nov. 2003] [4 Marks]
Answer:
r₁ = Personal earnings of Mr. A = 16%
r₂ = Mutual Funds earnings
r₂ = \(\frac{r_1}{1-\text { initial } \exp \cdot(\%)}\) + recuring exp.(%)

The rate of return the mutual fund should earn (ie. r₂);
r₂ = \(\frac{16 \%}{1-0.055}\) + 1.5% = 16.93 + 1.5 = 18.43%

Question 24.
Mr. X earns 10% on his investments in equity shares. He is considering a recently floated scheme of a Mutual Fund where the initial expenses are 6% and annual recurring expenses are expected to be 2%. How much the Mutual Fund scheme should earn to provide a return of 10% to Mr. X? [June 2009] [2 Marks]
Answer:
r₁ = Personal earnings of Mr. X
r₂ = Mutual Funds earnings
r₂ = \(\frac{r_1}{1-\text { initial } \exp (\%)}\) + recuring exp.(%)
The rate of return the mutual fund should earn (ie. r₂);
r₂ = \(\frac{10 \%}{1-0.06}\) + 2% = 10.64 + 2 = 12.64%

Question 25.
“Mr. Alex, a practicing Chartered Accountant, can earn a return of 15 per cent by investing in equity shares on his own. He is considering a recently announced equity based mutual fund scheme in which initial expenses are 6 per cent and annual recurring expenses are 2 per cent.
(i) How much should the mutual fund earn to provide Mr. Alex a return of 15 per cent per annum ?
(ii) Mr. Alex’s current Annual Professional Income is Rs. 40 Lakhs. His portfolio value is Rs. 50 Lakhs and now he is spending 10% of his time to manage his portfolio. If he spends this time on profession, his profes-sional income will go up in same proportion. He is thinking to invest his entire portfolio into a Multieap Fund, assuming the fund’s NAV will grow at 13% per annum (including dividend).
You are requested to advise Mr. Alex, whether he can invest the portfolio into Multicap Funds ? If so, what is the net financial benefit ? [Nov. 2019 Old Syllabus] [8 Marks]
Answer:
(i) r₁ = Personal earnings of Mr. X
r₂ = Mutual Funds earnings
r₂ = \(\frac{r_1}{1-\text { initial } \exp (\%)}\) + recuring exp.(%)
The rate of return the mutual fund should earn (i.e. r₂);
r₂ = \(\frac{15 \%}{1-0.06}\) + 2.0% = 15.96 + 2 = 17.96%

(ii) Calculation of Return when 100% time is devoted to profession:
Current Income of Mr. Alex = Rs. 40 Lakh He spends 90% time in profession.
Increase in Income by investing 10% remaining time = \(\frac{40}{90}\) × 10
= Rs. 4.44 Lakhs
Total Income from profession (100% time) = Rs. 44.44 Lakhs

Source	90% time to Profession (Existing)	100% time to Profession (Proposed)
Professional Income	Rs. 40 Lakhs	Rs. 44.44 Lakhs
Return from investment in Equity	Rs. 50 Lakhs × 15% = Rs. 7.50 Lakhs	Nil
Return from investment in Mutual Fund	Nil	Rs. 50 Lakhs × 13% = Rs. 6.50 Lakhs
Total	47.5 Lakhs	50.94 Lakhs

∴ Increase in Income (50.94 – 47.5) = Rs. 3.44 Lacs
Therefore, Mr. Alex is advised to invest the portfolio into Multicap Funds and devotes 100% time to his profession.

Question 26.
The unit price of Equity Linked Savings Scheme (ELSS) of a mutual fund is Rs. 10. The public offer price (POP) of the unit is Rs. 10.204 and the redemption price is Rs. 9.80.
Calculate:
(i) Front-end Load
(ii) Back-end Load [May 2018 Old Course] [5 Marks]
Answer:
(i) Calculation of Front-end Load:
Public Offer Price = \(\frac{\text { Net Asset Value }}{1-\text { Front-end load }}\)
10.204 = \(\frac{10}{1-\text { Front-end load }}\)
Therefore,
1 – Front end load = \(\frac{10}{10.204}\) = .9
Front end load = 1 – 0.98 = .02 = 2%

(ii) Calculation of Back-end Load:
Redemption Price = Net Asset Value × (1- Back-end Load)
9.8 = 10 × (1- Back-end Load)
Therefore,
1 – Back end load = \(\frac{9.8}{10}\) = 0.98 10
Back end load = 1- 0.98 = .02 = 2%

Alternative Solution suggested by ICAI
Front End Load = \(\frac{10.204-10.00}{10.00}\) = 0.0204 or 2.04%
Exit Load = \(\frac{10.00-9.80}{10.00}\) = 0.020 or 2.00%

Question 27.
During the year 2017 an investor invested in a mutual fund. The capitai gain and dividend for the year was Rs. 3.00 per unit, which were reinvested at the year-end NAV of Rs. 23.75. The investor had total units of 26,750 as at the end of the year. The NAV had appreciated by 18.75% during the year and there was an entry load of Re. 0.05 at the time when the investment was made.
The investor lost his records and wants to find out the amount of investment made and the entry load in the mutual fund. [Nov. 2018 Old Course] [5 Marks]
Answer:
Calculation of Opening NAV
Closing NAV is Rs. 23.75 and Increase in NAV is 18.75%.
Therefore, if the opening NAV is x, then
x + 0.1875 x = 23.75
x = Rs. 20 Therefore, opening NAV was Rs. 20.

Calculation of Units purchased initially
Let number of units purchased initially = Y
Capital Gain and Dividends distributed = Rs. 3 per unit
Therefore, total Capital Gains = 3Y
Number of new units purchased by re-investment is calculated as follows:
= \(\frac{\text { Capital Gains + Dividends }}{\text { Closing NAV }}=\frac{3 Y}{R s .23 .75}\)
Therefore, total number of units = Y + \(\frac{3 Y}{R s .23 .75}\)
Given total units = 26,750
Y + \(\frac{3 Y}{R s .23 .75}\) = Rs. 23.75
Y = 23,750 units
Original units purchased = 23,750 units
Calculation of Investment made and Entry Load paid
Entry Load = 0.05
Cost Price of each unit at the time of investment = NAV + Entry Load = Rs. 20.00 + 0.05 = 20.05
Total investment = 23,750 Units x Rs. 20.05 = Rs. 4,76,187.50
Entry Load = 23,750 Units × Re. 0.05 = Rs. 1,187.50

Question 28.
On 1-4-2012 ABC Mutual Fund issued 20 lakh units at Rs. 10 per unit. Relevant initial expenses involved were Rs. 12 lakhs. It invested the fund so raised in capital market instruments to build a portfolio of Rs. 185 lakhs. During the month of April 2012 it disposed off some of the instruments costing Rs. 60 lakhs for Rs. 63 lakhs and used the proceeds in purchasing securities for Rs. 56 lakhs. Fund management expenses for the month of April 2012 were Rs. 8 lakhs of which 10% was in arrears. In April 2012 the fund earned dividends amounting to Rs. 2 lakhs and it distributed 80% of the realized earnings. On 30-4-2012 the market value of the portfolio was Rs. 198 lakhs.
Mr. Akash, an investor, subscribed to 100 units on 1-4-2012 and disposed off the same at closing NAV on 30-4-2012. What was his annual rate of earning? [May 2013] [8 Marks]
Answer:
Calculation of Closing Net Assets

	Rs. in Lakhs
Market Value of Portfolio	198.00
(+) Closing cash in hand [Working Note- 1]	0.80
(+) Accrued Income	Nil
Total Closing Assets	198.80
(-) Accrued Expenses	(Nil)
(-) Other Liabilities (Management Expenses)	(0.80)
Closing Net Assets	198.00

NAV per unit = \(\frac{\text { Closing Net Assets }}{\text { Number of Units }}=\frac{\text { Rs. } 198.00 \text { Lakhs }}{20 \text { Lakhs Units }}\) = Rs. 9.90 per unit

Calculation of Holding Period Return (Per Unit)

	Rs.Unit
Increase in NPV: [NAVt – NAVt-1] i.e. (Rs. 10.00 – Rs. 9.90)	(0.10)
Dividend received [It Per Unit [1.60 ÷ 20]	0.08
Capital gain distribution [CGt]	0.12
Total Return during Holding period	0.10

Return on investment (Monthly) = \(\frac{0.10}{10}\) × 100
= 1%
Return on investment (Annualized) = \(\frac{1}{1}\) × 12 = 12% p.a.

Working Note-1
Calculation of cash balance at the end of year

Question 29.
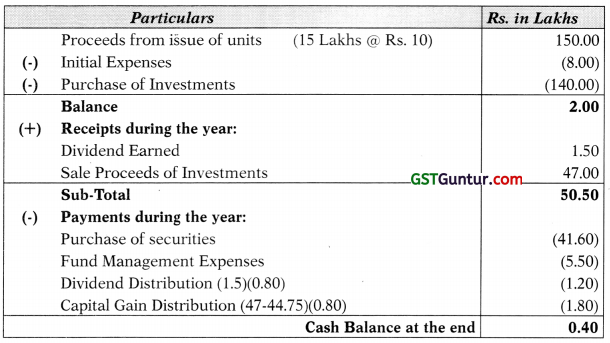
A mutual fund raised Rs. 150 lakhs on April 1, 2018 by issue of 15 lakhs units at Rs. 10 per unit. The fund invested in several capital market instruments to build a portfolio of Rs.140 lakhs. Initial expenses amounted to Rs. 8 lakhs. During the month of April, the funds sold certain instruments costing Rs. 44.75 lakhs for Rs. 47 lakhs and used the proceeds to purchase certain other securities for Rs. 41.6 lakhs. The fund management expenses for the month amounted to Rs. 6 lakh of which Rs. 50,000 was in arrears. The fund earned dividends amounting to Rs. 1.5 lakhs and it distributed 80% of the realized earning. The market value of the portfolio on 30th April, 2018 was Rs. 147.85 lakhs.
An investor subscribed to 1000 units on April 1 and disposed it off at closing NAV on 30th April. Determine his annual rate of earnings. [Nov. 2018] [8 Marks]
Answer:
Calculation of Closing Net Assets

NAV per unit = \(\frac{\text { Closing Net Assets }}{\text { Number of Units }}=\frac{\text { Rs. } 147.75 \text { Lakhs }}{15 \text { Lakhs Units }}\) = Rs. 9.85 per unit

Calculation of Holding Period Return (Per Unit)

	Rs. Unit
Increase in NPV: [NAVt – NAVt-1] i.e. (Rs. 10.00 – Rs. 9.85)	(0.15)
Dividend received [It]	0.08
Capital gain distribution [CGt]	0.12
Total Return during Holding period	0.05

Return on investment (Monthly) = \(\frac{0.05}{10}\) × 100 = 0.5%
Return on investment (Annualized) = 0.5 × 12 = 6.0% p.a.

Working Note-1
Calculation of cash balance at the end of year

Question 30.
The following particulars relating to Vishnu Fund scheme:

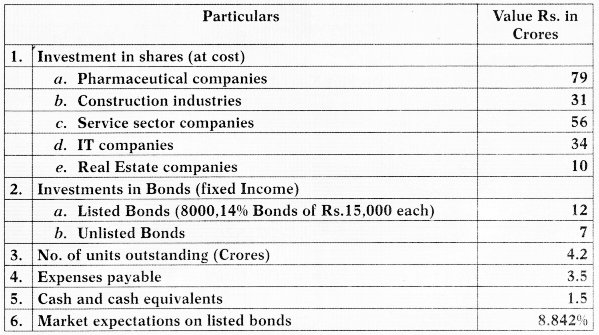
Particulars relating to each sector are as follows:

Sector	Index on date of
	Purchase	Valuation
Pharmaceutical companies	260	465
Construction industries	210	450
Service sector companies	275	480
IT companies	240	495
Real Estate companies	255	410

The fund has incurred the following expenses:

Consultancy and Management fees	Rs. 480 Lakhs
Office Expenses	Rs. 150 Lakhs
Advertisement Expenses	Rs. 38 Lakhs

You are required to calculate the following:
i. Net Asset Value of the fund
ii. Net asset value per unit
iii. If the period of consideration is 2 years, and the fund has distributed Rs. 3 per unit per year as cash dividend, ascertain the Net return (Annualized).
iv. Ascertain the Expenses ratio. [May 2019][5 Marks]
Answer:
(i) Net Asset Value of the Fund

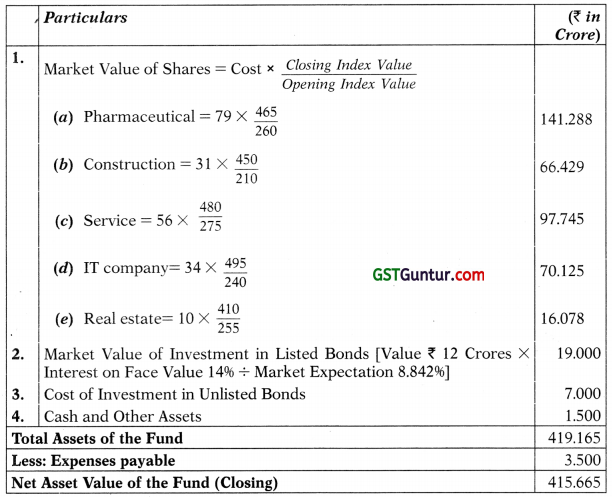
(ii) Net Asset Value per Unit
NAV per Unit = Net Asset Value of the Fund × No. of Units Outstanding
= ₹ 415.665 Crores × 4.2 Crore Units= ₹ 98.97

(iii) Annualized Return on Fund
(a) Computation of Opening NAV

	Particulars	(₹ in Crore)
1.	Investment in shares (at cost)
	(a) Pharmaceutical companies	79
	(b) Construction industries	31
	(c) Service sector companies	56
	(d) IT companies	34
	(e) Real Estate companies	10
	Particulars	(₹ in Crore)
2.	Investments in Bonds (fixed Income)
	(a) Listed Bonds (8000,14% Bonds of Rs. 15,000 each)	12
	(b) Unlisted Bonds	7
Net Asset Value of the Fund (Opening)		229

Note: Cash and Other Assets are not included because they arise out of investments made in the beginning.

(b) Computation of Opening NAVper Unit
NAV per Unit = Net Asset Value of the Fund No. of Units Outstand-ing
= ₹ 229.00 Crores ÷ 4.20 Crore Units
= ₹ 54.52

(c) Computation of Returns per Unit

Capital Appreciation = Closing NAV per Unit – Opening NAV per	44.45
Unit = ₹ 98.97 – 54.52
Cash Dividend = ₹ 3 × 2 Year	6.00
Total Returns	50.45

(d) Computation of Returns in percentage
NAV per Unit = \(\frac{\text { Return }}{\text { Opening NAV }}\) × 100 = \(\frac{50.45}{54.52}\) × 100 = 92.53%
Return p.a. = Total Return/Period = 92.53% ÷ 2 Years = 46.26%

4. Expense Ratio
(a) Total Expense = Management Advisory Fees ₹ 480 Lakhs + Administration Exp. ₹ 38 Lakhs + Office Expenses ₹ 150 Lakhs = ₹ 668 Lakhs

(b) Average Value of Portfolio
= (Opening Net Asset Value + Closing Net Asset Value) ÷ 2
= (₹ 415.665 Crores + ₹ 229 Crores) ÷ 2
= ₹ 644.665 Crores ÷ 2
= ₹ 322.33 Crores

(c) Expense Ratio = Total Expenses ÷ Average Value of Portfolio
= (₹ 6.68 Crores ÷ ₹ 322.33 Crores) × 100
= 2.07%

(d) Expense Per Unit = Total Expenses ÷ No. of Units = ₹ 6.68 Crores ÷ 4.20 Crores = ₹ 1.59 per unit

Question 31.
Mr. X on 1.7.2012, during the initial public offer of a Mutual Fund (MF) invested Rs. 1,00,000 at Face Value of Rs. 10. On 31.3.2013, the MF declared a dividend of 10% when Mr. X calculated that his holding period return was 115%. On 31.3.2014, MF again declared a dividend of 20%. On 31.3.2015, Mr. X redeemed all his investment which had accumulated to 11,296.11 units when his holding period return was 202.17%.
Calculate the NAV as on 31.03.2013, 31.03.2014 and 31.03.2015. [Nov. 2015] [8 Marks]
Answer:
Calculation of NAV as on 31-3-2013

Original Investment	=	Rs. 1,00,000
Yield for 9 months	=	115%
Market Value of Investments (on 31-3-2013)	=	1,00,000+ 115% 2,15,000
Dividend Paid	=	10% of 1,00,000 Rs. 10,000

NAV would stand reduced to the extent of Dividend Payout.
Therefore, NAV (31-3-2013) = \(\frac{\text { Rs. } 2,15,000-\text { Rs. } 10,000}{10,000 \text { Units }}\) = Rs 20 50

Calculation of NAV as on 31-3-2014

Dividend as on 31.3.2014 = 10,487.80 Units × 10 × 0.2 = Rs. 20,975.60
Units after reinvestment of above dividend = 11,296.11 Units
Increase in units due to reinvestment = 11,296.11 – 10,487.80 = 808.31 Units
Additional units purchased on 31-3-2017 = \(\frac{\text { Dividend Received on 31-3-2014 }}{\text { NAV on 31-3-2014 }}\)
808.31 = \(=\frac{\text { Rs. } 20,975.60}{\text { NAV on } 31-3-2014}\)
Therefore, NAV on 31-3-2014 = \(\frac{\text { Rs. } 20,975.60}{808.31}\) = Rs 25.95

Calculation of NAV as on 31-3-2015

Original Investment	=	Rs. 1,00,000
Holding Period Return (1-7-2012 to 31-3-2015)	=	202.17%
Therefore, Value of Investments on 31-3-2015	=	1,00,000 + 202.17%
	=	Rs. 3,02,170
Number of Units held on 31-3-2015	=	11,296.11 Units

Therefore, NAV on 31-3-2015 = \(\frac{\text { Rs. } 3,02,170}{11,296.11 \text { Units }}\) = Rs. 26.75

Question 32.
Mr. X on 1.7.2000, during the initial offer of some Mutual Fund invested in 10,000 units having face value of Rs. 10 for each unit. On 31.3.2001, the dividend operated by the M.F. was 10% and Mr. X found that his annualized yield was 153.33%. On 31.12.2002, 20% dividend was given. On 31.3.2003, Mr. X redeemed all his balance of 11,296.11 units when his annualized yield was 73.52%. What are the NAVs as on 31.3.2001, 31.12.2002 and 31.3.2003? [Nov. 2006] [6 Marks]
Answer:
This question is similar to Q. 30 (came in Nov. 2015) with the only dif-ference that in this question the annualized yield is given, which needs to be converted into holding period yield, in the following manner:
Yield for 9 months = 153.33 × \(\frac{9}{12}\) = 115%.
The rest of the solution is exactly similar to Q. 30 given before this question.

Question 33.
On 01 -07-2010, Mr. X invested Rs. 50,000 at initial offer in Mutual Funds at a face value of Rs. 10 each per unit. On 31-03-2011, a dividend was paid @ 10% and annualized yield was 120%. On 31-3-2012, 20% dividend and capital gain of Re. 0.60 per unit was given. Mr. X redeemed all his 6271.98 units when his annualized yield was 71.50% over the period of holding.
Calculate NAV as on 31-03-2011, 31-03-2012 and 31-03-2013.
For calculations consider a year of 12 months. [Nov. 2013] [5 Marks]
Answer:
Calculation of NAV as on 31-3-2011

Original Investment	=	Rs. 50,000
Annualized Yield	=	120%
Holding Period (1-7-2010 to 31-3-2011)	=	9 Months
Yield for 9 months 120 X 9/12	=	90%
Market Value of Investments (on 31-3-2011)	=	50,000 + 90% = 95,000
Dividend Paid	=	10% of 50,000 = Rs. 5,000

NAV would stand reduced to the extent of Dividend Payout.

Therefore, NAV (31-3-2011) = \(\frac{\text { Rs. } 95,000-\text { Rs. } 5,000}{5,000 \text { Units }}\) = Rs. 18.00

Calculation of NAV as on 31-3-2013

Dividend as on 31.3.2012 = 5,277.78 Units × 10 × 0.2 = Rs. 10,555.56
Units after reinvestment of above dividend 6,271.98 Units
Increase in units dueto reinvestment = 6,271.98 – 5,277.78 = 994.20 Units
Additional units purchased on 3 1-3-2012 = \(\frac{\text { Dividend Received on 31-3-2012 }}{\text { NAV on } 31-3-2012}\)
994.20 = \(\frac{\text { Rs. } 10,555.56}{\mathrm{NAV} \text { on } 31-3-2012}\)
Therefore, NAV on 3 1-3-2012 = \(\frac{\mathrm{Rs} .10,555.56}{994.20}\) = Rs. 10.62

Calculation of NAV as on 31-3-2013

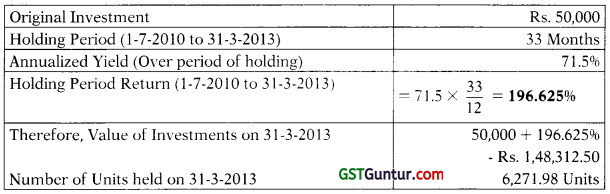
Therefore, NAV on 31-3-2013 = \(\frac{\mathrm{Rs} \cdot 1,48,312.50}{6271.98 \text { Units }}\) = Rs. 23.65

Question 34.
A reputed financial institution of the country floated a mutual fund having a corpus of Rs. 10 crores consisting of 1 crore units of Rs. 10 each. Mr. Vijay invested Rs. 10,000 for 1,000 units of Rs. 10 each on 1st July 2014. For the financial year ended 31st March 2015, the fund declared a dividend of 10% and Mr. Vijay found that his annualized yield from the fund was 153.33%. The mutual fund during the financial year ended 31st March 2016, declared a dividend of 20%. Mr. Vijay has reinvested the entire dividend in acquiring units of this mutual fund at its appropriate NAV. On 31st March 2017 Mr. Vijay redeemed all his balances of 1129.61 units when his annualized yield was 73.52%.
You are required to find out NAV as on 31st March 2015, 31st March 2016 and 31st March 2017. [Nov. 2017] [8 Marks]
Answer:
Calculation of NAV as on 31-3-2015

Original Investment	Rs. 10,000
Annualized Yield	153.33%
Holding Period (1-7-2014 to 31-3-2015)	9 Months
Yield for 9 months 153.33 × 9/12	115%
Market Value of Investments (on 31-3-2015)	10,000 + 115% – Rs. 21,500
Dividend Paid	10% of 10,000 – Rs. 1,000

NAV would stand reduced to the extent of Dividend Payout.
Therefore, NAV (31-3-2015) = \(\frac{\text { Rs. } 21,500-\text { Rs. } 1,000}{1,000 \text { Units }}\) = Rs. 20.50

Calculation of NAV as on 31-3-2016

Dividend as on 31.3.2016 = 1,048.78 Units × 10 × 0.2 = Rs. 2,097.56
Units after reinvestment of above dividend = 1,129.56
Units Increase in units due to reinvestment = 1,129.61 – 1,048.78 = 80.83 Units
Additional units purchased on 31-3-2016 = \(\frac{\text { Dividend Received on 31-3-2016 }}{\text { NAV on 31-3-2016 }}\)
80.83 = \(\frac{\text { Rs. } 2,097.56}{\text { NAV on } 31-3-2016}\)
Therefore, NAV on 31-3-2016 = \(\frac{\text { Rs. 2,097.5 }}{80.83}\) = Rs. 25.95

Calculation of NAV as on 31-3-2017

Therefore, NAV on 31-3-2017 = \(\frac{{Rs} .30,218}{1129.61 \text { Units }}\) = Rs. 26.75

Question 35.
The following are the data on five mutual funds:

Mutual Fund	Return	Standard Deviation	Beta
A	15	7	1.25
B	18	10	0.75
C	14	5	1.40
D	12	6	0.98
E	16	9	1.50

You are required to compute Reward to Volatility Ratio and rank these port-folios using:
(a) Sharpe Method and
(b) Treynor method
Assuming the risk free rate is 6%. [May 2016] [5 Marks]
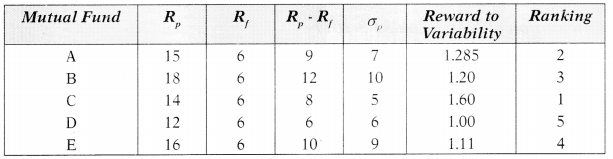
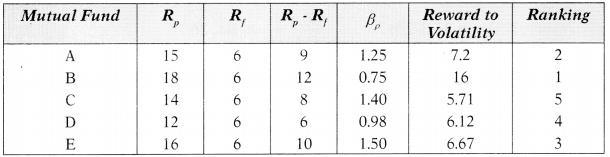
Answer:
Sharpe Ratio (S) = \(\frac{\mathrm{R}_{\mathrm{p}}-\mathrm{R}_{\mathrm{f}}}{\alpha_{\mathrm{p}}}\)
Where
R_p = Return on Fund
R_f = Risk-free rate

Treynor Ratio (T) = \(\frac{\mathrm{R}_{\mathrm{p}}-\mathrm{R}_{\mathrm{f}}}{\beta_p}\)
σ = Standard deviation of Fund
β_r = Beta of Fund
The Sharpe ratio indicates the excess return per unit of total risk. It implies that a higher ratio indicates more returns. Therefore, the mutual fund having highest ratio should be ranked first and so on.

Calculation of Sharpe Ratio (Reward to Variability)

The Treynor ratio indicates the excess return per unit of systematic risk. The higher should be preferred and rank should be given accordingly.

Calculation of Treynor Ratio (Reward to Volatility)

Question 36.
The five portfolios of a mutual fund experienced following result during last 10 years periods:

Portfolio	Average annual re­turn %	Standard deviation	Correlation with the market return
A	20.0	2.3	0.8869
B	17.0	1.8	0.6667
C	18.0	1.6	0.600
D	16.0	1.8	0.867
E	13.5	1.9	0.5437

Market risk (σ_m) : 1.2
Market rate of return : 14.3%
Risk free rate : 10.1%
Beta may be calculated only upto two decimal. Rank the portfolio using JENSEN’S ALPHA method. [May 2017] [8 Marks]
Answer:
The Jensen’s Alpha measures the difference between expected return of the portfolio and the required return as per CAPM model. This difference is called as’alpha. If alpha (α) is positive, it indicates that the portfolio is generating good returns.
Alpha (α) = Expected Return – Required return as per CAPM Required return as per CAPM = R_f + p (R_m – R_f)
Since, in this question, Beta (β) is not given; first Beta has to be calculated. The following formula can be used for calculation of Beta (β)
= Co-efficient of correlation between
Standard Deviation of Portfolio Standard Deviation of the market
R_m . R_f = 14.3 – 10.1 = 4.2

Statement of Beta and Jensen Alpha of Portfolio

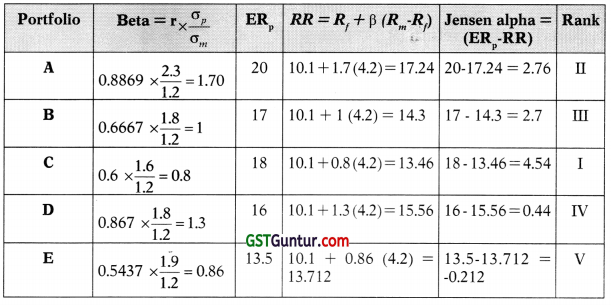
Question 37.
Five portfolios of a mutual fund experienced following result during last 7 years periods:

Portfolio	Average annual return % [Rp]	Standard deviation [Sp]	Correlation with the market return [r]
A	19.0	2.5	0.840
B	15.0	2.0	0.540
C	15.0	0.8	0.975
D	17.5	2.0	0.750
E	17.1	1.8	0.600

Market risk (σ_m) :1.2
Market rate of return (R_m) : 14.0
Risk free rate (R_f) 9.0
Rank the portfolio using
(a) Sharpe’s Method
(b) Treynor’s Method
(c) Jensen’s Alpha [Practice Question]
Answer:
Let portfolio standard deviation be = σ_p
Market standard deviation = σ_m
Coefficient of correlation = r
Portfolio beta (β_p) = \(\frac{\sigma_p r}{\sigma_m}\)
Required portfolio return (R_p) = R_f + β_p (R_m – R_f)
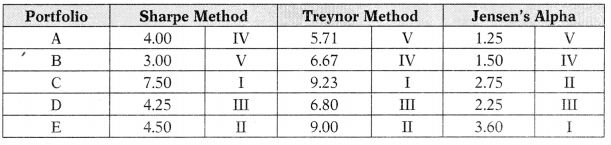
(a) & (b)

(c) Jensen’s Alpha

Portfolio	Beta	Return as per CAPM (Rp)	Rp – (CAPM)
A	1.75	9.0 + 1.75(14.0 – 9.0) = 17.75	1.25
B	0.90	9.0 + 0.90 (14.0 – 9.0 ) = 13.50	1.5
C	0.65	9.0 + 0.65 (14.0 – 9.0) = 12.25	2.75
D	1.25	9.0 + 1.25(14.0 – 9.0) = 15.25	2.25
E	0.90	9.0 + 0.90(14.0 – 9.0) = 13.50	3.6

Required portfolio return (R ) = R_f + P_p(R_m – R_f)

Question 38.
There are two Mutual Funds viz. D Mutual Fund Limited and K Mutual Fund Limited, each having close ended equity schemes.
NAV as on 31-12-2014 of equity schemes of D Mutual Fund Ltd. is Rs. 70.71 (consisting 99% equity and remaining cash balance) and that of K Mutual Fund Ltd. is Rs. 62.50 (consisting 96% equity and balance in cash).
Following is the other information:

	Equity schemes
	D Mutual Fund Ltd.	K Mutual Fund Ltd.
Sharpe Ratio	2	3.3
Treynor Ratio	15	15
Standard deviation	11.25	5

There is no change in portfolios during the next month and annual average cost is Rs. 3 per unit for the schemes of both the Mutual Funds.
If Share Market goes down by 5% within a month, calculate expected NAV after a month for the schemes of both the Mutual Funds.
For calculation, consider 12 months in a year and ignore number of days for particular month. [May 2015] [8 Marks]
Answer:
The two mutual funds have different proportion invested in equity and balance is held as cash. The equity proportion will fluctuate with fluctuations in share market prices, depending upon the value of Beta (β).
The following steps are to be taken for calculation of final NAV.

Step I Calculation of Beta using Sharpe and Treynor Ratios.

Let us find out the Beta on the basis of value of ER – using Treynor ratio.

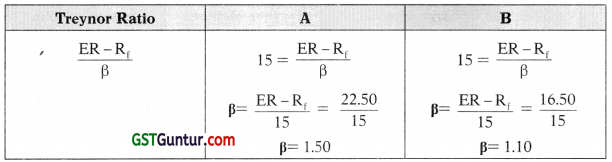
Therefore, the β for the two mutual funds are 1.5 and 1.10 respectively.

Step II Determination of Equity proportion in NRV

	D Mutual Fund Ltd. (Rs.)	K Mutual Fund Ltd. (Rs.)
NAV on 31.12.14	70.71	62.50
% of Equity	99%	96%
Equity element in NAV	70	60
Cash element in NAV	0.71	2.50

Step III Calculation of fall in value of Equity
The beta (β) indicates the sensitivity of equity component of the fund with change in share market. As the market has fallen by 5%, the equity element of both the funds will also fall.
Decrease in Value = (β × % fall in Sec. Market) × NAV (Equity Element)
DMF = (1.5 × 5%) × Rs. 70 = Rs. 5.25
KMF = (1.1 × 5%) × Rs. 60 = Rs. 3.30

Step IV Calculation of balance of Cash after 1 month

	D Mutual Fund Ltd. (Rs.)	K Mutual Fund Ltd. (Rs.)
Annual Expenses	3.00	3.00
Monthly Expenses (Annual Exp./12)	0.25	0.25
Opening Cash	0.71	2.50
Less: Expenses during the month	(0.25)	(0.25)
Cash balance after 1 month	0.46	2.25

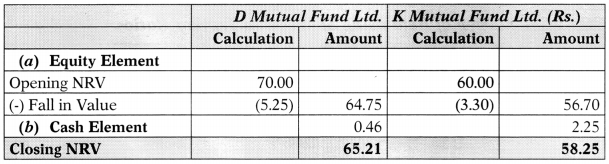
Step V Calculation of NAV after one month

Question 39.
A mutual fund Company introduces two schemes i.e. Dividend plan (Plan D) and Bonus plan (Plan B). The face value of the unit is Rs. 10. On 01-04-2005, Mr. K invested Rs. 2,00,000 each in Plan – D and Plan – B when the NAV was Rs. 38.20 and Rs. 35.60 respectively. Both the plans matured on 31-03-2010. Particulars of dividend and bonus declared over the period are as follows:

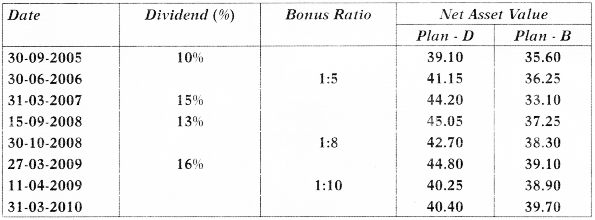
What is the effective yield per annum in respect of the above two plans? [Nov. 2010][8 Marks]
Answer:
Determination of Effective Yield under Dividend Plan (Plan – D)
Units acquired = \(\frac{2,00,000}{38.20}\) = 5235.60

Statement of Units in Hand on 31-3-2010

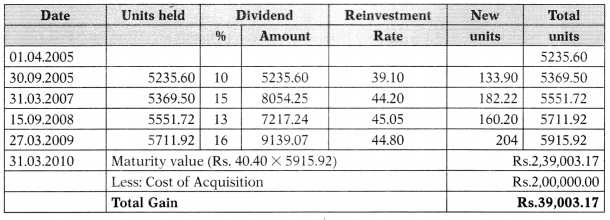
Therefore, Effective Yield under Plan D = \(\frac{R s .39,003.17}{R s .2,00,000} \times \frac{1}{5}\) × 100 = 3.90%

Alternatively, it can be computed by using the IRR method as Follow:
NPV at 4% = -2,00,000 + 1,96,443 = -3,557
NPV at 2% = -2,00,000 + 2,16,473 = 16,473
IRR = LR + \(\frac{N P V \text { at } L R}{N P V \text { at } L R-N P V \text { at } H R}\) (HR – LR) = 2% + \(\frac{16473}{16473-(-3557)}\)(4% – 2%) = 3.645%

Determination of Effective Yield under Bonus Plan (Plan – B)
Statement of Units in Hand on 31-3-2010

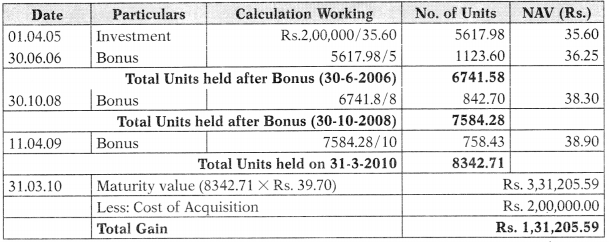
Therefore, Effective Yield under Plan B = ^ 00*066″‘ X I X = 13.12%

Alternatively, it can be computed by using the IRR method as Follow:
NPV at 13% = -2,00,000 + 1,79,765 = -20,235
NPV at 8% = -2,00,000 + 2,25,413 = 25,413
IRP = LP + \(\frac{N P V \text { at } L R}{N P V \text { at } L R-N P V \text { at } H R}\) (HR – LR)
= 8% + \(\frac{25413}{25413-(-20235)}\)(13% – 8%)
= 10.78%

Question 40.
A Mutual Fund Company introduces two schemes – Dividend Plan and Bonus Plan. The face value of the Units is Rs.10 on 1-4-2014. Mr. R invested Rs. 5 Lakh in Dividend plan and Rs.10 lakh in Bonus Plan. The NAV of Dividend Plan is Rs. 46 and NAV of Bonus Plan is Rs. 42. Both the plans matured on 31 -03-2019. The particulars of Dividend and Bonus declared over the period are as follows:

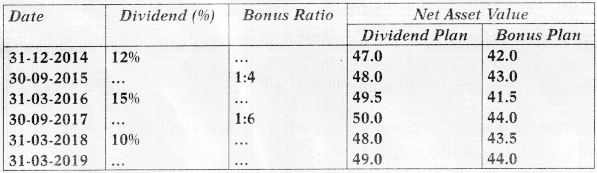
You are required to calculate the effective yield per annum in respect of the above two plans. [May 2019] [8 Marks]
Answer:
Determination of Effective Yield under Dividend Plan
Units acquired = \(\frac{5,00,000}{46}\) = 10,869.57

Statement of Units in Hand on 31-3-2010

Statement showing calculation of gain

31.03.2019	Maturity value (Rs. 49 × 11,724.15)	Rs. 5,74,483.35
	Less: Cost of Acquisition	Rs. 5,00,000.00
	Total Gain	Rs. 74,483.35

Therefore, Effective Yield under Dividend Plan = \(\frac{\text { Rs. } 74,483.35}{\text { Rs. } 5,00,000} \times \frac{1}{5}\) × 100
= 2.98%

Alternatively, it can be computed by using the IRR method as Follow:
NPV at 3% = -5,00,000 + (5,74,483.35 × 0.8626)
= -5,00,000 + 4,95,549.34 = -4,450.66
NPV at 2% = – 5,00,000 + (5,74,483.35 × 0.9057)
= – 5,00,000 + 5,20,309.57
= 20,309.57

IRP = LR + \(\frac{\text { NPV at LR }}{\text { NPV at LR – NPV at HR }}\) (HR – LR)
= 2% + \(\frac{20,309.57}{20,309.57-(-4450.66)}\)(3% – 2%)
= 2.82%

Determination of Effective Yield under Bonus plan
Units acquired = \(\frac{10,00,000}{42}\) = 23.809.52

Statement of Units in Hand on 31-3-2019

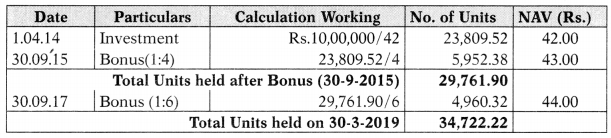
Statement showing Calculation of gain

Therefore, Effective Yield under Bonus Plan = \(\frac{5,27,777.68}{10,00,000} \times \frac{1}{5}\) × 100 = 10.556%

Alternatively, it can be computed by using the IRR method as Follow:
NPV at 11% = -10,00,000 + (15,27,777.68 × 0.59345) = -93,340.34
NPV at 8% = -10,00,000 + (15,27,777.68 × 0.68058) = 39,774.93
IRR = LR + \(\frac{N P V \text { at } L R}{N P V \text { at } L R-N P V \text { at } H R}\)(HR – LR)
= 8% + \(\frac{39,774.93}{39,774.93-(-93,340.34)}\)(11% – 8%) = 8.298% = 8.30%

Question 41.
A mutual fund has two schemes i.e. Dividend plan (Plan A) and Bonus plan (Plan B). The face value of the unit isRs. 10. On 01/04/2016 Mr. Anand invested Rs. 5,00,000 each in Plan – A and Plan – B when the NAV was Rs. 46.00 and Rs. 43.50 respectively. Both the plans matured on 31/03/2019. Particulars of dividend and bonus declared over the period are as follows:

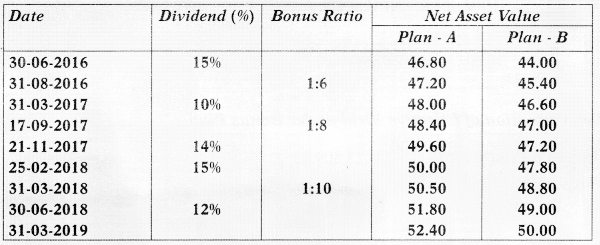
You are required to calculate the effective yield per annum in respect of the above two plans. [May 2019 Old Syllabus] [8 Marks]
Answer:
Determination of Effective Yield under Dividend Plan (Plan A)
Units acquired = \(\frac{5,00,000}{46}\) = 10,869.57
Statement of Units in Hand on 31-3-2019

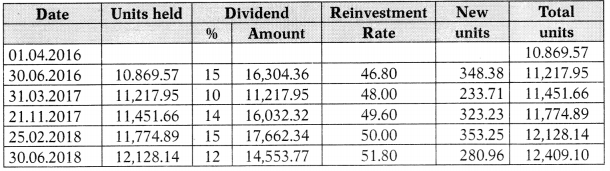
Statement showing Calculation of gain

31.03.2019	Maturity value (Rs. 52.40 × 12,409.10)	Rs. 6,50,236.84
	Less: cost of Acquisition	Rs. 5,00,000.00
	Total Gain	Rs. 1,50,236.84

Calculation of Annual Return
Therefore, Effective Yield under Dividend Plan (Plan A)
\( \frac{R s \cdot 1,50,236.84}{R s \cdot 5,00,000} \times \frac{1}{3}\) × 100 = 10.016%
Alternatively, it can be computed by using the IRR method as Follow:
NPV at 10% = – 5,00,000 + (6,50,236.84 × 0.75131) = – 11,470.56
NPV at 9% = – 5,00,000 + (6,50,236.84 × 0.77218) = 2,099.88
IRR = LR + \(\frac{N P V \text { at } L R}{N P V \text { at } L R-N P V \text { at } H R}\) (HR – LR)
= 9% + \(\frac{2099.88}{2099.88-(-11,470.56)}\)(10% – 9%)
= 9.154%

Determination of Effective Yield under Bonus Plan (Plan B)
Units acquired = \(\frac{5,00,000}{43.50}\) = 11,494.25

Statement of Units in Hand on 31 – 3 – 2019

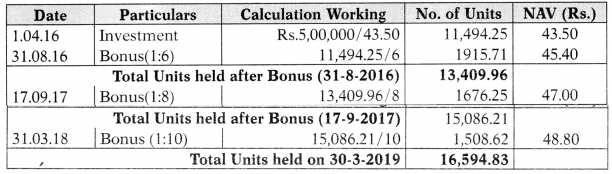
Statement showing Calculation of gain

31.03.19	Maturity value (16,594.83 × Rs. 50)	8,29,741.50
	Less: cost of Acquisition	5,00,000.00
	Total Gain	3,29,741.50

Calculation of Annual Return
Therefore, Effective Yield under Bonus Plan (Plan B)
= \(\frac{3,29,741.50}{5,00,000} \times \frac{1}{3}\) × 100 = 21.98

Alternatively, it can be computed by using the IRR method as follows:
NPV at 20% = -5,00,000 + (8,29,741.50 × 0.57870) = -19,829
NPV at 18% = -5,00,000 + (829,741.50 × 0.60863) = +5,006
IRR = LR + \(\frac{N P V \text { at } L R}{N P V \text { at } L R-N P V \text { at } H R}\)(HR – LR) = 18% + \(\frac{5,006}{5,006+19,829}\) × 2
= 18.403%

Question 42.
T Ltd. has promoted an open-ended equity oriented scheme in 1999 with two plans – Dividend Reinvestment Plan (Plan-A) and a Bonus Plan (Plan-B); the face value of the units was Rs. 10 each. X and Y invested Rs. 5,00,000 each on 1.4.2001 respectively in Plan-A and Plan-B, when the NAV was Rs. 42.18 for Plan A and Rs. 35.02 for Plan-B, X and Y both redeemed their units on 31.3.2008. Particulars of dividend and bonus declared on the units over the period were as follows:

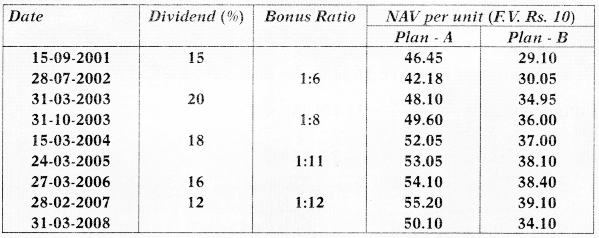
You are required to calculate the annual return for X and Y after taking into consideration the following information:
(i) Securities transaction tax @ 2% on redemption.
(ii) Liability of capital gains to income tax :
(a) Long-term capital gain-exempt; and
(b) Short-term capital gains at 10% plus education cess at 3%. [Nov. 2008 Modified][8 Marks]
Answer:
Determination of Effective Yield under Plan A (Mr. X)
Units acquired = \(\frac{5,00,000}{42.18}\) = 11,853.95

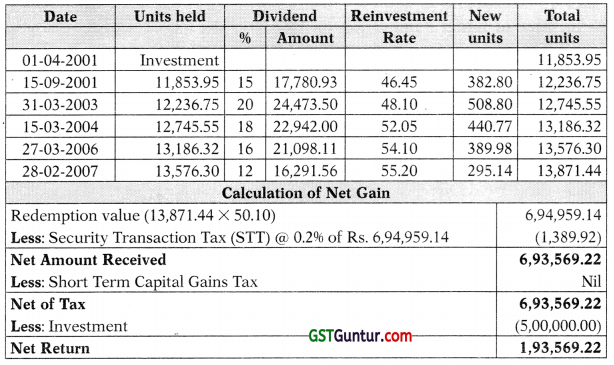
Therefore, Average Annual Return (%) = \(\frac{\mathrm{Rs} .1,93,569.22}{\mathrm{Rs} .5,00,000}\) × 100 = 5.53%

Determination of Return under Bonus Plan (Plan B)

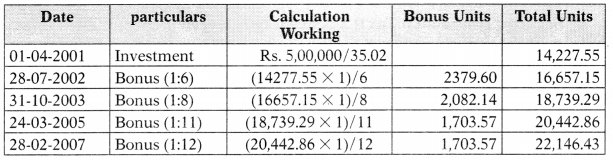
Calculation of Net Gain
Redemption value (22,146.43 × 34.10) Less: Security Transaction Tax (STT) @ 0.2% of Rs. 8,61,750	7,55,193.26 1,510.39
Net Amount Received	7,53,682.87
Less: Investment	(5,00,000.00)
Net Gain	2,53,682.87

Therefore, Average Annual Return (%) = \(\frac{\text { Rs. } 2,53,682.87}{\text { Rs. } 5,00,000} \times \frac{12}{84}\) × 100 = 7.248%

Question 43.
Sun Moon Mutual Fund (Approved Mutual Fund) sponsored open-ended equity oriented scheme “Chanakya Opportunity Fund”. There were three plans viz. ‘A’ – Dividend Reinvestment Plan, ‘B’ – Bonus Plan & ‘C’ – Growth Plan.
At the time of Initial Public Offer on 1.4.1999, Mr. Anand, Mr. Bacchan & Mrs. Charu, three investors invested Rs. 1,00,000 each & chosen ‘B’, ‘C’ & ‘A’ Plan respectively.
The History of the Fund is as follows:

On 31st July, all three investors redeemed all the balance units. Calculate annual rate of return to each of the investors.
Consider:
1. Long-term Capital Gain is exempt from Income tax.
2. Short-term Capital Gain is subject to 10% Income tax.
3. Security Transaction Tax 0.2 per cent only on sale,/redemption of units.
4. Ignore Education Cess. [Nov. 2005][12 Marks]
Answer:
Determination of Effective Yield under Dividend Reinvestment Plan (Mrs. Charu)
Units acquired = \(\frac{1,00,000}{10}\) = 10,000.00

Therefore, Average Annual Return (%) = \(\frac{\text { Rs. } 6,98,969.69}{\text { Rs. } 1,00,000} \times \frac{12}{124}\) × 100 = 67.64%

Determination of Return under Bonus Plan for Mr. Anand

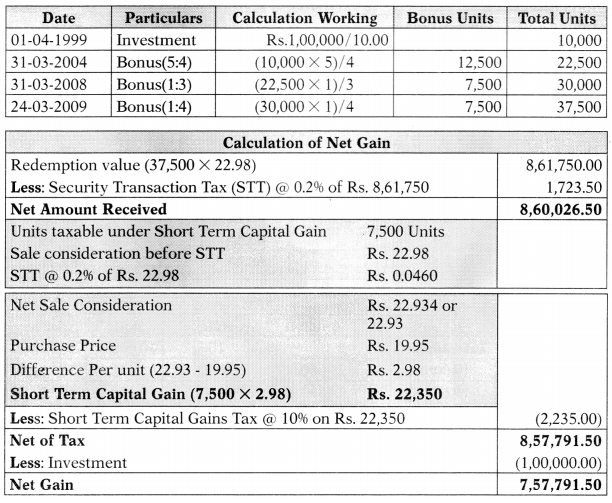
Therefore, Average Annual Return (%) = \(\frac{\text { Rs. } 7,57,791.50}{\text { Rs. } 1,00,000} \times \frac{12}{124}\) × 100 = 73.33%

Determination of Return under Growth Plan for Mr. Bacchan

Particulars	(Amount in Dc)
Redemption value (10,000 × 82.07) Less: Security Transaction Tax (STT) @ 0.2% of Rs. 8,20,700	8,20,700.00 1,641.40
Net Amount Received Less: Short Term Capital Gain Tax @ 10%	8,19,058.60 0.00
Net of Tax Less: Investment	8,19,058.60 (1,00,000)
Net Gain	7,19,058.60

Average Annual Return (%) = \(=\frac{\text { Rs. } 7,19,058}{\text { Rs. } 1,00,000} \times \frac{12}{124}\) × 100 = 69.59%

Question 44.
Cinderella Mutual Fund, an approved mutual fund, sponsored open- ended equity oriented scheme “Rudolf Opportunity Fund”. There are three plans under the scheme viz. ‘A’ – Dividend Re-investment plan, ‘B’ – Bonus plan and ‘C’ – Growth plan.
At the time of initial public offer on 1-4-2009, Mr. Amit, Mr. Ashish and Mr. Arun, three investors invested Rs. 2,00,000 each at face value of Rs. 10 per unit and chosen plan ‘B’, ‘C’ and ‘A’ respectively.
The particulars of the fund over the period are as follows :

On 31st July, 2019 all the three investors redeemed all the balance units. Consider the following :
(a) Long-term capital gain is exempt from Income-tax.
(b) Short-term capital gain is subject to 10% Income-tax.
(c) Security Transaction Tax is 0.2% only on sale/redemption of units,
(d) Ignore Education Cess.
You are required :
(i) To calculate the Effective Yield per annum (annual rate of return) of each of the investors.
(ii) To suggest the name of investor with the highest Effective Yield per annum with the different to his nearest investor.
(Show your calculations up to two decimal points) [Nov. 2019] [10 Marks]
Answer:
Determination of Effective Yield under Dividend Reinvestment Plan (Mr. Arun)
Units acquired = \(\frac{2,00,000}{10}\) = 20,000.00

Therefore, Average Annual Return (%) = \(\frac{\mathrm{Rs} .11,14,906.20}{\text { Rs. } 2,00,000} \times \frac{12}{124}\) × 100 = 53.95%

Determination of Return under Bonus Plan (Mr. Amit)

Calculation of Net Gain

Therefore, Average Annual Return (%) = \(\frac{\text { Rs. } 15,15,583}{\text { Rs. } 2,00,000} \times \frac{12}{124}\) × 100 = 73.33%

Determination of Return under Growth Plan (Mr. Ashish)

Particulars	(Amount in Rs.)
Redemption value (20,000 × 82.07)	16,41,400.00
Less: Security Transaction Tax (STT) @ 0.2% of Rs. 16,41,400	3282.80
Net Amount Received	16,38,117.20
Less: Short Term Capital Gain Tax @ 10%	0.00
Net of Tax	16,38,117.20
Less: Investment	(2,00,000)
Net Gain	14,38,117.20

Average Annual Return (%) = \(\frac{\text { Rs. } 14,38,117}{\text { Rs. } 2,00,000} \times \frac{12}{124}\) × 100 = 69.59%

Question 45.
[Calculation of Fee payable to Manager] ANP Plan, a hedge fund cur-rently has assets of Rs. 20 crore. Mr. X (Chartered Accountant) the manager of fund charges fee of 0.10% of portfolio asset. In addition to it he charges incentive fee of 2%. The incentive will be linked to gross return each year in excess of the portfolio maximum value since the inception of fund. The maximum value the fund achieved so far since inception of fund about one and half year ago was Rs. 21 crores.
You are required to compute the fee payable to CA. X, if return on the fund this year turns out to be
(a) 29%,
(b) 4.5%,
(c) -1.8% [Practice Question]
Answer :
(i) If return is 29%

		Amount (Rs.)
Fixed fee [0.10% of Rs. 20 crore]	(A)	2,00,000
New Fund Value [1.29 × Rs. 20 crore]		25.80 Crore
Excess Value of best achieved (25.8 crore – 21 crore)		4.8 Crore
Incentive Fee (2% of Rs. 4.80 crores)	(B)	9,60,000
Total Fee [(A)+(B)]		11,60,000

(ii) If return is 4.5%

		Amount (Rs.)
Fixed fee [0.10% of Rs. 20 crore]	(A)	2,00,000
New Fund Value [1.045 × Rs. 20 crore]		20.90 Crore
Excess Value of best achieved (20.90 crore – 21 crore)		(Rs. 0.10 crore)
Incentive Fee (as does not exceed best achieved)	(B)	Nil
Total Fee [(A) + B)]		2,00,000

(iii) If return is -1.8%
No incentive only fixed fee of Rs. 2,00,000 will be paid.

Question 46.
On 1st April, an open ended scheme of mutual fund had 300 lakhs units outstanding with Net Assets Value (NAV) of Rs. 18.75. At the end of April, it issued 6 lakh units at opening NAV plus 2% load, adjusted for dividend equa-lization. At the end of May, 3 Lakh units were repurchased at opening NAV less 2% exist load adjusted for dividend equalization. At the end of June, 70% of its available income was distributed.
In respect of April – June quarter, the following additional information are available:

	Rs. in lakh
Portfolio value appreciation	425.47
Income of April	22.950
Income of May	34.425
Income of June	45.450

You are required to calculate
(i) Income available for distribution;
(ii) Issue price at the end of April;
(iii) Repurchase price at the end of May; and
(iv) Net asset value (NAV) as on 30th June. [Nov. 2015] [8 Marks]
Answer:
(i) Calculation of Income available for Distribution

(ii) Calculation of Issue Price at the end of April

Particulars	Rs.
Opening NAV Add: Entry Load 2% of Rs. 18.750	18.750 0.375
Add: Dividend Equalization paid on Issue Price	19.125 0.0765
	19.2015

(iii) Calculation of Repurchase Price at the end of May

Particulars	Rs.
Opening NAV Less: Exit Load 2% of Rs. 18.750Add: Dividend Equalization paid on Issue Price	18.750 (0.375)
	18.375 0.1890
	18.564

(iv) Closing NAV as on 30th June