Dividend Decisions – CA Inter FM Question Bank

Dividend Decisions – CA Inter FM Question Bank is designed strictly as per the latest syllabus and exam pattern.

Dividend Decisions – CA Inter FM Question Bank

Question 1.
What are the determinants of Dividend Policy?
Answer:
Determinants of Dividend Policy: Many factors determine the dividend policy of a company. The factors determining the dividend policy are as follows:
(i) Dividend Payout Ratio
A certain share of earnings to be distributed as dividends has to be worked out. This involves the decision to payout or to retain. The payment of dividends results in the reduction of cash and therefore depletion of assets. In order to maintain the desired level of assets as well as to enhance the investment opportunities, the company has to decide upon the payout ratio.

(ii) Stability of Dividend
Generally investors favour a stable dividend policy. The policy should be consistent and there should be a certain minimum dividend that should be paid regularly.

(iii) Legal, Contractual and Internal Constraints and Restrictions
Legal and contractual requirements have to be followed. All requirements of the Companies Act, SEBI Guidelines, Capital impairment Guidelines, net profit, and insolvency, etc. have to be kept in mind while declaring dividends. in addition, there may be certain internal constraints which are unique to the firm concerned. There may be growth prospects, financial requirements, availability of funds, earning stability and control etc.

(iv) Capital Market Conditions and inflation
Capital market conditions and rate of inflation also play a dominant role in determining the Dividend payout. Good companies will try to compensate for rate of inflation by paying higher dividends. Replacement decisions of the companies also affect the dividend policy.

(v) Owner’s Consideration
This includes the tax status of shareholders, their opportunities for investments, dilution of ownership etc.

Question 2.
What is meant by Stable Dividend Policy why should it be followed?
Answer:
Stable Dividend Policy means regular payment of dividends annually even if the amount of dividends may fluctuate year to year.
A stable Dividend Policy is followed due to the following reasons:

1. It leads to regular cash flow to shareholders
2. This increases the goodwill of the company thereby commanding a higher market price for its shares
3. Government laws covering pension plans encourage the purchase of stocks with high stable dividends.

Question 3.
M Ltd. belongs to a risk class for which the capitalization rate is 10%. It has 25,000 outstanding shares and the current market price is f100. It expects a net profit of ₹ 2,50,000 for the year and the Board is considering dividend of ₹ 5 per share.

M Ltd. is required to raise ₹ 5,00,000 for an approved investment expenditure. Show, how does the MM approach affects the value of M Ltd., if dividends are paid or not paid. (May 2008, 8 marks)
Answer:
A. When dividend is paid
(a) Price per share at the end of year 1
100 = \(\frac{1}{1.10}\left(₹ 5+P_1\right)\)
110 = ₹ 5 +P₁

(b) Amount required to be from issue of new shares
₹ 5,00,000 – (2,50,000 – 1,25,000)
₹ 5,00,000 – 1,25,000 = ₹ 3,75,000

(c) Number of additional shares to be issued
\(\frac{3,75,000}{105}=\frac{75,000}{21}\) shares or say 3572 shares

(d) Value of M Ltd.
(Number of shares × Expected Price per share)
i.e. (25000 + 3,572) × ₹ 105 = 30,00,060

B. When dividend Is not paid
(a) Price per share at the end of year 1
100= \(\frac{\mathrm{P}_1}{1.10} \)
P₁ = 110

(b) Amount required to be raised from issue of new shares
5,00,000 – 2,50,000 = 2,50,000

(c) Number of additional shares to be issued
\(\frac{2,50,000}{110}=\frac{25,000}{11} \) shares or say 2273 shares.

(d) Value of M Ltd.
(25,000 + 2,273) x ₹ 110
= ₹ 30,00,030

Conclusion:
Whether dividend is paid or not, the value remains the same.

Question 3.
RST Ltd. has a capital of ₹ 10,00,000 in equity shares of ₹ 100 each. The shares are currently quoted at par. The company proposes to declare a dividend of ₹ 10 per share at the end of the current financial year. The capitalization rate for the risk class of which the company belongs is 12%. What will be the market price of the share at the end of the year, if
(i) a dividend is not declared?
(ii) a dividend is declared?
(iii) Assuming that the company pays the dividend and has net profits of ₹ 5,00,000 and makes new investments of ₹ 10,00,000 during the period, how many new shares must be issued? Use the MM model. (Nov 2008, 4 marks)
Answer:
As per MM model, the current market price of equity shares is:
P₀ = \(\frac{1}{1+k_e} \times\left(D_1+P_1\right) \)
(i) If the dividend is not declared:
100 = \(\frac{1}{1+0.12} \times\left(0+P_1\right) \)
100 = \(\frac{P_1}{1.12}\)
P₁ = 112
The Market price of the equity share at the end of the year would be 112.

(ii) lithe dividend is declared:
100 = \(\frac{1}{1+0.12} \times\left(10+P_1\right)\)
100 = \(\frac{10+P_1}{1.12}\)
112 = 10+P₁
P₁ = 112 – 10 = ₹102
The market price of the equity share at the end of the year would be ₹ 102.

(iii) In case the firm pays dividend of ₹ 10 per share out of total profits of ₹ 5,00,000 and plans to make new Investment of ₹ 10,00,000, the number of shares to be Issued may be found as follows:

Question 4.
ABC Limited has a capital of ₹ 10 lakhs ¡n equity shares of ₹ 100 each. The shares are currently quoted at par. The company proposes to declare a dividend of ₹ 15 per share at the end of the current financial year. The capitalisation rate for the risk class of which the company belongs is 10%. What will be the market price of share at the end of the year, if
(i) a dividend is declared?
(ii) a dividend is not declared?
(iii) Assuming that the company pays the dividend and has net profits of ₹ 6,00,000 and makes new investments of ₹ 12,00,000 during the period, how many new shares should be issued? Use the MM model. (May 2013, 6 marks)
Answer:
As per MM model, the current market price of equity shares is:
P₀ = \(\frac{1}{1+k_e} \times\left(D_1+P_1\right)\)
(i) If the dividend is declared:
100 = \(\frac{1}{1+0.10} \times\left(15+P_1\right)\)
100= \(\frac{15+P_1}{1.10} \)
110 = 15 + P₁
P₁ = 110 – 15 = ₹ 95
The market price of the equity share at the end of the year would be ₹ 95.

(ii) If the dividend is not declared:
100 = \(\frac{1}{1+0.10} \times\left(0+P_1\right)\)
100 = \(\frac{P_1}{1.10} \)
P₁ = ₹110
The Market price of the equity share at the end of the year would be no.

(iii) If the firm pays dividend of ₹ 15 per share out of total profits of ₹ 6,00,000 and plans to make new investment of ₹ 12,00000, the number of shares to be issued may be found as follows:

Market price of the share ₹ 95
Number of shares to be issued (₹ 7,50,000 / ₹ 95) 7,894.74
or, the firm would issue 7895 shares at the rate of ₹ 95

Question 5.
Buenos Aires Limited has 10 lakh equity shares outstanding at the beginning of the year 2013. The current market price per share is ₹ 150.
The company is contemplating a dividend of ₹ 9 per share, The rate of capitalization, appropriate to its risk class, is 10%.
(i) Based on MM approach, calculate the market price of the share of the company when:
(1) Dividend is declared
(2) Dividend is not declared
(ii) How many new shares are to be issued by the company, under both the above options, if the Company is planning to invest ₹ 500 lakhs assuming a net income of? 200 lakhs by the end of the year? (Nov 2014, 8 marks)
Answer:
As per MM Model:
P₀ = \(\frac{1}{1+\mathrm{K}_e} \times\left(D_1+P_1\right) \)
(i) If the dividend is not declared
150 = \(\frac{1}{1+0.10} \times\left[0+P_1\right] \)
150 = \(\frac{P_1}{1.10} \)
So P₁ = ₹ 165 Market price per share

(ii) If the dividend is declared
150 = \(\frac{1}{1+0.10} \times\left[₹ 9+P_1\right]\)
150 = \(\frac{₹ 9+P_1}{1.10} \)
= 165 – 9 = P₁
P₁ = ₹ 156 Market price per share

In case the firm pays a dividend of ₹ 9 per share out of total profits of ₹ 200 lakhs and plans to make new investment of ₹ 500 lakhs, the number of shares to be issued
or, Net Income (Nl) = 0.20(₹ 1,140 L- ₹ 200 L)
Market Value of Equity = ₹ 1,140 L
Ke = 20%
\(\frac{\text { Net income (NI) for equity – holders }}{\mathrm{Ke}}\) = Market Value of Equity
\(\frac{\text { Net Income (NI) for equity – holders }}{0.20}\) = ₹ 1,140 L
Net income for equity holders = ₹ 228 L
EBIT = 228/0.7
= ₹ 325.71 L

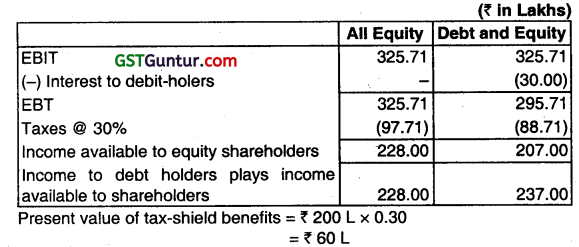
Present value of tax-shield benefits = ₹ 200 L × 030 = ₹ 60L
(i) Value of Restructured Company = ₹ 1,140 L+ ₹ 60 L = ₹ 1,200 L
The impact is that the market value of the company has increased by ₹ 60 lakhs (₹ 1,200 – ₹ 1,140)

(ii) Cost of Capital
Cost of debt (after tax) = 15% (1 – 0.3) = 10.5%

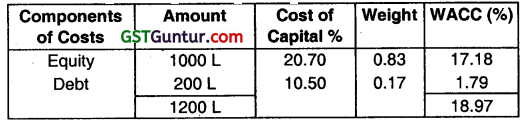
The impact is that the WACC has fallen by 1% (20% – 19%) due to the benefit of tax relief on debt interest payments.

(iii) Cost of Equity (Ke)
Total Value = ₹ 1200 L
Less: Value of debt = (₹ 200 L)
Value of Equity = ₹ 1,000 L
Ke= \(\frac{207 L}{1,000 L} \times 100 \)
Ke=20.70%
The impact is that cost of equity has risen by 0.7% i.e. (20.7% – 20%) due to the presence of financial risk.

Question 6.
The following data relate to two companies belonging to the same risk class:

Required:
(a) Determine the total market value, Equity capitalization rate, and weighted average cost 01 capital for each company assuming no taxes as per M.M. Approach.
(b) Determine the total market value, Equity capitalization rate, and weighted average cost of capital for each company assuming 40% taxes as per M.M. Approach. (Nov 2018, 10 marks)
Answer:
(a)
(i) Calculation of Total Market Value of A Ltd. and B Ltd. as per MM Approach:
V_u = \(\frac{E B I T(1-t)}{K e} \)
Market value of B Ltd. (Unlevered)
V_u = \(\frac{₹ 18,00,000(1-t)}{18 \%}\) = ₹ 1,00,00,000
Market Value of A Ltd. (Levered)
V_g = V_u +TB
= ₹ 1,00,00,000 + ₹ 54,00,000 x Nil
= ₹ 1,00,00,000

(ii) Calculation of Equity Capitalization Rate of A Ltd. end B Ltd.
Ke for A Ltd.
V_g = \(\frac{\text { EBIT – Interest }}{\mathrm{Ke}}\)
46,00,000 = \(\frac{₹ 18,00,000-₹ 6,48,000}{\mathrm{Ke}} \)
Ke = 25.04%
Ke for B Ltd. = 18%

(iii) Calculation of WACC:
B Ltd. = Ke = WACC =18%
A Ltd.

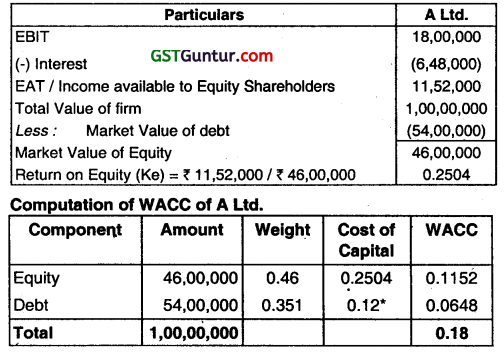
K_d = 12%
WACC= 11.69%

(b)
(i) Calculation of Total Market Value of A Ltd. and B Ltd. as per MM Approach:
Market Value of B Ltd. (Unlevered)
V_u = \(\frac{E B I T(1-t)}{K e}\)
= \(\frac{₹ 18,00,000(1-0.4)}{18 \%}\) = ₹ 60,00,000

Market Value of A Ltd. (Levered)
V_g =V_u +TB
= ₹ 60,00,000 + (₹ 54,00,000 x 40%)
= ₹ 60,00,000 + ₹ 21,60,000
= ₹ 81,60,000

(ii) Calculation of Equity Capitalisation rate of A Ltd. and B Ltd.
K_e for A Ltd.
V_g = \(\frac{\text { EBIT – Interest }}{\mathrm{Ke}}\)
₹ 81,60,000 = \(\frac{₹ 18,00,000-₹ 6,48,000}{\mathrm{Ke}}\)
K_e = 14.12%
K_e for B Ltd. = 18%

(iii) Calculation of WACC:
B Ltd. = Ke = WACC =18%
A Ltd.

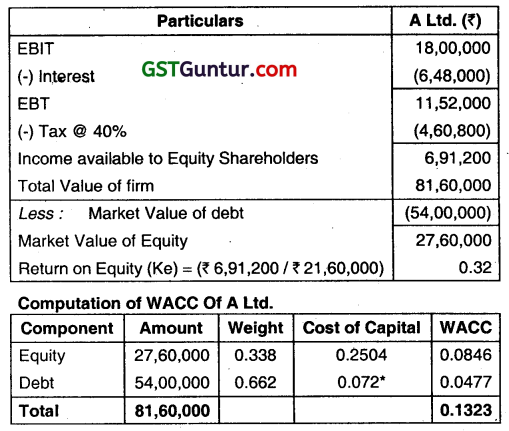
K_d = 12% (1 – 0.4) = 7.2%
WACC = 15.59%

Question 7.
Outline the Dividend Irrelevance Theory of Modigliani and Miller (MM Hypothesis on Dividends)
Answer:
Dividend Irrelevance Theory of Modigliani and Miller: This model explains the irrelevance of the dividend policy. When profits are used to declare dividends, the market price increases. At the same time, there is a fall in the reserves for reinvestment. Hence for expansion, the company raises additional capital by issuing new shares; increase in the overall number of shares will lead to a fall in the market price per share. Hence the shareholders will be indifferent towards the dividend policy.

Modigliani and Miller stated the reason: The value of the firm is determined by its basic earnings power and its risk class, and therefore, the firm’s value depend on its asset investment policy rather than on how earnings are split between dividends and retained earnings.

Question 8.
The following information relates to Maya Ltd.:
Earnings of the company ₹10,00,000
Dividend payout ratio 60%
No. of shares outstanding 2,00,000
Rate of return on investment 15%
Equity capitalization rate 12%
(i) What would be the market value per share as per Walters model?
(ii) What is the optimum dividend payout ratio according to Walter’s model and the market value of company’s share at that payout ratio? (Nov 2010, 8 marks)
Answer:
(i) Computation of market value per share as per Walter’s Model
p = \(\frac{D+(E-D)\left(\gamma / k_e\right)}{k_e}\)
Where, p = Market price per share,
E= Earning per share = ₹ 5
D = Dividend per share = ₹ 3
y = Return earned on investment = 15%

k_e = Cost of equity capital = 12%
p = \(\frac{3+(5-3) \times \frac{0.15}{0.12}}{0.12}=\frac{3+2 \times \frac{.15}{.12}}{0.12} \) = ₹ 45.83

(ii) Optimum Dividend Payout Ratio
As per Walter’s model when the return on investment is more than the cost of equity capital the price per share increases as the dividend payout ratio decreases. Therefore, the optimum dividend payout ratio becomes zero. Therefore, when the payment ratio becomes zero, the market value of the company’s share will be:
= \(\frac{0+(5-0) \times \frac{.15}{.12}}{0.12} \) = ₹ 52.08

Question 9.
X Ltd. earns ₹ 6 per share having a capitalization rate of 10 percent and has a return on investment of 20%. According to Walter’s model, what should be the price of the share at 25% dividend payout? (Nov 2012, 5 marks)
Answer:
Walter’s Model is as follows:
V_e = \(\frac{D+\frac{R_a}{R_b}(E-D)}{R_e} \)
V_e = Market value of the share
R_a = Return on retained earnings
R_e = Capitalisation rate
E = Earnings per share
D = Dividend per share

Therefore, if Walter Model is applied- Market value of the share
V_e = \(\frac{₹ 1.50+\frac{0.20}{0.10}(₹ 6.00-₹ 1.50)}{0.10}\)
or
V_e = \(\frac{₹ 1.50+\frac{0.20}{0.10}(₹ 4.50)}{0.10} \)
or
V_e = \(\frac{₹ 1.50+₹ 9.00}{0.10}=\frac{₹ 10.50}{0.10} \) = ₹ 105

Question 10.
Goldilocks Ltd. was started a year back with equity capital of ₹ 40 lakhs. The other details are as under:
Earnings of the company ₹ 4,00,000
Price Earnings ratio 12.5
Dividend paid ₹ 3,20,000
Number of Shares 40,000
Find the current market price of the share. Use Walter’s Model. Find whether the company’s D/P ratio is optimal, use Walter’s formula. (Nov 2014, 5 marks)
Answer:
Walter’s Model
P₀ = \(\frac{\mathrm{D}}{\mathrm{K}_\theta}+\frac{\frac{\mathrm{r}}{\mathrm{K}_\theta}(E-D)}{\mathrm{K}_\theta} \text { or } \frac{\mathrm{D}+(E-D) \frac{r}{\mathrm{~K}_{\varepsilon}}}{\mathrm{K}_\theta}\)
= \(\frac{₹ 8}{0.08}+\frac{\frac{0.10}{0.08}(1.0-8)}{0.08}\)
= 100 + 31.25
=₹ 131.25

Working Note:
K_e = \(\frac{1}{\text { P/E ratio }} \)
= \(\frac{1}{12.5 \%} \) = 8 %
EPSs = \(\frac{4,00,000}{40,000 \text { shares }}\) = ₹ 10 per share
DPS = \(\frac{3,20,000}{40,000 \text { shares }} \) = ₹ 8 per share
r = \(\frac{4,00,000 \text { (Earnings) }}{40,00,000 \text { (Equity capital) }} \)
= 10%
DIP ratio = \(\frac{₹ 8}{₹ 10}\) x 100 = 80%
As Walter’s Model is in line with the cell or nothing approach and in the present case ‘ r’ ¡s more than ‘k_e’ so it’s a growth firm, so optimal payout ratio for agrowth firm is ‘NIL’.
The company’s DIP ratio is not optimal.
So, at the payout ratio is zero, the market value of the company’s share will be:
= \(\frac{0+(10-0) \frac{0.10}{0.08}}{0.08} \) = ₹ 156.25

Question 11.
You are requested to find out the approximate dividend payment ratio as to have the Share Price at ₹ 56 by using Walter Model, based on following information available for a Company.

	Amount ₹
Net Profit	50 Iakhs
Outstanding 10% Preference Shares	80 Iakhs
Number of Equity Shares	5 Iakhs
Return on Investment	15%
Cost of Capital (after Tax) (ke)	12%

(May 2017, 5 marks)
Answer:
Calculation of Dividend Payout ratio
= \(\frac{\text { Dividend Paid Per Share }}{\text { Earning Per Share }} \times 100 \)
= \(\frac{15.12}{8.4} \times 100\)
= 180%

(1) Calculation of Earning Per Share
= \(\frac{\text { Net Profit }- \text { Preferençe dividend }}{\text { No. of Eq Shares }}\)
= \(\frac{50,00,000-8,00,000}{5,00,000}\)
= 8.4

(2) Calculation of Dividend Per Share
P₀ = \(\frac{D+\frac{r}{k_\theta}(E-D)}{k_e} \)
56 = \(\frac{D+\frac{0.15}{0.12}(8.4-D)}{0.12} \)
56 × 0.12 = D + 10.5 – 1.25 D
6.72 – 10.5 = -0.25 D
D = \(\frac{-3.78}{-0.25}\)
D = 15.12

Question 12.
Following information relating to Jee Ltd. are given:
Particulars
Profit after tax ₹ 10,00,000
Dividend payout ratio 50%
Number of Equity Shares 50,000
Cost of Equity 10%
Rate of Return on Investment 12%
(i) What would be the market value per share as per Wafter’s Model?
(ii) What is the optimum dividend payout ratio according to Walter’s Model and Market value of equity share at that payout ratio? (Nov 2018, 5 marks)
Answer:
(i) Waiter’s model is given by
P = \(\frac{\mathrm{D}+(\mathrm{E}-\mathrm{D}) \times \mathrm{r} / \mathrm{ke}}{\mathrm{Ke}} \)
Where,
P = Market Price per share
E = Earnings Per Share = 20
D = Dividend Per Share = 10
r = Return earned on investment = 12%
ke = Cost of equity capital = 10%
P = \(\frac{₹ 10+(₹ 20-₹ 10) \times \frac{12}{10}}{10}\)
P = ₹ 220

(ii) According to Walter’s Model where the return on investment is more than the cost of equity capital, the price per share increases as the dividend payout ratio decreases. Hence, the optimum dividend payout ratio in this case is nil. So at a pay-out ratio of zero, the market value of the Company’s Share will be:
\(\frac{0+(20-0) \times \frac{12}{10}}{10} \) = ₹ 240

Question 13.
Following figures and information were extracted from the company A Ltd.
Earnings of the company ₹ 10,00,000
Dividend paid ₹ 6,00,000
No. of shares outstanding 2,00,000
Price earning Ratio 10
Rate of return on investment 20%
You are required to calculate:
(i) Current Market price of the share
(ii) Capitalisation rate of its risk class.
(iii) What should be the optimum payout ratio?
(iv) What should be the market price per share at optimal payout ratio? (use Walter’s Model) (Nov 2019, 5 marks)
Answer:
(i) Current Market Price of the share:
EPS = \(\frac{\text { Earnings of the company }}{\text { No. of shares outstanding }} \)
= \(\frac{₹ 10,00,000}{2,00,000 \text { Shares }} \)
= ₹ 5
PE ratio = \(\frac{\text { Market Price }}{\text { EPS }}\)
10 = \(\frac{\text { Market Price }}{\text { ₹ } 5} \)
Current Market price = ₹ 50

The value of the share as per Walter’s model may be found as
follows:
Walter’s model is given by:
P = \(\frac{D+\frac{r}{K_e}(E-D)}{K_e}\)
Where,
P = Market price per share.
E = Earnings per share = 5
D = DMdend per share = 3
R = Return earned on investment = 20%
K_e = Cost of equity capital = 10% or 0.10
P = \(\frac{3+\frac{0.20}{0.10}(5-3)}{0.10} \) = ₹ 70

(ii) Capitalisation rate of its risk class:
Capitalization rate = \(\frac{\text { Earnings }}{\text { Market price } \times \text { No. of shares }} \times 100 \)
= \(\frac{₹ 10,00,000}{₹ 50 \times 2,00,000} \times 100 \)
Capitalisation rate = 10%.

(iii) According to Walter’s model when the rate of return on investment (20%) is more than the cost of equity capital i.e. capitalization rate (10%), the price per share increases as the dividend payout ratio decreases. Hence, the optimum dividend payout ratio in this case is nil.

(iv) Market price per share at optimal payout ratio:
Dividend payout ratio is nil.
∴ P = \(\frac{0+\frac{0.20}{0.10}(5.0)}{0.10}\)
= ₹ 100.

Question 14.
The following figures are extracted from the annual report of RJ Ltd.:
Net Profit ₹ 50 Lakhs
Outstanding 13% preference shares ₹ 200 lakhs
No. of Equity Shares 6 Lakhs
Return on Investment 25%
Cost of Capital (K0) 15%
You are required to impute the approximate dividend pay-out ratio by keeping the share price at ₹ 40 by using Walter’s Model. (Nov 2020, 5 marks)

Question 15.
The following information relates to Maya Ltd. which has a Equity Capitalization Ratio of 12%

Earnings of the Company	₹ 10,00,000	No. of Shares	2,00,000
Dividend Payout Ratio	60%	Rate of Return on Investment	15%

(a) What would be the Market Value per Share as per Walter’s Model?
(b) What is the Optimum Dividend Payout Ratio according to Walter’s Model, and the Market Value of Company’s Share at the Payout Ratio?
Answer:
Computation of Factors under Walters’ Model:

1. Value per Share (Walter’s Model)
= \(=\frac{D+(E-D) \frac{r}{K_e}}{K_E}=\frac{₹ 3+(₹ 5-₹ 3) \times \frac{0.15}{0.12}}{0.12}\)
= ₹ 45.83

2. Optimum Payout Ratio: Since the Company’s earning capacity i.e:ROI (of 15%) ¡s greater than Shareholder’s Expectation (of 12%), the Shareholder’s Wealth would be maximized at “Zero” payout, i.e. Nil Dividend.

3. Value Per Share at Optimum Payout= \(\frac{₹ 0+(₹ 5-₹ 0) \times \frac{0.15}{0.12}}{0.12}\) = ₹ 52.08

Question 16.
The following information relates to Navya Ltd:
Earnings of the Company ‘ ₹ 20,00,000
Dividend payout ratio 60%
No. of Shares outstanding 4,00,000
Rate of return on investment 15%
Equity capitalization rate 12%
Required:
(i) Determine what would be the market value per share as per Walter’s model.
(ii) Compute optimum dividend pay-out ratio according to Walter’s model and the market value of company’s share at that payout ratio.
Answer:
(i) Walter’s model is given by –
P = \(\frac{D+(E-D)\left(r / k_e\right)}{K_e}\)
Where, P = Market price per share,
E = Earnings per share = ₹ 20,00,000 ÷ 4,00,000 = ₹ 5

D = Dividend per share = 60% of 5 = ₹ 3
r = Return earned on investment = 15%
K_e = Cost of equity capital = 12%
P = \(\frac{3+(5-3) \times \frac{0.15}{0.12}}{0.12}=\frac{3+2 \times \frac{0.15}{0.12}}{0.12} \) = ₹ 45.83

(ii) According to Walter’s model when the return on investment is more than the cost of equity capital, the price per share increases as the dividend pay-out ratio decreases. Hence, the optimum dividend pay out ratio is this case is Nil. So, at a payout ratio of zero, the market
value of the company’s share will be:
\(\frac{0+(5-0) \times \frac{0.15}{0.12}}{0.12}\) = ₹ 52.08

Question 17.
Sampathi Ltd., an all Equity Company, has a PAT of ₹ 200 Crores and 10,00,000 Shares of ₹ 10 each outstanding as at the end of the financial year. Its Cost of Capital is 12%. CEE Towers can earn 15% on its investment. Ascertain the value of the Company under Walter’s Model, if the payout ratio is – (a) 20%, (b) 40%, (c) 60%, and (d) 80%. Also draw out the inference from the values obtained under different cases.
Answer:
Note: Firm Value under Walter’s Model (P₀) = \(\frac{D+(E-D) \frac{r}{K_e}}{K_e}\)

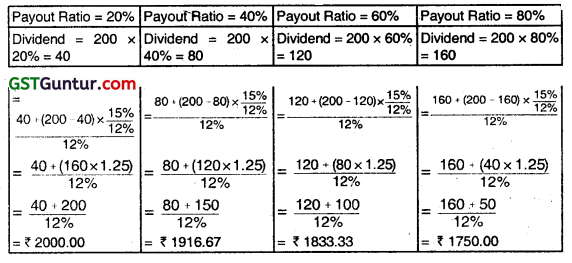
Inference: Since Company’s Returns 15%> Cost of Equity 12%, Investors stand to gain, if they draw tower amount of dividends. As the Dividend Amount increases, the Value of the Firm decreases for a growth firm (r> K_e)

Question 18.
The earnings per share of a company is ₹ 1o and the rate of capitalization applicable to it is lo per cent. The company has three options of paying dividends i.e. (i) 50%, (ii) 75%, and (iii) 100%.
CALCULATE the market price of the share as per Walter’s model if it can earn a return of (a) 15, (b) 10, and (C) 5 percent on its retained earnings. Miscellaneous.
Answer:
Market Price (P) per share as per Walter’s Model is:
P = \(\frac{D+\frac{r}{K_e}(E-D)}{K_e} \)
Where,
P = Price of Share
r = Return on investment or rate of earning
K_e = Rate of Capitalisation or Cost of Equity

Calculation of Market Price (P) under the following dividend payout ratio and earning rates:

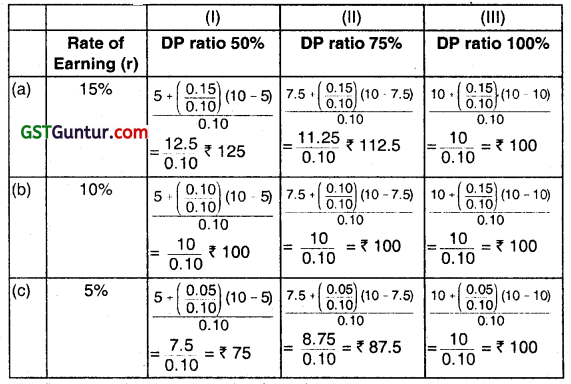
Question 19.
A firm had been paid dividend at ₹ 2 per share last year. The estimated growth of the dividends from the company is estimated to be 5% p.a. Determine the estimated market price of the equity share if the estimated growth rato of dividends (i) rises to 8%, and (ii) falls to 3%. Also find out the present market price of the share, given that the required rate of return of the equity investors is 15.5%. (Nov 2009, 6 marks)
Answer:
In this case the company has paid dividend of ₹ 2 per share during the last year.
The growth rate (g) is 5%. Then, the current year dividend (D₁) with the expected rate of 5% will be ₹ 2.10.
The share price is P_o – \(\frac{D_1}{K_e-g}\)
= \(\frac{₹ 2.10}{0.155-0.05} \)
= ₹ 20

In case the growth rate to 8% then the dividend for the current year. (D₁) would be ₹ 2.16 and market price would be-
= \(\frac{₹ 2.16}{0.155 \cdot 0.08} \)
= ₹ 28.80

In case growth rate tails to 3% then the dividend for the current year (D₁) would be ₹ 2.06 and market price would be
= \(\frac{₹ 2.06}{0.155-0.03} \)
= ₹16.48

Conclusion:
So, the market price of the share is expected to vary in response to change in expected growth rate is dividends.\

Question 20.
In December 2011 AB Co.’s share was sold for ₹ 146 per share. A long-term earnings growth rate of 7.5% is anticipated. AB Co. is expected to pay dividend of ₹ 3.36 per share.
(i) What rate of return an investor can expect to earn assuming that dividends are expected to grow along with earnings at 7.5% per year in perpetuity?
(ii) It is expected that AB Co. will earn about 10% on book Equity and shall retain 60% of earnings. In this case, whether, there would be any change in growth rate and cost of Equity? (May 2012, 6 marks)
Answer:
(i) As per Dividend Discount Model approach the firm’s expected or required return on equity is computed as follows:
K_e = \(\frac{\text { Expected dividend at the end of year } 1\left(D_1\right)}{\text { Current Market Price }\left(P_0\right)} \)
+ Expected Growth Rate of Dividend
Therefore, K_e = + 7.5%
= 0.0230 + 0.075 = 0.098
Or
K_e = 9.80%

(ii) When rate or return of retained earnings (r) is 10% and retention ratio (b) is 60%, new growth rate will be as follows.
g = br i.e.
= 0.10 × 0.60 = 0.06

Thus dividend will also get changed and to calculate this, first, we shall calculate previous retention ratio (b1) and then EPS assuming that rate of return on retained earnings (r) is same. With previous Growth Rate of 7.5% and r = 10% the retention ratio comes out to be:
0.075 = b₁ × 0.10
b₁ = 0.75 and payout ratio = 0.25

With 0.25 payout ratio the EPS will be as follows:
\(\frac{3.36}{0.25} \) = 13.44

With new 0.40(1 -0.60) payout ratio the new dividend will be
D₁ = 13.44 × 0.40 =5.376

Accordingly, new K_e will be
K_e = \(\frac{5.376}{146}\) + 60.%
or, K_e = 9.68%

Question 21.
DEF Ltd. has been regularly paying a dividend of ₹ 19,20,000 per annum for several years and it is expected that same dividend would continue at this level in near future. There are ₹ 12,00,000 equity shares of ₹ 10 each and the share is traded at par.

The company has an opportunity to invest ₹ 8,00,000 in one year’s time as well as further ₹ 8,00,000 in two year’s time in a project as it is estimated that the project will generate cash inflow of ₹ 3,60,000 per annum in three year’s time which will continue forever. This investment is possible it dividend is reduced for next two years. Whether the company should accept the project? Also analyze the effect on the market price of the share, if the company decides to accept the project. (May 2012, 8 marks)
Answer: .
First let us compute cost of Equity (K_e)/PE Ratio
D₁ = \(\frac{19,20,000}{12,00,000}\) = 1.6
P₀ = 10
K_e = \(\frac{D}{P}=\frac{₹ 1.6}{10} \)
P/E = \(\frac{10}{1.6} \) = 6.25

Now we shall compute NPV of the project
NPV = \(\frac{-8,00,000}{(1+0.16)}+\frac{-8,00,000}{(1+0.16)^2}+\frac{3,60,000}{0.16} \times \frac{1}{(1+0.16)^3} \)
= – 6,89,655 – 5,9453O + 14,41,480
= 1,57,295

Conclusion:
As NPV of the project is positive, the value of the firm will increase by ₹ 1,57,295 and spread over the number of shares and the market price per share will increase by 13 paisa.

Question 22.
Following Financial Data for Platinum Ltd. are available:
For the year 2011: (₹ in lakhs)
Equity Shares (₹ 10 each) 100
8% Debentures 125
10% Bonds 50
Reserves and Surplus 200
Total Assets 500
Assets Turnover Ratio 1.1
Effective Tax Rate 30%
Operating Margin 10%
Required rate of return of investors 15%
Dividend payout ratio 20%
Current market price of shares ₹ 13
You are required to:
(i) Draw income statement for the year
(ii) Calculate the sustainable growth rate
(iii) Compute the tair price of the company’s share using dividend discount model, and
(iv) Draw your opinion on investment ¡n the company’s share at current price. (Nov 2012, 8 marks)
Answer:
Working Note:
Asset turnover ratio = 1.1
Total Assets = ₹ 500 lakhs
Turnover 500 lakhs × 1.1 = ₹ 550 lakhs
Interest = ₹ 125 lakhs × 0.08 + ₹ 50 lakhs × 0.10
Operating Margin = 10%
Hence operating cost = (1 – 0.10) ₹ 550 lakhs = ₹ 495 lakh
Dividend Payout = 20%
Tax rate = 30%

(ii) Computation of Sustainable Growth Rate
SGR=G=ROE(1-b)
ROE = \(\frac{\text { PAT }}{\text { NW }}\) and NW = ₹ 1oo lakhs + ₹ 200 lakhs = ₹ 300 lakhs
ROE = \(\frac{₹ 28 \text { lakhs }}{₹ 300 \text { lakhs }} \times 100\) = 9.33%
SGR = 0.0933 (1- 0.20) = 7.47%

(iii) Computation of fair price of share using Dividend Discount Model
P₀ = \(\frac{D_0(1+g)}{K_e-g} \)
Dividends = \(\frac{₹ 5.6 \text { lakhs }}{10 \text { lakhs }} \) = ₹ 0.56
Growth Rate = 7.47%
Hence P₀ = \(\frac{₹ 0.56(1+0.0747)}{0.15-0.0747}=\frac{₹ 0.6018}{0.0753}\) = ₹ 7.99 say ₹ 8.00

(iv) Conclusion:
Since the current market price of share is ₹ 13.00, the share is overvalued. Therefore the investor should not invest in the company.

Question 23.
The following information is collected from the annual reports of J Ltd.:
Profit before tax ₹ 2.50 crore
Tax rate 40 percent
Retention ratio 40 percent
Number of outstanding shares 50,00,000
Equity capitalization rate 12 percent
Rate of return on investment 15 percent
What should be the market price per share according to Gordon’s model of dividend policy? ( May 2015, 4 marks)
Answer:
Profit after tax = ₹ 2.5 crore – 40% = ₹ 1.5 crore
Profit per share
= ₹ 1.5 crore/50,00 0 00 shares
(EPS)=₹ 3

Gordon s formula = P₀ = \(\frac{E(1-b)}{k-b r}\)
P₀ = Present market price
E=EPS
k = Cost of Capit&
b = Retention ratio
r=IRR
br = Growth rate
∴ P₀ = \(\frac{₹ 3(1-0.40)}{0.12-(0.4 \times 0.15)} \)
= \(\frac{1.8}{0.12-0.06}\)
= ₹ 30

Question 24.
The following figures are collected from the annual report of XYZ Ltd.:
Net Profit ₹ 30 lakhs
Outstanding 12% preference shares ₹ 100 lakhs
No. of equity shares 3 lakhs
Return on Investment 20%
Cost of capital Le. (Ke) 16%
CALCULATE price per share using Gordon’s Model when dividend pay-out is (i) 25%; (ii) 50% and (iii) 100%.
Answer:

Price per share according to Gordon’s Model is calculated as follows:
P₀ – \(\frac{E_1(1-b)}{K_e-b r}\)
Here, E₁ =6, K_e=16%

(i) Whei dividend pay-out is 25%
P₀ – \(\frac{6 \times 0.25}{0.16-(0.75 \times 0.2)}=\frac{1.5}{0.16-0.15} \) = 150
(ii) When dividend pay-out is 50%
P₀ = \(\frac{6 \times 0.5}{0.16-(0.5 \times 0.2)}=\frac{3}{0.16-0.10}\) = 50

(iii) When dividend pay-out is 100%
P₀ – \(\frac{6 \times 1}{0.16-(0 \times 0.2)}=\frac{6}{0.16}\) = 37.50

Question 25.
Surabhi Ltd follows Lintner’s Model for dividend distribution. Last year it had declared a dividend of ₹ 5 per share. It has a Target Payout Ratio of 70% of its Earnings. If the EPS for the year is ₹ 10, ascertain the Dividend Payout, it the Surabhi Ltd. views that only 50% of the incremental dividend can be maintained in the years to come? What will be the Dividend Payout if Surabhi Ltd. can maintain 70% or 30% of the incremental dividend?
Answer:
Under Lintner’s Model, Dividend for Year 1 (D₁) = D₀ + af × [(E₁ × tp) — D₀]
Where D₁ = Dividend for Year 1 = To be ascertained
D₀ = Dividend for Year 0 = ₹ 5
af = Adjustment Factor = 30%/50%/ 70%
E₁ = Earnings for Year 1 = ₹ 10
tp = Target Payout Ratio = 70%

Question 26.
The following information is given for QB Ltd.
Earning per share ₹ 12
Dividend per share ₹ 3
Cost of capital 18%
Internal Rate of Return on investment 22%
Retention Ratio 40%
Calculate the market price per share using
(i) Gordons formula
(ii) Walters formula (May 2011, 8 marks)
Answer:
(i) Gordons Formula
Where:
P₀ = \(\frac{E(1-b)}{K-b r} \)
P₀= Present value of Market price per share
E = Earnings per share
K = Cost of Capital
b = Retention Ratio (%)
r =IRR
br = Growth Rate
P₀ = \(\frac{₹ 12(1-0.40)}{0.18-(0.40 \times 0.22)}\)
= \(\frac{₹ 7.20}{0.18-0.088}=\frac{₹ 7.20}{0.092} \) = ₹ 78.26
(ii) Walter Formula
V_c = \(\frac{D+\frac{R_a}{R_c}(E-D)}{R_c} \)

Where:
R_c = Market Price
D = Dividend per share
R_a = IRR
R_c = Cost of Capital
E = Earnings per share
= \(\frac{₹ 3+\frac{0.22}{0.18}(₹ 12-₹ 3)}{0.18} \)
= \(\frac{₹ 3+₹ 11}{0.18} \) = ₹ 77.77

Alternative Answer

As per the data provided in the question the retention ratio comes out to be 75% (as computed below) though mentioned in the question as 40%
(i) Gordons Formula
Retention Ratio = \(\frac{\text { EPS – Dividend Per Share }}{\text { EPS }}=\frac{₹ 12-₹ 3}{₹ 12} \) = 0.75 i.e. 75%
With the retention ratio of 75% market price per share using the Gordons Formula shall be as follows:
P₀ = \(\frac{E(1-b)}{K-b r}\)
P₀ = Present value of market price per share
E = Earnings per share
K = Cost of Capital
b = Retention Ratio (%)
r =IRR
br = Growth Rate
P₀ = \(\frac{12(1-0.75)}{0.18-(0.75 \times 0.22)}=\frac{3}{0.18-0.165}\) = ₹ 200

(ii) Walter Formula V_c = \(\frac{D+\frac{R_a}{K_e}(E-D)}{K_e}\)
V_c = Market price
D = Dividend per share
R_a =IRR
K_e= Cost of Capital
E = Earnings per share
= \(\frac{₹ 3+\frac{0.22}{0.18}(₹ 12-₹ 3)}{0.18}=\frac{₹ 3+₹ 11}{0.18}\) = ₹ 77.77

Question 27.
The following information is supplied to you:
Total Earning ₹ 40 Lakhs
No. of quality Shares (of ₹ 1oo each) ₹ 400000
Dividend Per Share ₹ 4
Cost of Capital 16%
Internal rate of return on investment 20%
Retention ratio 60%
Calculate the market price of a share of a company by using:
(i) Walter’s Formula
(ii) Gordon’s Formula (May 2019, 5 marks)
Answer:
(i) Walter’s Formula:
P = \(\frac{D+(E-D) \times \frac{r}{K e}}{K e}\)
P = \(\frac{₹ 4+\left(\frac{₹ 40,00,000}{₹ 4,00,000}-₹ 4\right) \times \frac{20}{16}}{16}\)
P = ₹ 71.875

Gordon’s formula: –
P₀ = \(\frac{E(1-b)}{K-b \cdot r} \)
Where,
P₀ = Present market price per share
E = Earning per share
b = Retention Ratio (% of earnings retained)
r = Internal rate of return
g =b.r
P₀= \(\frac{E(1-b)}{K-b \cdot r}\)
= \(\frac{₹ 10(1-0.60)}{0.16-(0.6 \times 0.20)} \)
= \(\frac{₹ 4}{0.04} \)
P₀ = ₹ 100

Question 28.
Write short note on the following:
Traditional & Walter Approach to Dividend Policy. (May 2014, 4 marks)
Answer:
Traditional and Walter Approach to Dividend Policy
Traditional approach:
The Graham and Dodd model business its arguments on the following assumptions:
1. Investors are rational
2. Under conditions of uncertainty they turn risk arises.

Postulation
According to Graham & Dodd, investors assign more weight on dividends than on retained earnings. Investors discount distant dividends at a higher rate than they discount nearby dividends. This is because nearby dividends are more certain than distant dividends.

Implication
Under this model the weight attached to dividends is equal to four times the weight attached to retained earnings.

Criticism
The weights provided by Graham and Dodd are based on their subjective judgment and not derived from any empirical analysis.

Walter approach:
1. The Walter’s Model propounded in 1963 by Jones Walter champions the cause of relevance and business its arguments on the following assumption

• The firm is an all-equity firm.
• The firm will use only retained earnings to finance its investments.
• The rate of return on investment is constant and so is the cost of equity. This means that with every additional investment, business risk remains unaltered.
• All earnings are either distributed or retained internally.
• The firm has an infinite life.
• Earnings and dividends don’t change over the life of the firm.

Postulation

• Walter argued that the market price of a share is the sum of the present value of the following two cash flow streams:
• Infinite stream of constant future dividends.
• Infinite stream of capital gains.

Implication

• The optimal payout ratio for a growth firm is nil.
• The payout ratio for a normal firm is irrelevant.
• The optimal payout ratio for a declining firm ¡s 100%.

Criticism

• No external financing.
• Constant rate of return.
• Constant Opportunity Cost.

Question 29.
The following information is taken from ABC Ltd.
Net Profit for the year ₹ 30,00000
12% Preference share capital ₹ 1,00,00,000
Equity share capital (Share of ₹ 10 each) ₹ 60,00,000
Internal rate of return on investment 22%
Cost of Equity Capital 18%
Retention Ratio 75%
Calculate the market price of the share using:
(1) Gordon’s Model
(2) Walter’s Model (Jan 2021, 5 marks)