Risk Analysis in Capital Budgeting – CA Inter FM Question Bank is designed strictly as per the latest syllabus and exam pattern.
Risk Analysis in Capital Budgeting – CA Inter FM Question Bank
Question 1.
Write two main reasons for considering risk in Capital Budgeting decisions. (Nov 2018, 2 marks)
Answer:
Two main reasons for considering risk In Capital Budgeting decision:
- There is an opportunity cost involved while investing in a project for the level of risk. Adjustment of risk is necessary to help make the decision as to whether the returns out of the project are proportionate with the risks borne and whether it is worth investing in the project over the other investment options available.
- Risk adjustment is required to know the real value of the Cash inflows.
Question 2.
A company is considering two mutually exclusive projects X and Y. Project X costs ₹ 30,000 and Project Y ₹ 36,000. You have been given below the net present value probability distribution for each project:
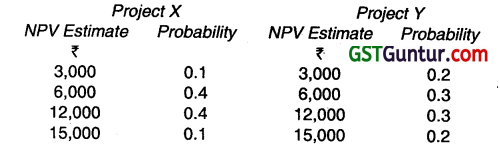
(i) Compute the expected net present value of Projects X and Y.
(ii) Compute the risk attached to each project i.e., Standard Deviation of each probability distribution.
(iii) Which project do you consider more risky and why?
(iv) Compute the probability index of each project. (May 1999, 14 marks)
Answer:
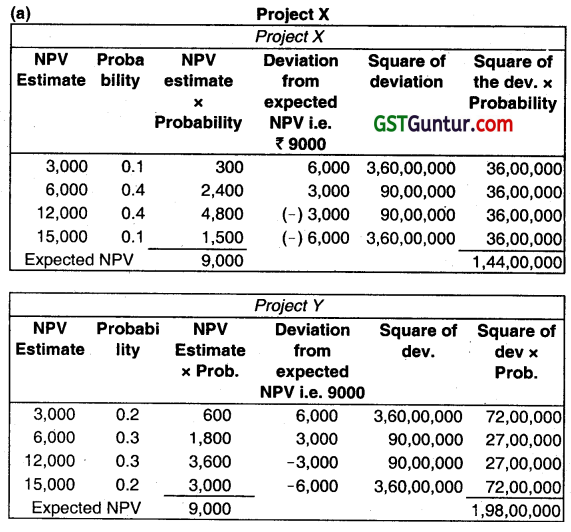
(i) The expected net present value of projects X & Y is ₹ 9,000 each.
(ii) Standard Deviation = \(\sqrt{\text { square of deviation } \times \text { Probability }} \)
In case of Project X-S.D. = \(\sqrt{1,44,00,000} \) = ₹ 3795/-
Project Y-S.D. = \(\sqrt{1,98,00,000} \) = ₹ 4,450/-
Standard deviation
(iii) Coefficient of variation = \(\frac{\text { Standard deviation }}{\text { Expected net P.V. }} \)
Project X = \(\frac{3,795}{9,000}\) = 0.42
Project Y = \(\frac{4,450}{9,000} \) = 0.49 or 0.50
Project Y is riskier since it has a higher coefficient of variation.
(iv) Profitability Index = \(\frac{\text { Discount cash inflow }}{\text { Discount cash outflow }}\)
Project X = \(\frac{9,000+30,000}{30,000}\) = 1.30
Project Y = \(\frac{9,000+36,000}{36,000}\) = 1.25
Question 3.
A Ltd. is considering two mutually exclusive projects X and Y. You have been given below the Net Cash flow probability distribution of each project:
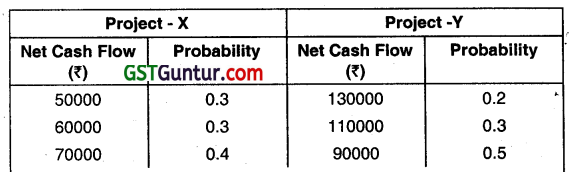
(i) Compute the following:
(a) Expected Net Cash Flow of each project.
(b) Variance of each project.
(c) Standard Deviation of each project.
(d) Coefficient of Variation of each project.
(ii) Identify which project do you recommend. Give reason. (Nov 2020, 10 marks)
Question 4.
What is certainty Equivalent? (May 2018, 4 marks)
Answer:
As per IMA terminology, “An approach to dealing with risk in a capital budgeting context. It involves expressing risky future cash flows in terms of the certain Cash flow which would be considered, by the decision maker, as their equivalént, that is the decision maker would be indifferent between the risky amount and the (lower) riskless amount considered to be its equivalent.”
The Certainty equivalent is a guaranteed return that the management would accept rather than accepting a higher but uncertain return. This approach allows the decision-maker to incorporate his or her utility function into the analysis. In this approach, a set of riskless cash flows is generated in place of the original cash flows.
Question 5.
What is Risk Adjusted Discount Rate? (Nov 2020, 2 marks)
Question 6.
XYZ Ltd. is presently all equity financed. The directors of the company have been evaluating investment in a project which will require ₹ 270 lakhs capital expenditure on new machinery. They expect the capital investment to provide annual cash flows of ₹ 42 lakhs indefinitely which is net of all tax adjustments. The discount rate which it applies to such investment decisions is 14% net.
The directors of the company believe that the current capital structure fails to take advantage of tax benefits of debt, and propose to finance the new project with undated perpetual debt secured on the company’s assets. The company intends to issue sufficient debt to cover the cost of capital expenditure and the after-tax cost of issue.
The current annual gross rate of interest required by the market on corporate undated debt of similar risk is 10%. The after-tax costs of issue are expected to be ₹ 10 lakhs. The company’s tax rate is 30%.
You are required to calculate:
(i) The adjusted present value of the investment
(ii) The adjusted discount rate and
(iii) Explain the circumstances under which this adjusted discount rate may be used to evaluate future investments. (May 2018, 8 marks)
Answer:
Step 1: Unleavened value of the project
PV CFAT discounted with unleavened Re – initial Investment Present
Value of Perpetuity – Initial Investment
= ₹ 42 L/14°70- ₹ 270L
= ₹ 300 L- ₹ 270L
= ₹ 30 L
Step 2: PV of tax benefit on interest
Tax benefit/Interest rate
= 280 × 10% × 30% / 10%
= 8.4/30%
= ₹ 84L
Note: Amount of debt = amount required for project + amount required
for floatation cost = ₹ 270 + ₹ 10 = 280 L
Step 3: After-tax issue expense = ₹ 10 L
(i) Adjusted present value of investment:
Adjusted Present Value =Unleavened value of the project + value of financing effects
Here, Value financing effects =Tax benefit on interest (-) after tax floatation cost
APV=’₹ 30L + (84-10) = ₹ 30L + ₹ 74L
= ₹ 104 L
(ii) Calculation of Adjusted Discount Rate (ADR)
Annual Income / Savings required to allow an NPV to zero Let the Annual Income be x.
(-) ₹ 280 lakhs × (Annual Income / 0.14) = (-) ₹ 104 lakhs
Annual Income / 0.14 = (-) ₹ 104 + ₹ 280 lakhs
Therefore, Annual Income = ₹ 176 × 0.14 = ₹ 24.64 lakhs
Adjusted Discount Rate = (₹ 24.64 lakhs / ₹ 280 lakhs) x 100 = 8.8%
(iii) Useable circumstances
This ADR may be used to evaluate future investments only if the business risk of the new venture is identical to the one being evaluated here and the project is to be financed by the same method on the same terms. The effect on the company’s cost of capital of introducing debt into the capital structure cannot be ignored.
Question 7.
A project requires an initial outlay of ₹ 3,00,000.
The company uses a certainty equivalent method approach to evaluate the project. The risk-free rate is 7%. Following information is available:
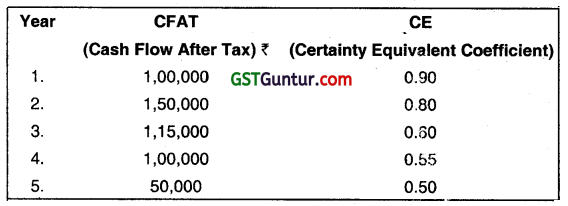
Evaluate the above. Is investment in the project beneficial? (Jan 2021, 5 marks)
Question 8.
Gaurav Ltd. using a certainty-equivalent approach in the evaluation of risky proposals. The following information regarding a new project is as follows:
| Year | Expected Cash Flow | Certainty-equivalent quotient |
| 0 | (4,00,000) | 1.0 |
| 1 | 3,20,000 | 0.8 |
| 2 | 2,80,000 | 0.7 |
| 3 | 2,60,000 | 0.6 |
| 4 | 2,40,000 | 0.4 |
| 5 | 1,60,000 | 0.3 |
Riskless rate of interest on the government securities is 6 percent. DETERMINE whether the project should be accepted?
Answer:
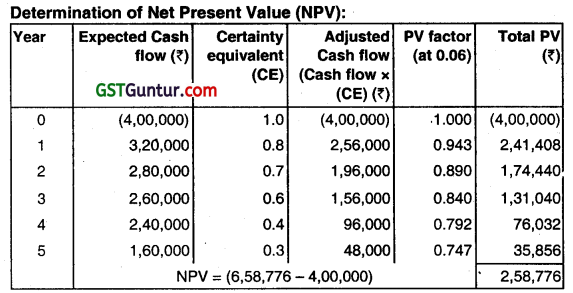
As the Ne Present Value (NPV) is positive the project should be accepted.
Question 9.
An enterprise is investing ₹ 1oo lakhs in a project. The risk-free rate of return is 7%. Risk premium expected by the Management is 7%. The life of the project is 5 years. Following are the cash flows that are estimated over the life of the project.
| Year | Cash flows (₹ ln lakhs) |
| 1 | 25 |
| 2 | 60 |
| 3 | 75 |
| 4 | 80 |
| 5 | 65 |
CALCULATE Net Present Value of the project based on Risk free rate and also on the basis of Risks adjusted discount rate.
Answer:
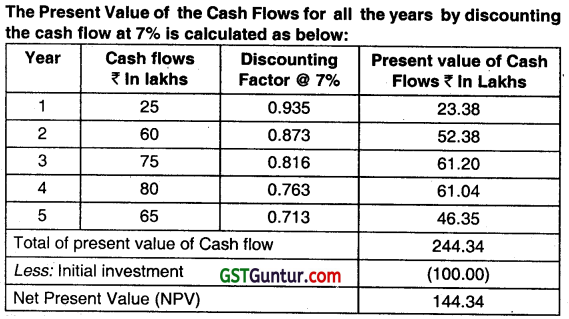
Now when the risk-free rate is 7 % and the risk premium expected by the Management is 7%. So the risk-adjusted discount rate is 7 % +7 % =14%.
Discounting the above cash flows using the Risk-Adjusted Discount Rate would be as below:
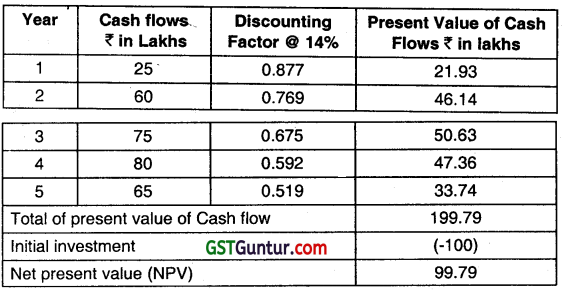
Question 10.
What is sensitivity analysis in Capital budgeting? (May 2009, 6 marks)
Answer:
Sensitivity analysis in Capital Budgeting.
Meaning
Sensitivity analysis is a tool in the hand of firms to analyse change in the project’s NPV or IRR for a given change in one of the variables. It thus shows the measure of sensitivity of a decision due to changes in the values of one or more parameters.
Features
- Sensitivity analysis shows how sensitive a project’s NPV or IRR is to changes in a particular variable.
- It takes care of estimation error by using a number of possible outcomes in evaluating a project.
- It provides different cash flow estimates under the
following assumptions:
- Pessimistic
- Expected
- Optimistic
Concept
Sensitivity analysis starts with a base case scenario i.e. most likely or expected where management determines the estimates of the key primary variables from which it can calculate the base case NPV.
Then, while keeping all other variables equal to their base case values, each variable is changed by a certain percentage below and above its base case value (or, alternatively, is set to its pessimistic and optimistic estimates).
The resulting ‘changed NPV values can then give a picture of the possible variation in or sensitivity of NPV when a given risky variable is mis-estimated.
Steps
- Identify the variables which have an effect on projects NPV or IRR.
- Define the mathematical relationship between the variables.
- Analyse the implication to change in each of the variables on the project’s NPV or IRR.
Advantages
1. Sensitivity Analysis is useful in identifying the crucial variables that could contribute the most to the riskiness of the investment.
2. It indicates how bad a mis-estimating a variable can be before the investment becomes unacceptable.
3. It helps in understanding the project in total.
4. It guides the decision-maker to concentrate only on relevant variables.
Dis advantages
1. The sensitivity analysis does not provide estimate of likelihood for each possible result.
2. Examining the effect of change in each variable in isolation is less meaningful when there are interdependencies among the variables.
3. It may double count the risk if one uses a risk-adjusted discount rate.
4. In addition estimates of a variable may be serially dependent over time so that a forecast error in one year may propagate higher errors in subsequent years, causing a greater impact on NPV.
5. It uses different values of uncertain variables purely on ad-hoc basis. This is unscientific.
6. Its assumption of variable to be completely unrelated is vague and misleading.
Question 11.
From the following details relating to a project, analyse the sensitivity of the project to changes in the Initial Project Cost, Annual Cash Inflow, and Cost of Capital:
| Particulars | |
| Initial Project Cost | ₹ 2,00,00,000 |
| Annual Cash Inflow | ₹ 60,00,000 |
| Project Life | 5 years |
| Cost of Capital | 10% |
To which of the 3 factors, the project is most sensitive lithe variable is adversely affected by 10%?
The cumulative Present Value Factor for 5 years for 10% is 3.791 and for 11% is 3.696. (Nov 2018, 5 marks)
Answer:
Calculation of NPV through Sensitivity Analysis
| Particulars | ₹ |
| PV of Cash inflows (₹ 60,00,000 × 3.791) (-) initial Project Cost | 2,27,46,000 (2,00,00,000) |
| NPV | 27,46,000 |
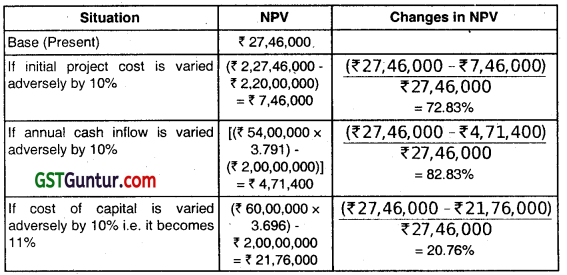
Conclusion: Project is most sensitive to ‘annual cash in flow’.
Question 12.
Explain the steps of Sensitivity Analysis. (May 2019, 4 marks)
Answer:
Steps of Sensitivity Analysis:
Sensitivity Analysis is conducted by following the steps as below:
1. Finding variables
Which have an influence on the NPV (or IRR) of the project.
2. Establishing Mathematical Relationship
Between the variables.
3. Analysing
The effect of the change in each of the variables on the NPV (or IRR) of the project.
Question 12.
XY Ltd. has under Its consideration a project with an initial investment of ₹ 1,00,000. Three probable cash inflow scenarios with their probabilities of occurrence have been estimated as below:
| Annual cash inflow (₹) | 20,000 | 30,000 | 40,000 |
| Probability | 0.1 | 0.7 | 0.2 |
The project life Is 5 years and the desired rate of return is 20%. The estimated terminal values for the project assets under the three probability alternatives, respectively are zero, ₹ 20,000 and₹ 30,000.
You are required to:
(i) Find the probable NPV;
(ii) Find the worst-case NPV and the best-case NPV; and
(iii) State the probability occurrence of the worst case, if the cash flows are perfectly positively correlated over time. (May 2010, 12 marks)
Answer:
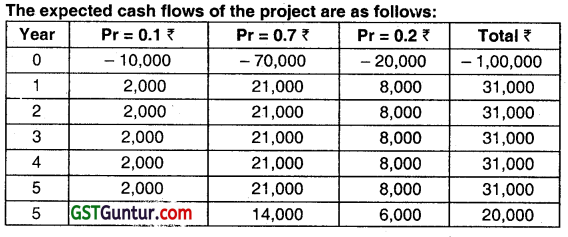
(i) NPV based on expected cash flows would be as follows:
= \(₹ 1,00,000+\frac{₹ 31,000}{(1+0.20)^1}+\frac{₹ 31,000}{(1+0.20)^2}+\frac{₹ 31,000}{(1+0.20)^3}+\frac{₹ 31,000}{(1+0.20)^4}+\frac{₹ 31,000}{(1+0.20)^5}+\frac{₹ 20,000}{(1+0.20)^5}\)
= -₹ 1,00,000 + ₹ 25,833.33 + ₹ 21,527.78 + ₹ 17,939.81 + ₹ 14,949.85 + ₹ 12,458.20 + ₹ 8,037.55 = 746.52
(ii) For the worst case, the flows from the cash flow column farthest on the left are used to calculate NAV.
= \(-₹ 10,000+\frac{₹ 2,000}{(1+0.20)^1}+\frac{₹ 2,000}{(1+0.20)^2}+\frac{₹ 2,000}{(1+0.20)^3}+\frac{₹ 2,000}{(1+0.20)^4}+\frac{₹ 2,000}{(1+0.20)^5}\)
= – ₹ 10,000 + ₹ 1,666.67+ ₹ 1,388.89+ ₹ 1.157.41 + ₹ 964.51 + ₹ 803.76
N.P.V = ₹ – 4,018.76
For the best case, the cash flows from the cash flow column farthest on the right are used to calculated NPV
= \(₹ 20,000, \frac{₹ 8,000}{(1+0.20)^1}, \frac{₹ 8,000}{(1+0.20)^2} \cdot \frac{₹ 8,000}{(1+0.20)^3}, \frac{₹ 8,000}{(1+0.20)^4}, \frac{₹ 8,000}{(1+0.20)^5}, \frac{₹ 8,000}{(1+0.20)^5}\)
= – ₹ 20,000 + ₹ 6,666.67 + ₹ 5,555.56 + ₹ 4,629.63 + ₹ 3,858.02 + ₹ 3,215.02 + ₹ 2,411.26
N.P.V = ₹ 6,336.16
(iii) If the cash flows are perfectly dependent, then the low cash flow in the first year will mean a low cash flow ¡n every year. Thus, the possibility of the worst case occurring is the probability of getting ₹ 2,000 net cash flow in year 1 or 20%.
Question 13.
Shivam Ltd. is considering two mutually exclusive A and B. Project A costs ₹36,000 and project B ₹ 30,000. You have been given below the net present value probability distribution for each project.

(i) Compute the expected net present values of projects A and B.
(ii) Compute the risk attached to each project i.e. standard deviation of each probability distribution.
(iii) Compute the profitability index of each project.
(iv) Which project do you recommend? State with reasons. (May 2009, 14 marks)
Answer:
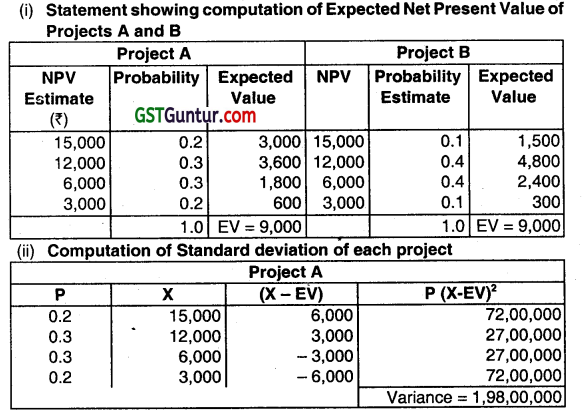
Standard Deviation of Project A = \(\sqrt{1,98,00,000}\) = ₹ 4,450

Standard Deviation of Project B = \(\sqrt{1,44,00,000}\) = ₹ 3,795
(iii) Computation of profitability of each project
Profitability index = Discount cash ¡nf low /Initial outlay
In case of Project A: P1 = \(\frac{9,000+36,000}{36,000}=\frac{45,000}{36,000} \) = 1.25
In case of Project B: P1 = \(\frac{9,000+30,000}{30,000}=\frac{39,000}{30,000} \) = 1.30
(iv) Recommendation: Measurement of risk is made by the possible variation of outcomes around the expected value and the decision will be taken in view of the variation in the expected value where two project have the same expected value, the decision will be the project which has smaller variation in expected value. In the selection of one of the two projects A and B, Project B Is preferable because the possible profit which may occur is subject to less variation (or dispersion). Much higher risk is lying with project A.
Question 14.
Indian Newsprint Ltd. (INL) a leading manufacturer of newsprint in the country, is planning to start manufacturing cardboard unit. Planning & Strategy division of the company has placed before the board of directors the “Detail Project Report” of the card board unit. The report, inter alla, includes the following cash flow:
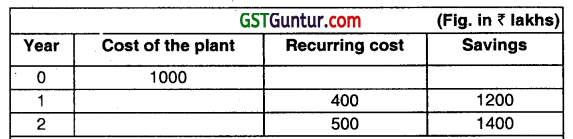
The cost of the capital is 9%. –
You are required to measure the sensitivity of the project to changes ¡n the levels of plant value, recurring cost and savings (considering each factor at a time) such that the NPV becomes zero. The present value factor at 9% are given below:

Advise the board of directors which factor is the most sensitive to affect the acceptability of the project? (Nov 2017, 8 marks)
Answer:

Question 15.
From the following data, Is relating to a project, analyse the sensitivity of the project to changes in initial project cost, annual cash inflow, and cost of capital:
| Initial Project Cost (₹) | 120,000 |
| Annual Cash Inflow (₹) | 45,000 |
| Project Life (Years) | 4 |
| (Cost of Capital) | 10% |
Required:
Examine which of the three factors, the project is most sensitive? (Use annuity factors: for 10% 3.169 and 11% 3.103).
Answer:
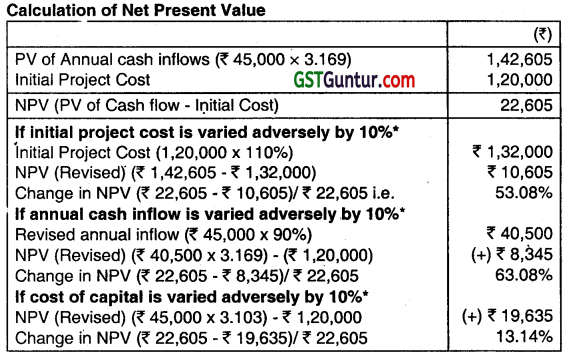
Conclusion: The project is most sensitive to annual cash inflows’
(It is assumed that adverse variation is 10%)
Question 16.
Shiv Limited is thinking of replacing its existing machine by a new machine which would cost ₹ 60 lakhs. The company’s current production is ₹ 80,000 units, and is expected to increase to ₹ 1,00,000 units, if the new machine is bought. The selling price of the product would remain unchanged at ₹ 200 per unit. The following is the cost of producing one unit of product using both the existing and new machine:
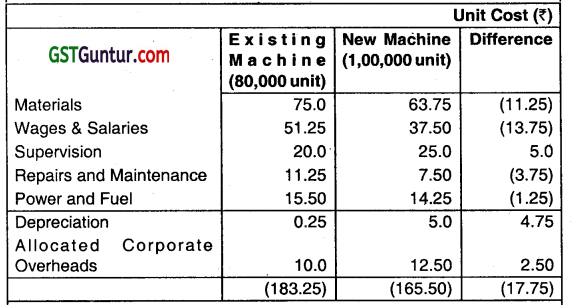
The existing machine has an accounting book value of ₹ 1,00,000, and it has been fully depreciated for tax purpose. It is estimated that machine will be useful for 5 years. The supplier of the new machine has offered to accept the old machine for ₹ 2,50,000. However, the market price of old machine today is ₹ 1,50,000 and it is expected to be ₹ 35,000 after 5 years. The new machine has a life of 5 years and a salvage value of ₹ 2,50,000 at the end of its economic life. Assume corporate Income tax rate at 40%, and depreciation is charged on straight-line basis for Income-tax purposè’s. Further assume that book profit is treated as ordinary income for tax purposes. The opportunity cost of capital of the Company is 15%.
Required:
(i) ESTIMATE net present value of the replacement decision.
(ii) CALCULATE the internal rate of return of the replacement decision.
(iii) Should Company go ahead with the replacement decision?
ANALYSE.
Answer:

Market Value of Old Machine: The old machine could be sold for ₹ 1,50,000 in the market. Since the exchange value is more than the market value, this option is not attractive. This opportunity will be lost whether the old machine is retained or replaced. Thus, on incremental basis, it has no impact.
Depreciation Base:
Old machine has been fully depreciated for tax purpose. Thus, the depreciation base of the new machine will be its original cost i.e. ₹ 60,00,000.
Net Cash Flows:
Unit cost includes depreciation and allocated overheads. Allocated overheads are allocated from corporate office therefore they are irrelevant. The depreciation tax shield may be computed separately. Excluding depreciation and allocated overheads, unit costs can be calculated. The company will obtain additional revenue from additional 20,000 units sold.
Thus, after-tax savings, excluding depreciation, tax shield, would be
= (100,000(200- 148) – 80,000(200 – 173)) × (1 – 0.40)
= (52,00,000 – 21 ,60,000) × 0.60
= ₹ 18,24,000
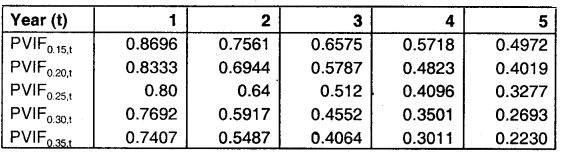
After adjusting depreciation tax shield and salvage value, net cash flows and net present value are estimated.

Alternately Net Cash flows from operation can be calculated as follows:
Profit before depreciation and tax = ₹ 1,00,000 (200 -148) – 80,000 (200 -173)
= ₹ 52,00,000 – 21,60,000
= ₹ 30,40,000
So, profit after depreciation and tax is (30,40,000 -11,50,000) × (1- 0.40) = ₹ 11,34,000
So profit before depreciation and after tax is:
₹ 11,34,000 + ₹ 11,50,000 (Depreciation added back) = ₹ 22,84,000
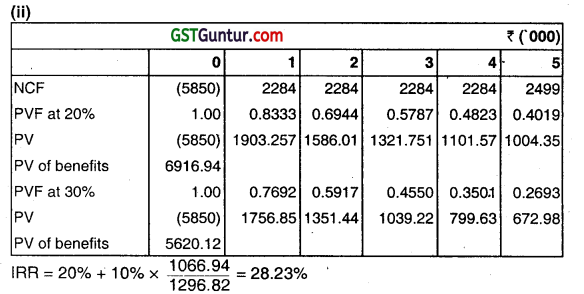
(iii) Advise:
The Company should go ahead with replacement project, since it is positive NPV decision.