Derivatives Analysis And Valuation – CA Final SFM Study Material

Derivatives Analysis And Valuation – CA Final SFM Study Material is designed strictly as per the latest syllabus and exam pattern.

Derivatives Analysis And Valuation – CA Final SFM Study Material

Part-1(Theory)

Question 1.
Write a short note on Embedded Derivatives. [May 2018] [Nov. 2011] [Nov. 2008] [5 Marks]
Answer:
An embedded derivative is a derivative instrument that is embedded in another contract, called the host contract. The host contract might be a debt or equity instrument, a lease, an insurance contract or a sale or purchase contract. They are a result of financial engineering, though some may arise inadvertently due to market practices and contracting arrangements. There is intentional shifting of risks between the parties. They may cause modification to a contract’s cash flow, if there is any change in specified variable.

A derivative requires to be marked to market through the Income statement, f Embedded derivatives are also marked-to-market. This requirement on embedded derivative is designed to ensure that mark-to-market is not avoided by including or embedding a derivative in another contract or financial instrument which is not marked-to-market through the Income statement.

Question 2.
Distinguish between a Future contract and an Option contract. [Nov. 2018] [5 Marks]
Answer:
The following are the points of differences between a Future contract and an option contract.

Basis	Future contract	Option contract
Definition	A future contract is a contract between two parties to exchange assets or services at a specified time in the future at a price agreed upon at the time of the contract. It is exchange traded.	An option is a contractual agree­ment that gives the option buyer the right, but not the obligation, to purchase or to sell a specified instrument at a specified price at any time before maturity or on maturity. It is exchange traded.
Settlement/ Cash Flow	Profit/Loss is settled on a daily basis based on movement in cur­rent Future prices.	Option writer collects premium at the inception of the contract.
Price Fixation	Determined by the market forces.	Exercise price fixed by the stock exchange. Premium is market driven.
Obligation to perform	Both the parties are under obligation to perform.	Only the writer of the option is under obligation to perform. The option buyer has discretion.
Closure of Contract	Physical delivery Payment of price differential Taking an opposite position	Physical delivery Payment of price differential Taking an opposite position.

Question 3.
What is the significance of an underlying in relation to a derivative Instrument? [May 2011] [4 Marks]
Answer:
The derivative instruments are the outcome of financial engineering and their value is based on some underlying asset. The underlying may be a share, a commodity or any other asset which has a marketable value which is subject to market risks. The importance of underlying in derivative instruments is as follows:

• All derivative instruments are dependent on an underlying to have value.
• The change in value in a forward contract is broadly equal to the change in value in the underlying.
• In the absence of a valuable underlying asset the derivative instrument will have no value.
• On maturity, the position of profit/loss is determined by the price of underlying instruments. If the price of the underlying is higher than the contract price the buyer makes a profit. If the price is lower, the buyer suffers a loss.

Question 4.
State the various assumptions of Black Scholes Model [May 2015] [4 Marks]
Answer:
The following are the assumptions of Black Scholes Model;

• The option is a European option.
• There are no transaction charges.
• There are no taxes.
• The risk free rate is known and is constant over the life of the option.
• Stocks do not pay dividend.
• Stock returns are normally distributed over a period of time.
• The variance of the return is constant over the life of an option.

Question 5.
Write short note on the Factors affecting value of an option [May 2012] [4 Marks]
Answer:
The price of an option is a function of spot price, exercise price, time to expiration, risk free rate of return, volatility and dividends. These are explained as follows:
1. Market Price of the underlying asset: Call option is directly related to the spot price so the value of call option increases with rise in spot prices. The put option has inverse relation with the spot price, so its value decreases with increase in spot price.

2. Exercise price or Strike price (X): Call is inversely related to the strike price and Put is directly related with strike price.

3. Time to Expiration: The price of both Call and Put are directly related to the time. The longer the maturity, the higher will be the price of options.

4. Volatility: The price of both Call and Put are directly related to the volatility. The higher the movement in underlying, the higher will be the price of options.

5. Risk free rate of return: The Call premium is higher with higher rate of interest and vice versa, whereas Put option price is inversely related to the risk free rate of return.

6. Dividends: if the dividends are receivable before the due date of expiration of an option and the market price is cum-dividends then put option will be higher and call option premium will be lower.

Question 6.
Define the following Greeks with respect to options: [Nov. 2015] [4 Marks]
1. Delta
2. Gamma
3. Vega
4. Rho
Answer:
1. Delta: It is the degree to which an option price will move, given a small change in the underlying stock price. A deeply out of money call will have delta very close to zero and a deeply in the money call will have a delta close to 1.

For example, if the delta is 0.1, Re.l change in underlying will change the value of option by Re. 0.10. If delta is 0.95, a Re.l change in underlying will change the value of option by Rs. 0.95.

2. Gamma: It measures how fast the delta changes for a small change in the underlying stock price. It is the delta of the delta. If a portfolio is hedged using delta-hedge technique, the gamma should be small. A small gamma will not bring much change in the delta and therefore portfolio will not require adjustment.

3. Vega: It measures the sensitivity of option value to change in volatility. / Vega indicates an absolute change in option value for a one percentage change in volatility.

4. Rho: It measures the sensitivity of option value to change in interest rate. It is the change in option price given a one percentage point change in the risk-free interest rate. Rho indicates the absolute change in option value for a one percent change in the interest rate.

Part-2 (Numerical Problems: Topic Wise In Chronological Order)

Question 1.
[Probability using continuous compounding] Sumana wanted to buy shares of EIL which has a range of ₹ 411 to ₹ 592 a month later. The present price per share is ₹ 421. Her broker informs her that the price of this share can sore up to ₹ 522 within a month or so, so that she should buy a one month CALL of EIL. In order to be prudent in buying the call, the share price should be more than or at least ₹ 522 the assurance of which could not be given by her broker.
Though she understands the uncertainty of the market, she wants to know the probability of attaining the share price ₹ 592 so that buying of a one month CALL of EIL at the execution price of ₹ 522 is justified. Advise her. Take the risk free interest to be 3.60% and e^0.036 = 1.037. [May 2012] [8 Marks]
Answer:
The Probability of Price going up is given by the following formula. In this formula, the probability is calculated using continuous compounding.
p = \(\frac{e^{r t}-d}{u-d}\)
Where,
p = is the probability of the price going up.
eⁿ = future value using continuous compounding
d = wealth ratio if the price falls.
u = wealth ratio if the price rise.
eⁿ = e^0.036
d = 411/421 = 0.976
u = 592/421 = 1.406
p = \(\frac{e^{0.036}-0.976}{1.406-0.976}=\frac{1.037-0.976}{0.43}\) = \(\frac{0.061}{0.43}\) = 0.1418
Thus, probability of rise in price 0.1418
Although, the Probability of rise in price is low, Sumana should base her decision on the price of option.

Question 2.
Consider a two year American call option with a strike price of ₹ 50 on a stock the current price of which is also ₹ 50. Assume that there are two time periods of one year and in each year the stock price can move up or down by equal percentage of 20%. The risk free interest rate is 6%. Using binominal option model, calculate the probability of price moving up and down. Also draw a two-step binomial tree showing prices and payoffs at each node. [May 2009] [8 Marks]
Answer:
The Probability of Price going up is given by the following formula. In this formula, the probability is calculated without using continuous compounding.
P = \(\frac{R f-d}{u-d}\)
Rf = Future value at risk free rate of interest.
d = 40/50 = 0.8 (The price may go 20% down from the present price of 50 ie. 40)
u = 60/50 = 1.2 (The price may go 20% up from the present price of 50 i.e. 60)
p = \(\frac{1.06-0.8}{1.2-0.8}=\frac{0.26}{0.40}\) = 0.65
Thus, probability of rise in price 0.65

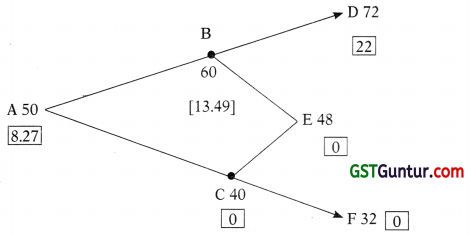
The pay off at Node B is Rs. 10 (60-50) or Rs. 13.49 whichever is higher, therefore it is 13.49 and at Node D it is Rs. 22 (72-50)
The Present value after 1 year of expected pay off after two years is \(\frac{22(0.65)+0(0.35)}{1.06}\) = Rs. 13.49
The expected pay off at Node A should be = \(\frac{13.49(0.65)+0(0.35)}{1.06}\) =Rs. 8.27

Question 3.
Mr. Dayal is interested in purchasing equity shares of ABC Ltd. which are currently selling at ₹ 600 each. He expects that price of share may go up to ₹ 780 or may go down to ₹ 480 in three months. The chances of occurrence of such variations are 60% and 40% respectively. A call option on the shares of ABC Ltd. can be exercised at the end of three months with a strike price of ₹ 630.
(i) What combination of share and option should Mr. Daya! select if he wants a perfect hedge?
(ii) What should be the value of option today (the risk free rate is 10% p.a.)?
(iii) What is the expected rate of return on the option? [Nov. 2015] [5 Marks]
Answer:
(i) The combination of share and option that Mr. Dayal should select depends on the hedge ratio which can be computed as follows:
Hedge Ratio ∆ = \(\frac{C_u-C_d}{S_u-S_d}=\frac{150-0}{780-480}=\frac{150}{300}\) = 0.50
Cu = value of call option if price rises.
Su = value of Share if price rises.
Cd = value of call option if price falls.
Sd = value of share if price falls.
Mr. Dayal should take opposite positions in the share and the call option for a perfect hedge. If he is long on shares, he must sell call option. This means that for purchase of every 0.50 share, he should write 1 call option. As the price of share today is Rs. 600, he should invest Rs. 300 today and receive the call premium.

(ii) Value of Option today:

If price of share comes out to be ₹ 780 then
Value of purchased share will be (0.50 × ₹ 780)	₹ 390
Loss on account of Short Position in call option at an exercise price of Rs. 630 (? 780 – ? 630)	₹ 150
Net position after three months	₹ 240
If price of share comes out to be ₹ 480 then
Value of purchased share will be(0.50 × ₹ 480)	240
Loss on account of Short Position in call option at an exercise price of Rs. 630	Nil
Net position after three months	₹ 240

Therefore, Premium (P) shall be computed as follows:
(₹ 300 – P) 1.025 = ₹ 240
P = ₹ 65.85

(iii) Expected Return on the Option:
Expected Option Value at the time of maturity
= (₹ 780 – ₹ 630) × 0.60 + ₹ 0 × 0.40 = ₹ 90
Expected Rate of Return = \(\frac{90-65.85}{65.85}\) × 100 = 36.67%

Question 4.
AB Ltd.’s equity shares are presently selling at a price of Rs.500 each. An investor is interested in purchasing AB Ltd.’s shares. The investor expects that there is a 70% chance that the price will go up to Rs. 650 or a 30% chance that it will go down to Rs. 450, three months from now’. There is a call option on the shares of the firm that can be exercised only at the end of three months at an exercise price of Rs. 550.
Calculate the following:
(i) If the investor wants a perfect hedge, what combination of the share and option should he select ?
(ii) Explain how the investor will be able to maintain identical position regardless of the share price.
(iii) If the risk-free rate of return is 5% p.a. for the three months period, w hat is the value of the option at the beginning of the period ?
(iv) What is the expected return on the option ? [Nov. 2019] [8 Marks]
Answer:
(i) The combination of share and option that investor should select depends on the hedge ratio (A) which can be computed as follows:
Hedge Ratio Δ = \(\frac{C_u-C_d}{\mathrm{~S}_{\mathrm{u}}-\mathrm{S}_{\mathrm{d}}}\) = \(\frac{100-0}{650-450}\) = \(\frac{100}{200}\) = 0.50
C_u = value of call option if price rises.
S_u = value of Share if price rises.
C_d = value of call option if price falls.
S_d = value of share if price falls.
The investor should take opposite positions in the share and the call option for a perfect hedge. If he is long on shares, he must sell call option. This means that for purchases of every 0.50 share, he should write 1 call option. As the price of share today is Rs. 500, he should invest Rs. 250 today and receive the call premium.

(ii) Value of Option today:

If price of share comes out to be Rs. 650 then
Value of purchased share will be (0.50 × Rs. 650)	Rs. 325
Loss on account of Short Position in call option at an exercise price of Rs. 550 (Rs.650-Rs.550)	Rs.100
Net position after three months	Rs. 225
If price of share comes out to be Rs. 450 then
Value of purchased share will be (0.50 × Rs. 450)	225
Loss on account of Short Position in call option at an exercise price of Rs. 550.	Nil
Net position after three months	Rs. 225

(iii) Therefore, Premium (P) shall be computed as follows:
(Rs. 250 – P) 1.0125 = Rs. 225
P = Rs. 27.78

(iv) Expected Return on the Option:
Expected Option Value at the time of maturity
= (Rs. 650 – 550) × 0.70 + 0 × 0.30 = Rs. 70
Expected Rate of Return = \(\frac{70-27.78}{27.78}\) × 100 = 151.98
= 152% for 3 months.

Question 5.
A call option on gold with exercise price ₹ 26,000 per ten gram and three months to expire is being traded at a premium of ₹ 1,010 per ten gram. It is expected that in three months’ time the spot price might change to ₹ 27,300 or 24,700 per ten gram. At present this option is at-the-money and the rate of interest with simple compounding is 12% per annum. Is the current premium for the option justified? Evaluate the option and comments. [Nov. 2017] [5 Marks]
Answer:
The Probability of Price going up is given by the following formula. In this formula, the probability is calculated without using continuous compounding. As the option is at- the- money, the spot price and exercise price is same ie. Rs.26,000.
P = \(\frac{R f-d}{u-d}\)
R_f = 1.03 Future value at risk free of interest after 3 months.
d = 24,700/26,000 = 0.95 (The price may go down to Rs. 24,700)
u = 27,300/26,000 = 1.05 (The price may go down to Rs. 27,300)
p = \(\frac{1.03-0.95}{1.05-0.95}=\frac{0.08}{0.10}\) = 0.80
Thus, probability of rise in price is 0.80
Premium of the option = \(\frac{1300(0.80)+0(0.20)}{1.03}\) = ₹ 1009.71 = ₹ 1010 approx.
The premium of option is ₹ 1010 which is approximately the theoretical price using simple compounding. Therefore, the current premium for the option is justified (if rounded off in multiple of ₹1).

Question 6.
The current market price of an equity share of Penchant Ltd. is ₹ 420. Within a period of 3 months, the maximum and minimum price of it is expected to be ₹ 500 and ₹ 400 respectively. If the risk free rate of interest be 8% p.a., what should be the value of a ‘3 months’ CALL option under the ‘Risk neutral’ method at the strike rate ₹ 450? Given e^0.02 = 1.0202 [May 2011] [5 Marks]
Answer:
Let the probability of attaining the maximum price be p
(500 – 420) × p + (400 – 420) × (1 – p) = 420 × (e^0.02, 1)
80p – 20 (1 – p) = 420 × 0.0202
80p – 20 + 20p = 8.48
100p = 28.48
p = 0.2848
The value of Call Option = \(\frac{0.2848 \times(500-450)}{1.0202}\) = \(\frac{0.2848 \times 50}{1.0202}\) = ₹ 13.96

Question 7.
Following information is available for X Company’s shares and Call option:

Current share price	₹ 185
Option exercise price	₹ 170
Risk free interest rate	7%
Time of the expiry of option	3 years
Standard deviation	0.18

Calculate the value of option using Black-Scholes formula.
Given In (1.0882)= 0.08455 [Nov. 2008] [12 Marks]
Answer:

= d₁ – σ√t
= 1.1006 – 0.31177 = 0.7888
N (d₁) = 0.8770 (from table)
N (d₂) = 0.7823 + 0.88 × (0.7852 – 0.7823)
= 0.7848
Value of call option = S (Nd₁) – \(\frac{X}{e^n}\) (Nd₂)
= 185 (0.8770) – \(\frac{170}{e^{0.21}}\) (07848)
= 162.245 – 108.151
= ₹ 54.094

Question 8.
A purchased a 3-month call option for 100 shares in XYZ Ltd. at a premium of ₹ 30 per share, with an exercise price of ₹ 550. He also purchased a 3 month put option for 100 shares of the same company a premium of ₹ 5 per share with an exercise price of ₹ 450. The market price of the share on the date of Mr. A’s purchase of options, is ₹ 500. Calculate the profit or loss that Mr. A would make assuming that the market price falls to ₹ 350 at the end of 3 months. [May 2010] [4 Marks]
Answer:
A call option is exercisable when strike price is less than market price and put option is exercisable if strike price is more than market price.
Since the market price at the end of 3 months falls to ₹ 350 which is below the exercise price under the Call option and the put option, the call option will not be exercised, only Put option becomes exercisable:

Question 9.
Mr. X established the following spread on the Delta Corporation’s stock:
(i) Purchased one 3-month Call option with a premium of ₹ 30 and an , exercise price of ₹ 550.
(ii) Purchased one 3-month Put option with a premium of ₹ 5 and an exercise price of ₹ 450.
Delta Corporation’s stock is currently selling at ₹ 500. Determine profit or loss, if the price of Delta Corporation’s :
(i) remains at ₹ 500 after 3 months.
(ii) falls at ₹ 350 after 3 months.
(iii) rises to ₹ 600.
Assume the size of option is 100 shares of Delta Corporation. [May 2018] [Nov. 2008, Nov. 2011] [6 Marks]
Answer:
Total premium paid on purchasing both the call and put option on 100 shares
= (₹ 30 per share × 100) + (₹ 5 per share × 100).
= 3,000 + 500 = ₹ 3,500
(i) As the price of share remains at ₹ 500, X will exercise neither the call option nor the put option. The total premium will be lost and there will be no gain on call or put option.
Therefore, Net loss = ₹ 3,500

(ii) Since the price of the stock is ₹ 350, which is below the exercise price of the call, the call will not be exercised. Only put is worth exercising.
Total premium paid = ₹ 3,500
Value at the time of expiry = -₹ 3,500 + ₹ [{450 – 350} × 100]
= – ₹ 3,500 + ₹ 10,000 = ₹ 6,500
Net gain = ₹ 6,500

(iii) In this situation, the put is worthless, since the price of the stock is Rs. 600 and is above the exercise price of the put but, call will be profitable and is exercised.
Total premium paid = ₹ 3,500
Value at the time of expiry = – 3,500 + [(600 – 550) × 100]
Net Gain = – 3,500 + 5,000 = ₹ 1,500

Question 10.
Fresh Bakery Ltd.’s share price has suddenly started moving both upward and downward on a rumour that the company is going to have a collaboration agreement with a multinational company in bakery business. If the rumour turns to be true, then the stock price will go up but if the rumour turns to be false, then the market price of the share will crash. To protect from this an investor has purchased the following call and put option:
(i) One 3 months Call with a strike price of ₹ 52 for ₹ 2 premium per share.
(it) One 3 months Put with a strike price of ₹ 50 for ₹ 1 premium per share.
Assuming a lot size of 50 shares, determine the following:
(1) The investor’s position, if the collaboration agreement push the share price to ₹ 53 in 3 months.
(2) The investor’s ending position, if the collaboration agreement fails and the price crashes to ₹ 46 in 3 months time. [May 2016 ] [5 Marks]
Answer:
Given:

Strike price of 3 month Call (X)	₹ 52	Call Premium	₹ 2
Strike price of 3 month Put (X)	₹ 50	Put Premium	₹ 1
Lot Size	50 Shares

Cost of call and put option together:
= (2 per share × 50) + (1 per share × 50)
= 150

(i) If price Increases to 53: It is higher than strike price of call. So, investor exercises it and put option will lapse. Net Position = Gain on call – Premium
= (S – X) = ( 53-52).
= (1 × 50) – 150
Net Loss = (Rs. 100)

(ii) If price decrease to 46: Here price decreases. So, call option will lapse and put option will be exercised.
Net Position = Gain on put – Premium
Gain on Put = (X – S) = (50 – 46) = 4
= (4 × 50) – 150
Net Gain = ₹ 50

Question 11.
Mr. John established the following spread on the TTK Ltd.’s stock:
(i) Purchased one 3 month put option with a premium of ₹ 15 and an exercise price of ₹ 900
(it) Purchased one 3-month call option with a premium of ₹ 90 and an exercise price of ₹ 1,100.
TTK Ltd.’s stock is currently selling at ₹ 1,000. Calculate gain or loss, if the price of stock of TTK Ltd.’s:
(i) Remains at ₹ 1,000 after 3 months.
(ii) Falls to ₹ 700 after 3 months.
(iii) Rises to ₹ 1,200 after 3 months.
Assume the size of option is 200 shares of TTK Ltd. [May 2019] [8 Marks]
Answer:
Total premium paid on purchasing both the put and call option on 200 shares
= (₹ 15 per share × 200) + (₹ 90 per share × 200).
= 3,000 + 18,000 = ₹ 21,000

(i) If the price remains at ₹ 1,000 after 3 months: As the price of share remains at ₹ 1,000, Mr. John will not exercise the call or the put option, the put option is not exercisable.
Entire premium paid will be lost
Therefore, Net loss = ₹ 21,000

(ii) If the price falls tot 700 after 3 months: Since the price of the stock is ₹ 700 which is below the exercise price of the call, the call will not be exercised. Only put is worth exercising.
Total premium paid = ₹ 21,000
Gain on put = (900 – 700) × 200 = ₹ 40,000
Ending value = – ₹ 21,000 + ₹ [{900 – 700} × 200]
= – ₹ 21,000 + ₹ 40,000 = ₹ 19,000
∴ Net gain = ₹ 19,000

(iii) If the price rises to ₹ 1,200 after 3 months: In this situation, the put is worthless, since the price of the stock is 11,200 and is above the exercise price of the put but call will be profitable and is exercised.
Total premium paid = ₹ 21,000
Gain on call = (1,200 – 1100) × 200 = ₹ 20,000
Ending value = -21,000 + [(1200 – 1100) × 200]
Net Gain = – 21,000 + 20,000 = ₹ – 1,000

Question 12.
Equity share of PQR Ltd. is presently quoted at ₹ 320. The Market Price of the share after 6 months has the following probability distribution:

A put option with a strike price of ₹ 300 can be written.
You are required to find out expected value of option at maturity (i.e. 6 months) [Nov. 2010] [5 Marks]
Answer:
Since the option is a Put option with a strike price (X) of Rs. 300, the option will be exercised only if market price falls below the strike price after 6 months.

Expected Value of Option (Put option, X = ₹ 300)

The expected value of put option with a strike price of ₹ 300, after 6 months is ₹ 30.

Question 13.
You as an investor had purchased a 4 month call option on the equity shares of X Ltd. of f 10, of which the current market price is ₹ 132 and the exercise price ₹ 150. You expect the price to range between ₹ 120 to ₹ 190. The expected share price of X Ltd. and related probability is given below:

Compute the following:
1. Expected Share price at the end of 4 months.
2. Value of Call Option at the end of 4 months, if the exercise price prevails.
3. In case the option is held to its maturity, what will be the expected value of the call option? [Nov. 2012] [8 Marks] [Nov. 2018] [8 Marks]
Answer:
1. Expected Share Price = Σx_ip_i
= ₹ 120 × 0.05 + ₹ 140 × 0.20 + ₹ 160 × 0.50 + ₹ 180 × 0.10 + ₹ 190 × 0.15
= ₹ 6 + ₹ 28 + ₹ 80 + ₹ 18 + ₹ 28.50 = ₹ 160.50

2. Intrinsic Value of Call Option if exercise price prevails ie. Rs.150 (S=X)
₹ 150 – ₹ 150 = Nil (There will be loss of Premium)

3. If the Option is held till Maturity the Expected Value of Call Option
Since the option is a Call option with a strike price (X) of Rs. 150, the option will be exercised only if market price is above the strike price after 4 months.

Expected Value of Option

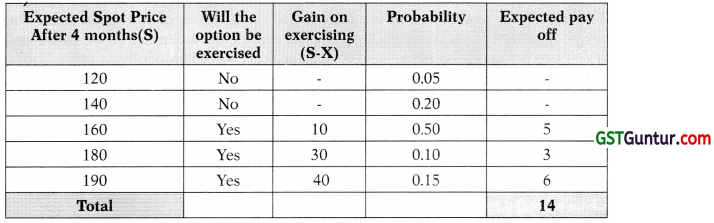
The expected value of the call option at maturity is ₹ 14.

Question 14.
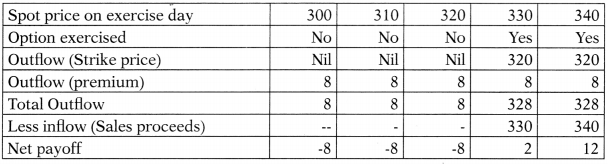
The equity share of SSC Ltd. is quoted at t 310. A three month call option is available at a premium of ₹ 8 per share and a three month put option is available at a premium of ₹ 7 per share.
Ascertain the net payoffs to the option holder of a call option and a put option, considering that:
(i) The strike price in both cases is ₹ 320; and
(ii) The share price on the exercise day is ₹ 300, 310, 320, 330 and 340.
Also indicate the price range at which the call and the put option may be gainfully exercised. [Nov. 2018] [8 Marks]
Answer:
Net pay off for the holder of the call option

Net payoff for the holder of the put option

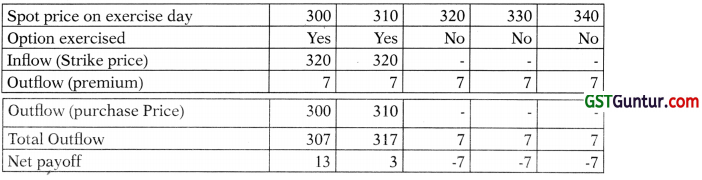
The loss of the option holder is restricted to the amount of premium paid. The profit (positive payoff) depends on the difference between the strike price and the share price on the exercise day. Call is exercisable gainfully at price above Strike price + Premium i.e. for any price over and above ₹ 320 + ₹ 8 = ₹ 328 and the put option is gainfully exercisable at any price below the Strike price – Premium i.e. any price below ₹ 320 – 7 = ₹ 313.

Question 15.
The share of X Ltd. is currently selling for ₹ 300. Risk free interest rate is 0.8% per month. A three months futures contract is selling for ₹ 312. Develop an arbitrage strategy and show what your riskless profit will be 3 months hence assuming that X Ltd. will not pay any dividend in the next three months. [May 2009] [4 Marks]
Answer:
The theoretical value of the 3 months futures contract is:
F = ₹ 300 (1.008)3 = ₹ 307.26
Since the futures is selling for Rs.312, therefore, its price exceeds its theoretical value and there can be an arbitrage profit. The following course of action will result in profits. As it is overpriced it is worth selling and to buy the share by borrowing Rs. 300.

Action	Initial Cash flow	Cash flow(after 3 flow months)
Borrow ₹ 300 now and repay with interest after 3 months	+ ₹ 300	₹ 300 (1.008) 3 = – ₹ 307.26
Buy a share now and sell the share after 3 months	– ₹ 300	Stock Price (SP)
Sell a futures contract @ Rs. 312 now Gain after 3 months	0	₹ 312-(SP)
Total	₹ 0	₹ 4.74

Such an action would produce a riskless profit of ₹ 4.74.

Question 16.
A Rice Trader has planned to sell 22000 kg of Rice after 3 months from now. The spot price of the Rice is ₹ 60 per kg and 3 months future on the same is trading at ₹ 59 per kg. Size of the contract is 1000 kg. The price is expected to fall as low as ₹ 56 per kg, 3 months hence. What the trader can do to mitigate its risk of reduced profit? If he decides to make use of future market, what would be the effective realized price for its sale when after 3 months, spot price is ₹ 57 per kg and the future contract price for 3 months is ₹ 58 per kg? [May 2019] [8 Marks]
Answer:
The trader should take short position in the Rice future contract as he fears a fall in the price. Given:

1. Particulars	₹
2. Spot Price (today)	60
3. Future trading at	59
4. Spot (after 3 months)	57
5. Future price (after 3 months)	58
6. Contract Size (Kg)	1000
7. Total quantity (Kg)	22,000

The effective realized price for its sale after 3 months:
No of future contracts sold = \(\frac{22,000}{1,000}\) = 22 contracts @ ₹ 59

After 3 months:

Particulars	Calculation	₹
Sale of 22,000 Kg rice @ prevailing spot price i.e. ₹ 57	2,000 × 57	12,54,000
Gain on future	(59 – 58) × 1000 × 22	22,000
Total amount realized		12,76,000
Effective Price (per kg)	\(\frac{12,76,000}{22,000}\)	58

Question 17.
The six months forward price of a security is ₹ 208.18. The rate of borrowing is 8 per cent per annum payable at monthly rates. What will be the spot price? [Nov. 2011] [5 Marks]
Answer:
Calculation of spot price
The formula for calculating forward price is:
F = S(1 + i)ⁿ
Where:
F = Forward price
S = Spot Price
i = Rate of interest for the period in decimals
n = Time
Using the above formula,
208.18 = S (1 +0.08/12)6
Or 208.18 = S × 1.0409 = 200 (approx.)
Hence, the spot price should be ₹ 200.

Question 18.
A future contract is available on R Ltd. that pays an annual dividend of Rs. 4 and whose stock is currently priced at Rs. 125. Each future contract calls for delivery of 1,000 shares to stock in one year, daily marking to market. The corporate treasury bill rate is 8%.
Required:
(t) Given the above information, what should the price of one future contract be?
(ii) If the company stock price decreases by 6%, what will be the price of one futures contract ?
(iii) As a result of the company stock price decrease, will an investor that has a long position in one futures contract of R Ltd. realizes a gain or loss ? What will be the amount of his gain or loss ?
(Ignore margin and taxation, if any) [Nov. 2019] [6 Marks]
Answer:
Given
Dividend (d) = Rs. 4
Stock price (S) = Rs. 125
Treasury bill rate (R_f) = 8%

(i) Theoretical future Price:
F = Se^rt
Dividend yield = \(\frac{4}{125}\) × 100 × = 3.2%
F = 125e^(Rf-d)t
125^{e(0.08-0032)(1)}
125e^0.048
e^0.048 = 1.0492
F = 125 × 1.0492 = Rs. 131.15

(ii) If the company’s stock price decreases by 6%, the future price will be:-
New Price = 125 – 6% = 117.5
Dividend yield = \(\frac{4}{117.5}\) × 100= 3.4%
Future Price(F) = 117.5e^(Rf-d)t
117.5e^{(0.08-0.034)(1)}
117.5 e^0.046
e^0.046 = 1.0471
117.5 × 1.0471 =123.03 = 123 Approx.

(iii) Inventor having long position will lose due to fall in the price of the future contract.
The amount of loss on one future Contract having 1000 shares will be.
[131.15 – 123] × 1000
= Rs. 8150

Question 19.
On 31-8-2011, the value of stock index was ₹ 2,200. The risk free rate of return has been 8% per annum. The dividend yield on this Stock Index is as under:

Month	Dividend paid
January	3%
February	4%
March	3%
April	3%
May	4%
June	3%
July	3%
August	4%
September	3%
October	3%
November	4%
December	3%

Assuming that interest is continuously compounded daily, find out the future price of contract deliverable on 31-12-2011.
Given: e^0.01583 = 1.01593 [May 2012] [5 Marks]
Answer:
The period of contract is from 1.9.2011 – 31.12-2011.
The duration of future contract is 4 months. The average/divided yield during this period will be:
\(\frac{3 \%+3 \%+4 \%+3 \%}{4}\) = 3.25%
As per Cost to Carry model the future price will be
F = Se^{(r – D)t}
Where S = Spot Price
R_f = Risk Free interest
D = Dividend Yield
t = Time Period
Accordingly, future price will be
= ₹ 2,200 e^{(0.08 – 0.0325) × \(\frac{4}{12}\)}
= ₹ 2,200 e^0.01583
= ₹ 2,200 × 1.01593.
= ₹ 2235.05.
The Future Price of the contract is ₹ 2235.05.

Question 20.
The NSE-50 Index futures are traded with rupee value being Rs. 100 per index point. On 15th September, the index closed at 1195 and December futures (last trading day December 15) were trading at 1225. The historical dividend yield on the index has been 3% per annum and the borrowing rate was 9.5% per annum.
(i) Determine whether on September 15, the December futures were underpriced or overpriced ?
(ii) What arbitrage transaction is possible to gain out this mispricing ?
(iii) Calculate the gains and losses if the index on 15th December closes at
(a) 1260 (b) 1175.
Assume 365 days in a year for your calculations. [Nov. 2019 Old Syllabus] [8 Marks]
Answer:
Given
Dividend yield = 3%
Spot price = Rs. 1195
December Future price = Rs. 1225
Borrowing rate = 9.5%

(i) Theoretical future Price:
F = Se^rt
1195e^{(0.095-0.03) × \(\frac{91}{365}\)}
= 1195 × (1.016339)
= Rs.1214.53
The December futures are overpriced, since theoretical price is Rs. 1214.53 whereas their trading at 1225.

(ii) The Arbitrageur can sell December Index Futures and Buy Nifty worth Rs. 100 per Index point by borrowing Rs. 1,19,500, i.e. (1195 × 100)

(iii) Gain or Loss If Index turns out to be at
(a) 1260

Particulars	PositionToday	Position After 3 Months
Borrow	1195	Repay after adjusting dividends	Rs. – 1214.53
Sell Dec. futures		Loss on Index	– 35 (1225-1260)
Buy Index	-1195	Sell Index	+ 1260
Total	0		10.47
Net Gain	in Points 10.47 i.e. 10.47 × 100 = Rs. 1047

(b) 1175

Borrow	1195	Repay after adjusting dividends	Rs. – 1214.53
Sell Dec. futures		Gain on Index	= + 50(1225-1275)
Buy Index	-1195	Sell Index	+ 1175
Total	0		10.47
Net Gain	in Points 10.47 i.e. 10.47 × 100 = Rs. 1047

Thus, the gain remains same irrespective of the closing price of Index Futures.

Question 21.
A company is long on 10 MT of copper @ ₹ 474 per kg (spot) and intends i to remain so for the ensuring quarter. The standard deviation of changes on its spot and future prices are 4% and 6% respectively, having correlation coefficient of 0.75.
What is its hedge ratio? What is the amount of the copper future it should short to achieve a perfect hedge? [May 2012] [5 Marks]
Answer:
The optimal hedge ratio to minimize the variance of company’s position is given by:
H = P\(\frac{\sigma S}{\sigma F}\)
Where
σS = Standard deviation of S
σF = Standard deviation of F
P = Coefficient of correlation between S and F
H = Hedge Ratio

Accordingly,
H = 0.75 × \(\frac{0.04}{0.06}\) = 0.5
No. of contract to be short = 10 × 0.5 = 5
Amount = 5,000 × ₹ 474 = ₹ 23,70,000

Question 22.
A Mutual Fund is holding the following assets in ₹ Crore:

Investments in diversified equity shares	90.00
Cash and Bank Balances	10.00
	100.00

The Beta of the portfolio is 1.1. The index future is selling at 4300 level. The Fund Manager apprehends that the index will fall at the most by 10%. How many indexed futures he should short for perfect hedging so that the portfolio beta is reduced to 1.00? One index future consists of 50 units.
Substantiate your answer assuming the Fund Manager’s apprehension will materialize. [May 2011] [5 Marks]
Answer:
As there is no risk in holding cash it is assumed that the Beta of the portfolio is not the weighted Beta but Beta of the investments in equity shares.
Number of index futures to be sold by the Fund Manager for perfect hedging is:
\(\frac{1.1 \times 90,00,00,000}{4,300 \times 50}\) = 4,604.65 = 4605 (Rounded off)
So, if the index falls by 10%
Loss in the value of the portfolio will be 1.1 × 10 = 1196
= ₹ \(\frac{11}{100}\) × 90 Crore = ₹ 9.90 Crore.
Value of index futures will be 3,870 (4,300 – 10%)
Gain on 1 index = ₹ 430 (4300- 3870)
Gain by short covering of index future is: 430 × 50 × 4,605 = 9.90075 Crore
Therefore, the loss in equity portfolio is covered by gain in future. The slight extra gain is due to the number of contracts being rounded off to 4605.

Question 23.
Ram buys 10,000 shares of X Ltd. at a price of ₹ 22 per share whose beta value is 1.5 and sells 5,000 shares of A Ltd. at a price of ₹ 40 per share having a beta value of 2. He obtains a complete hedge by Nifty futures at ₹ 1,000 each. He closes out his position at the closing price of the next day when the share of X Ltd. dropped by 2%, share of A Ltd. appreciated by 3% and Nifty futures dropped by 1.5%.
What is the overall profit/loss to Ram? [Nov. 2013] [6 Marks]
Answer:
Given initial position:

Cash Outlay
= ₹ 10,000 × ₹ 22 – ₹ 5,000 × ₹ 40
= 2,20,000 – ₹ 2,00,000
= ₹ 20,000
Net exposure considering Beta
₹ 2,20,000 × 1.5 – ₹ 2,00,000 × 2 = – 70,000
Future Contract should be bought, since net position is short.
No. of future contracts to be bought to get perfect hedge.
= \(\frac{70,000}{\text { Rs. } 1,000}\)
= 70 contracts
Position after long on Futures:

Cash Outlay after hedging through future
= 20,000 + 70,000
= ₹ 90,000
Cash Inflow at Close Out
= ₹ 2,20,000 × 0.98 – ₹ 2,00,000 × 1.03 + ₹ 70,000 × 0.985
= ₹ 2,15,600 – ₹ 2,06,000 + ₹ 68,950
= ₹ 78,550
Loss
= ₹ 78,550 – ₹ 90,000 = ₹ (11,450)

Question 24.
A textile manufacturer has taken floating interest rate loan of ₹ 40,00,000 on 1st April, 2012. The rate of interest at the inception of loan is 8.5% p.a. Interest is to be paid every year on 31st March, and the duration of loan is four years. In the month of October 2012, the Central Bank of the country releases following projections about the interest rates likely to prevail in future.
(i) On 31st March, 2013, at 8.75%, on 31st March, 2014 at 10%, on 31st March, 2015 at 10.5% and on 31st March, 2016 at 7.75%, Show how this borrower can hedge the risk arising out of expected rise in the rate of interest when he wants to peg his interest cost at 8.50% p.a.
(ii) Assume that the premium negotiated by both the parties is 0.75% to be paid on 1st October, 2012 and the actual rate of interest on the respective due dates happens to be as : on 31st March 2013 at 10.2%; on 31st March 2014 at 11.5%; on 31st March, 2015 at 9.25%, on 31st March, 2016 at 8.25%. Show how the settlement will be executed on the prospective interest due dates? [Nov. 2017] [8 Marks]
Answer:
It is assumed that Interest rate on the loan will be prevailing rate on the date of payment.
To hedge the risk arising out of expected rise in the rate of interest, the Textile Manufacturer can enter into Interest Rate Cap contract at a strike rate of 8.50% p.a.
Hence, he can freeze the Interest cost at 8.50%. Since the issues will be reimbursed by the cap deals.
Premium to be paid on 1.10.2012
= 40,00,000 × 0.75%
= 30,000

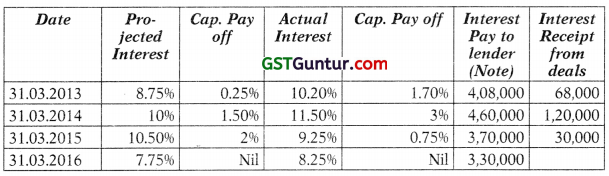
Note:
Interest = ₹ 40,00,000 × Int. Rate %.
Interest Payment is based on Actual Rate and Receipt is based on Cap-pay off.

Question 25.
On January 1, 2013 and investor has a portfolio of 5 shares as given below:

Security	Price	No. of Shares	Beta
A	349.30	5,000	1.15
B	480.50	7,000	0.40
C	593.52	8,000	0.90
D	734.70	10,000	0.95
E	824.85	2,000	0.85

The cost of capital to the investor is 10.5% per annum.
You are required to calculate:
(i) The beta of his portfolio.
(ii) The theoretical value of NIFTY Futures
(iii) The number of contracts of NIFTY the investor needs to sell to get a full hedge until February for his portfolio if the current value of NIFTY is 5900 and NIFTY futures have a minimum trade lot requirement of 200 units. Assume that the futures are trading at their fair value.
(iv) The number of future contracts the investor should trade if he desires to reduce the beta of his portfolios to 0.6.
No. of days in a year be treated as 365.
Given: In (1.105) = 0.0998
e^(o.o15858) = 1.01598 [May 2013] [8 Marks]
Answer:
(i) Computation of Portfolio Beta

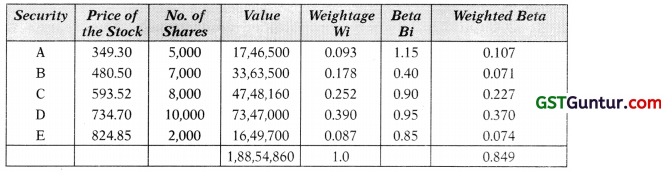
Portfolio Beta = 0.849

(ii) Computation of Theoretical Value of Future Contract
Cost of Capital = 10.5% p.a. Accordingly, the Continuously Compounded
Rate of Interest In (1.105) = 0.0998
For February 2013 contract, t = 58/365 = 0.1589
Further F = Sert
F = ₹ 5,900 e^{(0.00998)(0.1589)}
F = ₹ 5,900 e^0.015858
F = 5,900 × 1.01598 = ₹ 5,994.28

(iii) When total portfolio is to be hedged:
= \(\frac{\text { Value of Spot Position requiring hedging }}{\text { Value of Future Contract }}\) × Portfolio Beta
= \(\frac{1,88,54,860}{5994.28 \times 200}\) × 0.849 = 13.35 contracts rounded off to 14 contracts (as full hedge is needed)

(iv) When total portfolio beta is to be reduced to 0.6:
Number of Contracts to be sold = \(\frac{P\left(\beta_p-\beta_p\right)}{F}\)
= \(\frac{1,88,54,860(0.849-0.600)}{5994.28 \times 200}\) = 3.92 contracts ~ 4 contracts

Question 26.
On April 1, 2019, Kasi has a portfolio consisting of four securities as shown below:

Cost of Capital is 16% p.a. compounded continuously. Kasi fears a fall in prices of shares in future. Accordingly, he approaches you for the advice to protect the interest of his Portfolio.
You can make use of the following information:
(i) The current NIFTY Value is 9380.
(ii) NIFTY Futures can be traded in units of 25 only.
(iii) Futures for September are currently quoted at 9540 and Futures for October are being quoted at 9820.
You are required to calculate:
1. The Beta of his Portfolio.
2. Theoretical Value of Futures for contracts expiring in September & October.
Given (e^0.067 = 1.0693, e^0.08 = 1.0833, e^0.093 = 1.0975)
3. The number of NIFTY Contract that he would have to sell, if he desires to hedge 150% of the Portfolio until October. [May 2019] [5 Marks]
Answer:
(1) Beta of the Portfolio

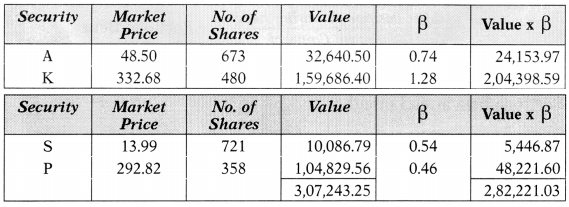
Portfolio Beta = \(\frac{\text { Rs.2,82,221.03 }}{\text { Rs.3,07,243.25 }}\) = 0.9186 say 0.92

(2) Theoretical Value of Future Contract Expiring in September and October
F = Se^rt
F. = 9380 × e^{o.16 × (6/12)} = 9380 × e^o.o8
According the price of the September Contract
9380 × 1.0833 = Rs. 10,161.35
Price of the October Contract
F_Oct = 9380 × e^{0.16 × (7/12)} = 9380 × e^0.093
= 9380 × 1.0975 = Rs. 10,294.55

(3) No. of NIFTY Contract to be sold to hedge 150% of Portfolio
Value of Portfolio = Rs. 3,07,243.25
150% of Portfolio = Rs. 3,07,243.25 × 1.50 = Rs. 4,60,864.88
No. of Contracts to Hedge = \(\frac{\text { Rs. } 4,60,864.88}{9820 \times 25}\) × 0.92 = 1.73 contracts say 2 contracts.

Question 27.
A trader is having in its portfolio shares worth ₹ 85 lakhs at current price and cash ₹ 15 lakhs. The beta of share portfolio is 1.6. After 3 months the price of shares dropped by 3.2%.
Determine:
(i) Current portfolio beta.
(ii) Portfolio beta after 3 months if the trader on current date goes for long position on ₹ 100 lakhs NIFTY futures. [Nov. 2013] [5 Marks]
Answer:
Current portfolio
Current Beta for share = 1.6
Beta for cash = 0
Current portfolio beta = 0.85 × 1.6 + 0.15 = 1.36
Portfolio beta after 3 months:
Beta tor portfolio of shares = \(=\frac{\text { Change in value of portfolio of share }}{\text { Change in value of market portfolio (Index) }}\)
1.6 = \(\frac{0.032}{\text { Change in value of market portfolio (Index) }}\)
Change in value of market portfolio (Index) = (0.032/1.6) × 100 = 2%
Position taken on 100 lakh NIFTY futures : Long
Value of index after 3 months = ₹ 100 lakh × (100 – 0.02)
= ₹ 98 lakh
Loss on future paid = ₹ 2 lakh
Cash balance after payment of loss = ₹ 13 lakh (₹ 15 lakhs – ₹ 2 lakhs)
Value of portfolio after 3 months = ₹ 85 lakh (1 – 0.032) + ₹ 13 lakh = ₹ 95.28 lakh
Change in value of portfolio = \(=\frac{R s .100 l a k h-R s .95 .28 \mathrm{lakh}}{R s .100 \mathrm{lakh}}\)
= 4.72%
Portfolio beta = 0.0472/0.02 = 2.36

Question 28.
On April 1, 2015, an investor has a portfolio consisting of eight securities as shown below:

Security	Market Price	No. of Shares	β Value
A	29.40	400	0.59
B	318.70	800	1.32
C	660.20	150	0.87
D	5.20	300	0.35
E	281.90	400	1.16
F	275.40	750	1.24
G	514.60	300	1.05
H	170.50	900	0.76

The cost of capital for the investor is 20% p.a. continuously compounded. The investor fears a fall in the prices of the shares in the near future. Accordingly, he approaches you for the advice to protect the interest of his portfolio.
You can make use of the following information:
(i) The current NIFTY value is 8500.
(ii) NIFTY futures can be traded in units of 25 only.
(iii) Futures for May are currently quoted at 8700 and Futures for June are being quoted at 8850.
You are required to calculate:
(i) The beta of his portfolio
(ii) The theoretical value of the futures contract for contracts expiring in May and June.
Given (e^0.03 = 1.03045, e^0.04 = 1.04081, e^0.05 = 1.05127)
(iii) The number of NIFTY contracts that he would have to sell if he desires to hedge until June in each of the following cases:
(a) His total portfolio
(b) 50% of his portfolio
(c) 120% of his portfolio [Nov. 2015] [8 Marks]
Answer:
(i) The beta of his Portfolio:
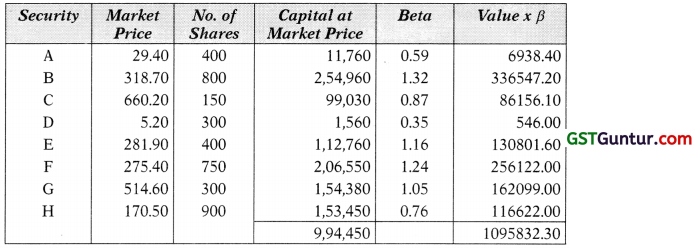g
Portfolio Beta = \(\frac{10,95,832.30}{9,94,450}\) = 1.102

(ii) Theoretical Value of Future Contract Expiring in May and June
F = Se^rt
F_May = 8500 × e^{0.20 × (2/12)} = 8500 × e^0.0333
e^0.0333 shall he computed using Interpolation Formula as follows:

e0.03	= 1.03045
e0.04	= 1.04081
e0.01	= 0.01036
e0.0033	= 0.00342

e^0.0333 = 1.03045 + 0.00342 = 1.03387.
According the price of the May Contract
8500 × 1.03387 = ₹ 8,788
Price of the June Contract.
F_June = 8500 × e^{0.20 × (3/12)} = 8,500 × e^0.05 = 8,500 × 1.05127 = 8935.80

(iii) ) No. of NIFTY Contracts required to sell to hedge until June
= \(=\frac{\text { Value of Position to be hedged }}{\text { Value of Future Contract }}\) × β
(A) Total portfolio
\(\frac{994450}{8850 \times 25}\) × 1.102 = 4.953 ~ 5 contracts

(B) 50% of portfolio
\(\frac{994450 \times 0.50}{8850 \times 25}\) × 1.102 = 2.47 ~ 3 contracts

(C) 120% of portfolio
\(\frac{994450 \times 1.20}{8850 \times 25}\) × 1.102 = 5.94 ~ 6 contracts

Question 29.
A is an investor and having in its Portfolio Shares worth ₹ 1,20,00,000 at current price and Cash ₹ 10,00,000. The Beta (p) of Shares Portfolio is 1.4. After four months the price of shares dropped by 1.8%.
You are required to determine:
(i) Current Portfolio Beta and
(ii) Portfolio Beta after four months – if A on current date goes for long position on ₹ 1,30,00,000 NIFTY futures.
Show calculations in ₹ lakhs with four decimal points. [May 2017] [5 Marks]
Answer:
(i) Calculation of Current Portfolio beta
β_portfolio = (W_shares × β_shares) + (W_cash × β_cash)
= \(\left(\frac{120}{130} \times 1.4\right)+\left(\frac{10}{130} \times 0\right)\)
= 1.29

(ii) Calculation of Portfolio beta after 4 months
Amount of action in index futures = Value of Portfolio × Increase in Beta
1,30,00,000 = (1,20,00,000 + 10,00,000) × Increase in Beta
∴ Increase in Beta = 1
∴ Beta after 4 months =1.29 + 1
= 2.29