Interest Rate Risk Management – CA Final SFM Study Material

Interest Rate Risk Management – CA Final SFM Study Material is designed strictly as per the latest syllabus and exam pattern.

Interest Rate Risk Management – CA Final SFM Study Material

Question 1.
Write short note on Interest swap [May 2012] [4 Marks]
Answer:
It is the most common type of swap agreement. An interest rate SWAP is a financial contract between two parties exchanging or swapping a stream of interest payments on a notional principal amount periodically e.g. quarterly, half-yearly, etc. during a specified period. Such contracts generally involve the exchange of a fixed-to-floating or floating rate with one base-to-floating rate with different base of interest. Accordingly, on each payment date that occurs during the SWAP period, a cash payment based on the differential between fixed and floating interest rates is made out by one party involved in the contract to another party. The financial intermediaries, such as banks, pension funds, and insurance companies, as well as non-financial firms use interest rate swaps to effectively change the maturity of outstanding debt or that of an interest-bearing asset.

Question 2.
Explain the meaning of the following relating to swap transactions:
(i) Plain Vanilla Swaps
(ii) Basis Rate Swaps
(iii) Asset Swaps
(iv) Amortizing Swaps [May 2015] [4 Marks]
Answer:
(i) Plain Vanilla Swaps: The Plain Vanilla SWAPS are most often used interest rate SWAP. It is an agreement between two parties, in which each contracts to make payment to the other on particular dates in the future till a specified termination date. One party, known as the fixed rate payer, makes fixed payments all of which are determined at the outset. The other party, known as the floating rate payer will make payments depending upon the future evolution of a specified interest rate index.

(ii) Basis Rate Swaps: It is similar to plain Vanilla SWAP with the difference that the payments are based on the difference between two different variable rates. For example, one rate may be 6 months LIBOR and the other may be PLR. In other words, two legs of SWAPS are floating but measured against different benchmark or index.

(iii) Asset Swaps: It is similar to a plain vanilla SWAP, with the main difference being the underlying. It is the exchange of fixed rate investments such as bonds which pay a guaranteed coupon rate with floating rate investments such as an index.

(iv) Amortizing Swaps: An exchange of cash flows, one of which pays a fixed rate of interest and one of which pays a floating rate of interest, and both of which are based on a notional principal amount that decreases. In an amortizing-swap, the notional principal decreases periodically because it is tied to an underlying financial instrument with a declining (amortizing) principal balance, such as a mortgage. These are particularly useful for borrowers who have issued redeemable bonds or debentures. It enables them to hedge interest rate with redemption profile of bonds or debentures.

Part-2(Numerical Problems: Topic Wise in Chronological Order)

Question 1.
TM Fincorp has bought a 6 × 9 Rs. 100 crores Forward Rate Agreement (FRA) at 5.25%. On fixing date reference rate i.e. MIBOR turns out be as follows:

Period	Rate (%)
3 months	5.50
6 months	5.70
9 months	5.85

You are required to determine:
(a) Profit/Loss to TM Fincorp in terms of basis points.
(b) The settlement amount.
(Assume 360 days in a year) [Nov. 2008] [12 Marks]
Answer:
(a) Determination of Profit /Loss to TM Fincorp
Interest under FRA = 5.25%
Actual Interest Rate (at fixing date) = 5.5%
Status: TM has taken loan for 3 months
Profit to TM = 0.25% of loan amount for 3 months
= 0.25% of Rs. 100 Crores
= 100 × .25/100 × 90 days/360 days = Rs. 6.25 Lakhs

(b) Determination of the settlement account:
The settlement amount shall be the present value of interest differential using prevailing rate of interest as discount rate.
Settlement account = \(\frac{\text { Rs. } 6.25}{1+\left(\frac{5.5}{100} \times \frac{90}{360}\right)}\) = Rs. 6,17,284

Alternative Formula:
It may be calculated directly using the following formula:
= \(\frac{(\mathrm{N})(\mathrm{RR}-\mathrm{FR})(\mathrm{dtm} / \mathrm{DY})}{[1+\mathrm{RR}(\mathrm{dtm} / \mathrm{DY})]}\)
Where,
N = The notional principal amount of the agreement;
RR = Reference Rate for the maturity specified by the contract prevailing on the contract settlement date.
FR = Agreed-upon Forward Rate; and
dtm = Maturity of the forward rate, specified in days (FRA Days)
DY = Day count basis applicable to money market transactions which could be 360 or 365 days.

Settlement Amount
= \(\frac{100 \text { Crores }(5.5 \%-5.25 \%)(90360)}{1+0.055(90360)}\)
Note: If exact dates are given, then actual number of days shall be taken. In above question, 92 days may also be taken.

Question 2.
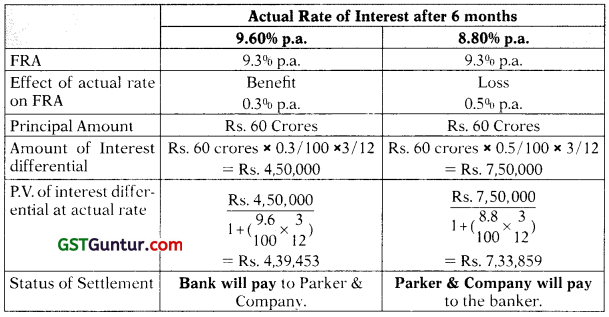
M/s. Parker & Co. is contemplating to borrow an amount of ? 60 crores for a period of 3 months in the coming 6 months’ time from now. The current rate of interest is 9% p.a., but it may go up in 6 months’ time. The company wants to hedge itself against the likely increase in interest rate.
The Company’s Bankers quoted an FRA (Forward Rate Agreement) at 9.30% p.a.
What will be the effect of FRA and actual rate of interest cost to the company, if the actual rate of interest after 6 months happens to be
(i) 9.60% p.a. and (ii) 8.80% p.a.? [May 2013] [8 Marks]
Answer:

Alternative Solution:
The final settlement amount may be computed by using formula:

(a) When actual rate of interest after 6 months happens to be 9.60%
= \(\left(\frac{₹ 60 \text { crores) }(0.096-0.093)(3 / 12)}{[1+0.096(3 / 12)]}\right)\)
= \(\frac{(₹ 60 \text { crores })(0.00075)}{1.024}\)
= ₹ 4,39.453
Therefore, banker will pay Parker & Co. a sum ₹ 4,39,453

(b) When actual rate of interest after 6 months happens to be 8.80%
= \(\frac{(₹ 60 \text { crores })(0.088-0.093)(3 / 12)}{[1+0.088(3 / 12)]}\)
= \(\frac{(₹ 60 \text { crores })(-0.00125)}{1.022}\) = ₹ 7,33,855
Therefore, Parker & Co. will pay banker a sum ₹ 7,33,855

Question 3.
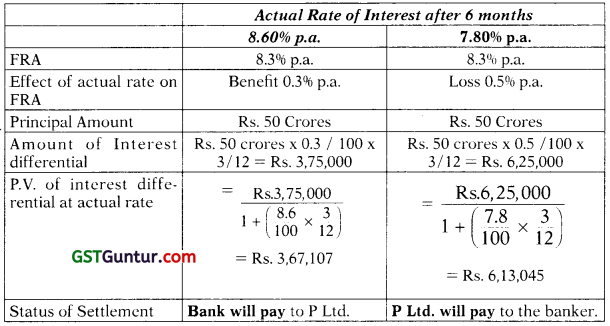
P Ltd. is contemplating to borrow an amount of Rs. 50 crores for a period of 3 months in the coming 6 months time from now. The current rate of interest is 8% per annum but it may go up in 6 months time. The company wants to hedge itself against the likely increase in interest rate.
The Company’s Bankers quoted an FRA (Forward Rate Agreement) at 8.30% per annum.
Compute the effect of FRA and actual rate of interest cost to the company, if the actual rate of interest during consideration period happens to be (i) 8.60% p.a., or (ii) 7.80% p.a.
(Show your workings on the basis of months) [Nov. 2019] [8 Marks]
Answer:
Status of P Ltd. FRA Bought (Loan to be taken)

Alternative Solution:
The final settlement amount may be computed by using formula:
(a) When actual rate of interest after 6 months happens to be 8.60%
= \(\left(\frac{(\text { Rs.50 crores })(0.086-0.083)(3 / 12)}{[1+0.086(3 / 12)]}\right)\)
= \(\frac{(\mathrm{Rs} .50 \text { crores) }(0.00075)}{1.0215}\) = Rs. 3,67107
Therefore, banker will pay P Ltd. a sum Rs. 3,67,107

(b) When actual rate of interest after 6 months happens to be 7.80%
= \(\frac{(\text { Rs. } 50 \text { crores })(0.078-0.083)(3 / 12)}{[1+0.078(3 / 12)]}\)
= \(\frac{(\text { Rs. } 50 \text { crores) }(-0.00125)}{1.0195}\) = Rs. 6,13,045
Therefore, P Ltd. will pay banker a sum Rs. 6,13,045.

Question 4.
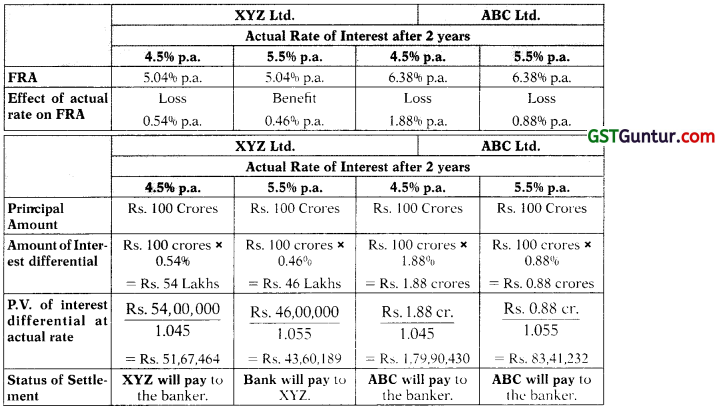
Two companies ABC Ltd. and XYZ Ltd. approach the DEF Bank for FRA (Forward Rate Agreement). They want to borrow a sum of Rs. 100 crores after 2 years for a period of 1 year. Bank has calculated Yield Curve of both companies as follows:

Year	XYZ Ltd.	ABC Ltd.
1	3.86	4.12
2	4.20	5.48
3	4.48	5.78

The difference in yield curve is due to the lower credit rating of ABC Ltd. compared to XYZ Ltd.
(i) You are required to calculate the rate of interest DEF Bank would quote under 2V3 FRA, using the company’s yield information as quoted above.
(ii) You are required to calculate the settlement amount if interest rate in 2 years turns out to be
(a) 4.50%
(b) 5.50% [Nov. 2008, Modified] [12 Marks]
Answer:
Computation of Forward Rates:
Since the FRA is not given directly in the question, it will be calculated using 1 year forward rate after 2 years in the following manner:

FOR XYZ	FOR ABC
(1.042)2 (1 + F) = (1 + 0448)3 F = \(\frac{(1.0448)^3}{(1.042)^2}\) – 1 = 0.0504 = 5.04%	(1.0548)2 (1 + F) = (1 + 0578)3 F = \(\frac{(1.0578)^2}{(1.0578)^2}\) – 1 = 0.0638 = 6.38%

Computation of settlement Amount (FRA Bought since Loan to be taken)

Question 5.
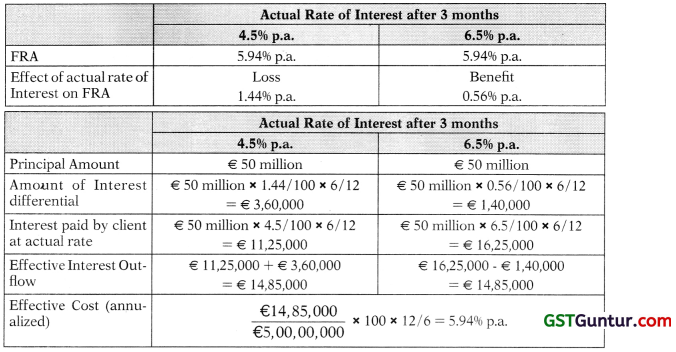
Electra space is consumer electronics wholesaler. The business of the firm is highly seasonal in nature. In 6 months of a year, firm has a huge cash deposits and especially near Christmas time and other 6 months firm cash crunch, leading to borrowing of money to cover up its exposures for running the business.
It is expected that firm shall borrow a sum of € 50 million for the entire period of slack season in about 3 months.
A Bank has given the following quotations:

Spot	5.50% – 5.75%
3 × 6 FRA	5.59% – 5.82%
3 × 9 FRA	5.64% – 5.94%

3 month ∈ 50,000 future contract maturing in a period of 3 months is quoted at 94.15 (5.85%).
You are required to determine:
(a) How a FRA, shall be useful if the actual interest rate after 3 months turnout to be:
(i) 4.5% (ii) 6.5%
(b) How 3 months Future contract shall be useful for company if interest rate turns out as mentioned in part (a) above. [Nov. 2008] [12 Marks]
Answer:
As Electra space has to borrow after 3 months for 6 months, it will buy a 3 × 9 FRA and the borrowing rate of 5.94% will be applicable.

Status of Electra space: FRA Bought (Loan to be taken)

(b) Since firm is a borrower it will like to off-set interest cost by profit on Future Contract. Accordingly, if interest rate rises it will gain hence it should sell interest rate futures.

The final outcome in the given two scenarios shall be as follows:

Future Course Action:	If the interest rate turns out to be 4.5%	If the interest rate turns out to be 6.5%
Sell to open	94.15	94.15
Buy to close	95.50(100-4.5)	93.50 (100-6.5)
Loss/ (Gain)	1.35%	(0.65%)
Cash Payment (Receipt) for Future Settlement	€ 50,000 × 2000 × 1.35% × 3/12 = €337,500	€ 50,000 × 2,000 × 0.65% × 3/12 = (€ 162,500)
Interest for 6 months on € 50 million at actual rates	€ 50 million × 4.5% × 1/2 = €11,25,000	€ 50 million × 6.5% × 1/2 = € 16,25,000
	€1,462,500	€ 1,462,500

Thus, the firm locked itself in interest rate \(\frac{€ 1,462,500}{€ 50,000,000}\) × 100 \(\frac{12}{6}\) = 5.85%

Question 6
Suppose a dealer quotes ‘All-in-cost’ for a generic swap at 8% against six
months LIBOR flat. If the notional principal amount of swap is Rs. 5,00,000.
(i) Calculate semi-annual fixed payment..
(ii) Find the first floating rate payment for (i) above lithe six months period from the effective date of swap to the settlement date comprises 181 days and that the corresponding LIBOR was 6% on the effective date of swap.
(iii) In (ii) above, if the settlement is on ‘Net’ basis, how much the fixed rate payer would pay to the floating rate payer?
Generic swap is based on 30/360 days basis. [Nov. 2008] [3 Marks]
Answer:
(i) Semi-annual fixed payment
= (N) (AIC) Period)
N = Notional Principal amount = Rs. 5,00,000
AIC = All-in-cost = 8%
Period = Swap period (Six month)
Semi-annual fixed payment = 5,00,000 × 0.08 × 180/360
= 5,00,000 × 0.08 × 0.5
= Rs. 20,000

(ii) Floating Rate Payment
= N (LIBOR) \(\left(\frac{\text { Days }}{360}\right)\) = 5,00,000 (6%) \(\left(\frac{181}{360}\right)\) = 5,00,000 × 0.060 (0.503)
= Rs. 15,090

(iii) Net Amount
(a) Fixed rate payment under semi-annual payment = Rs. 20,000
(b) Floating rate payment is Rs. 15,090.
Therefore, the fixed rate payer has to make the payment to the floating rate payer. The amount to be paid is:
= Rs. 20,000 – Rs. 15,090 = Rs. 4,910

Question 7.
A dealer quotes ‘All-in-cost’ for a generic swap at 8% against six months LIBOR flat. If the notional principal amount of swap is Rs. 6,00,000.
(i) Calculate semi-annual fixed payment.
(ii) Find the first floating rate payment for (i) above if the six months period from the effective date of swap to the settlement date comprises 181 days and that the corresponding LIBOR was 6% on the effective date of swap.
(iii) In (ii) above, if the settlement is on ‘Net’ basis, how much the fixed rate payer would pay to the floating rate payer?
Generic swap is based on 30/360 days basis. [Nov. 2010] [3 Marks]
Answer:
(i) Semi-annual fixed payment
= (N) (AIC) period)
Where
N = Notional Principal amount = Rs. 6,00,000
AIC = All-in-cost = 8%
Period = Swap period (6 month)
Semi-annual fixed payment = 6,00,000 × 0.08 × 180/360
= 6,00,000 × 0.08 × 0.5
= Rs. 24,000

(ii) Floating Rate Payment
= N(LIBOR) \(\left(\frac{\text { Days }}{360}\right)\) = 6,00,000 × 0.06 × 181/360
= 6,00,000 × 0.06 × 0.502777
= Rs. 18,100

(iii) Net Amount
(a) Fixed rate payment under semi-annual payment= Rs. 24,000
(b) Floating rate payment is Rs. 18,100.
Therefore, the fixed rate paver has to make the payment to the floating rate payer. The amount to be paid is:
= Rs. 24,000 – Rs. 18,100 = Rs. 5,900

Question 8.
A dealer quotes ‘All-in-cost’ for a generic swap at 6% against six month LIBOR flat. If the notional principal amount of swap is Rs. 8, 00,000
(i) Calculate semi-annual fixed payment.
(ii) Find the first floating rate payments for (i) above if the six month period from the settlement date comprises 181 days and that the corresponding LIBOR was 5% on the effective date of swap.
(i) In (ii) above, if the settlement is on ‘Net’ basis, how much the fixed rate payer would pay to the floating rate payer? Generic swap is based on 30/360 days basis. [May 2018] [4 Marks]
Answer:
Semi-annual fixed payment
= (N) (AIC) Period)
Where
N = Notional Principal amount = Rs. 8,00,000
AIC = All-in-cost = 6%
Semi-annual fixed payment = 8,00,000 × 0.06 × 180/360
= 8,00,000 × 0.06 × 0.5
= Rs. 24,000

(ii) Floating Rate Payment
= N(LIBOR) \(\left(\frac{\text { Days }}{360}\right)\) = 8,00,000 × 0.05 × 181/360
= 8,00,000 × 0.05 × 0.502777 = Rs. 20,111.11

(iii) Net Amount
(a) Fixed rate payment under semi-annual payment = Rs. 24,000
(b) Floating rate payment is Rs. 20,111.11
Therefore, the fixed rate payer has to make the payment to the floating rate player. The amount to be paid is:
= Rs. 24,000 – Rs. 20,111.11 = Rs. 3,888.88 or Rs. 3,889 app.

Question 9.
Derivative Bank entered into a plain vanilla swap through an OIS (Over-night Index Swap) on a principal of Rs. 10 crores and agreed to receive MI-BOR overnight floating rate for a fixed payment on the principal. The swap was entered into on Monday, 2nd August, 2010 and was to commence on 3rd August, 2010 and run for a period of 7 days.
Respective MIBOR rates for Tuesday to Monday were:
7.75%, 8.15%, 8.12%, 7.95%, 7.98%, 8.15%
If Derivative Bank received ^ 317 net on settlement, calculate fixed rate and interest under both legs.
Notes:
(i) Sunday is Holiday.
(ii) Work in rounded rupees and avoid decimal working. [Nov. 2010] [8 Marks]
Answer:

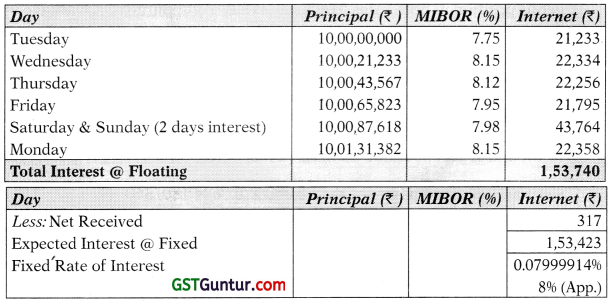
Since the bank has received Rs. 317 and the arrangement was that bank will pay at fixed rate and receive floating rate. Therefore, the floating payment is Rs. 317 more than fixed, as net payment has been made by the floating party to the bank. Hence,
Floating Rate Interest – Fixed Rate Interest = Rs. 317
Fixed Rate Interest = Floating Rate Interest – Rs. 317
= Rs. 1,53,740 – Rs. 317 = Rs. 1,53,423
Fixed number of days = 7
Notional Principal = Rs. 10 Crores
Rate of interest for 7 days = (1,53,423/10,00,00,000) × 100 = 0.153423%
Annualized Rate of interest = (0.153423/7) × 365 = 8% p.a.

Question 10.
IM is an American firm having its subsidiary in Japan and JI is a Japanese firm having its subsidiary in USA. They face the following interest rates:

Company	IM	JI
USD floating rate	Libor + 0.5%	Libor + 2.5%
JPY fixed rate	4%	4.25%

IM wishes to borrow USD at floating rate and JI JY at fixed rate. The amount required by both the companies is same at the current Exchange Rate. A financial institution requires 75 basis points as commission for arranging swap. The companies agree to share the benefit/loss equally.
You are required to find out
(i) Whether a beneficial swap can be arranged?
(ii) What rate of interest for both IM and JI? [May 2019][8 Marks]
Answer:
(i) IM has overall strong position and hence is in a comparative advanta-geous position in both rates. However, it has a comparative advantage in floating-rate market.
The differential between the U.S. dollar floating rates is 2.00% per annum, and the differential between the JPY fixed rates is 0.25% per annum. The difference between the differentials is 1.75% per annum. The total potential gain to all parties from the swap is therefore 1.75% per annum, or 175 basis points. If the financial intermediary requires 75 basis points, each of IM and JI can be made 50 basis points better off.

(ii) Since the Net Benefit of 100 Basis Points to be shared equally among IM and JI interest rate for them shall be as follows:
IM

Borrowing from Market	LIBOR + 0.5%
Less: Benefit from Swap	0.5%
Net Interest	LIBOR

JI

Borrowing from Market	4.25%
Less: Benefit from Swap	0.5%
Net Interest	3.75%

Question 11.
XYZ Limited borrows £ 15 Million of six months LIBOR + 10.00% for a period of 24 months. The company anticipates a rise in LIBOR, hence it proposes to buy a Cap Option from its Bankers at the strike rate of 8.00%.
The lump sum premium is 1.00% for the entire reset periods and the fixed rate of interest is 7.00% per annum. The actual position of LIBOR during the forthcoming respect period is as under:

Reset	Period LIBOR
1	9.00%
2	9.50%
3	10.00%

You are required to show how far interest rate risk is hedged through Cap Option.
For calculation, work out figures at each stage up to four decimal points and amount nearest to £. It should be part of working notes. [May 2013] [5 Marks]
Answer:
The premium payable to bank will be 1% of the loan amount of 15 million which shall be amortized over the period of the loan in 4 equal semi-annual instalments discounted at the rate of 7% p.a.
Premium = 1% of £15 million i.e. 0.15 million = £1,50,000
Calculation of Amortized amount(X):
1,50,000 = X multiplied by PVIFA_(35%4)
Therefore, X = \(\frac{£ 1,50,000}{3.673}\) = £ 40,838

Table showing the effect of CAP on interest cost to XYZ Limited

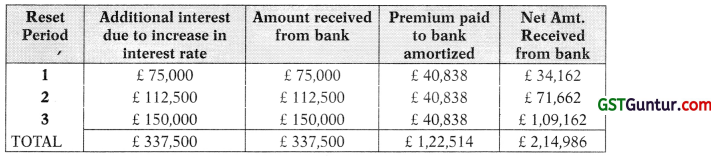
Therefore, by using the Cap Option, the interest rate amount of £ 337,500 has been reduced by £ 214,986.