Probability – CA Foundation Statistics Solutions

This Probability – CA Foundation Statistics Notes is designed strictly as per the latest syllabus and exam pattern.

Probability – CA Foundation Statistics Notes

Experiment:- The performance which produces the certain results is called Experiment.

Random Experiment:- If the results of the experiment depend on chance only, then the experiment is called Random Experiment. Example:- Tossing a coin; Throwing a die ; drawing a card from well – shuffled pack of 52 cards etc.

Sample Space:- The set of all possible distinct outcomes of a random experiment is called SAMPLE SPACE (or Event Space). It is denoted by capital letter “S”.

Ex-1 ; A coin is tossed at random then S = {H, T} ⇒ n(S) = 2
Either Head (H) or Tail (T) can occur on upper face of the coin.

Ex-2 : A die is thrown at random then S = {1, 2, 3,4, 5, 6} ⇒ n(S) = 6
∵ A die has 6 faces with face number 1, 2, 3, 4, 5, 6. One of them can occur at a time.

Ex-3 : Two coins are tossed together then S = {HH, HT; TH; TT} i.e. If both coins are tossed together then heads on both coins or Tails on both coins or Head on one coin and Tail on another one coin can occur. Another way to find Sample Space.

Total Sample Space “S” = cross – product of individual Sample – Space.
S = {H, T} × {H, T}
= {H H, HT, TH, TT}
n(S) = n(S₁) . n(S₂) = 2 × 2 = 4
Tricks : For Coins n(S) = 2^{N0. of coins tossed together}
Ex-1 For 2 coins
n(S) = 2² = 4
Ex-3. For 3 coins tossed together
n(S) = 2³ = 8.
For Dice

Ex-: If two dice are thrown together then, S = {1, 2, 3, 4, 5, 6} × {1, 2, 3, 4, 5, 6} = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6);
(2, 1), (2, 2), ………. ; (2, 3);
(3, 1), (3, 2); ……… ;(3, 6);
(4, 1), (4, 2); ……… ;(4, 6);
(5, 1), (5, 2); ……… ; (5, 6);
(6, 1), (6, 2); ……… ; (6, 6)}
∴ n(s) = n(s₁). n(s₂) = 6 × 6 = 36.
Tricks: For Dice
n(S) = 6^{No. of dice Thrown together}

Previous Year Exam Questions

Question 1.
A letter is taken out at random from the word RANGE and another is taken out from the word PAGE. The probability that they are the same letters is : [1 Mark, Nov. 2006]
(a) 1/20
(b) 3/20
(c) 3/5
(d) 3/4
Solution:
(b) 3/20

Letters A ; G ; E are common.
Total probability for each Letter in both words
= \(\frac{1}{5}\) × \(\frac{1}{4}\) + \(\frac{1}{5}\) × \(\frac{1}{4}\) + \(\frac{1}{5}\) × \(\frac{1}{4}\) = \(\frac{3}{20}\)

Question 2.
An urn contains 9 balls two of which are red, three blue and four black. Three balls are drawn at random. The probability that they are of same colour is:
(a) \(\frac{3}{27}\)
(b) \(\frac{20}{31}\)
(c) \(\frac{5}{84}\)
(d) None
Solution:
(c) \(\frac{5}{84}\) = 84 ways
E = Event same colour
n(S) = ³C₃ + ⁴C₃ = 1 + 4 = 5
(Since, either all the balls can be blue or black but not red)
P(E) = \(\frac{5}{84}\)

Question 3.
A card is drawn from a well shuffled pack of 52 cards. Let E, “a king or a queen is drawn” & E₂: “a queen or a jack is drawn”, then:
(a) E₁ and E₂ are not independent
(b) E₁ and E₂ are mutually exclusive
(c) E₁ and E₂ are independent
(d) None of these [1 Mark, Nov. 2006]
Solution:
(a) E₁ and E₂ are not independent
Note only one experiment made, so, they are not Independent.
Detail:- E₁ = a king or a queen is drawn
E₂ = a queen or a jack is drawn
P(E₁) = \(\frac{4+4}{52}\) = \(\frac{8}{52}\)
P(E₂) = \(\frac{4+4}{52}\) = \(\frac{8}{52}\)
P(E₁ ∩ E₂) = p (drawing a queen) = \(\frac{4}{52}\)
Here P(E₁ ∩ E₂) ≠ P(E₁).P(E₂)
Hence E₁ and E₂ are not independent

Question 4.
In a non-leap year, the probability of getting 53 Sundays or 53 Tuesdays or 53 Thursdays is : [1 Mark, Feb. 2007]
(a) \(\frac{4}{7}\)
(b) \(\frac{2}{7}\)
(c) \(\frac{3}{7}\)
(d) \(\frac{1}{7}\)
Solution:
(c) \(\frac{3}{7}\)

1 non – leap year = 365 days,
= 52 complete weeks and 1 additional day
S = (Sun.; Mon.; Tue.; Wed.; Thur.; Fri.;Sat.}; n (S) = 7
Required Event = E = {Sun.,Tue.,Thur.}
n (E) = 3
P(E) = \(\frac{3}{7}\)

Question 5.
If A andB are two events and P(A) = \(\frac{3}{8}\), P(B) = \(\frac{1}{2}\), P(A∩B) = \(\frac{1}{4}\), then the value of P(A’ ∪ B’) is [1 Mark, Feb. 2007]
(a) \(\frac{1}{4}\)
(b) \(\frac{3}{4}\)
(c) \(\frac{5}{8}\)
(d) \(\frac{5}{4}\)
Solution:
(b) \(\frac{3}{4}\)
P(A ∩ B) = \(\frac{1}{4}\)
According to De-Morgans Law
P(A’ ∪ B’) = P(A∩B)’
= 1 – P(A∩B) = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)

Question 6.
From a pack of cards, two are drawn, the first being replaced before the second is drawn. The chance that the first is a diamond and the second is king is: [May 2007]
(a) \(\frac{1}{52}\)
(b) \(\frac{3}{2704}\)
(c) \(\frac{4}{13}\)
(d) \(\frac{3}{52}\)
Solution:
(a) \(\frac{1}{52}\)
Required probability
= P(card drawn is a diamond) × P (card drawn is a king)
= \(\frac{13}{52}\) × \(\frac{4}{52}\)(since there are 13 diamonds and 4 kings).
= \(\frac{1}{52}\)

Question 7.
The theory of compound probability states that for any two events A and B:
(a) P (A ∩ B) = P(A) × P(B)
(b) P (A ∩ B) = P(A) × P(B/A)
(c) P (A ∪ B) = P(A) × P(B/A)
(d) P (A ∪ B) = P(A) + P(B) – P(A ∩ B) [1 Mark, May 2007]
Solution:
(b) P (A ∩ B) = P(A) × P(B/A)
Simultaneous Occurrence of two events A and B are Compound Events
For it; Formula
P(A∩B) = P(A) × P(B/A)

Question 8.
The probability of getting qualified in IIT – JEE and AIEEE by a student are respectively \(\frac{1}{5}\) and \(\frac{3}{5}\). The probability that the student gets qualified for one of the these tests is :
[1 Mark, May 2007]
Solution:
(a) \(\frac{17}{25}\)
(b) \(\frac{22}{25}\)
(c) \(\frac{8}{25}\)
(d) \(\frac{3}{25}\)
Solution:
(a) The Events for being selected for IIT JEE & AIEEE are E₁ & E₂ respectively.
So, P(E₁) = \(\frac{1}{5}\); P(E₂) = \(\frac{3}{5}\)
The probability that he is selected for one of these test = 1 – P (selection in no tests)
= 1 – P(E₁‘)P(E₂‘)
= 1 – (1 – \(\frac{1}{5}\)) × (1 – \(\frac{3}{5}\)) = \(\frac{17}{25}\)

Question 9.
Suppose E and F are two events of a random experiment. If the probability of occurrence of E is \(\frac{1}{5}\) and the probability of occurrence of F given E is \(\frac{1}{10}\), then the probability of non-occurrence of at least one of the events E and F is : [1 Mark, Aug. 2007]
(a) \(\frac{1}{50}\)
(b) \(\frac{1}{25}\)
(c) \(\frac{13}{50}\)
(d) \(\frac{49}{50}\)
Solution:
(d) \(\frac{49}{50}\)
Given P(E) = \(\frac{1}{5}\), P(F/E) = \(\frac{1}{10}\)
∴ P(E ∩ F) = P(E).P(F/E)
= \(\frac{1}{5}\).\(\frac{1}{10}\) = \(\frac{1}{50}\)
∴ P(non-occurrence of at least one of the events of E and F)
P(E’∪F’) = P(E∩F)’
= 1 – P(E ∩ F)
= 1 – \(\frac{1}{50}\) = \(\frac{49}{50}\)

Question 10.
A bag contains 8 red and 5 white balls. Two successive draws of 3 balls are made without replacement. The probability that the first draw will produce 3 white balls and second 3 red balls is : [1 Mark, Aug. 2007]
(a) \(\frac{6}{255}\)
(b) \(\frac{5}{548}\)
(c) \(\frac{7}{429}\)
(d) \(\frac{3}{233}\)
Solution:
(c) \(\frac{7}{429}\)
P(1st 3 white then 3 red balls)
= P (White). P (Red) =
\(\frac{5 C_3}{13 C_3}\) . \(\frac{8 C_3}{10 C_3}\) = \(\frac{10}{286}\) × \(\frac{56}{120}\) = \(\frac{5}{143}\) × \(\frac{7}{15}\) = \(\frac{7}{429}\)

Question 11.
Three identical dice are rolled. The probability that the same number will appear on each of them is: [1 Mark, Feb. 2007]
(a) 1/6
(b) 1/12
(c) 1/36
(d) 1
Solution:
(c) 1/36
n (S) = 6³ = 216
Event A = same number appears on each of the three dice.
= {(1, 1, 1) ; (2, 2, 2) ; (3, 3, 3) ; (4, 4, 4) ; (5, 5, 5) ; (6, 6, 6)}
So, n(A) = 6
P(E) = \(\frac{6}{6 \times 6 \times 6}\) = \(\frac{1}{36}\)

Question 12.
Among the examinees in an examination 30%, 35% and 45% failed in Statistics, in Mathematics and in at least one of the subjects respectively. An examinee is selected at random. Find the probability that he failed in Mathematics only: [1 Mark, Nov. 2007]
(a) 0.245
(b) 0.25
(c) 0.254
(d) 0.55
Solution:
(a) 0.245
Event S = Students failed in Statistics, and
Event M = students failed in Mathematics
P(S) = 0.30,
P(M) = 0.35
and ∴ P(S ∪ M) = 0.45
Hence P(failed in mathematics) = P (failed in Mathematics but passed in Statistic)
= P(M) × P(S’)
= 0.35 × (1 – 0.30) = 0.245

Question 13.
An article consists of two parts A and B. The manufacturing process of each part is such that probability of defect in A is 0.08 and that in B is 0.05. What is the probability that the assembled product will not have any defect? [1 Mark, Feb. 2007]
(a) 0.934
(b) 0.864
(c) 0.85
(d) 0.874
Solution:
(d) 0.874

Let X = Event (Part A is non-defective) and Y = Event (Part B is non-defective)
∴ P(X) = 1 – 0.08 = 0.92
P(Y) = 1 – 0.05 = 0.95
P(Products are non-defective) = P(X ∩ Y) = P(X).P(Y) = 0.92 × 0.95 = 0.874

Question 14.
If 10 men, among whom are A and B, stand in a row, what is the probability that there will be exactly 3 men between A and B ? [1 Mark, Feb. 2008]
(a) 11/15
(b) 4/15
(c) 1/15
(d) 2/15
Solution:
(d) 2/15
There are 2 men standing in a row.
A and B are 2 men can take any 2 positions out of 10 in ¹⁰C₂ = 45 ways.
So, n(S) = 45.(2!) = 45 × 2 = 90. (∵ A and B can interchange their positions)
According to the Qts.
E = Event of placing 3 men between A & B = {(1, 5) ;(2, 6);(3, 7);(4, 8); (5, 9); (6 ,10); (5, 1), (6, 2), ; (10, 6)}
n(E) = 6.(2!) = 6 × 2 = 12
P(E) = \(\frac{n(E)}{n(S)}\) = \(\frac{6 \times 2}{45 \times}\) = \(\frac{2}{15}\)

Question 15.
The probability of an event can assume any value between: [1 Mark, Feb. 2008]
(a) 0 and 1
(b) -1 and 0
(c) -1 and 1
(d) None of these
Solution:
(d) None of these
Since the Probability of an event lies between 0 and 1, both inclusive i.e. 0 ≤ P(A) ≤ 1.

Question 16.
The odds are 9 : 5 against a person who is 50 years living till he is 70 and 8 : 6 against a person who is 60 living till he is 80. Find the probability that at least one of them will be alive after 20 years: [1 Mark, Feb. 2008]
(A) \(\frac{11}{14}\)
(B) \(\frac{22}{49}\)
(C) \(\frac{31}{49}\)
(D) \(\frac{35}{49}\)
Solution:
(C) \(\frac{31}{49}\)
Event A : Person aged 50 years will remain alive for next 20 years
Event B: Person aged 60 years will remain alive next 20 years
Given: \(\frac{\mathrm{P}\left(\mathrm{A}^{\prime}\right)}{\mathrm{P}(\mathrm{A})}\) = \(\frac{9}{5}\) & \(\frac{\mathrm{P}\left(\mathrm{B}^{\prime}\right)}{\mathrm{P}(\mathrm{B})}\) = \(\frac{8}{6}\)
∴ P(A’) = \(\frac{9}{9+5}\) = \(\frac{9}{14}\) & P(B’) = \(\frac{8}{8+6}\) = \(\frac{8}{14}\)
P (Atleast one will remain alive) = 1 – P (None will remain alive)
= 1 – P(A’).P(B’) = 1 – \(\frac{9}{14}\).\(\frac{8}{14}\) = \(\frac{124}{196}\) = \(\frac{31}{49}\)

Question 17.
If P(A) = P and P (B) = q, then:
(a) P (A/B) ≤ q/p
(b) P(A/B) ≥ p/q
(c) P(A/B) ≤ p/q
(d) P(A/B) ≥ q/p [1 Mark, Feb. 2008]
Solution:
(c) P(A/B) ≤ p/q
Given P(A) = P and P(B) = q
We know that
P(A/B) = \(\frac{P(A \cap B)}{P(B)}\)
and also
P(A ∩ B) < P(A)
Dividing by P(B) on both sides ; We get
\(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}\) ≤ \(\frac{P(A)}{P(B)}\)
∴ P(A/B) ≤ p/q

Question 18.
The probability that a trainee will remain with a company is 0.8. The probability that an employee earns more than ₹ 20,000 per month is 0.4. The probability that an employee, who was a trainee and remained with the company or who earns more than ₹ : 20,000 per month is 0.9. What is the probability that an employee earns more than ₹ 20,000 per month given that he is a trainee, who stayed with the company ? [1 Mark, June 2018]
Solution:
(a) 5/8
(b) 3/8
(c) 1/8
(d) 7/8
Solution:
(b) 3/8

Let Event A = A trainee will remain with the company & Event B = An Employee earns more than ₹ 20,000.
Given P(A) = 0.8, P(B) = 0.4 and P(A ∪ B) = 0.9
∴ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
⇒ 0.9 = 0.8 + 0.4 – P(A ∩ B)
⇒ P(A ∩ B) = 0.3
Hence P(B/A) = \(\frac{P(B \cap A)}{P(A)}\) = \(\frac{0.3}{0.8}\) = \(\frac{3}{8}\)

Question 19.
The limiting relative frequency of probability is: [1 Mark, Dec. 2008]
(a) Axiomatic
(b) classical
(c) statistical
(d) Mathematical
Solution:
(c) statistical

The limitations of the statistical definition of probability, based on the concept of relative frequency:—
Let an event A occurs A times. Then, the limiting value of the ratio of f_A to n as n tends to infinity is defined as the probability of A.

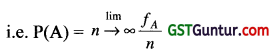
Therefore, the limiting relative frequency of probability is Statistical.

Question 20.
If A and B are two independent events and P (A ∪ B) = 2/5; P(B) = 1/3 Find P(A)
(a) 2/9
(b) -1/3
(c) 2/10
(d) 1/10 [1 Mark, June 2009]
Solution:
(d) 1/10
Since A and B are two independent events, therefore –
P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
⇒ P(A). P(B) = P(A) + P(B) – P(A ∪ B)
⇒ P(A)(\(\frac{1}{3}\) – 1) = \(\frac{5-6}{15}\)
⇒ P(A).\(\left(\frac{-2}{3}\right)\) = \(-\frac{1}{15}\)
∴ P(A) = \(\frac{1}{10}\)

Question 21.
A bag contains 12 balls of which 3 are red 5 balls are drawn at random Find the probability that in 5 balls 3 are red. [1 Mark, June 2009]
(a) 3/132
(b) 5/396
(c) 1/36
(d) 1/22
Solution:
(d) 1/22
Sample Space n (S) = ¹²C₅
No. of Red balls = 3 ;
Other colour balls = 9;
n (E) = Event of 3 red balls if 5 balls are drawn. = ³C₃ . ⁹C₂
P(E) = \(\frac{{ }^3 C_3 \times{ }^9 C_2}{{ }^{12} C_5}\) = \(\frac{1 \times 36}{792}\) = \(\frac{1}{22}\)

Question 22.
P(A) = 2/3; P(B) = 3/5; P(A∪B) = 5/6. Find P(B/A)
(a) 11/20
(b) 13/20
(c) 13/18
Solution:
(b) 13/20
∵ P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= \(\frac{2}{3}\) + \(\frac{3}{5}\) – \(\frac{5}{6}\)
= \(\frac{20+18-25}{30}\) = \(\frac{13}{30}\)

Question 23.
If P (A ∩ B) = P (A) × P (B), then the events are:
(a) Independent events
(b) Mutually exclusive events
(c) Exhaustive events
(d) Mutually inclusive events
Solution:
(a) Independent events
If A and B are two independent events, then P(A ∩ B) = P(A) × P(B).

Question 24.
In a pack of playing cards with two jokers probability of getting king of spade is
(a) 4/13
(b) 4/52
(c) 1/52
(d) 1/54
Solution:
(d) 1/54

Total No. of playing cards = 52 + 2 = 54
sample space n(S) = ⁵⁴C₁ = 54
Total no. of spade king = 1
E = Event of getting 1 spade king = 1
∴ P(E) = \(\frac{1}{54}\)

Question 25.
Consider two events A and B not mutually exclusive, such that P(A) = 1/4, P(B) = 2/5, P(A ∪ B) = 1/2, then P(A\(\overline{\mathrm{B}}\)) is [1 Mark, June 2010]
(a) 3/7
(b) 2/10
(c) 1/10
(d) None of them
Solution:
(d) None of them
Since events A & B are not mutually exclusive. So, they are independent events.
P(AB) = P(A ∩ B) = P(A) .P(B)
∴ P(A \(\overline{\mathrm{B}}\)) = P(A) – P(A ∩ B) = P(A) – P(A).P(B)
= P(A).[1 – (B)]
= \(\frac{1}{4}\).(1 – \(\frac{2}{5}\)) = \(\frac{1}{4}\) . \(\frac{3}{5}\) = \(\frac{3}{20}\)

Question 26.
If x be the sum of two numbers obtained when two dice are thrown simultaneously then P(x ≥ 7) is
(a) 5/12
(b) 7/12
(c) 11/15
(d) 3/8
Solution:
(b) 7/12
Sample Space n (S) = 36
E = Event of getting X > = 7
= {(1, 6) ; (2, 5) ; (3, 4) ; (4 ; 3) ; (5, 2) ; (6, 1); (2, 6) ; (3, 5) ; (4, 4) ; (5, 3) ; (6, 2); ………;(6,6)}; ∴ n(E) = 21
∴ Required Probability P(E) = \(\frac{21}{36}\) = \(\frac{7}{12}\)
Tricks See Nov. 2019 Qts.

Question 27.
If P(A/B) = P(A), then A and B are
(a) Mutually exclusive events
(b) Dependent events
(c) Independent events
(d) Composite events [1 Mark, Dec. 2010]
Solution:
(c) Independent events
P(A/B) = P(A)
Hence, A and B are independent events.

Question 28.
A bag contains 3 white and 5 black balls and second bag contains 4 white and 2 black balls. If one ball is taken from each bag, the probability that both the balls are white is _____ [1 Mark, Dec. 2010]
(a) 1/3
(b) 1/4
(c) 1/2
(d) None of these
Solution:
(b) 1/4

Let A = Event of getting 1 white ball from 1st bag.
B = Event of getting 1 white ball from 2nd bag.
A & B are Independent Events.
P(A ∩ B) = P(A).P(B)
\(\frac{{ }^3 \mathrm{C}_1}{{ }^8 \mathrm{C}_1} \cdot \frac{{ }^4 \mathrm{C}_1}{{ }^6 \mathrm{C}_1}\) = \(\frac{3}{8} \times \frac{4}{6}\) = \(\frac{1}{4}\)

Question 29.
The odds in favour of A solving a problem is 5:7 and Odds against B solving the same problem is 9:6. What is the probability that if both of them try, the problem will be solved?
(a) 117/180
(b) 181/200
(c) 147/180
(d) 119/180 [1 Mark, Dec. 2010]
Solution:
(a) 117/180

P(A) = \(\frac{5}{12}\) ; P(B) = \(\frac{6}{15}\)
Probability that problem will be Solved = 1 – Prob. that problem not solved
= 1 – P(A’).P(B’)
= 1 – [1 – P(A)][1 – P(B)]
= 1 – (1 – \(\frac{5}{12}\))(1 – \(\frac{6}{15}\))
= 1 – \(\frac{7}{12}\) × \(\frac{9}{15}\) = \(\frac{180-63}{180}\) = \(\frac{117}{180}\)

Question 30.
Consider Urn 1:2 white balls, 3 black balls; Urn II: 4 white balls, 6 black balls. One ball is randomly transferred from first to second Urn, then one ball is drawn from II Urn. The probability that drawn ball is white is
(a) 22/65
(b) 22/46
(c) 22/55
(d) 21/45 [1 Mark, Dec. 2010]
Solution:
(c) 22/55

Case I: 1 Black ball is transferred from Urn I to Urn II and then a white ball is picked from Urn II
Prob. = \(\frac{3}{5}\) × \(\frac{4}{11}\) = \(\frac{12}{55}\)
Case II: 1 White ball is transferred from Urn I to II and then a white ball is picked from Urn II
Prob. = \(\frac{2}{5}\) × \(\frac{5}{11}\) = \(\frac{10}{55}\)
From Case I + Case II;
P(Whiteball) = \(\frac{12}{55}\) + \(\frac{10}{55}\) = \(\frac{22}{55}\)

Question 31.
If P (A∪B)= P(A), Find P(A∩B).
(a) P(A).P(B)
(b) P(A) + P(B)
(c) 0
(d) P(B) [1 Mark, June 2011]
Solution:
(d) P(B)
Given : P(A ∪ B) = P(A) we know that
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
∴ we get P(A ∩ B) = P(B)

Question 32.
A bag contains 5 Red balls, 4 Blue Balls and ‘m’ Green Balls. If the random probability of picking two green balls is 1/7. What is the No. of green Balls (m)
(a) 5
(b) 7
(c) 6
(d) None of above [1 Mark, June 2011]
Solution:
(c) 6
Total balls = 5 + 4 + m = m + 9
∴ Probability of picking two green balls = \(\frac{1}{7}\)

TRICKS : Go by choices
For (c) Total = 6 + 9 = 15
P = \(\frac{{ }^6 c_2}{{ }^{15} c_2}\)
= \(\frac{15}{105}\) = \(\frac{1}{7}\) (True)

Question 33.
The probability of Girl getting scholarship is 0.6 and the same probability for Boy is 0.8 Find the probability that at least one of the categories getting scholarship. [1 Mark, June 2011]
(a) 0.32
(b) 0.44
(c) 0.92
(d) None of these
Solution:
(c) 0.92

Given
Probability of Girl getting scholarship P(A) = 0.6
Probability of Boy getting scholarship P(B) = 0.8
Required of at least one category getting scholarship:
= 1 – P(None getting scholarship)
= 1 – P (A’) .P(B’) = 1 – (1 – 0.6).( 1 – 0.8)
= 1 – (0.4). (0.2) = 1 – 0.08 = 0.92

Question 34.
A coin is tossed 5 times, what is the probability that exactly 3 heads will occur.
(a) \(\frac{5}{16}\)
(b) \(\frac{1}{32}\)
(c) \(\frac{5}{36}\)
(d) \(\frac{3}{32}\)
Solution:
(a) \(\frac{5}{16}\)

(a) Total No. of Tails (n) = 5
r = 3
Probability of getting Head (p) = 1/2
Probability of getting Tail (q) = 1/2
By Binomial Distribution,
P(x = r) = ⁿC_rp^rq^n-r
P(r = 3) = ⁵C₃\(\left(\frac{1}{2}\right)^3\left(\frac{1}{2}\right)^{5-3}\) = 10.\(\frac{1}{2^5}\) = \(\frac{10}{32}\) = \(\frac{5}{16}\)

Question 35.
Arun & Tarun appear for an interview for two vacancies. The probability of Arun’s selection is 1/3 and that of Tarun’s selection is 1/5. Find the probability that only one of them will be selected.
(a) 2/5
(b) 4/5
(c) 6/5
(d) 8/5
Solution:
(a) 2/5

Let A & T are events of selection of Aran and Taran respectively.
P(A) = \(\frac{1}{3}\)
∴ \(\mathrm{P}(\bar{A})\) = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
P(T) = \(\frac{1}{5}\)
∴ P(\(\bar{T}\)) = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
∴ Probability that only one will be selected = P(A). P(\(\bar{T}\)) + P(\(\bar{A}\)).P(T)
= \(\frac{1}{3}\) × \(\frac{4}{5}\) + \(\frac{2}{3}\) × \(\frac{1}{5}\) = \(\frac{4}{15}\) + \(\frac{2}{15}\) = \(\frac{6}{15}\) = \(\frac{2}{5}\)

Question 36.
A company employed 7 CA’s, 6 MBA’s and 3 Engineer’s. Inhowmany ways the company can form a committee if the committee has two members of each type.
(a) 900
(b) 1,000
(c) 787
(d) 945 [1 Mark, June 2012]
Solution:
(d) 945
The number of ways to make a committee containing two members of each type
= ⁷C₂ × ⁶C₂ × ³C₂
= 21 × 15 × 3
= 945

Question 37.
Two dice are thrown together. Find the probability of getting a multiple of 2 on one dice and multiple of 3 on the other. [1 Mark, Dec. 2012]
(a) 2/3
(b) 1/6
(c) 1/3
(d) None of the above
Solution:
(b) 1/6
Sample space n(S) = 36
Let ‘E’ = ‘Events of getting a multiple of 2 on the 1st die and multiple of 3 on the IInd die
= {(2, 3) ; (2, 6) ; (4, 3) ; (4, 6) ; (6, 3) ; (6, 6)}
n(E) = 6
P(E) = \(\frac{n(E)}{n(S)}\) = \(\frac{6}{36}\) = \(\frac{1}{6}\)

Question 38.
The odds against A solving a certain problem are 4 to 3 and the odds in favour of B solving the same problem are 7 to 5 .What is the probability that the problem will be solved if they both try?
(a) 15/21
(b) 16/21
(c) 17/21
(d) 13/21 [1 Mark, Dec. 2012]
Solution:
(b) 16/21

The odd against A solving a certain problem = 4 : 3
P(A) = Prob (to solve the problem) = \(\frac{3}{4+3}\) = \(\frac{3}{7}\)
P(\(\bar{A}\)) = prob (not to solve the problem) = \(\frac{4}{4+3}\) = \(\frac{4}{7}\)
The odds in favour of B solving the same problem = 7 : 5
P(B) = Prob (to solve the problem) = \(\frac{7}{7+5}\) = \(\frac{7}{12}\)
P(\(\bar{B}\)) = Prob (not to solve the problem) = \(\frac{5}{7+5}\) = \(\frac{5}{12}\)
Probability (the problem is solved)
1 – \(P(\bar{A} \cap \bar{B})\) = 1 – \(\mathrm{P}(\overline{\mathrm{A}}) \cdot \mathrm{P}(\overline{\mathrm{B}})\) = 1 – \(\frac{4}{7} \cdot \frac{5}{12}\)
Probability (problem is solved) = 1 – \(\frac{5}{21}\) = \(\frac{16}{21}\)

Question 39.
A bag contains 6 red balls and some blue balls. If the probability of drawing a blue ball from the bag is twice that of a red ball, find the number of blue balls in the bag (1 Mark, Dec. 2012)
(a) 10
(b) 12
(c) 14
(d) 16
Solution:
(b) 12

Let No. of Blue ball, = X
Total Ball in the Bag = (6 + X)
Prob of a Red ball P(R) = \(\frac{{ }^6 \mathrm{C}_1}{{ }^{6+x} \mathrm{C}_1}\) = \(\frac{6}{6+x}\)
and prob of a Blue Ball P(B) = \(\frac{{ }^x C_1}{{ }^{6+x} C_1}\) = \(\frac{x}{6+x}\)
Given, P(B) = 2P(R)
\(\frac{X}{(6+X)}\) = \(\frac{2 \times 6}{(6+X)}\) ⇒ X = 12
Tricks : GBC

Question 40.
The odds that a book will be received favourably by 3 independent reviewers are 5 to 2, 3 to 4, 4 to 3 respectively, then the probability that out of 3 critics the majority will be favorable is ______ [1 Mark, June 2013]
(a) \(\frac{209}{343}\)
(b) \(\frac{209}{434}\)
(c) \(\frac{209}{443}\)
(d) \(\frac{209}{350}\)
Solution:
(a) \(\frac{209}{343}\)
(a) is correct
Let A; B and C are three independent reviewers (Event)
Given: odds in favour of Events

Prob.(Majority will be favourable) =
P( A).P(B).P(C’) + P(A)P(B’)P(C) + P(A’).P(B).P(C) + P(A).P(B).P(C)
= \(\frac{5}{7}\).\(\frac{5}{7}\).\(\frac{3}{7}\).+\(\frac{5}{7}\).\(\frac{4}{7}\).\(\frac{4}{7}\). + \(\frac{2}{7}\).\(\frac{3}{7}\).\(\frac{4}{7}\) + \(\frac{5}{7}\).\(\frac{3}{7}\).\(\frac{4}{7}\).
= \(\frac{45+80+24+60}{343}\) = \(\frac{209}{343}\)

Question 41.
Find the probability of drawing spade on each of 2 consecutive draws from a well shuffled pack of cards when the draws are without replacement. [1 Mark, June 2013]
(a) \(\frac{2}{51}\)
(b) \(\frac{3}{51}\)
(c) \(\frac{4}{51}\)
(d) \(\frac{4}{51}\)
Solution:
(b) \(\frac{3}{51}\)
(b) is correct
P(spades on consecutive draws of 2 cards)
= \(\frac{13}{52_{c_1}} \times \frac{12_{c_1}}{51_{c_1}}\) = \(\frac{13}{52} \times \frac{12}{51}\)
= \(\frac{3}{51}\) = \(\frac{1}{17}\)

Question 42.
A bag contains 2 red 3 green and 2 blue balls. If 2 balls are drawn at random from the bag find the probability that none of them will be blue.
(a) \(\frac{11}{21}\)
(b) \(\frac{5}{7}\)
(c) \(\frac{10}{21}\)
(d) \(\frac{2}{7}\) [1 Mark, June 2013]
Solution:
(c) \(\frac{10}{21}\)
(c) is correct
Sample Space = n ( S ) = ⁷C₂ = 21
p(None are blue) = \(\frac{5_{c_2}}{7_{c_2}}\) = \(\frac{10}{21}\)

Question 43.
If P(A) = 0.45, P(B) = 0.35, P(A and B) = 0.25 then P(A/B)
(a) 1.4
(b) 1.8
(c) 0.714
(d) 0.556 [1 Mark, Dec. 2013]
Solution:
(c) 0.714
(c) is correct
P(A/B) = \(\frac{P(A \cap B)}{P(B)}\) = \(\frac{0.25}{0.35}\)
= 0.714

Question 44.
Two coins are tossed simultaneously then the probability of getting exactly one head is [1 Mark, Dec. 2013J
(a) \(\frac{3}{4}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{1}{4}\)
(d) \(\frac{1}{2}\)
Solution:
(d) \(\frac{1}{2}\)
(d) is correct
P(Exactly 1 head) = P(H).P(T) + P(T).P(H)
= \(\frac{1}{2}\).\(\frac{1}{2}\) + \(\frac{1}{2}\).\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\)

Question 45.
The probability that a cricket team winning a match at Kanpur is 2/5 and loosing a match at Delhi is 1/7 .What is the probability of the team winning at least one match ? [1 Mark, Dec. 2013]
(a) \(\frac{3}{35}\)
(b) \(\frac{32}{35}\)
(c) \(\frac{18}{35}\)
(d) \(\frac{17}{35}\)
Solution:
(b) \(\frac{32}{35}\)
P(At least 1 match win) = 1 – P (No match win)
= 1 – (1 – \(\frac{2}{5}\))\(\frac{1}{7}\) = 1 – P (Loosing at Kanpur).P (Loosing at Delhi)
= 1 – \(\frac{3}{5}\).\(\frac{1}{7}\) = 1 – \(\frac{3}{35}\) = \(\frac{32}{35}\)

Question 46.
For any two events
A₁, A₂; let P(A₁) = \(\frac{2}{3}\), P(A₂) = \(\frac{3}{8}\), P(A₁ ∩ A₂) = \(\frac{1}{4}\) then A₁, A₂ are
(a) Mutually Exclusive but not independent events
(b) Mutually Exclusive and iñdependent events
(c) Independent but not Mutually Exclusive
(d) None [1 Mark, June 2014]
Solution:
(c) Independent but not Mutually Exclusive
(c) is correct
(A₁ ∩ A₂) = \(\frac{1}{4}\) ≠ 0
So, A₁ and A₂ are not Mutually Exclusive Events.
P(A₁ ∩ A₂) = P(A₁).P(A₂)
= \(\frac{2}{3}\) × \(\frac{3}{8}\) = \(\frac{1}{4}\) (given)
∴ A₁ & A₂ are clearly Independent Events

Question 47.
If a pair of dice is thrown what is the probability of occurring neither 7 nor 11 ?
(a) \(\frac{1}{6}\)
(b) \(\frac{1}{8}\)
(c) \(\frac{2}{9}\)
(d) \(\frac{7}{9}\) [1 Mark, June 2014]
Solution:
(d) \(\frac{7}{9}\)
(d) is correct
n(s) = 6² = 36
Let A Event of getting Their sum = 7
= {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
n(A) = 6
Let B = Event of getting their sum = 11
= {(5, 6) ; (6, 5)}
n(B) = 2
P(A ∪ B) = \(\frac{n(A)+n(B)}{n(s)}\)
[∵ A & B are mutually Exclusive Events]
= \(\frac{6+2}{36}\) = \(\frac{8}{36}\) = \(\frac{2}{9}\)
P(Neither 7 nor 11) = P(A ∪ B)’
= 1 – p(A ∪ B)
= 1 – \(\frac{2}{9}\) = \(\frac{7}{9}\)

Question 48.
An urn contains 2 red and 1 green balls, another urn contains 2 red and 2 green balls. An urn was selected at random and then a ball was drawn from it. ¡fit was found to be red then the probability that it has been drawn from first urn is
(a) \(\frac{4}{7}\)
(b) \(\frac{3}{7}\)
(c) \(\frac{2}{3}\)
(d) \(\frac{7}{12}\) [1 Mark, June 2014]
Solution:
(a) \(\frac{4}{7}\)
(a) is correct

Baye’s Theorem Question
Let A & B are selection of 1^st & 2^nd urns respectively.
∴ P(A) = P(B) = \(\frac{1}{2}\)
E = Event of getting red ball.
P(E/A) = \(\frac{2}{3}\); P(E/B) = \(\frac{2}{4}\) = \(\frac{1}{2}\)

Question 49.
If 6 coins are tossed simultaneously then the probability of obtaining exactly 2 heads is
(a) \(\frac{1}{64}\)
(b) \(\frac{63}{64}\)
(c) \(\frac{15}{64}\)
(d) None [1 Mark, Dec. 2014]
Solution:
(c) \(\frac{15}{64}\)
(c) is correct
n = 6; p = \(\frac{1}{2}\)(prob. of getting head)
q = 1- p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
p(x = 2) = ⁶C2.p².q⁴ = 15.\(\left(\frac{1}{2}\right)^2 \cdot\left(\frac{1}{2}\right)^4\) = \(\frac{15}{64}\)

Question 50.
A die is thrown twice then the probability that the sum of the number is divisible by 4 is
(a) \(\frac{1}{9}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{11}{36}\)
(d) \(\frac{1}{4}\) [1 Mark, Dec. 2014]
Solution:
(d) \(\frac{1}{4}\) [1 Mark, Dec. 2014]
(d) is correct
n(s) = 6² = 36
Let E = Event that the sum of numbers is divisible by 4.
= {(1, 3), (2, 2), (3, 1), (2, 6), (3, 5), (4, 4), (5, 3), (6, 2), (6, 6)}
n(E) = 9
∴ P(E) = \(\frac{n(E)}{n(S)}\) = \(\frac{9}{36}\) = \(\frac{1}{4}\)

Question 51.
There are 6 positive and 8 negative numbers. Four number are selected at random without replacement and multiplied. Find the probability that the product is positive. [1 Mark, June 2015]
(a) \(\frac{420}{1001}\)
(b) \(\frac{409}{1001}\)
(c) \(\frac{70}{1001}\)
(d) \(\frac{505}{1001}\)
Solution:
(d) \(\frac{505}{1001}\)
(d) is correct
Let 6 positive Nos. are 1,2, 3,4, 5, 6,
and 8 negative Nos. are -1,-2,-3, ……..; -8
∴ Sample space
= n(s) = ¹⁴C4 = \(=\frac{14 !}{(4 !)(10 !)}\)
= \(\frac{14 \cdot 13 \cdot 12.11 .10 !}{4 \cdot 3 \cdot 2 \cdot 1.10 !}\)
= 1001
Let Event = E = such that product of them is positive
n(E) = ⁶C₄ + ⁶C₂, ⁸C₂ + ⁸C₄ = (All + ve) (Two +ve & two -ve) + (All 4 are -ve)
= 15 + 15 × 28 + 70
= 505
∴ P(E) = \(\frac{n(E)}{n(S)}\) = \(\frac{505}{1001}\)

Question 52.
P(A₁) = 3 /8; P(A₂) = 2 /3; P(A₁ ∩ A₂) = 1/4 then A₁ and A₂ will be
(a) Mutually exclusive & independent
(b) Exclusive but not independent
(c) Independent but not exclusive
(d) None [1 Mark, June 2015]
Solution:
(c) Independent but not exclusive
(c) is correct
∵ P(A₁ ∩ A₂) = \(\frac{1}{4}\) (given) ≠ 0
∴ A₁ & A₂ are not Mutually Exclusive Events
P(A₂ ∩ A₂) = P(A₁).P(A₂) = \(\frac{3}{8} \times \frac{2}{3}\) = \(\frac{1}{4}\)
Clearly A₁ and A₂ are Independent Events

Question 53.
The sum of two numbers obtained in a single throw of two dice is ‘ S ’ .Then the probability of ‘s’ will be maximum when ‘S’ = [1 Mark, June 2015]
(a) 5
(b) 7
(c) 6
(d) 8
Solution:
(b) 7
(b) is correct
S = Sum of face values of two due.
S = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
n(s) = 6 it is maximum if sum of their face is 7.

Question 54.
When an unbiased dice is rolled, find the odds in favour of getting of multiple of 3.
(a) 1/6
(b) 1/4
(c) 1/2
(d) 1/3 [1 Mark, Dec. 2015]
Solution:
(c) 1/2
(c) is correct S = {1, 2, 3, 4, 5, 6}
Let E = {3, 6}; E’ = {1, 2, 3, 4, 5, 6} – {3, 6}
= {1, 2, 4, 5} ⇒ n(E) = 2; n(E’) = 4
Odds in favour of Event E = \(\frac{n(\mathrm{E})}{n\left(\mathrm{E}^1\right)}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\)

Question 55.
Three coins are rolled, what is the probability of getting exactly two heads:
(a) 1/8
(b) 3/8
(c) 7/8
(d) 5/8 [1 Mark, Dec. 2015]
Solution:
(b) 3/8
(b) is correct.
Given n = 3
P = Prob. (head) in 1 trial = \(\frac{1}{2}\)
q = 1 – p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
P(X = 2) = ³C₂.p².q¹ = 3.\(\left(\frac{1}{2}\right)^2 \cdot \frac{1}{2}\) = \(\frac{3}{8}\)

Question 56.
If a random sample of 500 Oranges produces 25 rotten oranges. Then the estimate of the proportion of rotten oranges in the sample is : [1 Mark, Dec. 2015]
(a) 0.01
(b) 0.05
(c) 0.028
(d) 0.0593
Solution:
(b) 0.05
(b) is correct.
P = \(\frac{25}{500}\) = 0.05

Question 57.
Two letter are drawn at random from word “ HOME” find the probability that there is no vowel.
(a) 5/6
(b) 1/6
(c) 1/3
(d) None [1 Mark, Dec. 2015]
Solution:
(b) 1/6
(b) is correct.
n(S) = ⁴C₂ = 6.
E = Event of no vowel = {H; M}
∴ n(E) = ²C₂ =1.
∴ P(E) = \(\frac{n(\mathrm{E})}{n(S)}\) = \(\frac{1}{6}\)

Question 58.
A bag contains 15 one rupee coins, 25 two rupee coins and 10 five rupee coins. If a coin is selected at random from the bag, then the probability of not selecting a one rupee coin is:
(a) 0.30
(b) 0.70
(c) 0.25
(d) 0.20 [1 Mark, Dec. 2015]
Solution:
(b) 0.70
(b) is correct.
P = \(\frac{25+10}{50}\) = 0.70

Question 59.
If P(A) = \(\frac{2}{3}\), P(B) = \(\frac{3}{5}\), P(A ∪ B) = \(\frac{5}{6}\), thenP(A/B’)is [1 Mark, June 2016]
(a) \(\frac{7}{12}\)
(b) \(\frac{5}{12}\)
(c) \(\frac{1}{4}\) (d)
(d) \(\frac{1}{2}\)
Solution:
(b) \(\frac{5}{12}\)

Question 60.
Two dice are tossed what is the probability that the total is divisible by 3 or 4
(a) \(\frac{20}{36}\)
(b) \(\frac{21}{36}\)
(c) \(\frac{14}{36}\)
(d) None [1 Mark, June 2016]
Solution:
(a) \(\frac{20}{36}\)
n(s)= 36
A = Event of getting Nos. such that the sum of their face Nos. is divisible by 3
= (sum 3 + sum 6 + sum 9 + sum 12)
= {(1, 2), (2, 1); (1, 5), (2, 4), (3, 3), (4, 2), (5, 1), (3, 6), (4, 5), (5, 4), (6, 3), (6, 6)}
n(A) = 12
B = Event of getting Nos. such that the sum of their face Nos. is divisible by 4 = (sum 4 + sum 8 + sum 12)
= {(1, 3), (2,2); (3, 1); (2, 6), (3, 5), (4, 4); (5, 3); (6, 2); (6, 6)}
n(B) = 9
A ∩ B = Divisible by LCM of 3 & 4 = 12 = sum 12 = {(6, 6)}
n (A ∩ B) = 1
P(A ∪ B) = \(\frac{n(\mathrm{~A})+n(\mathrm{~B})-n(\mathrm{~A} \cap \mathrm{B})}{n(\mathrm{~S})}\)
= \(\frac{12+9-1}{36}\) = \(\frac{20}{36}\) = \(\frac{5}{9}\)
(A) is correct.

Question 61.
If 2 dice are rolled simultaneously then the probability that their sum is neither 3 nor 6 is [1 Mark, June 2016]
(a) 0.5
(b) 0.75
(c) 0.25
(d) 0.80
Solution:
(d) 0.80

A = event that sum is 3 = {(1, 2); (2, 1)}
n (A)= 2
B = event that sum is 6
= {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
n (B) = 5
A ∩ B = ϕ

Question 62.
In a game, cards are thorughly shuffled and distributed equally among four players. What is the probability that a specific player gets all the four kings ? [1 Mark, June 2016]
(a) \(\frac{52_{c_4} \times 48_{c_{13}}}{52_{c_{11}}}\)
(b) \(\frac{4_{c_4} \times 48_{c_9}}{52_{c_{13}}}\)
(c) \(\frac{13_{c_9} \times 39_{c_9}}{52_{c_{13}}}\)
(d) \(\frac{4_{c_4} \times 39_{c_9}}{52_{c_{13}}}\)
Solution:
(b) \(\frac{4_{c_4} \times 48_{c_9}}{52_{c_{13}}}\)
Each candidate will get 13 cards.
∴ n(S) = ⁵²C₁₃
let E = Event of getting all 4 kings and rest 9 cards by a player out of 48.
∴ n(E) = ⁴C₄.⁴⁸C₉
∴ P(E) = \(\frac{n(\mathrm{E})}{n(\mathrm{~S})}\) = \(\frac{{ }^4 C_4{ }^{48} C_9}{{ }^{52} C_{13}}\)
(b) is correct

Question 63.
A bag contains 4 red and 5 black balls. Another bag contains 5 red, 3 black balls. If one ball is drawn at random from each bag. Then the probability that one red and one black ball drawn is _____.
(a) \(\frac{12}{72}\)
(b) \(\frac{25}{72}\)
(c) \(\frac{37}{72}\)
(d) \(\frac{13}{72}\) [1 Mark, June 2016]
Solution:
Prob. (1 red and 1 black balls)
= P(R₁).P(B₂) + P(B₁).P(R₂)
Where R₁ = event of getting red ball from 1^st bag.
R₂ = event of getting red ball from 2^nd bag.
B₁ = event of getting black ball from 1^st bag.
B₂ = event of getting black ball from 2^nd bag.
∴ Prob. = \(\frac{{ }^4 C_1}{{ }^9 C_1} \times \frac{{ }^3 C_1}{{ }^8 C_1}+\frac{{ }^5 C_1}{{ }^9 C_1} \times \frac{{ }^5 C_1}{{ }^8 C_1}\)
= \(\frac{4}{9} \times \frac{3}{8}+\frac{5}{9} \times \frac{5}{8}\) = \(\frac{12+25}{72}\) = \(\frac{37}{72}\)

Question 64.
In a discrete random variable follows uniform distribution and assumes only the value 8, 9, 11 , 15 , 18, 20. Then P(x ≤ 15) is
(a) 1/2
(b) 1/3
(c) 2/3
(d) 2/7
Solution:
(c) 2/3
E = Event of Nos. ≤ 15 = {8, 9, 11, 15}
P(X ≤ 15) = \(\frac{n(\mathrm{E})}{n(\mathrm{~S})}\) = \(\frac{4}{6}\) = \(\frac{2}{3}\)

Question 65.
A bag contains 6 green and 5 red balls. One ball is drawn at random. The probability of getting a red ball is?
(a) \(\frac{5}{11}\)
(b) \(\frac{6}{11}\)
(c) \(\frac{5}{6}\)
(d) None [1 Mark, Dec. 2016]
Solution:
(a) \(\frac{5}{11}\)
(a) is correct
n(S) = ¹¹C₁ = 11
Let E = Event of getting a red ball.
n (E) = ⁵C₁ = 5
P(E) = \(\frac{5}{11}\)

Question 66.
If two events A, B P(A)= \(\frac{1}{2}\); P(B) = \(\frac{1}{3}\) and P(A∪B) = \(\frac{2}{3}\), then find P(A ∩ B)?
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{6}\)
(c) \(\frac{2}{3}\)
(d) \(\frac{1}{2}\) [1 Mark, Dec. 2016]
Solution:
(b) \(\frac{1}{6}\)
(b) is correct.
P(A ∩ B) = P(A) + P(B) – P(A∪B)
= \(\frac{1}{2}\) + \(\frac{1}{3}\) – \(\frac{2}{3}\) = \(\frac{1}{6}\)

Question 67.
If P(A) = \(\frac{2}{3}\), P(B) = \(\frac{3}{8}\), (A ∩ B) = \(\frac{1}{4}\), then the even A & B are
(a) Independent and mutually exclusive
(b) Independent but not mutually exclusive
(c) Mutually exclusive but not independent
(d) Neither Independent nor exclusive [1 Mark, Dec. 2016]
Solution:
(b) Independent but not mutually exclusive
(b) is correct.
Since, P(A ∩ B) ≠ 0, S0 A & B are not mutually exclusive events.
Now, P(A ∩ B) = P(A). P(B) = \(\frac{2}{3}\).\(\frac{3}{8}\) = \(\frac{1}{4}\)
Hence , Events A & B are Independent events.
So, (b) is correct.

Question 68.
The probability of getting atleast one 6 from 3 throws of a perfect die is [1 Mark, June 2017]
(a) \(\frac{5}{6}\)
(b) \(\left(\frac{5}{6}\right)^3\)
(c) 1 – \(\left(\frac{1}{6}\right)^3\)
(d) 1 – \(\left(\frac{5}{6}\right)^3\) [1 Mark, June 2017]
Solution:
(d) 1 – \(\left(\frac{5}{6}\right)^3\) [1 Mark, June 2017]
(d) is correct
n = 3 (Trials)
P = Prob. of getting 6 in 1 trial = \(\frac{1}{6}\)
q = 1 – p = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
P(x ≥ 1) = 1 – P(x < 1)
= 1 – P (x = 0) = 1 – ³C₀. P⁰. q³
= 1 – 1.1.(5/6)³ = 1 – (5/6)³

Question 69.
For any two events A and B
(a) P(A – B) = P(A) – P(B)
(b) P(A – B) = P(A) – P(A ∩ B)
(c) P(A – B) = P(B) – P(A ∩ B)
(d) P(B – A) = P(B) + P(A ∩ B)
Solution:
(b) P(A – B) = P(A) – P(A ∩ B)

Question 70.
If P(A) = \(\frac{2}{3}\), P(B) = \(\frac{1}{4}\), P(A ∩ B) = \(\frac{1}{12}\), then P\(\left(\frac{\mathrm{B}}{\mathrm{A}}\right)\) = ____
(a) \(\frac{1}{8}\)
(b) \(\frac{7}{8}\)
(c) \(\frac{1}{3}\)
(d) \(\frac{2}{5}\)
Solution:
(a) \(\frac{1}{8}\)
(a) is correct
p(B/A) = \(\frac{P(A \cap B)}{P(A)}\)
= \(\frac{1 / 12}{2 / 3}\) = \(\frac{1}{12} \times \frac{3}{2}\) = \(\frac{1}{8}\)

Question 71.
For the events A & B if P(A) = \(\frac{1}{2}\),P(B) = \(\frac{1}{3}\) and P(A ∩ B) = \(\frac{1}{4}\) then P\(\left(\frac{A}{B}\right)\) = [1 Mark, Dec. 2017]
(a) 1/2
(b) 1/6
(c) 2/3
(d) 3/4
Solution:
(d) 3/4

Question 72.
If A & B are two mutually exclusive events such that P(A ∪ B) = \(\frac{2}{3}\), P(A) = \(\frac{2}{5}\), then P (B) : [1 Mark, Dec. 2017]
(a) 4/15
(b) 4/9
(c) 5/9
(d) 7/15
Solution:
(a) 4/15
P(A ∪ B) = P(A) + P(B)
[∵ A & B are two mutually exclusive events]
\(\frac{2}{3}\) = \(\frac{2}{5}\) + P(B)
or; P(B) = \(\frac{2}{3}\) – \(\frac{2}{5}\) = \(\frac{10-6}{15}\) = \(\frac{4}{15}\)

Question 73.
If a brother and a sister are applied for 2 vacancies in the same post. The probability that brother will select is 1/7 and that of sister is 1/5, then the probability that
(i) Both will select
(ii) Only one will select,
(iii) None of them will select: [1 Mark, Dec. 2017]
(a) \(\frac{1}{35}\), \(\frac{10}{35}\), \(\frac{24}{35}\)
(b) \(\frac{24}{35}\), \(\frac{7}{35}\), \(\frac{14}{35}\)
(c) \(\frac{3}{35}\), \(\frac{24}{35}\), \(\frac{11}{35}\)
(d) \(\frac{24}{35}\), \(\frac{6}{35}\), \(\frac{20}{35}\)
Solution:
(a) \(\frac{1}{35}\), \(\frac{10}{35}\), \(\frac{24}{35}\)

Let A and B are events of selection of brother and sister respectively.
∵ Both events are independent.

(i) P(Both selected) = P(A∩B) = P(A) . P(B)
= \(\frac{1}{7}\) • \(\frac{1}{5}\) = \(\frac{1}{35}\)

(ii) P(Only one will be selected]
= {P(A) – P(A ∩ B)} + {P(B) – P(A ∩ B)}
= \(\frac{1}{7}\) – \(\frac{1}{35}\) + \(\frac{1}{5}\) – \(\frac{1}{35}\)
= \(\frac{1}{5}\) + \(\frac{1}{7}\) – \(\frac{2}{35}\)
= \(\frac{7+5-2}{35}\) = \(\frac{10}{35}\)

(iii) P(None of them will be selected)
= P(A’) • P(B’) = (1 – \(\frac{1}{7}\)) • (1 – \(\frac{1}{5}\))
= \(\frac{6}{7}\) × \(\frac{4}{5}\) = \(\frac{24}{35}\)

Question 74.
If 4 letters are put randomly among the 4 envelopes then the probability that all are not put in correct envelopes :
(a) 1/24
(b) 1
(c) 23/24
(d) 9/24 [1 Mark, June 2018]
Solution:
(c) 23/24
n(s) = 4! = 24
Let E = Events of putting letter in right envelop.
∴ n(E) = 1.1.1.1 = 1
P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{1}{24}\)
P(E’) = 1 – 1/24 = 23/24

Question 75.
Two broad divisions of probability are :
(a) Subjective probability and objective probability
(b) Deductive probability and mathematical probability
(c) Statistical probability and mathematical probability
(d) None of these [1 Mark, May 2018]
Solution:
(a) Subjective probability and objective probability

Two broad divisions of Probability are

1. Subjective Probability
2. Objective Probability

Question 76.
The term “chance” and probability are synonyms :
(a) True
(b) False
(c) Both
(d) None [1 Mark, May 2018]
Solution:
(a) True

Question 77.
The theorem of Compound Probability states that for any two events A and B
(a) P(A ∩ B) = P(A) × P(B/A)
(b) P(A ∪ B) = P(A) × P(B/A)
(c) P(A ∩ B) = P(A) × P(B)
(d) P(A ∪ B) = P(A) + P(B) – P(A ∩ B) [CA (F) May 2018]
Solution:
(a) P(A ∩ B) = P(A) × P(B/A)
The theorem of Compound Probability states that for two events A and B
P(A ∩ B) = P(A) × P(B/A)

Question 78.
Variance of random variable x is given by
(a) E(X – µ)²
(b) E[X – E(X)]²
(c) E(X² – µ)
(d) (a) or (b)
Solution:
(d) (a) or (b)
Variance of a random variable x is given by
V(X) = E(X – µ)²
or
V(x) = E[X – E(X)]²
Note : ∵ µ = E(X)

Question 79.
What is the probability of having at least one ‘six’ perfect die?
(a) 5/6
(b) (5/6)³
(c) 1 – (1/6)³
(d) 1 – (5/6)³
Solution:
(d) 1 – (5/6)³

For a die Probability of getting Six
P(A) = \(\frac{1}{6}\) = p
P\((\overline{\mathrm{A}})\) = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\) = q
Here n = 3
P(getting at least ‘ 1 ’ Six) = P(X ≥ 1)
= 1 – P(X < 1)
= 1 – P(X = 0)
= 1 – ³C₀.\(\left(\frac{1}{6}\right)^0 \cdot\left(\frac{1}{6}\right)^{3-0}\)
= 1 – 1 × 1 × \(\left(\frac{5}{6}\right)^3\)
= 1 – \(\left(\frac{5}{6}\right)^3\)

Question 80.
Sum of all probabilities of mutually exclusive and exhaustive events is equal to
(a) 0
(b) 1/2
(c) 1/4
(d) 1
Solution:
(d) 1

If events are mutually exclusive and exhaustive events then Sum of all probabilities = 1.

Question 81.
If P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{3}\), and P(A ∩ B) = \(\frac{1}{4}\) then P(A ∪ B) is equal to
(a) \(\frac{11}{12}\)
(b) \(\frac{7}{12}\)
(c) \(\frac{10}{12}\)
(d) \(\frac{1}{6}\) [1 Mark, Noc. 2018]
Solution:
(b) \(\frac{7}{12}\)
P(A ∪ B) = P(A) + P(B) – P(A∩B)
= \(\frac{1}{6}\) + \(\frac{1}{3}\) – \(\frac{1}{4}\) = \(\frac{6+4-3}{12}\) = \(\frac{7}{12}\)

Question 82.
Two different dice are thrown simultaneously, then the probability, that the sum of two numbers appearing on the top of dice is 9 is [1 Mark, Nov. 2018]
(a) \(\frac{1}{9}\)
(b) \(\frac{8}{9}\)
(c) \(\frac{7}{9}\)
(d) None of the above
Solution:
(a) \(\frac{1}{9}\)
n(S) = 6² = 36
E = {(3, 6), (4, 5), (5, 4), (6, 3)}
n(E) = 4
∴ P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{4}{36}\) = \(\frac{1}{9}\)

Question 83.
If (A ∪ B) = 0.8 and P(A ∩ B) = 0.3 then P\((\overline{\mathrm{A}})\) + P\((\overline{\mathrm{B}})\) is equal to: [1 Mark, Nov. 2018]
(a) 0.3
(b) 0.5
(c) 0.9
(d) 0.7
Solution:
(c) 0.9

P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
or; 0.8 = P(A) + (B) – 0.3
or; P(A) + P(B) = 0.8 + 0.3 = 1.1
∴ P\((\overline{\mathrm{A}})\) + P\((\overline{\mathrm{B}})\) = 1 – P(A) + 1 – P(B)
= 2 – [P(A) + P(B)]
= 2 – 1.1 = 0.9

Question 84.
The probability that a leap year has 53 Wednesday is
(a) \(\frac{2}{7}\)
(b) \(\frac{3}{5}\)
(c) \(\frac{1}{7}\)
(d) \(\frac{2}{3}\) [1 Mark, Nov. 2018]
Solution:
(a) \(\frac{2}{7}\)

1 Leap year = 366 days = 52 weeks & 2 days
S = {(Sun ; Mon); (Mon ; Tues);
(Tues ; Wed); (Wed ; Thurs) ;
(Thurs ; Fri); (Fri; Sat); (Sat; Sun)
∴ n(S) = 7
E = Event of getting Wednesday = {Tues ; Wed); (Wed ; Thurs)}
n(E) = 2
∴ P(E) = \(\frac{n(E)}{n(S)}\) = \(\frac{2}{7}\)

Question 85.
A coin is tossed six times, then the probability of obtaining heads and tails alternatively is
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{32}\)
(a) \(\frac{1}{64}\)
(a) \(\frac{1}{16}\)
Solution:
(b) \(\frac{1}{32}\)

P(Head & Tail alternatively) = P(H). P(T). P(H). P(T). P(H). P(T). + P(T) . P(H). P(T). P(H). P(T). P(H) = \(\left(\frac{1}{2}\right)^6+\left(\frac{1}{2}\right)^6\)
= \(\frac{1}{64}\) + \(\frac{1}{64}\) = \(\frac{2}{64}\) = \(\frac{1}{32}\)

Question 86.
Ram is known to hit a target in 2 out of 3 shots where as Shyam is known to hit the same target in 5 out of 11 shots. What is the probability that the target would be hit if they both try?
(a) \(\frac{9}{11}\)
(b) \(\frac{6}{11}\)
(c) \(\frac{10}{33}\)
(d) \(\frac{3}{11}\) [1 Mark, Nov. 1018]
Solution:
(a) \(\frac{9}{11}\)
P(Ram) = P(R) = \(\frac{2}{3}\)
P(R’) = 1 – \(\frac{2}{3}\) = \(\frac{1}{3}\)
and P(Shyam) = P(S) = \(\frac{5}{11}\)
⇒ P(S’) = 1 – \(\frac{5}{11}\) = \(\frac{6}{11}\)
∴ P (Target hit) = 1 – P (Target not hit)
⇒ 1 – P(R’).p(S’) = 1 – \(\frac{1}{3}\).\(\frac{6}{11}\)
= 1 – \(\frac{2}{11}\) = \(\frac{9}{11}\)

Question 87.
The probability that a student is not a swimmer is \(\frac{1}{5}\), then the probability that out of five students four are swimmer is
(a) \(\left(\frac{4}{5}\right)^4\left(\frac{1}{5}\right)\)
(b) \({ }^5 C_1\left(\frac{1}{5}\right)^4\left(\frac{4}{5}\right)\)
(c) \({ }^5 C_4\left(\frac{4}{5}\right)^4\left(\frac{1}{5}\right)\)
(d) None
Solution:
(c) \({ }^5 C_4\left(\frac{4}{5}\right)^4\left(\frac{1}{5}\right)\)

Given that
let q = Prob. that a student is not a swimmer = \(\frac{1}{5}\)
∴ P = Prob. (Swimmer) = 1 – q = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
n = 5
P(X = 4) = ⁵C₄ • p⁴ • q¹
= \({ }^5 \mathrm{C}_4 \cdot\left(\frac{4}{5}\right)^4 \cdot\left(\frac{1}{5}\right)^1\)

Question 88.
If Y ≥ x then mathematical expectation is
(a) E (X) ≥ E (Y)
(b) E (X) ≤ E (Y)
(c) E (X) = E (Y)
(d) E (X) . E (Y) = 1 [1 Mark, June 2019]
Solution:
(b) If y ≥ x then E (y) ≥ E (x)
E (x) ≤ E (y)

Question 89.
Two event A and B are such that they do not occurs simultaneously then they are called ____ events
(a) Mutually exhaustive
(b) Mutually exclusive
(c) Mutually independent
(d) Equally likely [1 Mark, June 2019]
Solution:
(b) Mutually exclusive

Question 90.
According to Baye’s Theorem. P(E_k/A) = \(\frac{P\left(E_K\right) P\left(A / E_K\right)}{\sum_{i=1}^n P\left(E_1\right) P\left(A / E_1\right)}\)
(a) E₁, E₂ ………… are mutually exclusive
(b) P(E/A₁), P(E/A₂), ……… are equal to 1
(c) P(A₁/E), P(A₂/ E), …….. are equal to 1
(d) A & E₁’s are disjoint sets.
Solution:
(b) According to Baye’s Theorem

Where, E₁, E₂, E₃,…….. are Mutually Exclusive.

Question 91.
If a coin is tossed 5 times then the probability of getting Tail and Head Occurs alternatively is
(a) \(\frac{1}{8}\)
(b) \(\frac{1}{16}\)
(c) \(\frac{1}{32}\)
(d) \(\frac{1}{64}\) [1 Mark, June 2019]
Solution:
(b) \(\frac{1}{16}\)

P(getting tail and Head occurs Alternatives) = P(HTHTH) or P(THTHT)
= (\(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\)) + (\(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\))
= \(\frac{1}{32}\) + \(\frac{1}{32}\) = \(\left(\frac{1+1}{32}\right)\)
= \(\frac{2}{32}\) = \(\frac{1}{16}\)

Question 92.
When 2 – dice are thrown Simultaneously then the probability of getting at least one 5 is
(a) \(\frac{11}{36}\)
(b) \(\frac{5}{36}\)
(c) \(\frac{8}{15}\)
(d) \(\frac{1}{7}\) [1 Mark, June 2019]
Solution:
(a) If two dice are thrown then sample space n(S) = 36
Events ‘A’ = getting at least one ‘5’
‘A’ = {(5, 1) ; (5, 2); (5, 3) ; (5, 4); (5, 5) ; (5, 6) (1, 5) ; (2, 5); (3, 5); (4. 5) ; (6, 5)}
n (A) = 11
n(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{11}{36}\)