These Measures of Dispersion – CA Foundation Statistics Notes are designed strictly as per the latest syllabus and exam pattern.
Measures of Dispersion – CA Foundation Statistics Notes
Previous Year Exam Questions
Question 1.
A student obtained the mean and standard deviation of 100 observations as 40 and 5.1 respectively. It was later discovered that he had wrongly copied down an observation as 50 instead of 40. The correct standard deviation is _______ [1 Mark, Nov. 2006]
(a) 5
(b) 6
(c) 3
(d) 7
Solution:
N = 100, In correct \(\overline{\mathrm{X}}\) = 40 & σ = 5.1
Incorrect obs. = 50, Correct obs.= 40
correct mean \(\overline{\mathrm{X}}\) = \(\frac{100 \times 40-50+40}{100}\) = 39.9
∴ σ2 = \(\frac{\sum \mathrm{x}^2}{\mathrm{~N}}\) (\(\overline{\mathrm{X}}\))2 ; ∴ (5.1)2 = \(\frac{\sum \mathrm{x}^2}{100}\) – (40)2
or; 26.01 + 1600 = \(\frac{\sum \mathrm{x}^2}{100}\)
Incorrect Σ X2 = 1626.01 x 100 = 162601
∴ Correct Σ X2 = 162601 – 502 + 402 = 1,61,701
∴ Correct σ = \(\sqrt{\frac{161701}{100}-(39.0)^2}\) = 5
(a) is correct.
![]()
Question 2.
If two samples of sizes 30 and 20 have means as 55 and 60 and variances as 16 and 25 respectively, then what would be the S.D. of the combined sample size 50? [1 Mark, Feb. 2007]
(a) 5.33
(b) 5.17
(c) 5.06
(d) 5
Solution:
(c) is Correct
Given N1 = 30; N2 = 20; \(\overline{X_1}\) = 55; \(\overline{X_2}\) = 60
σ12 =16 ; σ22 = 25.; σ12 = ?
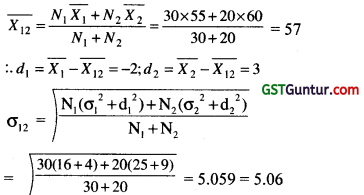
Question 3.
If two variables x and y are related by 2X + 3Y – 7 = 0 and the mean and mean deviation about mean of X are 1 and 0.3 respectively, then the co-efficient of mean deviation of Y about mean is : [1 Mark, Feb. 2007]
(a) -5
(b) 4
(c) 12
(d) 50
Solution:
(c) If Y = a + bX , a and b being constant, then M.Dy = |b| ,(M.Dx)
(Since M.D. changes due to change in scale)
∴ y = –\(\frac{2}{3}\) X + \(\frac{7}{3}\)
M.Dy = |-\(\frac{2}{3}\)| (M.Dx) = (\(\frac{2}{3}\)) × 0.3 = 0.2
Also 2X + 3Y – 7 = 0 2
\(\overline{\mathrm{X}}+3 \overline{\mathrm{Y}}\) – 7 = 0 (Since, the A.M. is affected by change of origin as well as change of scale)
\(\overline{\mathrm{Y}}\) = – \(\frac{2}{3}\) \(\overline{\mathrm{X}}\) + \(\frac{7}{3}\)
\(\overline{\mathrm{Y}}\) = – \(\frac{2}{3}\) x 1 \(\frac{7}{3}\) = \(\frac{5}{3}\) (Given \(\overline{\mathrm{X}}\) = 1)
Coefficient of mean deviation of Y about mean
= \(\frac{M \cdot D_{\overline{\mathrm{Y}}}{\bar{y}}\) × 100 = \(\frac{0.2}{5 / 3}\) × 100 = 12
![]()
Question 4.
Measures of dispersion are called averages of the _________ order : [1 Mark, May 2007]
(a) 1st
(b) 2nd
(c) 3rd
(d) None
Solution:
(b) is correct
Question 5.
For a set of 100 observations, taking assumed mean as 4, the sum of the deviations is -11cm, and the sum of the squares of these deviations is 275 cm2. The coefficient of variation is : [1 Mark, May 2007]
(a) 41.13%
(b) 42.13%
(c) 40.13%
(d) None
Solution:
(a) Given N = 100 ; A = 4 ; Σ d = -11; Σ d2 = 275

= \(\frac{1.6}{3.89}\) × 100 = 41.13%
Question 6.
are used for measuring central tendency, dispersion and skewness: [1 Mark, Aug. 2007]
(a) Median
(b) Deciles
(c) Percentiles
(d) Quartiles
Solution:
(d) is correct.
![]()
Question 7.
Which of the following companies A or B is more consistent so far as the payment of dividend is concerned? [1 Mark, Aug. 2007]

(a) A
(b) B
(c) Both A & B
(d) Neither A nor B
Solution:
(a)

∴ σB = 4.54
C.VB = \(\frac{4.54}{9.125}\) × 100 = 49.75
Similarly, C . VA < C . VB
Company A is more consistent than B.
![]()
Question 8.
What is the coefficient of range for the following distribution? [1 Mark, Aug. 2007]

(a) 22%
(b) 50%
(c) 75.82%
(d) 72.46%
Solution:
(d) 1st We convert Class – Interval into a continuous data
LCB = S = 9.5; HCB = L = 59.5
∴ Range = L – S = 59.50 – 9.50 = 50
Coefficient of Range = \(\frac{L-S}{L+S}\) × 100
= \(\frac{59.50-9.50}{59.50+9.50}\) × 100 = \(\frac{50}{69}\) × 100 = 72.46%
Question 9.
A sample of 35 observations has the mean 80 and S.D. as 4. A second sample of 65 observations from the same population has mean 70 and S.D. 3. The S.D. of the combined sample is : [1 Mark, Nov. 2007]
(a) 5.85
(b) 5.58
(c) 10.23
(d) None of these
Solution:
(a)

TRICKS : Use Calculator
![]()
Question 10.
If X and Y are related as 3X – 4Y = 20 and the quartile deviation of X is 12, then the quartile deviation of Y is : [1 Mark, Nov. 2007]
(a) 14
(b) 15
(c) 16
(d) 9
Solution:
(d)
If y = a + bx, a and b being constant, then Q.D.y = |b|, . Q . Dx
3x – 4y = 20 or y = \(\frac{3}{4}\) X + 5
Q.Dy = |\(\frac{3}{4}\)| × 12 = 9
Question 11.
The best measure of dispersion is: [1 Mark, Feb. 2008]
(a) Q.D.
(b) M.D.
(c) Range
(d) S.D.
Solution:
(d) is correct.
![]()
Question 12.
If the mean and S.D. of X are a and b respectively, then the S.D. of \(\frac{x-a}{b}\) [1 Mark, Feb. 2008]
(a) a/b
(b) -1
(c) 1
(d) ab
Solution:
(c) Let y = \(\frac{x-a}{b}\)
y = \(\frac{X}{b}-\frac{a}{b}\)
σy = \(\left|\frac{1}{b}\right|\)σx = \(\frac{1}{b}\) × b = 1
Question 13.
Suppose a population A has 100 observations 101,102,103,200 and another population B has 100 observations 151, 152, 153, ………… 250. If VA and VB represents the variance of the two populations respectively, then VA/ VB = : _________ [1 Mark, Feb. 2008]
(a) 9/4
(b) 1
(c) 4/9
(d) 2/3
Solution:
(b)
RULE : SD doesn’t change with respect to the change of origin (+ /-).
Population A : S.D. of 101, 102, 103, ……….. 200.
Let its SD = σ
50 is added to all observations; we get data : 151, 152, ……….. 250
Its SD = σ (also).
Hence SD of data B = σ
\(\frac{V_A}{V_B}\) = \(\frac{\sigma^2}{\sigma^2}\) = 1
TRICKS : After subtraction both data are exactly same; So ratio of variances is 1.
![]()
Question 14.
The Mean and S.D. for group of 100 observations are 65 and 7.03 respectively If 60 of these observations have mean and S.D. as 70 and 3 respectively, what is the S.D. for the group comprising 40 observations? [1 Mark, June 2008]
(a) 2.03
(b) 4.03
(c) 8.03
(d) 9.33
Solution:
(b)

Question 15.
The quartile deviation for the data is : [1 Mark, June 2008]

(a) 1/4
(b) 1/2
(c) 1
(d) 0
Solution:
(c)
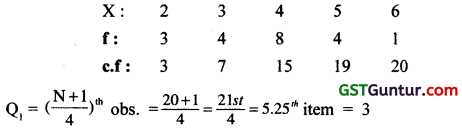
and Q3 = \(\frac{3(N+1)^{t h}}{4}\) item = 15.75th item = 5
So, Q.D. = \(\frac{1}{2}\) (Q3 – Q1) = \(\frac{1}{2}\) (5 – 3) = 1
![]()
Question 16.
If X and Y are two random variables then v (x + y) is : [1 Mark, Dec. 2008]
(a) v (x) + v (y)
(b) v (x) + v (y) – 2 v (x, y)
(c) v (x) + v (y) + 2 v (x, y)
(d) v (x) – v (y)
Solution:
(a)
Since, Variance of sum of two random variables is equal to the sum of their variances
i.e. V(x +y) = V(x) + V(y) for any two random variables x and y.
Question 17.
Mean and S. D of X is 50 and 5 respectively. Find mean and S.D. of \(\frac{X-50}{5}\). [1 Mark, Dec. 2008]
(a) (1, 0)
(b) (0, 1)
(c) (1, 1)
(d) (0, -1)
Solution:
(b)
\(\overline{\mathrm{X}}\) = 50 and σx = 5
Let Y = \(\frac{\overline{\mathrm{X}} -50}{5}\) = \(\frac{\overline{\mathrm{X}}}{5}\) – 10 ……………. (1)
RULE AM changes due to the change of origin and or scale,
So, \(\bar{y}=\frac{\bar{x}-50}{5}=\frac{50-50}{5}\) = 0
RULE :- S.D does not change due to the change of origin but changes due to the change of scale.
σy = |\(\frac{1}{5}\)| σx = \(\frac{1}{5}\) × 5 = 1
![]()
Question 18.
Mean and S. D. of a given set of observations is 1,500 and 400 respectively. If there is an increment of 100 in the first year and each observation is hiked by 20% in 2nd year, then find new mean and S.D. [1 Mark, Dec. 2008]
(a) 1920,480
(b) 1920,580
(c) 1600,480
(d) 1600,400
Solution:
(a)
\(\overline{\mathrm{X}}\) = 1500, σ = 400
After 1st year,
Mean = 1500 + 100 = 1600
S.D. = 400
After 2nd year,
Mean
1600 × 1.20
= 1,920
S.D.
400 × 1.20
= 480
![]()
Question 19.
If 5 is subtracted from each observation of some certain item then its co-efficient of variation is 10% and if 5 is added to each item then its coefficient of variation is 6%. Find original coefficient of variation. [1 Mark, Dec. 2008]
(a) 8%
(b) 7.5%
(c) 4%
(d) None of these
Solution:
(b)
Coefficient of variation CV. = \(\frac{\sigma}{\text { Mean }}\) × 100
Mean
RULE : S.D. does not change but Mean changes due to the change of origin.
Let original S.D. = σ and mean = \(\overline{\mathrm{x}}\)
∴ Case I \(\frac{\sigma}{\bar{x}-5}\) × 100 = 10 ………………… (1)
Case II \(\frac{\sigma}{\bar{x}+5}\) × 100 = 6 ………………. (2)
Dividing (2) by (1), we get
\(\frac{\overline{X}-5}{\overline{X}+5}\) = \(\frac{6}{10}\) ; Solving it, we get
\(\overline{\mathrm{x}}\) = 20 and σ = 1.5
Original C.V = \(\frac{1.5}{20}\) × 100 = 7.5%
Question 20.
Inter Quartile Range is __________ of Quartile Deviation. [1 Mark, Dec. 2009]
(a) Half
(b) Double
(c) Triple
(d) Equal
Solution:
(b)
Since, Quartile Deviation or
Semi-inter quartile Range = \(\frac{Q_3-Q_1}{2}\)
Inter-Quartile Range = Q3 – Q1 = 2.QD
![]()
Question 21.
The sum of squares of deviation from mean of 10 observations is 250. Mean of the data is lO.Find the co-efficient of variation. [1 Mark, Dec. 2009]
(a) 10%
(b) 25%
(c) 50%
(d) 0%
Solution:
(c)
Given , N = 10 ; Σ (X – \(\overline{\mathrm{X}}\))2 = 250
Mean = 10
S.D. = \(\sqrt{\frac{\sum(X-\overline{X})^2}{N}}\) = \(\sqrt{\frac{250}{10}}\) = 5
So, CV = \(\frac{S . D .}{M e a n}\) × 100 = \(\frac{5}{10}\) × 100 = 50%
Question 22.
If L1 = highest observation and L2 = smallest observation, then Coefficient of Range = ________ [1 Mark, Dec. 2009]

Solution:
(b) Coefficient of Range = \(\frac{L-S}{L+S}\) × 100 (Formula)
= \(\frac{L_1-L_2}{L_1+L_2}\) × 100
![]()
Question 23.
The equation of a line is 5X + 2Y = 17. Mean deviation of Y about mean is 5. Calculate mean deviation of X about mean. [1 Mark, Dec. 2009]
(a) -2
(b) 2
(c) -4
(d) None
Solution:
(b) TRICKS : +5 MDx = + 2 MDy
5 MDx = 2 × 5
MDx = 2
Question 24.
If variance of x is 5, then find the variance of (2 – 3x) [1 Mark, Dec. 2009]
(a) 10
(b) 45
(c) 5
(d) -13
Solution:
(b)
Let Y = 2 – 3X
σy = |-3|σx = 3 . \(\sqrt{5}\)
Var.(Y) = (3 . \(\sqrt{5}\))2 = 9 × 5 = 45
![]()
Question 25.
The variance of data : 3, 4, 5, 8 is ________ [1 Mark, Dec. 2010]
(a) 4.5
(b) 3.5
(c) 5.5
(d) 6.5
Solution:
(b)
X : 3, 4, 5, 8
Σ X = 20 ; Σ X2 = 9 + 16 + 25 + 64 = 114
variance \(\frac{\sum \mathrm{X}^2}{\mathrm{n}}-\left(\frac{\sum \mathrm{X}}{\mathrm{n}}\right)^2\)
= \(\frac{114}{4}\) – 25 = 3.5
Question 26.
Given the observations :4, 9, 11, 14, 37. The Mean deviation about the Median is ______ [1 Mark, Dec. 2010]
(a) 11
(b) 8.5
(c) 7.6
(d) 745
Solution:
(C)
4, 9, 11, 14, 37
Median = Middle obs. = 11

Σ |d| = 38
Mean deviation about median
M.D. = \(\frac{\sum|d|}{n}\) = \(\frac{3}{2}\) = 7.6
![]()
Question 27.
If all observations in a distribution are increased by 6, then the variance of the series will be _________. [1 Mark, Dec. 2010]
(a) Increased
(b) Decreased
(c) Unchanged
(d) None of these
Solution:
(c)
RULE SD does not w.r.t. origin.
So; Variance will also remain unchanged.
Question 28.
The standard deviation of the weights (in kg.) of the student of a class of 50 students was calculated to be 4.5 kg. Later on it was found that due to some fault in weighing machine, the weight of each student was under measured by 0.5 kg. The Correct standard deviation of the weight will be: [1 Mark, Dec. 2011]
(a) Less than 4.5
(b) Greater than 4.5
(c) Equal to 4.5
(d) Cannot be determined
Solution:
(c)
RULE : S.D remains unaffected due to a change of origin but changes with respect to scale.
So, correct S.D. of 50 students = 4.5
![]()
Question 29.
For Normal distribution the relation between quartile deviation (Q.D.) and standard deviation (S.D.) is _________ [1 Mark, Dec. 2011]
(a) Q.D > S.D
(b) Q.D < SD
(c) Q.D = S.D
(d) None of the above
Solution:
(b) Since; Q.D = \(\frac{2}{3}\)
S.D ⇒ Q.D < S.D
Question 30.
If standard deviation of first ‘n’ natural numbers is 2 then the value of ‘n’ is ________ [1 Mark, June 2010]
(a) 10
(b) 7
(c) 6
(d) 5
Solution:
(b)
S.D. of 1st .n. natural Numbers = \(\sqrt{\frac{n^2-1}{12}}\) \(\frac{2}{1}\)
= \(\sqrt{\frac{n^2-1}{12}}\) ,
OR, 4 = \(\frac{n^2-1}{12}\)
OR, n2 – 1 = 48
OR, n2 = 49 ⇒ n = 7
TRICKS : Go by choices.
![]()
Question 31.
The standard deviation is independent of change of ________ [1 Mark, June 2010]
(a) Scale
(b) Origin
(c) Both origin and scale
(d) None of these
Solution:
(b)
Question 32.
If Standard deviation of X is σ, then Standard deviation of \(\frac{a x+b}{c}\), where a, b and c are arbitrary constants, will be __________ [1 Mark, Dec. 2012]
(a) σ
(b) \(\frac{a \sigma+b}{c}\)
(c) \(\left|\frac{a}{c}\right|\) . σ
(d) \(\left|\frac{a}{c}\right|\) σ
Solution:
S.D. of X = σ
Let y = \(\frac{a x+b}{c}\) = \(\frac{a x}{c}+\frac{b}{c}\)
S.D. of y = \(\left|\frac{a}{c}\right|\)
S.D. of x = \(\left|\frac{a}{c}\right|\) σ
![]()
Question 33.
Which of the following measures of dispersion is used for calculating the consistency between two series? [1 Mark, Dec. 2012]
(a) Quartile deviation
(b) Standard Deviation
(c) Coefficient of variation
(d) None of them
Solution:
(c)
Coefficient of variation (CV) is used for calculating the consistency between two series.
Question 34.
Σ x2 = 3390, n = 30, σ = 7; then \(\overline{\mathrm{X}}\) = _______ [1 Mark, June 2013]
(a) 113
(b) 210
(c) 8
(d) None
Solution:
(c) is correct
∵ σ2 = \(\frac{\sum \mathrm{x}^2}{\mathrm{~N}}\) = (\(\overline{\mathrm{X}}\))2
or 49 = \(\frac{3390}{30}\) – (\(\overline{\mathrm{X}}\))2
or (X)2 = 113 – 49 = 64
∴ \(\overline{\mathrm{X}}\) = 8
![]()
Question 35.
If the mean of frequency distribution is 100 and coefficient of variation is 45% then standard deviation is _______. [1 Mark, June 2013]
(a) 45
(b) 0.45
(c) 0.045
(d) None
Solution:
(a) is correct
CV = \(\frac{\sigma}{\overline{\mathrm{X}}}\) × 100
or, 45 = \(\frac{\sigma}{100}\) × 100, σ = 45
Question 36.
If Arithmetic Mean = \(\frac{8+4}{2}\) then variance is _______. [1 Mark, Dec. 2013]
(a) 2
(b) 6
(c) 1
(d) 4
Solution:
(d) is correct
Arithmetic mean = \(\frac{8+4}{2}\)
∴ Numbers are 8; 4
∴ SD of 8 & 4 = \(\frac{1}{2}\)|8 – 4| = 2
Variance – SD2 = 4
![]()
Question 37.
Coefficient of mean deviation about mean for the first 9 natural numbers is: [1 Mark, Dec. 2013]
(a) \(\frac{200}{9}\)
(b) 80
(c) \(\frac{400}{9}\)
(4) 50
Solution:
(c) is correct
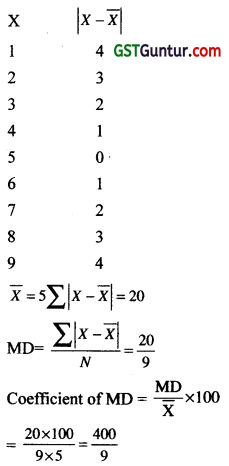
Question 38.
Mean = 5, S.D = 2.6, Median = 5,QD = 1.5 then coefficient of Q.D is: ________ [1 Mark, Dec. 2013]
(a) 35
(b) 39
(c) 30
(d) 32
Solution:
(C) is correct
∵ Mean = Median =5
∴ Data is symmetrical
∴ M = \(\frac{Q_3+Q_1}{2}\) = 5
∴ Q3 + Q1 = 10
Coefficient of QD = \(\frac{Q_3-Q_1}{Q_3+Q_1}\) × 100
= \(\frac{2 \times Q D}{Q_3+Q_1}\) × 100 = \(\frac{2 \times 1.5}{10}\) × 100
= 30.
![]()
Question 39.
The difference between maximum and minimum value of the data is known as: [1 Mark, Dec. 2013]
(a) Range
(b) Size
(c) Width
(d) Class
Solution:
(a)
Range = L – S.
Question 40.
The formula for range of middle 50% items of a series is _________. [1 Mark, June 2014]
(a) Q3 – Q1
(b) Q3 – Q2
(c) Q2 – Q1
(d) \(\frac{Q_3-Q_1}{2}\)
Solution:
(a) is correct
Range of Middle 50% items
= Inter Quartile Range
= Q3 – Q1
![]()
Question 41.
What will be the probable value of mean deviation? When Q3 = 40 and Q1 = 15 [1 Mark, June 2014]
(a) 17.50
(b) 18.75
(c) 15.00
(d) None of the above
Solution:
(c) is correct
6QD = 5 MD = 4 SD
or \(\frac{6 \cdot\left(Q_3-Q_1\right)}{2}\) = 5 MD
or 3(40 – 15) = 5 MD
or MD = 15.00
Question 42.
1st quartile is 142 Semi-inter Quartile 18. Then median is _________. [1 Mark, Dec. 2014]
(a) 151
(b) 160
(c) 178
(d) None
Solution:
(b) is correct.
∴ Q1 = 142
Semi-inter Quartile Range
= QD = \(\frac{Q_3-Q_1}{2}\) = 18
∴ Q3 – Q1 = 36
Q3 – 142 = 36
Q3 = 142 + 36 = 178
Median = M = \(\frac{Q_3+Q_1}{2}\) = \(\frac{178+142}{2}\) = 160
(Remember: Here it has assumed as symmetrical)
![]()
Question 43.
Q.D is ________. [1 Mark, Dec. 2014]
(a) 2/3 .SD
(b) 4/5 SD
(c) 5/6 S.D
(d) None
Solution:
(a) is correct.
∴ 6QD = 5MD – 4SD
QD = \(\frac{4}{6}\) SD = \(\frac{2}{3}\) SD
Question 44.
Co-efficient of QD is equal to ______ [1 Mark, June 2015]
(a) \(\frac{Q D}{M}\) × 100
(b) \(\frac{Q D}{\bar{x}}\) × 100
(c) \(\frac{Q D}{Z}\) × 100
(d) None
Solution:
(a) is correct.
Co-efficient of QD = \(\frac{Q_3-Q_1}{Q_3+Q_1}\) × 100
= \(\frac{\frac{Q_3-Q_1}{2}}{\frac{Q_3+Q_1}{2}}\) × 100 = \(\frac{Q D}{M}\) × 100
where M = \(\frac{Q_3+Q_1}{2}\) (Symmetrical)
![]()
Question 45.
If every observation is increased by 5 then _________. [1 Mark, June 2015]
(a) SD increases by 5
(b) MD increases by 5
(c) QD increases by 5
(d) None affected
Solution:
(d) is correct.
Rule : The value of QD ; MD ; SD ; RANGE does not change with respect to the change of origin.
Question 46.
The SD of X is known to be 10 then the SD of (50 + 5 x) is _________. [1 Mark, June 2015]
(a) 50
(b) 100
(c) 10
(d) 500
Solution:
SD of (50 + 5x)
= 5 × SD of x
= 5 × 10 = 50
![]()
Question 47.
Find the range of 6, 5, 4, 3, 1, 3, 6, 10, 8. [1 Mark, Dec. 2015]
(a) 6
(b) 3
(c) 9
(d) 10
Solution:
(c) is correct.
Range = L – S = 10 -1 = 9
Question 48.
Find the mean deviation about mean of 4, 5, 6, 8, 3 : [1 Mark, Dec. 2015]
(a) 7.2
(b) 5.2
(c) 1.44
(d) 1.70
Solution:
(c) is correct.

![]()
Question 49.
If V(x) =23 Find variance of (2x + 10:) [1 Mark, Dec. 2015]
(a) 104
(b) 110
(c) 92
(d) 85
Solution:
(c) is correct.
Var.(X) = σ2 = 23 ; ∴ σ = \(\sqrt{23}\)
SD of (2X + 10)= 2.σ = 2\(\sqrt{23}\)
Var.(2X + 10)=(2\(\sqrt{23}\))2 = 92
Question 50.
The average of 2 numbers is 20 and their standard deviation 5. Find the two numbers? [1 Mark, Dec. 2015]
(a) 15, 25
(b) 30, 40
(c) 10, 15
(d) None of these
Solution:
(a) is correct.
Tricks : Go by choices. For option (a)
AV. = \(\frac{15+25}{2}\) = 20
SD = σ = \(\frac{1}{2}\)|25-15| = 5
It satisfy both conditions which are given in question.
![]()
Question 51.
If Variance = 125.6, \(\overline{X}\) = 40, coefficient of variation = _________ [1 Mark, Dec. 2015]
(a) 28.02
(b) 314
(c) 40.02
(d) None of these
Solution:
(a) is correct.
σ = \(\sqrt{125.6}\) =11.21
C . V = \(\frac{\sigma}{\overline{\mathrm{X}}}\) × 100 = \(\frac{11.21}{40}\) × 100 = 28.02
Question 52.
If same amount is added to or subtracted from all the values of the individual series then the standard deviation and variance both shall be ________. [1 Mark, June 2016]
(a) Changed
(b) Unchanged
(c) Same
(d) None of these
Solution:
(b)
Since, SD does not change with respect to the change of origin. So, variance will also remain unchanged.
![]()
Question 53.
The SD of first n natural numbers is _________ [1 Mark, June 2016]
(a) \(\sqrt{\frac{n^2-1}{12}}\)
(b) \(\sqrt{\frac{n(n+1)}{12}}\)
(c) \(\sqrt{\frac{n(n-1)}{6}}\)
(d) None of these
Solution:
(a)
Question 54.
If mean and coefficient of variation of the marks of n students is 20 and 80 respectively. What will be variance of them [1 Mark, June 2016]
(a) 256
(b) 16
(c) 25
(d) None of these
Solution:
(a)
Given \(\overline{\mathrm{X}}\) = 20; C.V = 80%
∴ C.V. = \(\frac{\sigma}{\overline{\mathrm{X}}}\) × 100
∴ 80 = \(\frac{\sigma}{\overline{\mathrm{X}}}\) × 100
∴ σ = \(\frac{80 \times 20}{100}\) = 16
Variance = σ2 = 162 = 256
![]()
Question 55.
If AM and CV of a random variable X are 10 & 40 respectively, then the variance of (-15 + \(\frac{3 x}{2}\)) : ______. [1 Mark, June 2017]
Solution:
(d) is correct.
Given ; \(\frac{\sigma}{10}\) × 100 = 40
∴ σ = 4
∴ SD of (-15 + \(\frac{3}{2}\)x) = \(\frac{3}{2}\) × SD(x) = \(\frac{3}{2}\) × 4 = 6
∴Variance of (-15 + \(\frac{3}{2}\)x) = 62 = 36
Question 56.
Mean deviation is least when deviations are taken from : [1 Mark, Dec. 2017]
(a) Mean
(b) Median
(c) Mode
(d) None of these
Solution:
(b)
![]()
Question 57.
Mean of a series is equal to 100, coefficient of variation is 45% then the S.D. is _______. [1 Mark, June 2018]
(a) 45
(b) 0.45
(c) 4.5
(d) 40.5
Solution:
(a)
C. V. = \(\frac{\sigma}{\overline{\mathrm{X}}}\) × 100
or 45 = \(\frac{\sigma}{100}\) × 100
σ = 45
Question 58.
Coefficient of variation is a relative measure of _________. [1 Mark, June 2018]
(a) Range
(b) Central Tendency
(c) Dispersion
(d) Q.D.
Solution:
(c)
![]()
Question 59.
\(\frac{\left(Q_3-Q_1\right)}{\left(Q_3+Q_1\right)}\) is known as _________. [1 Mark, May 2018]
(a) Coefficient of Range
(b) Coefficient of Q.D.
(c) Coefficient of S.D.
(d) Coefficient of M.D.
Solution:
(b)
Coefficient of Q.D. = \(\frac{\left(Q_3-Q_1\right)}{\left(Q_3+Q_1\right)}\)
Question 60.
If the S.D. of the 1st n natural Nos. is \(\sqrt{30}\), Then the value of n is ________. [1 Mark, May 2018]
(a) 19
(b) 20
(c) 21
(d) None
Solution:
(a)
Tricks : GBC
For (a)
S.D = \(\sqrt{\frac{n^2-1}{12}}\) = \(\sqrt{\frac{19^2-1}{12}}\) = \(\sqrt{30}\) (true)
Question 61.
If two random variables x and y are related by Y = 2 – 3X, then the SD of Y is given by __________. [1 Mark, May 2018]
(a) -3 × SD of X
(b) 3 × SD of X
(c) 9 × SD of X
(d) 2 × SD of X
Solution:
(b)
S.D of y (σy) = |b| S.D of X(σx)
= |-3| . σx
= 3 σx
![]()
Question 62.
If the variance of 5, 7, 9 and 11 is 4, then the coefficient of variation is ________. [1 Mark, Nov. 2018]
(a) 25
(b) 15
(c) 17
(d) 19
Solution:
(a)
σ2 = 4 ⇒ σ = 2
\(\overline{\mathrm{x}}\) = (5 + 7 + 9 + 11) ÷ 4 = 8
∴ CV = \(\frac{\sigma}{\overline{\mathrm{X}}}\) × 100 = \(\frac{2}{8}\) × 100 = 25%
Question 63.
Standard Deviation for the marks obtained by a student in monthly test in Mathematics (out of 50) as 30, 35, 25, 20, 15 is __________. [1 Mark, Nov. 2018]
(a) 25
(b) 50
(c) \(\sqrt{50}\)
(d) \(\sqrt{30}\)
Solution:
(c)

= \(\sqrt{\frac{3375}{5}-\left(\frac{125}{5}\right)^2}\)
= \(\sqrt{50}\)
![]()
Question 64.
If the standard deviation for the marks obtained by a student in monthly test is 36, then the variance is ________. [1 Mark, Nov. 2018]
(a) 36
(b) 6
(c) 1296
(d) None of the above
Solution:
(c)
σ = 36
Variance = σ2 = 362 = 1296.
Question 65.
Which one of the following is not a Central Tendency? [1 Mark, Nov. 2018]
(a) Mean Deviation
(b) Arithmetic mean
(c) Median
(d) Mode
Solution:
(a)
![]()
Question 66.
If the range of a set of values is 65 and maximum value in the set is 83, then the minimum value in the set is ________. [1 Mark, Nov. 2018]
(a) 74
(b) 9
(c) 18
(d) None of the above
Solution:
(c)
Range = L – S
65 = 83 – S
∴ S = 83 – 65 =18
Question 67.
If σ2 = 100 and coefficient of variation = 20% then \(\overline{\mathrm{X}}\) = ________. [1 Mark, June 2019]
(a) 60
(b) 70
(c) 80
(d) 50
Solution:
(a)
If σ2 = 100, So σ = \(\sqrt{100}\) = 10
C.V. = \(\frac{\text { S.D }}{\text { A.M }}\) × 100
20 = \(\frac{10}{\overline{X}}\) × 100
20\(\overline{\mathrm{X}}\) = 1000 ; \(\overline{\mathrm{X}}\) = 50
![]()
Question 68.
If the points of inflexion of a Normal Curve are 40 and 60 respectively, then its mean deviation is _______. [1 Mark, June 2019]
(a) 8
(b) 45
(c) 50
(d) 60
Solution:
(a)
If the point of inflexion of a Normal Distribution are 40 and 60.
Formula, μ – σ = 40 …………….. (1)
μ + σ = 60 …………… (2)
Solving eqns. (1) and (2); we get
μ = 50, σ = 10
Then M.D. = 0.8. σ = 0.8 × 10 = 8
Question 69.
Standard deviation is __________ times of \(\sqrt{\mathrm{MD} \times \mathrm{QD}}\) [1 Mark, June 2019]
(a) 2/3
(b) 4/5
(c) \(\sqrt{\frac{15}{8}}\)
(d) \(\sqrt{\frac{8}{15}}\)
Solution:
(c)
We know that,
4 S.D = 5 M.D = 6 Q.D
Let, 4 S.D =5 M.D = 6 Q.D = LCM of 4, 5, 6 = 60
S.D = 60/4= 15
MD = 60/5 = 12
QD = 60/6 = 10
Let SD is x times of \(\sqrt{\mathrm{MD} \times \mathrm{QD}}\)
SD = x \(\sqrt{\mathrm{MD} \times \mathrm{QD}}\)
15 = x \(\sqrt{12 \times 10}\)
Squaring on both sides ; we get
225 = x2 . 12 × 10
So x = \(\sqrt{\frac{225}{12 \times 10}}\) = \(\sqrt{\frac{15}{8}}\)
![]()
Question 70.
The Q.D of 6 numbers 15, 8, 36, 40, 38,41 is equal to _________. [1 Mark, June 2019]
(a) 12.5
(b) 25
(c) 13.5
(d) 37
Solution:
(c) Arranging cbs. in Ascending order, we get
8, 15, 36, 38, 40, 41
Here, N = 6
Q1 = \(\left(\frac{\mathrm{N}+1}{4}\right)^{\mathrm{th}}\) term
= \(\left(\frac{6+1}{4}\right)^{\text {th }}\) term = 1.75th term
= 1st term + 0.75 (2nd term – 1st term)
= 8 + 0.75 × (15 – 8)
= 8 + 0.75 × 7
= 8 + 5.25
= 13.25
Q3 = 3\(\left(\frac{\mathrm{N}+1}{4}\right)^{\mathrm{th}}\)obs.
= \(\frac{3(6+1)^{\text {th }}}{4}\) term = 5.25th term
= 40 + 0.25 (41 – 40)
= 40 + 0.25 × 1
= 40 + 0.25 = 40.25
QD = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}\)
= \(\frac{40.25-13.25}{2}\) = \(\frac{27}{2}\) = 13.5
![]()
Question 71.
S.D of first five consecutive natural numbers is ________. [1 Mark, June 2019]
(a) \(\sqrt{10}\)
(b) \(\sqrt{8}\)
(c) \(\sqrt{3}\)
(d) \(\sqrt{2}\)
Solution:
(d)
S.D of 1st ‘n’ Natural No. = \(\sqrt{\frac{n^2-1}{12}}\)
n = 5
S.D = \(\sqrt{\frac{5^2-1}{12}}\) = \(\sqrt{\frac{5^2-1}{12}}\) = \(\sqrt{2}\)
Question 72.
If the profit of a company remain same for the last ten months then the S.D. of profits of the company would be : [1 Mark, June 2019]
(a) Positive
(b) Negative
(c) Zero
(d) (a) or (c)
Solution:
(c)
If the profits of a company remain same for ten months, then S.D = 0
(Since shifting of origin S.D is not changed)
![]()
Question 73.
Coefficient of quartile deviation is 1/4 then Q3/Q1 is _________. [1 Mark, June 2019]
(a) 5/3
(b) 4/3
(c) 3/4
(d) 3/5
Solution:
(a)
Coeff. of Q.D = \(\frac{1}{4}\)
\(\frac{1}{2}\) = \(\frac{1}{4}\) [cross product]
or; 4 Q3 – 4Q1 = Q3 + Q1
or; 4 Q3 – Q3 = Q1 + 4Q1
or; 3 Q3 = 5 Q1
or; \(\frac{\mathrm{Q}_3}{\mathrm{Q}_1}\) = \(\frac{5}{3}\)
![]()
Question 74.
The sum of mean and SD of a series is a + b, if we add 2 to each observation of the series then the sum of mean and SD is ________. [1 Mark, June 2019]
(a) a + b + 2
(b) 6 – a + b
(c) 4 + a – b
(d) a + b + 4
Solution:
(a) If a constant quantity is added to each observation, then value of mean changes but SD remains unchanged.
Since, Mean + S.D = (a + b)
If we add ‘2’ in each observation , then new (mean + S.D) = (a + b + 2)