Investment Decisions – CA Inter FM Question Bank is designed strictly as per the latest syllabus and exam pattern.
Investment Decisions – CA Inter FM Question Bank
Question 1.
Beta Company Limited is considering replacement of its existing machine by a new machine, which ¡s expected to cost ₹ 2,64,000. The new machine will have a life of five years and will yield annual cash revenues of ₹ 5,68,750 and incùr annual cash expenses of ₹ 2,95,750. The estimated salvage value of the new machine is ₹ 18,200. The existing machine has a book value of ₹ 91,000 and can be sold for ₹ 45,500 today.
The existing machine has a remaining useful life of five years. The cash revenues will be ₹ 4,55,000 and associated cash expenses will be ₹ 3,18,500. The existing machine will have a salvage value of ₹ 4,550, at the end of five years. The Beta Company is in 35% tax bracket, and writes off depreciation at 25% on the written-down value method.
The Beta Company has a target debt-to-value ratio of 15%. The Company in the past has raised debt at 11 % and it can raise fresh debt at 10.5%. Beta Company plans to follow dividend discount model to estimate the cost of equity capital. The Company plans to pay a dividend of ₹ 2 per share in the next year. The current market price of Company’s equity share is ₹ 20 per equity share. The dividend per equity share of the Company is expected to grow at 8% p.a.
Required:
(i) Compute the incremental cash flows of the replacement decision.
(ii) Compute the weighted average cost of Capital of the Company.
(iii) Find out the net present value of the replacement decision.
(iv) Estimate the discounted payback period of the replacement decision.
(v) Should the Company replace the existing machine? Advise. (Nov 2003, 5+3+2+1+1 = 12 marks)
Answer:
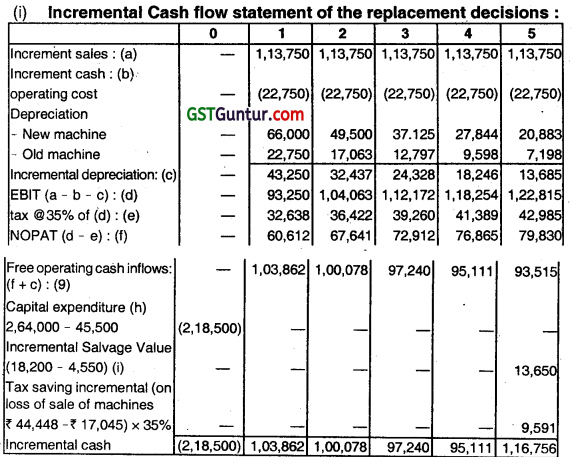
Flows of the replacement decision:
(ii) Computation of WACC of the Co.:
Ke = \(\frac{D_1}{P_0}+g\) = \(\frac{₹ 2}{₹ 20}\) + 8 % =18%
Kd = 10.5% (1 – 0.35) = 6.825%
WACC = Kd × \(\frac{D}{D+E}\) + Ke × \(\frac{E}{E+D}\)
= (6.825% × 15%) + (18% × 85%)
= 16.32% or 16.32375%
(iii) Computation of Net Present Value of the replacement decision:
NPV = \(\sum_{t=1}^5 \frac{\text { FCFFt }}{(1+0.1632375)^t}-01 \)
= (2,18,500) + 89,287 + 73,961 + 61,779 + 51,948 + 54,820 = ₹ 1,13,295/-
(iv) Discounted payback period of the replacement decision:
= 2 years + 10 months 22 days approx.
(v) Advise:
The company should replace the existing machine with new machine.
Question 2.
XYZ Ltd. is planning to introduce a new product with a project life of 8 years The project is to be setup in Special Economic Zone (SEZ) and qualifies for one one-time (at starting) tax-free subsidy from the State Government of ₹ 25,00,000 on Capital investment. The initial equipment cost will be ₹ 1.75 crores. Additional equipment cost ₹ 12,50,000 will be purchased at the end of the third year from the cash inflow of this year. At the end of 8 years, the original equipment will have no resale value, but additional equipment can be sold for ₹ 1,25,000. A Working Capital of ₹ 20,00,000 will be needed and it will be released at the end of eighth year. The project will be financed with a sufficient amount of Equity Capital. The sales volumes over eight years have been estimated as follows:
| Year | 1 | 2 | 3 | 4-5 | 6-8 |
| Units | 72,000 | 1,08,000 | 2,60,000 | 2,70,000 | 1,80,000 |
A sales price of ₹ 120 per unit is expected and variable expenses will amount to 60% of sales revenue. Fixed Cash operating costs will amount ₹18,00,000 per year. The loss of any year will be set off from the profits of subsequent two years. The company is subject to 30% tax rate and considers 12 percent to be an appropriate after-tax cost of Capital for this project. The company follows straight line method of depreciation.
Required:
Calculate the net present value of the project and advise the management to take appropriate decision
Note:
The PV factors at 12% are
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 8.893 | .797 | .712 | .636 | .567 | .507 | .452 | .404 |
(Nov 2007, 8 marks)
Answer:
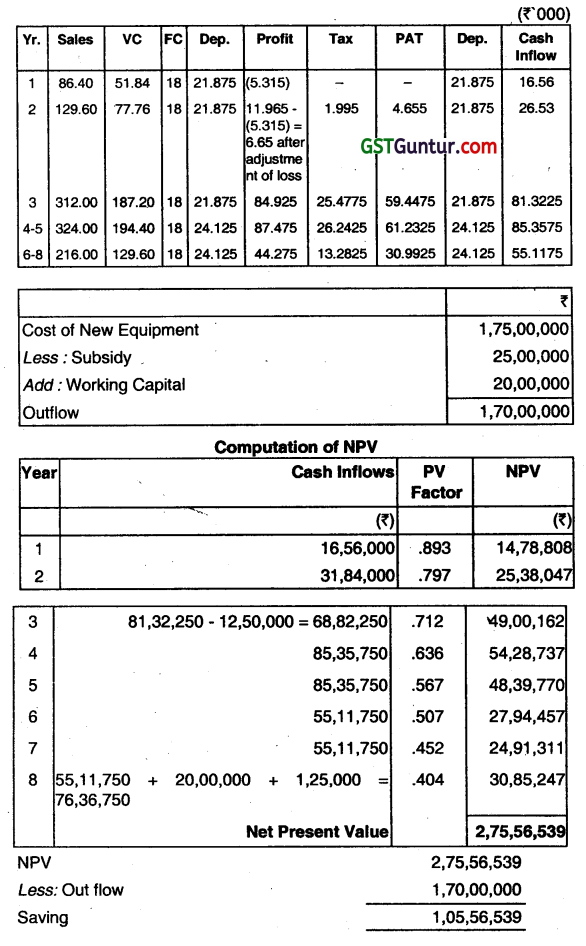
Advise: Since the project has a positive NPV, therefore, it should be accepted.
![]()
Question 3.
A company wants to invest in a machinery that would cost ₹ 50,000 at the beginning of year 1. It is estimated that the net cash inflows from operations will be ₹ 18,000 per annum for 3 years if the company opts to service a part of the machine at the end of year 1 at ₹ 10,000 and the scrap value at the end of year 3 will be ₹ 12,500. However, if the company decides not to services the part, ¡t will have to be replaced at the end of year 2 at ₹ 15,400. But in this case, the machine will work for the 4th year also and get operational cash inflow of ₹ 18,000 for the 4th year. It will have to be scrapped at the end of year 4 at ₹ 9,000. Assuming cost of capital at 10% and ignoring taxes, will you recommend the purchase of this machine based on the net present value of Its cash flows?
If the supplier gives a discount of ₹ 5,000 for purchase, what would be your decision? (The present value factors at the end of years 0, 1, 2, 3, 4, 5, and 6 are respectively 1, 0.9091, 0.8264, 0.7513, 0.6830, 0.6209 and 0.5644). (Nov 2008, 7 marks)
Answer:
Option 1: Purchase Machinery and Service Part at the end of Year 1
Net Present value of cash flow @ 10% per annum discount rate.
NPV= \( -50,000+\frac{18,000}{(1.1)}+\frac{18,000}{(1.1)^2}+\frac{18,000}{(1.1)^3}-\frac{10,000}{(1.1)}+\frac{12,500}{(1.1)^3}\)
= – 50,000 + 18,000 (0.9091 + 0.8264 + 0.7513) – (10,000 × 0.9091 + 12,500 × 0.751 3)
= 50,000 + (18,000 x 2.4868) – 9,091 + 9,391
= – 50,000+44,762 – 9,091 + 9,391
NPV=- 4,938
Since, Net Present Value is negative, therefore, this option is not to be considered.
If Supplier gives a discount of ₹ 5,000 then,
NPV=+ 5,000 – 4,938 = + 62
In this case, Net Present Value is positive but very small, therefore, this option may not be advisable.
Option II: Purchase Machinery and Replace Part at the end of Year 2.
NPV = \(-50,000+\frac{18,000}{(1.1)}+\frac{18,000}{(1.1)^2}+\frac{18,000}{(1.1)^3}-\frac{15,400}{(1.1)^2}+\frac{27,000}{(1.1)^4}\)
= – 50,000 + 18,000(0.9091 + 0.8264 + 0.7513) – (15,400 × 0.8264) + (27,000 × 0.6830)
= – 50,000 + 18,000 (2.4868) – (15,400 × 0.8264) + (27,000 × 0.6830)
= – 50,000 + 44,762 – 12,727 +18,441
= – 62,727 + 63,203
= + 476
Net Present Value is positive, but very low as compared to the investment.
If the Supplier gives a discount of ₹ 5,000 then
NPV = 5,000 + 476 = 5,476
Decision: Option II is worth investing as the net present value is positive and higher as compared to Option I.
Question 4.
PD Ltd. an existing company, is planning to introduce a new product with projected life of 8 years. Project cost will be ₹ 2,40,00,000. At the end of 8 years no residual value will be realized. Working capital of ₹ 30,00,000 will be needed. The 100% capacity of the project is ₹ 2,00,000 units p.a. but the Production and Sales Volume is expected are as under:
| Year | Number of Units |
| 1 | 60,000 units |
| 2 | 80,000 units |
| 3-5 | 1,40,000 units |
| 6-8 | 1,20,000 units. |
Other Information:
(i) Selling price per unit ₹ 200.
(ii) Variable cost is 40% of sales.
(iii) Fixed cost p.a. ₹ 30,00,000.
(iv) In addition to these advertisement expenditures will have to be incurred as under:
| Year | 1 | 2 | 3-5 | 6-8 |
| Expenditure (₹) | 50,00,000 | 25,00,000 | 10,00,000 | 5,00,000 |
(v) Income Tax is 25%.
(vi) Straight line method of depreciation is permissible for tax purposes.
(vii) Cost of capital is 10%.

Advise about the project acceptability. (Nov 2018, 10 marks)
Answer:

Advice: Since the project has a positive NPV, therefore it should be accepted.
Question 5.
Door Ltd. is considering an investment of ₹ 4,00,000. This investment is expected to generate substantial cash inflows over the next five years. Unfortunately, the annual cash flows from this investment is uncertain, but the following probability distribution has been established.
| Annual Cash Flow (₹) | Probability |
| 50,000 | 0.3 |
| 1,00,000 | 0.3 |
| 1,50,000 | 0.4 |
At the end of its 5 years life, the investment is expected to have a residual value of 40,000.
The cost of capital is 5%.
(i) Calculate NPV under the three different scenarios.
(ii) Calculate Expected Net Present Value
(iii) Advise Door Ltd. on whether the investment is to be undertaken.
| Year | 1 | 2 | 3 | 4 | 5 |
| DF @ 5% | 0.952 | 0.907 | 0.864 | 0.823 | 0.784 |
(Nov 2019, 5 Marks)
Answer:
(i) NPV under the three different scenarios:
(a) When Probability is 0.3
NPV = Annual cash flow (PVAf, 5%,5) + Residual value (Pvif 5%,5) – Initial Investment
= (₹ 50,000 × 4.33) + (₹ 40,000 × 0.784) – 4,00,000
= ₹ 2,16,500 + ₹ 31,360 – ₹ 4,00,000
NPV = – ₹ 1,52,140
(b) When Probability is 0.3
NPV = (₹ 1,00,000 × 4.33) + (₹ 40,000 × 0.784) – ₹ 4,00,000
= ₹ 4,33,000 + ₹ 31,360 – ₹ 4,00,000
NPV = ₹ 64,360
(c) When Probability Is 0.4
NPV = (₹ 1,50,000 × 4.33) + (₹ 40,000 × 0.784) – ₹ 4,00,000
= ₹ 6,49,500 + ₹ 31,360 – ₹4,00000
NPV = ₹ 2,80,860
(ii) Expected Net Present Value:
Annual Expected cash flows
= (₹ 50,000 × 0.3) + (₹ 1,00,000 × 0.3) + (₹ 1,50,000 × 0.4)
= ₹ 1,05,000
NPV = (₹ 1,05,000 × 4.33) + (₹ 40,000 × 0.784) – ₹ 4,00,000
= ₹ 4,54,650 + ₹ 31,360 – ₹ 4,00,000
NPV = ₹ 86,010
(iii) Since the expected NPV from the investment is positive (₹ 86,010), Door Ltd. should undertake the project.
Question 6.
CK Ltd. is planning to buy a new machine. Details of which are as follows:
Cost of the Machine at the commencement ₹ 2,50,000
Economic Life of the Machine 8-year
Residual Value Nil
Annual Production Capacity of the Machine 1,00,000 units
Estimated Selling Price per unit. ₹ 6
Estimated Variable Cost per unit ₹ 3
Estimated Annual Fixed Cost ₹ 1,00,000
(Excluding depreciation)
Advertisement Expenses in year in addition of annual fixed cost ₹ 20,000
Maintenance Expenses in 5th year in addition of annual fixed cost ₹ 30,000
Cost of Capital 1 2%
Ignore Tax.
Analyse the above-mentioned proposal using the Net Present Value Method and advice.
P.V. factor @ 12% are as under:
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| PV Factor | 0.893 | 0.797 | 0.712 | 0.636 | 0.567 | 0.507 | 0.452 | 0.404 |
(Nov 2020, 5 marks)
Question 7.
Desirability factor. (Nov 2009, 1.5 marks)
Answer:
In certain cases, we have to compare a number of proposals each involving different amount of cash inflows. One of the methods of comparing such proposals is to work out, what is known as the ‘Desirability Factor’ or ‘Profitability Index’. In general terms, a project is acceptable if the Profitability Index is greater than 1. Mathematically, Desirability Factor = \(\frac{\text { Sum of Discounted Cash inflows }}{\text { Initial Cash Outlay or Total Discounted Cash outflows }} \)
![]()
Question 8.
Distinguish Between:
Net Present-value and Internal Rate of Return. (May 2002, 2 marks)
OR
Net present value method and internal rate of return method. (Nov 2011, 4 marks)
OR
Net Present Value (NPV) and Internal Rate of Return (IRR) methods for evaluating projects. (2015 Nov, 4 marks)
Answer:
Difference between NPV and IRR
| Basis of Difference | NPV | IRR |
| 1. Nature of Projects accepted | Under NPV, projects with positive NPV are accepted. | Under IRR, projects whose IRR is more than the cost of project are accepted. |
| 2. Measures | NPV measures both quality and scale of investment. | IRR measures only quality of investment. |
| 3. Absolute Vs Relative Measure | NPV provides an absolute measure in quantitative terms. | IRR Provides a relative measure In percentage. |
| 4. ReInvestment Rate | Under NPV, cash flows are re-invested at the rate of cost of capital. | Under IRR, cash flows are re-invested at the rate of IRR |
| 5. Multiple/Negative Rate | NPV cannot yield Multiple or Negative Rate | IRR can yield negative or multiple rate under certain circumstances. |
Question 9.
A Company proposes to install a machine involving a Capital Cost of ₹ 3,60,000. The life of the machine is 5 years and its salvage value at the end of the life is nil. The machine will produce the net operating income after depreciation of ₹ 68,000 per annum. The Company4s tax rate is 45%.
The Net Present Value factors for 5 years are as under:
Discounting Rate: 14 15 16 17 18
Cumulative factor: 3.43 3.35 3.27 3.20 3.13
You are required to calculate the internal rate of return of the proposal. (Nov 2002, 4 marks)
Answer:

The IRR of the investment can be found as follows:
NPV =₹ 3,60,000 +₹ 1,09,400 (PVIFA5.r) = O
PVIFA5.r (Cumulative factor) = \(\frac{₹ 3,60,000}{₹ 1,09,400}\) = 3.29

IRR = 15+ \(\left(\frac{6,490}{6,490+2,262}\right)\)
= 15 + 0.74 = 15.74%
Question 10.
What is the ‘Internal Rate of Return’? Explain. (Nov 2014, 4 marks)
Answer:
Internal Rate of Return:
It is that rate at which discounted cash inflows are equal to the discounted cash outflows.
It can be stated in the form of a ratio as follows:
\(\frac{\text { Cash inflows }}{\text { Cash Outflows }}\) = 1
This rate is to be found by trial and error method.
This rate is used in the evaluation of investment proposals. In this method, the discount rate is not known but the cash outflows and cash inflows are known. In evaluating investment proposals, internal rate of return is compared with a required rate of return, known as cut-off rate. If it is more than cut-off rate the project is treated as acceptable; otherwise project is rejected.
Question 11.
Define Internal Rate of Return (IRR) (Jan 2021, 4 marks)
Question 12.
Explain the concept of discounted payback period. (May 2009, 3 marks)
Answer:
Concept of Discounted Payback Period
Payback period is time taken to recover the original investment from project cash flows. It is also termed as break-even period. The focus of the analysis is on liquidity aspect and it suffers from the limitation of ignoring time value of money and profitability.
Discounted payback period considers present value of cash flows, discounted at company’s cost of capital to estimate breakeven period i.e. it is that period in which future discounted cash flows equal the initial outflow.
The shorter the period, better it is. It also ignores post-discounted payback period cash flows. it takes care of the time value of money.
![]()
Question 13.
Explain the concept of Multiple Internal rate of Return (MIRR). (Nov 2008, 3 marks)
Answer:
Concept of MIRR
MIRR is that rate of compounding which makes the initial cash outflow ¡n zeroth year equal to the terminal value of cash inflows. In order to cope up various limitations of the conventional Internal Rate of Return, Modified Internal Rate of Return was developed. Under this method, all cash flows (except initial investment), are brought to the terminal value using an appropriate discount rate (generally the cost of capital). MIRR results in a single stream of cash inflow in the terminal year. It is obtained by assuming a single outflow in the zero the year and the terminal cash inflow. The discount rate which equates the PV of the terminal cash inflow to the zeroth year outflow is known as MIRR.
Some of the advantages of MIRR are
- This method makes use of concept of time value of money.
- All the Cash flows in the project are considered.
Some of the limitations of MIRR are
- The calculation process is tedious.
- The IRR approach creates a peculiar situation if we compare two projects with different inflow-outflow patterns.
- In case of mutually exclusive projects decisions based only on IRR may not be correct.
Question 14.
Define Modified Internal Rate of Return method. (May 2007, 2 marks)
Answer:
In order to cope up various limitations of the conventional internal Rate of Return, Modified Internal Rate of Return was developed.
Limitations of the conventional IRR are,
- it eliminates multiple IRR rates.
- it addresses to reinvestment rate issue and produces results, which are consistent with the Net Present Value (NPV) method.
Under this method, all cash flows (except initial investment), are brought to the terminal value using an appropriate discount rate (generally the cost of capital). MIRR results in a single stream of cash inflow in the terminal year. It is obtained by assuming a single outflow in the zeroth year and the terminal cash inflow. The discount rate which equates the PV of the terminal cash Inflow to the zeroth year outflow is known as MIRR.
Question 15.
The cash flows of projects C and D are reproduced below:

(i) Why there is a conflict of rankings?
(ii) Why should you recommend Project C in spite of lower internal rate of return?
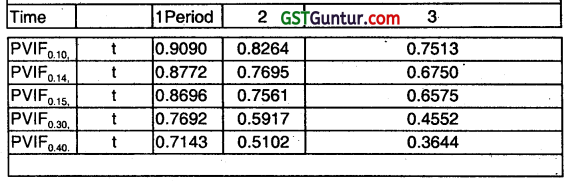
(May 2003, 4+4 = 8 marks)
Answer:
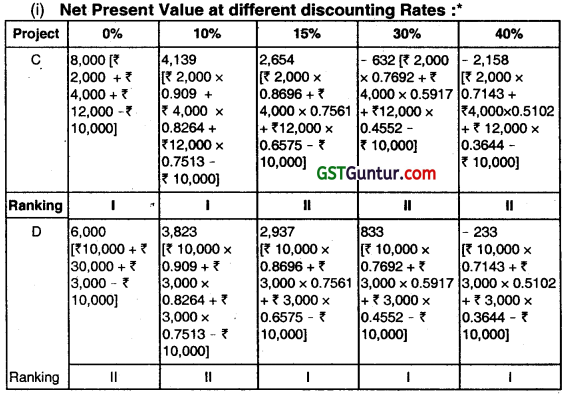
The conflict in ranking arises because of skewness in cash flows, In the case of Project C, Cash flows occurs more late in the life but in the case of Project D, cash flows are skewed towards the beginning.
At lower discount rate, Project C’s NPV will be higher than that of Project D’s. As the discount rate increases, Projects C’s NPV will fall at a faster rate, due to the compounding effect.
After break-even discount rate, Project D has higher NPV as well as higher IRF.
(ii) If the opportunity cost of funds is 10%, Project C should be accepted because the firm’s wealth will increase by ₹ 316 (₹ 4.139 – ₹ 3,823):
The following statement of Incremental analysis will prove the above point:
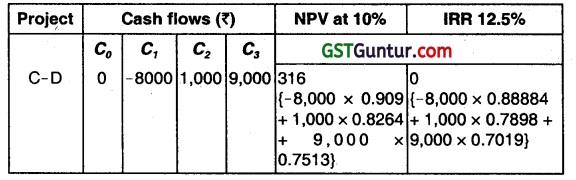
Hence, the Project C should be accepted, when the opportunity cost of funds is 10%.
Question 16.
The cash flows of two mutually exclusive Projects are as under:

Required:
(i) Estimate the net present value (NPV) of the Project P’ and J’
using 15% as the hurdle rate.
(ii) Estimate the internal rate of return (IRR) of the Project ‘P’ and ‘J’.
(iii) Why there is a conflict in the project choice by using NPV and IRR criterion?
(iv) Which criteria you will use in such a situation? Estimate the value at that criterion. Make a project choice.
The present value interest factor values at different rates of discount are as under:
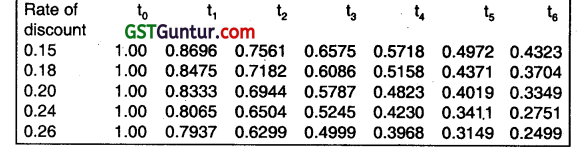
(May 2004, 2+2+ 1 +2 = 7 marks)
Answer:
(i) Estimation of NPV of the Project ‘P’ & J using 15% as the hurdle rate:
NPV of Project ‘P’:
= – 40,000 + \(\frac{13,000}{(1+15)^1}+\frac{8,000}{(1.15)^2}+\frac{14,000}{(1.15)^3}+\frac{12,000}{(1.15)^4}+\frac{11,000}{(1.15)^5}+\frac{15,000}{(1.15)^6}\)
= – 40,000 + 11.304.35 + 6049.15+ 9205.68+6861.45 + 5469.37 + 6485.65
= ₹ 5375.65
= ₹ 5376/-
NPV of Project J:
=-20,000 + \(\frac{7,000}{(1.15)^1}+\frac{13,000}{(1+15)^2}+\frac{12,000}{(1+15)^3} \)
= -20,000 + 6086.96 + 9829.87 + 7890.58
= ₹ 3807.41
(ii) Estimation of IRR of Project ‘P’ & ‘J’: IRR is the rate at which the sum of cash mf lows after discounting equals to the discounted cash outflows. The value of ‘r1 in the case of given projects can be determined by using the following formula:
Co = \(\frac{C F_0}{(1+r)^0}+\frac{C_1}{(1+r)^1}+\ldots \ldots \ldots \ldots \ldots \ldots+\cdots+\frac{C F_n}{(1+r)^n}+\frac{S V+W C}{(1+r)^n}\)
Where, C0 = Cash flows at the time 0
CF1 = Cash inflow at the end of years t.
r = discount rate
n = life of the project
SV & WC = Salvage value & working capital at end of ‘n’ years.
IRR of Project ‘P’:
40,000 = \(\frac{13,000}{(1+r \%)^1}+\frac{8,000}{(1+r \%)^2}+\frac{14,000}{(1+r \%)^3}+\frac{12,000}{(1+r \%)^4}+\frac{11,000}{(1+r \%)^5}+\frac{15,000}{(1+r \%)^6} \)
r = 19.73%
IRR of Project ‘J’:
20000 = \(\frac{7,000}{(1+r \%)^1}+\frac{13,000}{(1+r \%)^2}+\frac{12,000}{(1+r \%)^3} \)
r = 25.20%
(iii) The conflict between NPV & IRR rule in the case of mutually exclusive projects situation arises due to re-investment rate assumptions. NPV rule assumes that intermediate cash flows are reinvested at ‘r’. The assumption of NPV rules is more realistic.
(iv) When there is a conflict in the Project choice by using NPV & IRR criterion, we would prefer to Equal Annualised Criterion’. According to this, the net annual each inflow in the case of Project P & J would be:
= \(\frac{\text { Net Present Value }}{\text { Cumulative P.V. of Re 1 pa@ } 15 \% \text { for } 6 \text { Years }} \)
Project P’ = ₹ 5375.65/3.7845 = ₹ 1,420.44
Project ‘J’ = ₹ 3807.41/2.2832 = ₹ 1,667.58
Since the cash inflow p.a. in case of project ‘J’ is more than that of project ‘P’, so Project ‘J’ is recommended.
![]()
Question 17.
MNP Limited is thinking of replacing its existing machine by a new machine, which would cost ₹ 60 lakhs. The company’s current production is 80,000 units, and is expected to Increase to 1,00,000 units, if the new machine ¡s bought. The selling price of the product would remain unchanged at ₹ 200 per unit. The following is the cost of producing one unit of product using both the existing and new machine:
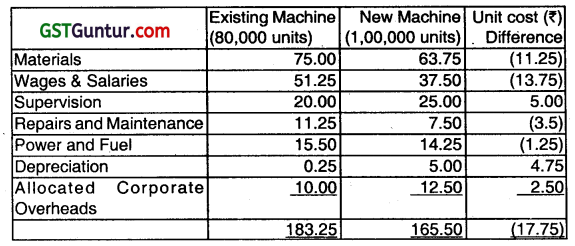
The existing machine has an accounting book value of ₹ 1,00,000 and it has been fully depreciated for tax purpose. It is estimated that machine will be useful for 5 years. The supplier of the new machine has offered to accept the old machine for ₹ 2,50,000. However, the market price of old machine today is ₹ 1,50,000 and it is expected to be ₹ 35,000 after 5 year. The new machine has a life of 5 years and a salvage value of ₹ 2,50,000 at the end of its economic life. Assume corporate Income-tax rate at 40% and depreciation is charged on straight-line basis for Income-tax purposes. Further, assume that book profit is treated as ordinary income for tax purposes. The opportunity cost of capital of the Company is 15%.
Required:
(i) Estimate net present value of the replacement decision.
(ii) Estimate the internal rate of return of the replacement decision.
(iii) Should Company go ahead with the replacement decision? Suggest.

(Nov 2005, 8+3+ 1 =12 marks)
Answer:
(i) Net Cash Outlay of New Machine:-

Market Value of Old Machine: The old machine could be sold for ₹ 1,50,000 in the market. Since the exchange value Is more than the market value, this option is not attractive. This opportunity will be lost whether the old machine is retained or replaced. Thus, on incremental basis, it has no impact.
Depreciation base: Old machine has been fully depreciated for tax purpose. Thus, the depreciation base of the new machine will be its original cost, i.e. ₹ 60,00,000.
Net Cash Flows: Unit cost includes depreciation & allocated overheads. Allocated OHs are allocations from corporate office therefore they are irrelevant. The depreciation tax shield may be computed separately. Excluding depreciation and allocated OHs, unit costs can be calculated. The company will obtain additional revenue from additional 20,000 units sold.
Thus, after-tax saving, excluding depreciation, tax shield, would be,
= (1,00,000 (200 – 148) -80,000 (200 – 173)) × (1 – 0.40)
= (52,00,000 -21,60,000) × 0.60
= 18,24,000.
After adjusting depreciation, tax should and salvage value, net cash flows and net present value is estimated.
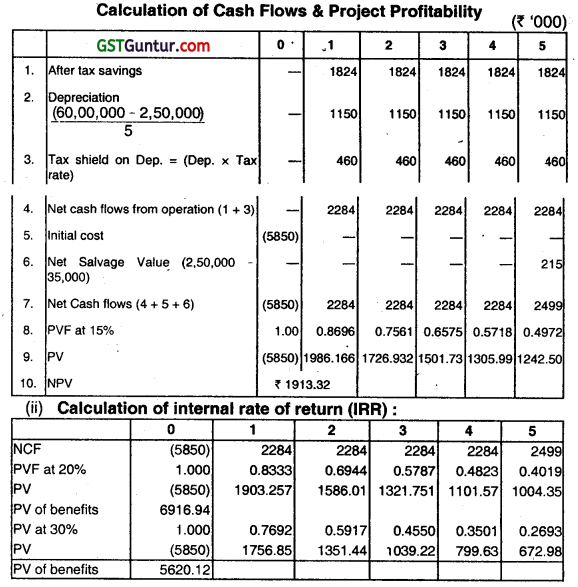
IRR = 20% + 10% × \(\frac{1066.94}{1296.82}\) = 28.23%
(iii) Advise: The company should go ahead with replacement project since it is positive NPV decision.
Question 18.
Explain the steps while using the equivalent annualized criterion. (Nov 2019, 3 marks)
Answer:
Equivalent Annualised Criterion involves the following steps:
1. Compute NPV using the WACC or discounting rate
2. Compute present value Annuity Factor (PVAF) of discounting factor used above for the period of each project.
3. Divide NPV computed under step
- by PVAF as compute under step
- and compare the values.
Question 19.
A company has to make a choice between two projects namely A and B. The initial capital outlay of two Projects are ₹ 1,35,000 and ₹ 2,40,000 respectively for A and B. There will be no scrap value at the end of the life of both the projects. The opportunity Cost of Capital of the company is
16%. The annual incomes are as under:
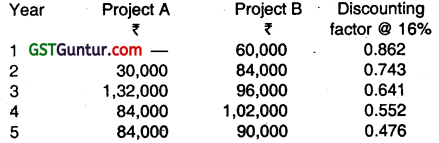
You are required to calculate for each project:
(i) Discounted payback period
(ii) Profitability index
(iii) Net present value. (Nov 2002, 6 marks)
Answer:
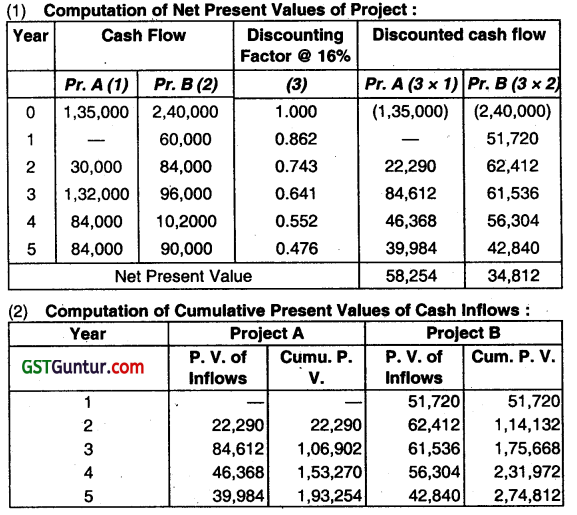
(i) Discounted Payback Period (Refer W. N.-2):
Cost of Project A = ₹ 1,35,000
Cost of Project B = ₹ 2,40,000
Cumulative of PV of cash inflows of Project
A after 4 yrs. = ₹ 1,53,270
Cumulative PV of cash ¡nf lows of Project
B after 5 years = ₹ 2,74,812
A comparison of projects cost with this cumulative PV clearly shows that the Project As cost will be recovered in less than 4 years & that of Project B in less than 5 years. The exact duration of discounted payback period can be computed as follows.

(ii) Profitability Index (P.I.) = \(\frac{\text { Sum of discount cash Inflow }}{\text { Initial cash outlay }} \)
P.I. (Pr.A)= \(\frac{₹ 1,93,254}{₹ 1,35,000}\) = 1.43
P.I. (Pr. B) = \(\frac{₹ 2,74,812}{₹ 2,40,000} \) = 1.15
(iii) Net Present Value:
Pr. A (W.N.-1) = ₹ 58,254
Pr. B(W.N.-1)= ₹ 34,812
Question 20.
A Company is considering a proposal of installing a drying equipment. The equipment would involve a Cash outlay of ₹ 6,00,000 and net Working Capital of ₹ 80,000. The expected lite of the project is 5 years without any salvage value. Assume that the company is allowed to charge depreciation on straight-line basis for Income-tax purpose. The estimated before-tax
cash inflows are given below:

The applicable Income-tax rate to the Company is 35%. If the Company’s opportunity Cost of Capital is 12%, calculate the equipment’s discounted payback period, payback period, net present value and internal rate of return.

(May 2006, 10 Marks)
Answer:
Initial outlay = 6,00,000 + 80,000 = 6,80,000
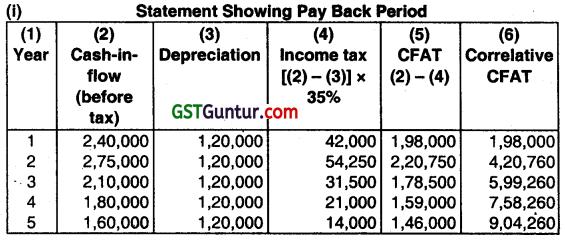
Payback period = 3 + \(\frac{80,740}{7,58,260-5,99,260} \)
=3+51 =3.51 year.
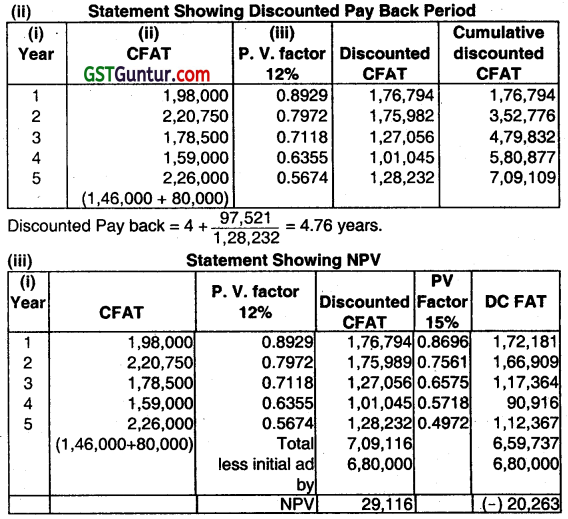
NPV = 7,09,116 – 6,80,000 = 29,116
IRR = 12% + \(\frac{29,116}{29,116+20,364} \times 3 \%\)
= 12% + \(\frac{29,116}{49,480} \times 3 \%\) =12% + 1.77% = 13.77%
![]()
Question 21.
C Ltd. is considering investing in a project. The expected original investment in the project will be ₹ 2,00,000, the life of project will be 5 years with no salvage value. The expected net cash inflows after depreciation but before tax during the life of the project will be as following:
| Year | 1 | 2 | 3 | 4 | 5 |
| ₹ | 85,000 | 100,000 | 80,000 | 80,000 | 40,000 |
The project will be depreciated at the rate of 20% on original cost. The company is subjected to 30% tax rate.
Required:
(i) Calculate payback period and average rate of return (ARR).
(ii) Calculate net present value and net present value index, It cost of capital is 10%.
(iii) Calculate internal rate of return.
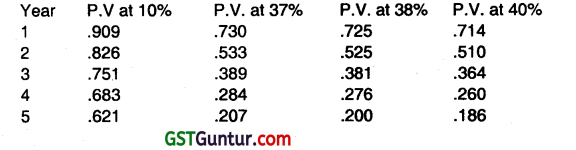
(May 2008, 2 + 3 +3 = 8 marks)
Answer:
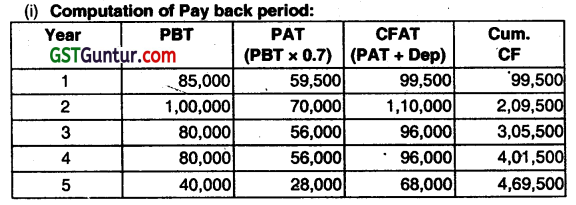
Depreciation = 2,00,000 × 20% = 40,000
Payback period = 1+ (2,00000 – 99,500)/1,10,000 =1.91 years
Computation of Average Rate of Return:
| Year | PBT | PAT (PBT × 0.7) |
| 1 | 85,000 | 59,500 |
| 2 | 1,00,000 | 70,000 |
| 3 | 80,000 | 56,000 |
| 4 | 80,000 | 56,000 |
| 5 | 40,000 | 28,000 |
| Total | 2,69,500 |
Average Annual Profit =2,69,500/5 = 53,900
Average Investment = (2,00,000 +0)/2 = 1,00,000
ARR = \(\frac{\text { Average Annual Profit after tax }}{\text { Average Investment }} \)
ARR = 53,900 ÷ 1,00,000 = 0.539 i.e. 53.9%.
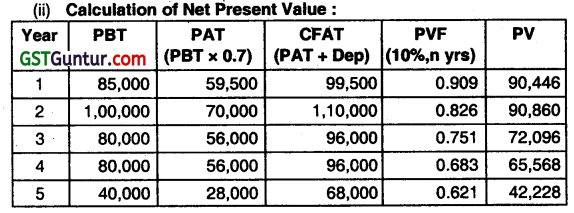

NPV is positive hence C Ltd. can accept the proposal.
NPV Index (PI):
NPV = 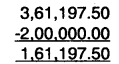
NPV Index = \(\frac{1,61,197.50}{2,00,000}\) = 0.81

Calculation of IRR through Interpolation method
IRR= LR + \(\frac{N P V_L}{N P V_L-N P V_H} \times \text { (Rate difference) }\)
IRR=37%+ \(\frac{9,949}{9949-(-305)} \times(40 \%-37 \%)\)
= 37% + \(\frac{9,949}{10,254} \times 3 \%\)
= 37% + 2.91%
IRR = 39.91%
Question 22.
The management of P Limited is considering to select a machine out of the two mutually exclusive machines. The company’s cost of capital is 12 percent and corporate tax rate for the company is 30 percent. Details of the machines are as follows:
| Machine-I | Machine-II | |
| Cost of machine | ₹ 10,00,000 | ₹ 15,00,000 |
| Expected life | 5 years | 6 years |
| Annual income before tax and depreciation | ₹ 3,45,000 | ₹ 4,55,000 |
Depreciation is to be charged on a straight-line basis.
You are required to:
(i) Calculate the discounted pay-back period, net present value, and internal rate of return for each machine.
(ii) Advise the management of P Limited as to which machine they should take up.

(May 2010, 9 Marks)
Answer:
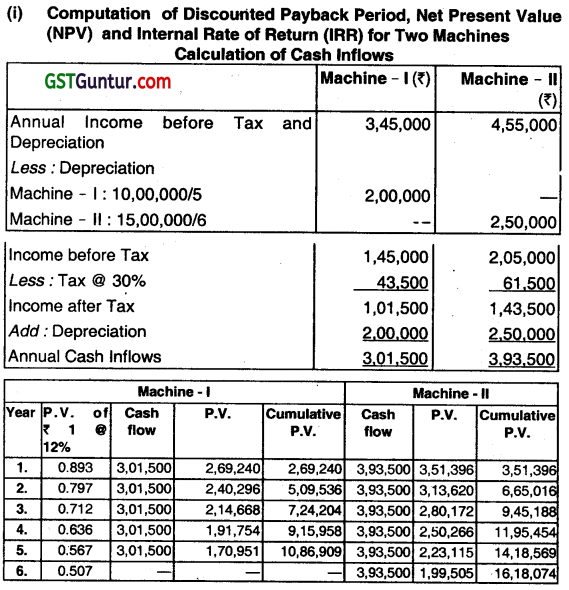
Discounted Payback Period for:
Machine-I
Discounted Payback Period = 4 + \(\frac{(10,00,000-9,15,958)}{1,70,951}\) = 84,042
= 4+0.4916
= 4.49 years or 4 years and 5.9 months
Machine – II
Discounted Payback Period = 5 + \(\frac{(15,00,000-14,18,569)}{1,99,505}\)
= 5 + \(\frac{81,431}{1,99,505}\)
= 5+0.4082
= 5.41 years or 5 years and 4.9 months
Net Present Value for:
Machine – I
NPV = ₹ 10,86,909 – ₹ 10,00,000
=₹ 86,909
Machine – II
NPV = ₹ 16,18,074 – ₹ 15,00,000
= ₹ 1,18,074
Internal Rate of Return (IRR) for:
Machine – I
P.V. Factor = \(\frac{\text { Initial Investment }}{\text { Annual Cash Inflow }}=\frac{10,00,000}{3,01,500}\) = 3.31 67
PV factor falls between 15% and 16%
Present Value of Cash inflow at 15% and 16% will be:
Present Value at 15% = 3.353 × 3,01,500 = 10,10,930
Present Value at 16% = 3.274 × 3,01,500 = 9,87,111
IRR = 15 + \(\frac{10,10,930-10,00,0000}{10,10,930-9,87,111} \times(16-15) \)
= 15+ \(\frac{10,930}{23,819} \times 1\)
= 15.4588% = 15.46%
Machine – II
P.V. Factor = \(\frac{15,00,000}{3,93,500}\) = 3.8119
Present Value of Cash inflow at 14% and 15% will be:
Present Value at 14% = 3.888 x 3,93,500 = 1 529,928
Present Value at 15% = 3.785 x 3,93,500 = 14,89,398
IRR = 14 + \(\frac{15,29,928-15,00,000}{15,29,928-14,89,398} \times(15-14) \)
= 14+ \(\frac{29,928}{40,530} \times 1\)
= 14.7384% = 14.74%
(ii) Advise to the Management
Ranking of Machines in Terms of the Three Methods
| Machine – I | Machine – II | |
| Discounted Payback Period | I | II |
| Net Present Value | II | I |
| Internal Rate of Return | I | II |
Advise: Since Machine – I has better ranking than Machine – II, therefore,
Machine: I should be selected.
Question 23.
ANP Ltd. is providing the following information:
Annual cost of saving ₹ 96,000
Useful life 5 years
Salvage value zero
Internal rate of return 15%
Profitability index 1.05
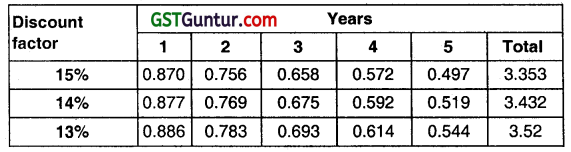
Table of discount factors:
You are required to calculate:
(i) Cost of the project
(ii) Payback period
(iii) Net present value of cash inflow
(iv) Cost of capital (May 2012, 8 marks)
Answer:
(i) Cost of Project
At internal rate of return (IRR) of 15%, the amount of total cash
inflows = cost of the project i.e. total cash outflow
Annual cost savings = ₹ 96,000
Useful life = 5 years
Considering the discount factor table @ 15%, cumulative present value of cash inflows for 5 years is 3.353
Hence, Total Cash inflows for 5 years for the Project is
96,000 × 3.353 = ₹ 3,21,888
Hence, Cost of the Project = ₹ 3,21,888
(ii) Payback Period
Payback period = \(\frac{\text { Cost of the Project }}{\text { Annual Cost Savings }}=\frac{₹ 3,21,888}{96,000}\)
Payback Period = 3.353 years
(iii) Net Present Value (NPV)
NPV = Sum of Present Values of Cash inflows – Cost of the Project
= ₹ 3,37,982.40 – 3,21,888 = ₹ 16,094.40
Net Present Value = ₹ 16,094.40
(iv) Cost of Capital
Profitability index = \(\frac{\text { SumofDiscountedCashinflows }}{\text { Cost of theProject }} \)
1.05 = \(\frac{\text { SumofDiscountedCashinflows }}{3,21,888} \)
∴ Sum of Discounted Cash inflows = ₹ 3,37,982.40
Since, Annual Cost Saving = ₹ 96,000
Therefore, cumulative discount factor for 5 years
= \(\frac{₹ 3,37,982.40}{96,000} \)
From the discount factor table, at discount rate of 13%, the cumulative discount factor for 5 years is 3.52 Hence, Cost of Capital = 13%
![]()
Question 24.
SS Limited is considering the purchase of a new automatic machine which will carry out some operations which are at present performed by manual labour. NM-A1 and NM-A2, two alternative models are available in the market. The following details are collected:

Depreciation will be charged on a straight-line method. The corporate tax rate is 30 percent and the expected rate of return may be 12 percent.
You are required to evaluate the alternatives by calculating the:
(i) Pay-back Period
(ii) Accounting (Average) Rate of Return; and
(iii) Profitability Index or P.V. Index (P.V. factor for 1 @ 12% 0.893;
0.797; 0.712; 0.636; 0.567; 0.507) (Nov 2012, 10 marks)
Answer:
Evaluation of Alternatives
Working Notes:
Depreciation on Machine NM-A1 = \(\frac{20,00,000}{5} \) = 4,00,000
Depreciation on Machine NM-A2 = \(\frac{25,00,000}{5}\) = 5,00,000
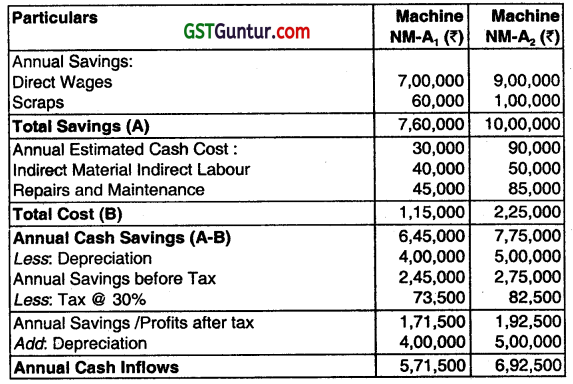
(i) Payback Period
Machine NM-A1 = \(\frac{\text { Total Initial Capital Investment }}{\text { Annual expected after-tax net cashflow }} \)
= \(\frac{20,00,000}{5,71,500} \)
= 3.50 Years
Machine NM- A2 = \(\frac{25,00,000}{6,92,500}\) = 3.61 Years
Decision: Machine NM-A1 is better.
(ii) Accounting (Average) Rate of Return (ARR)
ARR = \(\frac{\text { Average Annual Net Savings }}{\text { Average Investment }} \times 100 \)
Machine NM-A1 = \(\frac{1,71,500}{10,00,000} \times 100\) = 17.1 5%
Machine NM-A2 = \(\frac{1,92,500}{12,50,000} \times 100 \) = 15.4%
Decision: Machine NM-A1 is better.
(Note: ARR may be computed alternatively by taking initial investment ¡n the denominator.)
(iii) Profitability Index or PV Index
Present Value Cash inflow = Annual Cash Inflow × PV factor at 12%
Machine N M-A1 = 571,500 × 3.605 = ₹ 20,60,258
Machine NM-A2 = 6,92,500 × 3.605 = ₹ 24,96,463
PV Index = \(\frac{\text { Present Value of Cashinflow }}{\text { Investment }}\)
Machine NM-A1 = \(\frac{20,60,258}{20,00,000} \) = 1.03
Machine NM-A2 = \(\frac{24,96,463}{25,00,000}\) = 0.9
Decision: Machine NM-A1 is better.
Question 25.
PQR Company Ltd. is considering to select a machine out of two mutually exclusive machines. The company’s cost of capital is 12 percent and corporate tax rate is 30 percent. Other information relating to both machines is as follows:
| Machine-I | Machine-II | |
| Cost of Machine | 15,00,000 | 20,00,000 |
| Expected Life | 5 Yrs. | 5 Yrs. |
| Annual Income (Before Tax and Depreciation) |
₹ 6,25,000 | ₹ 8,75,000 |
Depreciation is to be charged on a straight-line basis:
You are required to calculate:
(i) Discounted Pay Back Period
(ii) Net Present Value
(iii) Profitability Index

(May 2013, 9 Marks)
Answer:
Working Notes:
Depreciation on Machine – I = \(\frac{15,00,000}{5} \) = ₹ 3,00,000
Depreciation on Machine – II = \(\frac{20,00,000}{5}\) = 400 000
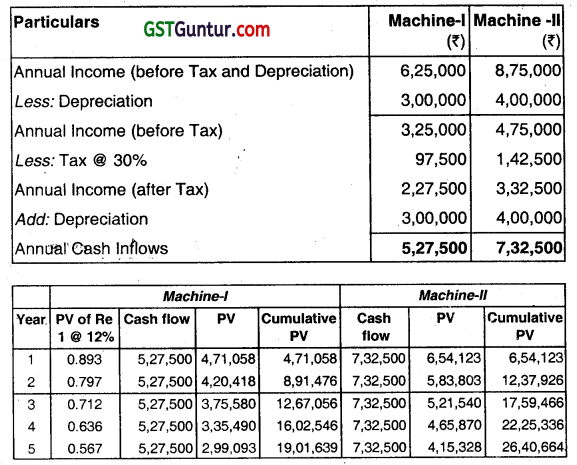
(i) Discounted Payback Period
Machine-I
Discounted Payback period = 3 + \(\frac{(15,00,000-12,67,056}{3,35,490)} \)
= 3 + \(\frac{2,32,944}{3,35,490}\)
= 3+0.6943
= 3.69 years or 3 years 8.28 months
Machine – II
Discounted Payback Period = 3 + \(\frac{(20,00,000-17,59,466)}{4,65,870}\)
= 3+ \(\frac{2,40,534}{4,65,870} \)
= 3+0.5163
= 3.52 years or 3 years 6.24 months
(ii) Net Present Value (NPV)
Machine – I
NPV= 19,01,639 – 15,00,000 = ₹ 4,01,639
Machine-II
NPV = 26,40,664 – 2000,000 = ₹ 6,40,664
(iii) Profitability Index
Machine – I
Profitability Index = \(\frac{19,01,639}{15,00,000}\) = 1.268
Machine – II
Profitability Index = \(\frac{26,40,664}{20,00,000}\) = 1.320
Conclusion:
| Method | Machine- I | Machine -II | Rank |
| Discounted Payback Period | 3.69 years | 3.52 years | II |
| Net Present Value | 4,01,639 | 6,40,664 | II |
| Profitability Index | 1.268 | 1.320 | II |
Question 26.
FH Hospital is considering to purchase a CT scan machine. Presently the hospital is outsourcing the CT-Scan Machine and is earning commission of ₹ 15,000 per month (net of tax). The following details are given regarding the machine:
| ₹ | |
| Cost of CT-Scan machine | 15,00,000 |
| Operating cost per annum (excluding Depreciation) | 2,25,000 |
| Expected revenue per annum | 7,90,000 |
| Salvage value of the machine (after 5 years) | 3,00,000 |
| Expected life of the machine | 5 years |
Assuming tax rate @ 30%, whether it would be profitable for the hospital to purchase the machine?
Give your recommendation under:
(i) Net Present Value Method, and
(ii) Profitability Index Method.
PV factors at 12% are given below:
| Year | 1 | 2 | 3 | 4 | 5 |
| PV factor | 0.893 | 0.797 | 0.712 | 0.636 | 0.567 |
(May 2014, 8 marks)
Answer:
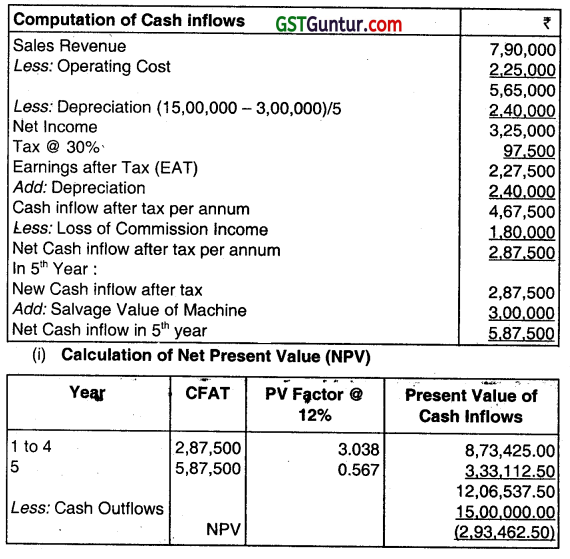
(ii) Calculation of Profitable Index
Profitable Index
= \(\frac{\text { Sum of discounted cash inflows }}{\text { Present value of cash outflows }}=\frac{12,06,537.50}{15,00,000} \)
= 0.804
Advise: Since the net present value is negative and profitability index is also less than 1, therefore, the hospital should not purchase the CT-Scan machine.
Question 27.
Given below are the data on a capital project ‘M’.
Annual cash inflows ₹ 60,000
Useful life 4 years
Internal rate of return 15%
Profitability index 1.064
Salvage value 0
You are required to calculate for this project M:
(I) Cost of project
(ii) Payback period
(iii) Cost of capital
(iv) Net present value
PV factors at different rates are given below:
| Discount factor | 15% | 14% | 13% | 12% |
| 1 year | 0.869 | 0.877 | 0.885 | 0.893 |
| 2 year | 0.756 | 0.769 | 0.783 | 0.797 |
| 3 year | 0.658 | 0.675 | 0.693 | 0.712 |
| 4 year | 0.572 | 0.592 | 0.613 | 0.636 |
(May 2015, 8 marks)
Answer:
(i) Calculation for Cost of Project:
Cost of project at 15% Internal rate of return, the sum of total cash Inflows = Cost of the Project i.e. initial cash outlay.
Annual cash inflow = ₹ 60,000
Useful life = 4 years
Considering discounting factor @ 15%, cumulative cash inflow for 4 years is 2.855
Hence, total cash flow for 4 years for the project = ₹ 60,000 x 2.855
Cost of Project = ₹ 1,71,300
(ii) Calculation for Payback Period:
Pay-back Period = \(\frac{\text { Cost of Project }}{\text { Annual Cashinflow }}\)
= \(\frac{1,71,300}{60,000}\)
Pay-back Period = 2.855 years.
(iii) Calculation for Cost of Capital:
Profitability Index = \(\frac{\text { SumofDiscountedCashInflow }}{\text { Cost of project }} \)
1064 = \(=\frac{\text { Sumof DiscountedCashInflows }}{1,71,300}\)
Sum of discounted cash inflows = ₹ 1,82,263.20
Hence, Cumulative discount factor for four years
= \(\frac{₹ 1,82,263.20}{60,000}\) = 3.038
From the discount factor table, at discount rate of 12% the cumulative discount factor for 5 years is 3.038
Hence, Cost of Capital is 12%.
(iv) Calculation for Net Present value (NPV):
NPV = Sum of Present values of cash inflows – Cost of Project
= 182263.2- 171300
NPV = ₹ 10963.20
![]()
Question 28.
Given below are the data on a capital project ‘C’:
Cost of the project ₹ 2,28,400
Useful life 4 years
Profitability index 1.0417
Internal rate of return 15%
Salvage value 0
You are required to calculate:
(j) Annual cash flow
(ii) Cost of capital
(iii) Net present value(NPV)
(iv) Discounted payback period
Given the following table of discount factors:
| Discount Factor | 15% | 14% | 13% | 12% |
| 1 year | 0.869 | 0.877 | 0.885 | 0.893 |
| 2 years | 0.756 | 0.769 | 0.783 | 0.797 |
| 3 years | 0.658 | 0.675 | 0.693 | 0.712 |
| 4 years | 0.572 | 0.592 | 0.613 | 0.636 |
(May 2016, 8 marks)
Answer:
At IRR NPV is Zero
Cost of Project = Annual cash flow × Commutative factor IRA
2,28,400 = Annual Cash inflow × 2.855
(i) ∴ Annual Cash Inflow = 80,000
(ii) Cost of Capital
Profitabillty Index (PI) = \(\frac{\text { PV of Cash Inflow }}{\text { PV Cash Outflow }} \)
1.0417 = \(\frac{\text { PV of Casl: Inflow }}{2,28,400} \)
∴ PV of Cash Inflow = 2,37,924.28
Annual Cash Inflow × PV factor = PV of Inflow
80,000 × PV Factor = 2,37,924.28
∴ Commutative PV factor = 2.974
(iii) Cost of Capital = 13%
Net Present Value (NPV) = PV of Inflow – Outflow
= 2,37,924.28 – 2,28,400
NPV = 9,524.28

Discounted Payback Period =3+ \(\frac{39,520}{49,040}\) = 3.8059 years
Or = 3 years, 9 Months and 21 days.
Question 29.
X Limited is considering to purchase of new plant worth ₹ 80,00,000. The expected net cash flows after taxes and before depreciation are as follows:
| Year | Net Cash Flows |
| ₹ | |
| 1 | 14,00,000 |
| 2 | 14,00,000 |
| 3 | 14,00,000 |
| 4 | 14,00,000 |
| 5 | 14,00,000 |
| 6 | 16,00,000 |
| 7 | 20,00,000 |
| 8 | 30,00,000 |
| 9 | 20,00,000 |
| 10 | 8,00,000 |
The rate of cost of capital is 10%.
‘fou are required to calculate:
(i) Pay-back period
(ii) Net preseñt value at 10% discount factor
(iii) Profitability index at 10% discount factor
(iv) Internal rate of return with the help of 10% and 15% discount factor
The following present value table is given for you:
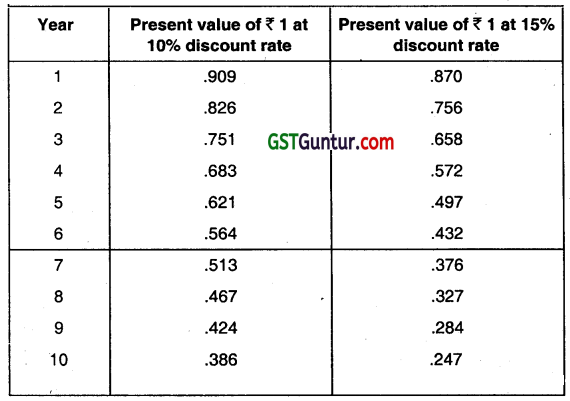
(May 2017, 8 marks)
Answer:
| Year | Cash Flow | Cumulative |
| 0 | 80,00,000 | – |
| 1 | 14,00,000 | 14,00,000 |
| 2 | 14,00,000 | 28,00,000 |
| 3 | 14,00,000 | 42,00,000 |
| 4 | 14,00,000 | 56,00,000 |
| 5 | 14,00,000 | 70,00,000 |
| 6 | 16,00,000 | 86,00,000 |
| 7 | 20,00,000 | |
| 8 | 30,00,000 | |
| 9 | 20,00,000 | |
| 10 | 8,00,000 |
(i) Calculation of Pay-back Period.
Cash Outlay of the Project = ₹ 80,00,000
Total Cash mf low for the first five years = ₹ 70,00,000
Balance of cash outlay left to be paid back in the 6th year = ₹ 10,00,000
Cash inflow for 6th year = ₹ 16,00,000
So the payback period is between and 6th years, i.e.,
= 5 Years + \(\frac{₹ 10,00,000}{₹ 16,00,000}\) = 5.625 Years or 5 years 7.5 months
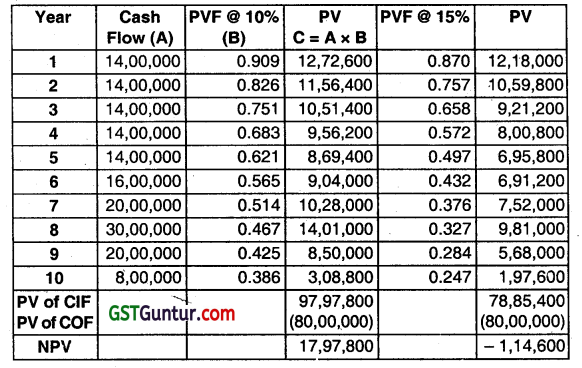
(ii) NPV @ 10% = ₹ 17,97,800
(iii) PI @ 10% = \(\frac{\text { PV of CIF }}{P V \text { of } C O F}=\frac{97,97,800}{80,00,000}\) = 1.225
(iv) IRR = 10 + \(\left[\frac{17,97,800}{17,97,800+114,600} \times 5\right]\)
= 10 + \(\left(\frac{17,97,800}{19,12,400} \times 5\right)\)
= 14.70% (Approx.)
Final Answer:
| 1. Payback Period | 5.625 Years |
| 2. NPV | 17,97,800 |
| 3. PI | 1.225 |
| 4. IRR | 14.70% |
Question 30.
Mr. B will require ₹ 30 lakhs after 10 years from now. He wants to ascertain an amount to be invested in a fund which pays interest @ 10% per annum.
Following options are available to him:
(i) to make annual payment into the fund at the end of each year.
(ii) to invest a lumpsum amount in the fund at the end of the year.
(iii) to make annual payment into the fund in the beginning of each year.
Find out the amount to be invested under each of the options given above.
Factors are as under:
FVIF/CVF(10%,10) = 2.594
FVIFA/CVFA(10%,10) = 15.937
PVIF/PVF (10%, 10) = 0.386
PVIFAIPVFA (10%, 10) = 6.145 (Nov 2017, 5 marks)
Answer:
(I) Here,
FVA = 30,00,000
n =10
i =0.10
Since, FVA = R [FVIFA (I, n)]
FVIFA (10%, 10) = 15.937
R = \(\frac{30,00,000}{15.937}\) = 1,88,241.1997
(ii) Fvn = R [1 + i]n
R = \(\frac{F V_n}{(1+i)^n}\)
R =30,00,000 x 0.386= ₹ 11,58,000
(iii) R = \(\frac{30,00,000}{17.5307}\)
= ₹ 1,71,128.3634.
Question 31.
Kanoria Enterprises wishes to evaluate two mutually exclusive projects X and Y.
The particulars are as under:
| Project X (₹) | Project Y (₹) | |
| Initial Investment | 1,20,000 | 1,20,000 |
| Estimated cash inflows (per annum for 8 years) | ||
| Pessimistic | 26,000 | 12,000 |
| Most Likely | 28,000 | 28,000 |
| Optimistic | 36,000 | 52,000 |
The cut-off rate is 14%. The discount factor at 14% are:
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Discount factor | 0.88 | 0.77 | 0.68 | 0.592 | 0.519 | 0.456 | 0.4 | 0.351 | 0.308 |
Advise management about the acceptability of projects X and Y. (May 2019, 5 marks)
Answer:
Calculation of NPV:
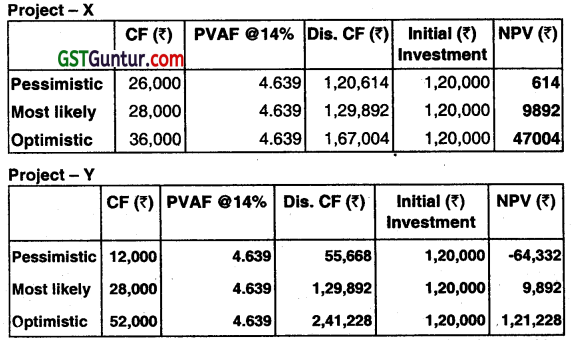
In pessimistic situation, project X will be better as it gives low but positive NPV whereas Project Y yields highly negative NPV under this situation. In most likely situation both the project will give same result. However, in optimistic situation, Project Y wilt be better as it will gives very high NPV. So, project X is a risk less project as it gives positive NPV in all the situations where as Y is a risky project as it will result into negative NPV in pessimistic situations and highly positive NPV in optimistic situation. So acceptability of project will largely depend on the risk taking capacity (Risk seeking Risk a version) of the management.
Question 32.
AT Limited is considering three projects A, B and C. The cash flows associated with the projects are given below:
Cash flows associated with the Three Projects (₹)
| Project | C0 | C1 | C2 | C3 | C4 |
| A | (10,000) | 2,000 | 2,000 | 6,000 | 0 |
| B | (2,000) | 0 | 2,000 | 4,000 | 6,000 |
| C | (10,000) | 2,000 | 2,000 | 6,000 | 10,000 |
You are required to:
(a) Calculate the payback period of each of the three projects.
(b) If the cut-out period is two years, then which projects should be accepted?
(c) Projects with positive NPVs If the opportunity cost of capital is 10 percent.
(d) “Payback gives too much weight to cash flows that occur after the cut-off date”. True or false?
(e) “If a firm used a single cutoff period for all projects, it is likely to accept too many short-lived projects. True or false?
P.V. Factor @ 10%
| Year | 0 | 1 | 2 | 3 | 4 | 5 |
| P.V. | 1.000 | 0.909 | 0.826 | 0.751 | 0.683 | 0.621 |
(May 2019, 10 marks)
Answer:
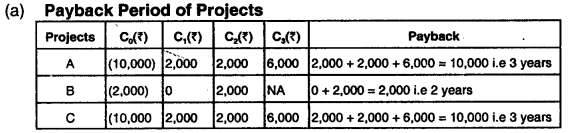
(b) If the standard payback period is 2 years, Project B is the only acceptable project.
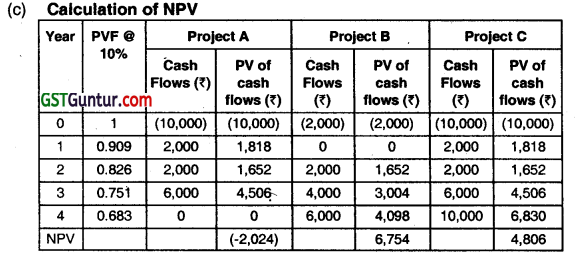
So, Projects with positive NPV are Project B and Project C
(d) False. Payback gives no weightage to cash flows after the cut-off date.
(e) True. The payback rule ignores all cash flows after the cutoff date, meaning that future years’ cash inflows are not considered. Thus, payback is biased towards short-term projects.
![]()
Question 33.
A company has ₹ 1,00,000 available for investment and has identified the following four investments ¡n which to invest.
| Project | Investment (₹) | NPV (₹) |
| C | 40,000 | 20,000 |
| D | 1,00,000 | 35,000 |
| E | 50,000 | 24,000 |
| F | 60,000 | 18,000 |
You are required to optimize the returns from a package of projects within the capital spending limit if
(i) The projects are independent of each other and are divisible.
(ii) The projects are not divisible. (Nov 2019, 5 marks)
Answer:
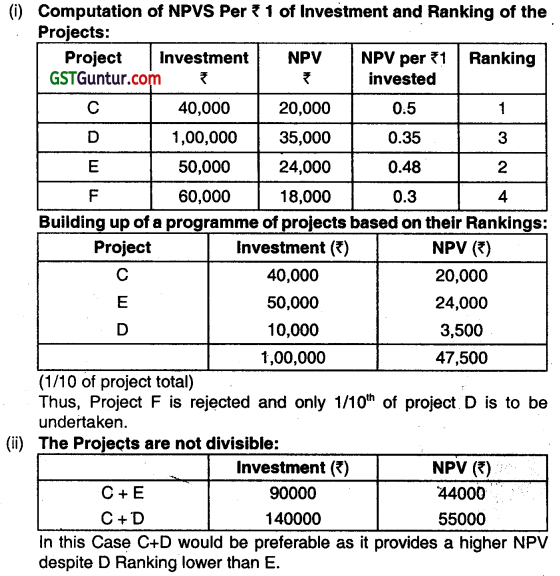
Question 34.
A company wants to buy a machine, and two different models namely A and B are available. Following further particulars are available:
| Particulars | Machine – A | Machine – B |
| Original Cost (₹) | 8,00000 | 6,00,000 |
| Estimated Life in Years | 4 | 4 |
| Salvage Value (₹ ) | 0 | 0 |
The company provides depreciation under Straight Line Method. Income tax rate applicable is 30%. The present value of 1 at 12% discounting factor and net profit before depreciation and tax are as under:

Calculate:
1. NPV (Net Present Value)
2. Discounted pay-back period
3. PI (Profitability Index)
Suggest: Purchase of which machine is more beneficial under Discounted pay-back period method, NPV method and Pl method. (Jan 2021,10 marks)
Question 35.
A company has to make a choice between two projects namely A and B. The initial capital outlay of two Projects are ₹ 1,35,000 and ₹ 2,40,000 respectively for A and B. There will be no scrap value at the end of the life of both the projects. The opportunity Cost of Capital of the company is 16%. The annual income are as under:
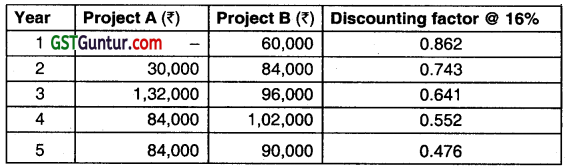
Required:
CALCULATE for each project:
(i) Discounted payback period
(ii) Profitability index
(iii) Net present value
DECIDE which of these projects should be accepted? (, 10 Marks)
Answer:
(i) Discounted payback period: (Refer to Working note 2)
Cost of Project A = ₹ 1,35,000
Cost of Project B = ₹ 2,40,000
Cumulative PV of cash inflows of Project A after 4 years = ₹ 1,53,270
Cumulative PV of cash inflows of Project B after 5 years = ₹ 2,74,812
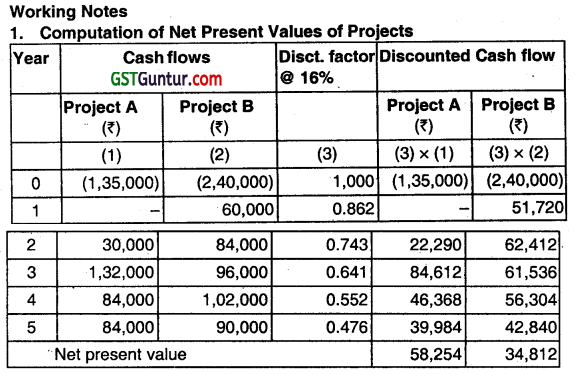
A comparison of projects cost with their cumulative PV clearly shows that the project’s cost will be recovered in less than 4 years and that of project B in less than 5 years. The exact duration of discounted payback period can be computed as follows:
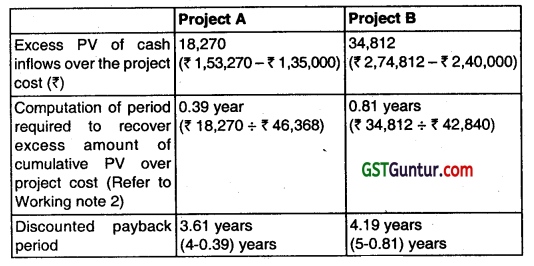
(ii) Profitability Index (PI): = \(\frac{\text { Sum of discounted cash inflows }}{\text { Initian cash outlay }} \)
Profitability Index (for Project A) = \(\frac{₹ 1,93,254}{₹ 1,35,000}\) = 1.43
Profitability Index (for Project B) = \(\frac{₹ 2,74,812}{₹ 2,40,000} \) = 1.15
(iii) Net present value (N PV) (for Project A) = ₹ 58,254
Net present value (NPV) (for Project B) =₹ 34,812
(Refer to Working Note 1)
Conclusion: As the NPV, PI of Project A is higher and Discounted Payback is lower, therefore Project a should be accepted.
Question 36.
BT Pathology Lab Ltd. is using an X-ray machine which reached at the end of their useful lives. Following new X-ray machines are of two different brands with same features are available for the purchase.

Residual Value of both of above machines shall be dropped by 1/3 of Purchase price in the first year and thereafter shall be depreciated at the rate mentioned above. Alternatively, the machine of Brand ABC can also be taken on rent to be returned back to the owner after use on the following terms and conditions:
Annual Rent shall be paid in the beginning of each year and for first year it shall be ₹ 1,02,000.
Annual Rent for the subsequent 4 years shall be ₹ 1,02,500.
Annual Rent for the final 5 years shall be ₹ 1,09,950.
The Rent Agreement can be terminated by BT Labs by making a payment of ₹ 1,00,000 as penalty. This penalty would be reduced by ₹ 10,000 each year of the period of rental agreement.
You are required to:
(a) ADVISE which brand of X-ray machine should be acquired assuming that the use of machine shall be continued for a period of 20 years.
(b) STATE which of the option is most economical if machine is likely to be used for a period of 5 years? The cost of capital of BT Labs is 12%.
Answer:
Since the life span of each machine is different and time span exceeds the useful lives of each model, we shall use Equivalent Annual Cost method to decide which brand should be chosen.
(i) If machine Is used for 20 years Present Value (PV) of cost If machine of Brand XYZ is purchased
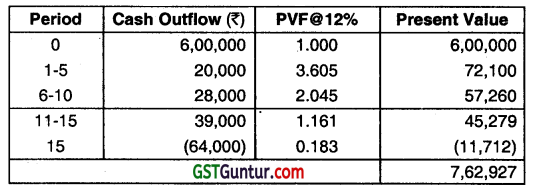
PVAF for 1-15 years 6.811
Equivalent Annual Cost= \(\frac{₹ 7,62,927}{6.811}\) = ₹ 1,12,014
Present Value (PV) of cost of machine of Brand ABC Is purchased
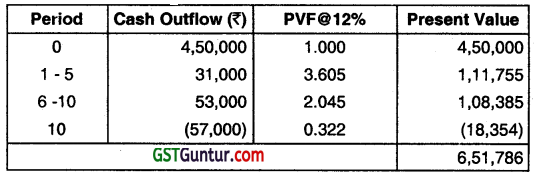
PVAF for 1-10 years 5.65
Equivalent Annual Cost = \(\frac{₹ 6,51,786}{5.65}\) = ₹ 1,15,360
Present Value (PV) of cost if machine of Brand ABC ¡s taken on Rent
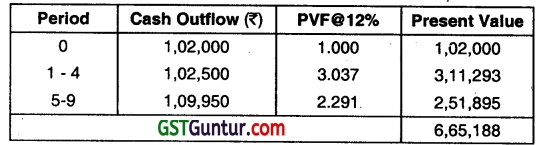
PVAF for 1- 1o years = 5.65
Equivalent Annual Cost = \(\frac{₹ 6,65,188}{5.65} \) = ₹ 1,17,732
Decision: Since Equivalent Annual Cash Outflow is least in case of purchase of Machine of brand XYZ the same should be purchased.
(ii) If machine Is used for 5 years
(a) Scrap Value of Machine of Brand XYZ
= ₹ 6,00,000 – ₹ 2,00,000 – ₹ 6,00,000 × 0.04 × 4= ₹ 3,04,000
(b) Scrap Value of Machine of Brand ABC
= ₹ 4,50,000 – ₹ 1,50,000 – ₹ 4,50,000 × 0.06 × 4 = ₹ 1,92,000
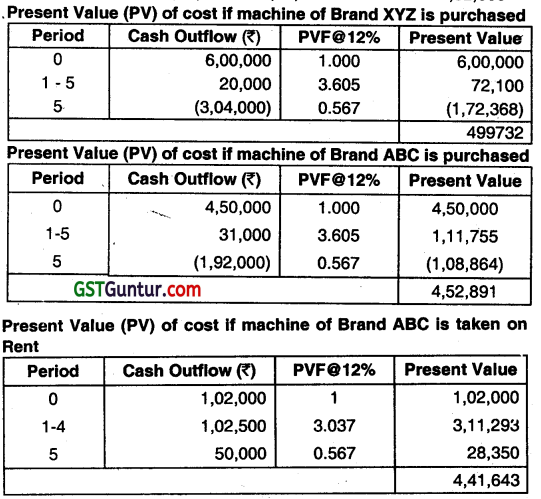
Decision: Since Cash Outflow is least in case of lease of a Machine of brand ABC the same should be taken on rent.