Indices – CA Foundation Maths Study Material

This Indices – CA Foundation Maths Study Material is designed strictly as per the latest syllabus and exam pattern.

Indices – CA Foundation Maths Study Material

If a number x is multiplied 5 times written as.
x. x. x. x. x. = x⁵.
Here “x” is called BASE and 5 is called Power or Index.

Some Related Formulae.
1. a^m = a × a × a × …………… to m times.

2. a⁰ = 1 where a ≠ o; ∞

3. a^-1 = \(\frac{1}{a}\)

4. a^-m = \(\frac{1}{a^m}\)

• a^m × aⁿ = a^m+n
• a^m × aⁿ × a^r × ………. = a^m+n+r ……
• \(\frac{a^m}{a^n}\) = a^m-n
• \(\frac{a^m}{a^n}=\frac{1}{a^{n-m}}\)
• (a^m)ⁿ = a^mn
• a^mn ≠ a^mn
• If a^m = b^m Then a = b
• If a^m = aⁿ Then m = n
• \(\sqrt[m]{a^n}\) = a^{\(\frac{n}{m}\)}
• √a = a^{\(\frac{1}{2}\)}
• 3√a = a^{\(\frac{1}{3}\)}
• If a^m = k ⇒ a = k^1/m
• If a^m = kⁿ ⇒ a = k^n/m
• If a^1/m = k ⇒ a = k^m
• If a^1/m = kⁿ ⇒ a = k^mn
• \(\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\)
• (ab….)^m = a^m.b^m
• \(\sqrt[m]{a b \ldots \ldots \ldots}=\sqrt[m]{a} \cdot \sqrt[m]{b} \ldots \ldots .\)
• \(\sqrt{a b}\) = √a. √b.
• \(\left(\frac{a}{b}\right)^m=\left(\frac{b}{a}\right)^{-m}\)

5. If a^b = b^a Then
Either (i) a = b
or (ii) If a = 2
Then b = 4
or (Hi) If a = 4
Then b = 2

6. If a > 1 and x < y
Then a^x < a^y

Calculator Tricks

1. For a^+m
Steps (i) Type a
(ii) Press x button.
(Hi) Continue pressing “=” button (Power -1 = m -1) times.

Example
4⁺⁵ = 1024
Type 4 Then Press x button Then “=” button 4 times; we get the result.

2. For a^-m
Steps (i) Type “a”
(if) Press ÷ button.
(iii) Continue pressing “=” button (Power = m) times
Example:
2^-4 = 0.0625
Type base 2 then press button then continue pressing = button 4 times. We get the required result.

3. For (1.05)⁶⁰
1st Method:
Type base 1.05
Then press “×” button 60 – 1 = 59 times.
IInd Method:
(1.05)⁶⁰ = [(1.05)¹²]⁵
1st work for 1.0512
Then “×” button and work for power 5.

Work As.:
Type 1.05 then press × button
Then press = button 12 – 1 = 11 times
Then press × button and continue
Pressing = button 5-1=4 times.
We get the required result.

Previous Year Exam Questions

Question 1.
Value of (a^1/8 + a^-1/8)(a^1/8 – a^-1/8)
(a^1/4 + a^-1/4)(a^1/2 + a^-1/2) is:
(a) a + \(\frac{1}{a}\)
(b) a – \(\frac{1}{a}\)
(c) a² + \(\frac{1}{a^2}\)
(d) a² – \(\frac{1}{a^2}\)
Answer:
[a^1/8 + a^-1/8][a^1/8 – a^-1/8][a^1/4 + a^-1/4][a^1/2 + a^-1/2]
[Use Formula (a + b)(a – b) = a² – b²]
= [(a^1/8)² – (a^1/8)²][a^1/4 + a^-1/4][a^1/2 + a^-1/2]
= (a^1/4 – a^-1/4)(a^1/4 + a^-1/4)(a^1/2 + a^-1/2)
= [(a^1/4)² – (a^-1/4)²][a^1/2 + a^-1/2]
= (a^1/2 – a^-1/2)(a^1/2 + a^-1/2)
= (a^1/2)² – (a^-1/2)² = a – a^-1 = a – \(\frac{1}{a}\)
(b) is correct

Question 2.
Simplification of \(\frac{x^{m+3 n} x^{4 m-9 n}}{x^{6 m-6 n}}\) is :
(a) x^m
(b) x^-m
(c) xⁿ
(d) x^-n
Answer:
\(\frac{x^{m+3 n} x^{4 m-9 n}}{x^{6 m-6 n}}\) = x^{m+3n+4m-9n-6m+6n} = x^-m = x^-m
(b) is correct

Question 3.
On simplification \(\frac{1}{1+z^{a-b}+z^{a-c}}+\frac{1}{1+z^{b-c}+z^{b-a}}+\frac{1}{1+z^{c-a}+z^{c-b}}\) reduces to : [1 Mark, Aug. 2007]
(a) \(\frac{1}{z^{2(a+b+c)}}\)
(b) \(\frac{1}{z^{(a+b+c)}}\)
(c) 1
(d) 0
Answer:
Tricks
\(\frac{1}{1+Z^{a-b}+Z^{a-c}}+\frac{1}{1+Z^{b-c}+Z^{b-a}}+\frac{1}{1+Z^{c-a}+Z^{c-a}}\)
= 1 [it is in cyclic order]

Question 4.
If 4^x = 5^y = 20^z then z is equal to:
(a) xy
(b) \(\frac{x+y}{x y}\)
(c) \(\frac{1}{x y}\)
(d) \(\frac{x y}{x+y}\)
Answer:
(d)
Let 4^y = 5^y = 2o^z =k
or 4 = k^1/x; 5 = k^1/y; 20 = k^1/z
∴ 20 = 4 × 5

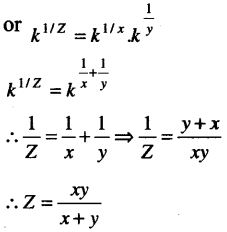
(d) is correct

Question 5.
\(\left(\frac{\sqrt{3}}{9}\right)^{5 / 2}\left(\frac{9}{3 \sqrt{3}}\right)^{7 / 2}\) × 9 is equal to: [1 Mark, Nov. 2007]
(a) 1
(b) √3
(c) 3√3
(d) \(\frac{3}{9 \sqrt{3}}\)
Answer:

= (3^-4)^1/2.3² = 3^-2.3² = 3^-2+2 = 3⁰ = 1
(a) is correct.

Question 6.
If 2^x – 2^{x – 1} = 4, then the value of x^x is : [1 Mark, Feb. 2008, June 2010]
(a) 2
(b) 1
(c) 64
(d) 27
Answer:
2^x – 2^x-1 = 4
or 2^x-1 (2 – 1) = 4
or 2^x-1 x1 = 22
or 2^x-1 = 22
x – 1 = 2
😡 = 3
…x^x = 3³ =27
(d) is Correct
Tricks : Go by choices
For (d) 27 = 3³ = x^x
x = 3
Put x = 3 in 2^x – 2^x-1 = 4
It satisfies it (d) is correct

Question 7.
If x = y^a, y = z^b and z = x^c then abc is : [1 Mark, June 2008]
(a) 2
(b) 1
(c) 3
(d) 4
Answer:
It x = y^a; y = Z^b & Z = x^c
Then abc = 1
Tricks : It is in cyclic order.
(b) is correct
Tricks : See Quicker BMLRS example

Question 8.
If x = 3^1/3 + 3^-1/3 then find value of 3x³ – 9x. [1 Mark, June 2009]
(a) 3
(b) 9
(c) 12
(d) 10
Answer:
Detail Method
It x = 3^1/3 + 3^-1/3 ……….. (I)
Cubing on both sides; we get x³ =(3^1/3)³ + (3^-1/3)³ +3.3^1/3.3^-1/3(3^1/3 + 3^-1/3)
= 3 + 3^-1 + 3 × 1 × x
or x³ = 3 + \(\frac{1}{3}\) + 3x
or x³ – 3x = \(\frac{9+1}{3}\)
or 3x² – 9x = 10
∴ (d) is correct
Tricks See Quicker BMLRS for CA-Found.

Question 9.
Find the value of: [1 – {1 – (1 – x²)^-1}^-1]^-1/2 is
(a) 1/x
(b) x
(c) 1
(d) none of these
Answer:

∴ (b) is correct

Question 10.
\(\frac{2^n+2^{n-1}}{2^{n+1}-2^n}\)
(a) 1/2
(b) 3/2
(c) 2/3
(d) 1/3
Answer:

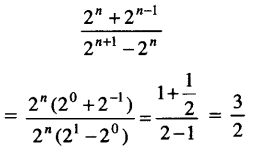
∴ (b) is correct
Tricks: Put n = 1

Question 11.
If 2^x × 3^y × 5^z = 360. Then what is the value of x, y, z. ? [1 Mark, Dec. 2009]
(a) 3, 2, 1
(b) 1,2,3
(c) 2, 3, 1
(d) 1, 3, 2
Answer:
If 2^x × 3^y × 5^z = 360
2^x × 3^y × 5^z = 2³ × 3² × 5¹
Comparing it; we get
x = 3; y = 2; z = 1;
∴ (a) is correct
Tricks : Go by choices.
For (a) x = 3; y = 2; Z = 1
LHS= 2³ × 3² × 5¹ =360 = RHS.
(a) is correct

Question 12.
The recurring decimal 2.7777 ………. can be expressed as: [1 Mark, Dec. 2010]
(a) 24/9
(b) 22/9
(c) 26/9
(d) 25/9
Answer:
Tricks : Go by choices.
By calculator
(a) \(\frac{24}{9}\) = 2.666 …………………. ≠ 2.777
(b) \(\frac{22}{9}\) = 2.444 ……….. ≠ 2.777
(c) \(\frac{26}{9}\) = 2.888 …………… ≠ 2.77
(d) \(\frac{25}{9}\) = 2.777
(d) is correct

Question 13.
The value of \(\frac{\left(3^{n+1}+3^n\right)}{\left(3^{n+3}-3^{n+1}\right)}\) is equal to:
(a) 1/5
(b) 1/6
(c) 1/4
(d) 1/9
Answer:
(b) Tricks :
Put n = 0

Question 14.
Find the value of X, if x.(x)^1/3 = (x^1/3)^z. [1 Mark, Dec. 2012]
(a) 3
(b) 4
(c) 2
(d) 6
Answer:
(b) is correct
x.x^{\(\frac{1}{3}\)} = x^{\(\frac{x}{3}\)}
or x^{1+\(\frac{1}{3}\)} = x^x/3
∴ 1 + \(\frac{1}{3}=\frac{x}{3}\)
∴ \(\frac{4}{3}=\frac{x}{3}\)
∴ x = 4
(b) is correct.

Question 15.
If \(\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}\) = 0; then find the value of \(\left[\frac{a+b+c}{3}\right]^3\) =
(a) 9abc
(b) \(\frac{1}{9 a b c}\)
(c) abc
(d) \(\frac{1}{a b c}\)
Answer:
(c) is correct

Tricks:
Let a = -1; b= -1 and c =8, because \(\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}=\sqrt[3]{-1}+\sqrt[3]{-1}+\sqrt[3]{8}\)
= -1 – 1 + 2 = 0(R.H.S) ∴ \(\left[\frac{a+b+c}{3}\right]^3=\left[\frac{-1-1+8}{3}\right]^3\) = (2)³ = 8
= (-1).(-1).(8) = abc
∴ (c) is correct

Question 16.
The value of
\(\left(\frac{y^a}{y^b}\right)^{a^2+a b+b^2}\left(\frac{y^b}{y^c}\right)^{b^2+b c+c^2}\left(\frac{y^c}{y^a}\right)^{c^2+c a+a^2}\) = . [1 Mark, June 2014]
(a) y
(b) -1
(c) 1
(d) None
Answer:
(c) is correct
Tricks: Cyclic order

Question 17.
If p^x = q, q^y = r, r^z = p⁶, then the value of xyz is ……….[1 Mark, June 2015]
(a) 0
(b) 1
(c) 3
(d) 6
Answer:
q^y = r ⇒ (p^x)^y = r ⇒ r = p^xy
Now r^z = p⁶ ⇒ (p^xy)^z = p⁶ ⇒ p^xyz = p⁶
xyz = 6

Question 18.
The value of \(\frac{x^2-(y-z)^2}{(x+z)^2-y^2}+\frac{y^2-(x-z)^2}{(x+y)^2-z^2}+\frac{z^2-(x-y)^2}{(y+z)^2-x^2}\). [1 Mark, June 2016]
(a) 0
(b) 1
(c) -1
(d) ∞
Answer:
(b) is correct

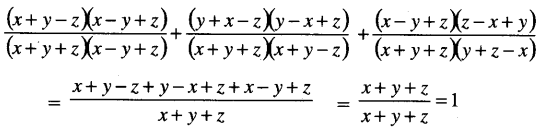
Tricks : Cyclic order

Question 19.
If 3^x = 5^y = (75)^z then
(a) \(\frac{1}{x}+\frac{2}{y}=\frac{1}{z}\)
(b) \(\frac{2}{x}+\frac{1}{y}=\frac{1}{z}\)
(c) \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\)
(d) None
Answer:
See Short Cut Tricks Book “QUICKER BMLRS”
3^x = 5^y = (75)^z ………(1)
3¹ × 5² = 75¹ ………(2)

Tricks:
Power of (2) ÷ power of (1)
and put + sign at the place of “×”
We get \(\frac{1}{x}+\frac{2}{y}=\frac{1}{z}\)
So, (a) is correct

Question 20.
If abc = 2, then the value of \(\frac{1}{1+a+2 b^{-1}}+\frac{1}{1+\frac{b}{2}+c^{-1}}+\frac{1}{1+a^{-1}+c}\) = [1 Mark, June 2016]
(a) 1
(b) 2
(c) \(\frac{1}{2}\)
(d) \(\frac{3}{5}\)
Answer:
TRICKS
“Put a = 1, b = 2 & c = 1. So that abc = 2” in the given question. We get
\(\frac{1}{1+1+\frac{2}{2}}+\frac{1}{1+\frac{2}{2}+1^{-1}}+\frac{1}{1+1^{-1}+1}\) = 1
Option (a) is correct.

Question 21.
If a = \(\frac{\sqrt{6}+\sqrt{5}}{\sqrt{6}-\sqrt{5}}\), b = \(=\frac{\sqrt{6}-\sqrt{5}}{\sqrt{6}+\sqrt{5}}\) then the value of \(\frac{1}{a^2}+\frac{1}{b^2}\) is [1 Mark, June 2017]
(a) 486
(b) 484
(c) 482
(d) 500
Answer:

Option (a) is correct.

Question 22.
If u^5x = v^5y = w^5z and u² = vw then xy + zx – 2yz
(a) 0
(b) 1
(c) 2
(d) None of these
Answer:
(a) u^5x = v^5y = w^5z ⇒ u^x = v^y = w^z
Tricks : See Quicker BMLRS Chapter : Indices
u² = vw;
∴ \(\frac{2}{x}=\frac{1}{y}+\frac{1}{z}=\frac{y+z}{y z}\)
or ; xy + zx = 2yz
or; xy + zx -2yz = 0

Question 23.

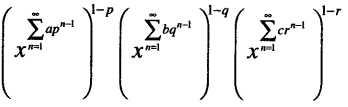
(a) x^-(ap+bq+cr)
(b) x^a+b+c
(c) x^(ap+bq+cr)
(d) x^abc [1 Mark, June 2018]
Answer:
(b)

= x^a.x^b.x^c
= x^a+b+c
Option (b) is correct.

Question 24.
\(\frac{2^n+2^{n-1}}{2^{n+1}-2^n}\)
(a) \(\frac{1}{2}\)
(b) \(\frac{3}{2}\)
(c) \(\frac{2}{3}\)
(d) \(\frac{1}{3}\) [1 Mark, May 2018]
Answer:
(b)
Tricks:
Put minimum power = n – 1 = 0 or n = 1 in the question
∴ \(\frac{2^n+2^{n-1}}{2^{n+1}-2^n}=\frac{2^1+2^{1-1}}{2^{1+1}-2^1}=\frac{2+1}{4-2}=\frac{3}{2}\)

Question 25.
\(\frac{2^{m+1} \times 3^{2 m-n+3} \times 5^{n+m+4} \times 6^{2 n+m}}{6^{2 m+n} \times 10^{n+1} \times 15^{m+3}}\) [1 Mark, Nov. 2018]
(a) 3^2m-2n
(b) 3^2n-2m
(c) 1
(d) None
Answer:
Tricks
Put m = n = 0 in this equation. \(\frac{2^{m+1} \times 3^{2 m-n+3} \times 5^{n+m+4} \times 6^{2 n+m}}{6^{2 m+n} \times 10^{n+1} \times 15^{m+3}}\) = 1

Question 26.
If 2^x = 3^y2 = 12^z2 then [1 Mark, June 2019]
(a) \(\frac{1}{x^2}+\frac{1}{y^2}=\frac{1}{z^2}\)
(b) \(\frac{1}{x^2}+\frac{2}{y^2}=\frac{1}{z^2}\)
(c) \(\frac{1}{x^2}+\frac{2}{y^2}=\frac{1}{z^2}\)
(d) None
Answer:
∵ 2^x2 = 3^y2 = 12^z2 ………..(1) (Given)

Tricks:
Factorize 12 in terms of 2 & 3. We get
2² × 3¹ = 12¹ ……….(2)
Always write as power of base of (2) ÷ Power on same base of 1 ; put “+”
Sign at the place of “×” Sign. So;
\(\frac{2}{x^2}+\frac{1}{y^2}=\frac{1}{z^2}\)
So (c) is correct.

Details
(c) is correct.