Index Numbers – CA Foundation Statistics Solutions

Index Numbers – CA Foundation Statistics Notes is designed strictly as per the latest syllabus and exam pattern.

Index Numbers – CA Foundation Statistics Notes

Previous Year Exam Questions

Question 1.
The number of test of Adequacy is: [1 Mark, Nov. 2006]
(a) 2
(b) 3
(c) 4
(d) 5
Solution:
(c) 4
Number of Test of Adequacy are 4. They are.
(a) Unit test
(b) Time reversal test
(c) Factor reversal test
(d) Circular test

Question 2.
Bowley’s index number is expressed in terms of: [1 Mark, Feb. 2007]

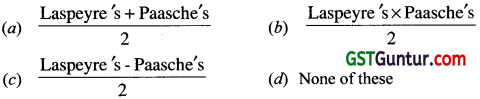
Solution:
(a)

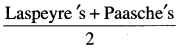
Question 3.
Fisher’s ideal formula for calculating index number satisfies the _ : [1 Mark, Feb. 2007]
(a) Unit Test
(b) Factor Reversal Test
(c) Both(a)&(b)
(d) None of these
Solution:
(c) Both(a)&(b)

Question 4.
Circular Test is satisfied by : [1 Mark, May 2007]
(a) Paasche’s Index Number
(b) The simple geometric mean of price relatives and the weighted aggregative with fixed weights
(c) Laspeyre’s Index Number
(d) None of these
Solution:
(b) The simple geometric mean of price relatives and the weighted aggregative with fixed weights

Question 5.
From the following data:

Group	A	B	C	D	E	F
Group Index:	120	132	98	115	108	95
Weight	6	3	4	2	1	4

The general index is given by : [1 Mark, May 2007]
(a) 113.54
(b) 115.30
(c) 117.92
(d) 111.30
Solution:
(d) 111.30
(d) Group Group Index (i) Weight (w)

Question 6.
Cost of living index numbers are also used to find real wages by the process of: [1 Mark, Aug. 2007]
(a) Base shifting
(b) Splicing of index numbers
(c) Deflating of index numbers
(d) None of these
Solution:
(c) Deflating of index numbers
Real wage is determined after dividing the money by the Cost of Living Index by using the formula.

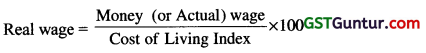
Question 7.
The prices of a commodity in the years 1975 and 1980 were 25 and 30 respectively, Price Relative of 1975 on 1980 is
[1 Mark, Aug. 2007]
(a) 113.25
(b) 83.33
(c) 109.78
(d) None
Solution:
(b) 83.33

Question 8.
From the following data :

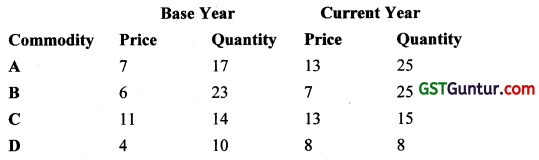
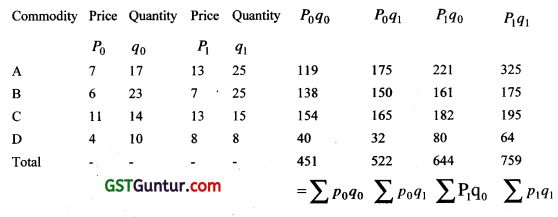
The Marshal Edgeworth index number is : [1 Mark, Aug. 2007]
(a) 144.19
(b) 143.91
(c) 4900
(d) 140.31
Solution:
(a) 144.19
CALCULATIONS FOR MARSHALL EDGE WORTH INDEX

Question 13.
Laspeyre’s and Paasche’s Method Time Reversal Test: [1 Mark, June 2008]
(a) Do not satisfy
(b) Satisfy
(c) Depends on the case
(d) Can’t say
Solution:
(a) Paasche’s formula also do not satisfy Time Reversal test.

Question 14.
Chain index is equal to:

Solution:
(b)

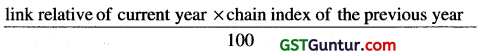
Question 15.
In 2004 for working class people wheat was selling at an average price of ₹ 16 per 20 kg, cloth at ₹ 2 per meter, house rent ₹ 30 per house and other items at ₹ 10 per unit By 2005 cost of wheat rose by ₹ 4 per 20 Kg, house rent by ₹ 15 per house and other items doubled in price. The working class cost of living index for the year 2005 (with 2004 as base) was 160. By how much did cloth rose in price during the period: [1 Mark, June 2008]
(a) 1.28
(b) 0.99
(c) 1.73
(d) 1.30
Solution:
(d) 1.30
Let the Price of cloth be X in 2005
By applying simple average of price relative method.

P₀₁ = \(\frac{\sum \frac{\mathrm{P}_1}{\mathrm{P}_0} \times 100}{\mathrm{~N}}\) ⇒ 160 = \(\frac{475+50 x}{4}\)
⇒ X = 3.30, So, increase in Cloth Price = 3.30 – 2 = 1.30

Question 16.
The ratio of price of the single commodity in a given period to its price in another period is called: [1 Mark, June 2008]
(a) Price Ratio
(b) Price Relative
(c) Base Period
(d) None of these
Solution:
(b) Price Relative
P₀₁ = \(\frac{P_1}{P_0}\)

Question 17.
Consumer Price Index Number goes up from 100 to 200 and salary of a worker is also raised from 300 to 500 The Real Wage is [1 Mark, Dec. 2018)
(a) 300
(b) 250
(c) 600
(d) 350
Solution:
(b) 250
The following data is:

Question 18.
Using following data, find Paasche’s Index Number [1 Mark, Dec. 2008]

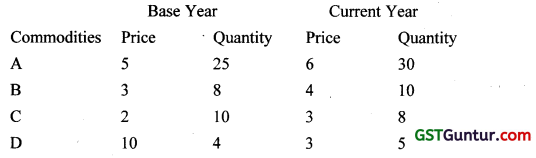
(a) 109.21
(b) 105.28
(c) 110.32
(d) 120.21
Solution:
(b) 105.28

Question 19.
The Circular Test is known as :
(a) P₀₁ × P₁₂ × P₂₀ = 1
(b) P₁₂ × P₀₁ × P₂₀ = 1
(c) P₂₀ × P₁₂ × P₀₁ = 1
(d) P₀₂ × P₂₁ × P₁₂ = 1
Solution:
(a) P₀₁ × P₁₂ × P₂₀ = 1

Question 20.
Fisher’s Index is based on:- [1 Mark, Dec. 2009]
(a) Arithmetic Mean of Laspeyre and Paasche
(b) Geometric Mean of Laspeyre and Paasche
(c) Harmonic Mean of Laspeyre and Paasche
(d) Median of Laspeyre and Paasche
Solution:
(b) Fisher’s ideal price index is the geometric mean of Laspeyre’s index and Paasche’s index.

Question 21.
In Paasche’s index,weights are based on : [1 Mark, Dec. 2009]
(a) Current year quantities
(b) Base year quantities
(c) Weighted average prices
(d) None of these
Solution:
(a) Current year quantities
In Paasche’s index, the quantity weights of the current year are used.

Question 22.
Fisher’s ideal index does not satisfy: [1 Mark, Dec. 2009]
(a) Time Reversal Test
(b) Factor Reversal Test
(c) Unit Test
(d) Circular test
Solution:
(d) Circular test
Fisher’s ideal index satisfies all other tests except the Circular Test.

Question 23.
_____ P₀₁Q₀₁ = \(\frac{\sum P_1 Q_1}{\sum P_0 Q_0}\) following test satisfies the above? [1 Mark, Dec. 2009]
(a) Time Reversal Test
(b) Factor Reversal Test
(c) Circular Test
(d) None of these
Solution:
(b) Factor Reversal Test
Symbolically : P₀₁ × Q₀₁ = V₀₁
P₀₁ × Q₀₁ = \(\frac{\sum P_1 Q_1}{\sum P_0 Q_0}\)
This test is satisfied only by Fisher’s ideal index Number.

Question 24.
Time reversal & factor reversal are: [1 Mark, Dec. 2009]
(a) Quantity Index
(b) Ideal Index
(c) Price Index
(d) Test of Consistency
Solution:
(d) Test of Consistency

Question 25.
In Laspeyres Index Number ____ are used as weights? [1 Mark, Dec. 2009]
(a) Base year price
(b) Current year price
(c) Base year quantities
(d) Current year quantities
Solution:
(c) Base year quantities
Laspeyre’s index = \(\frac{\sum P_1 Q_0}{\sum P_0 Q_0}\)
Therefore from the above we conclude that base year quantities are used as weights in Laspeyre’s index.

Question 26.
In the data group Bowley’s and Laspeyre’s index number is as follows. Bowley’s index number= 150, Laspeyre’s index number = 180 then Paasche’s index number is
(a) 120
(b) 30
(c) 165
(d) None of these
Solution:
(a) 120
∵ Dorbish and Bowley’s Index No. \(=\frac{\text { Laspeyere ‘s }+\text { Paasche ‘s I.No. }}{2}\)
∵ 150 = \(=\frac{180+\text { Paasche ‘s }}{2}\)
⇒ 180 + Paasche’s = 300
∴ Paasche’s Index No. = 120

Question 27.
Consumer price index is commonly known as [1 Mark, June 2010]
(a) Chain Based index
(b) Ideal index
(c) Wholesale price index
(d) Cost of living index.
Solution:
(d) Cost of living index.

Question 28.
Find the Paasche’s index number for prices from the following data taking 1970 as the base year. [1 Mark, June 2010]

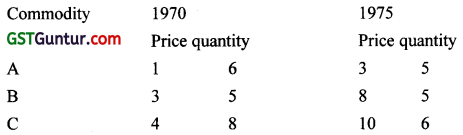
(a) 261.36
(b) 265.48
(c) 274.32
(d) 282
Solution:
(a) 261.36

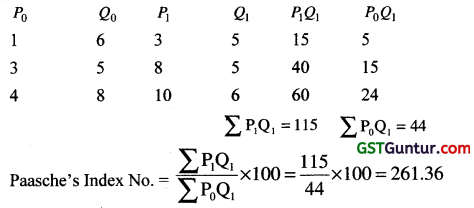
Question 29.
The life expectancy, E of male is a linear function of time (year). It is given that in 1980 the life expectancy was 70 years and in 2000 it was 75 years. Make a prediction of life expectancy in 2012. [1 Mark, June 2010]
(a) 78
(b) 80
(c) 82
(d) 84
Solution:
(a) 78
Given E = at + c,
Where t = Deviation of time from base year 1980
(E being a liner function of time t)
In 1980, t = 1980 – 1980 = 0
The eqn. is
E = a.0 + c = 70 , So, c = 70
In year 2000, t = 2000 – 1980 = 20
E = a.20 + c = 75
So, 20 a +70 = 75
a = 5/20 = 0.25
The Eqn. is E = 0.25t + 70
For year 2012, t = 2012 – 1980 = 32
E = (0.25).(32) + 70 = 78

Question 30.
If Laspeyre’s index number is 90 and Paasche’s index number is 160 then , Fisher’s index number will _____.
[1 Mark, Dec. 2010]
(a) 144
(b) 120
(c) 125
(d) None of these
Solution:
(b) 120
Fisher’s index No.= \(\sqrt{\text { Laspeyre’s I.No. } \times \text { Paasche’s I.No. }}\)
Fisher’s index no. = \(\sqrt{90 \times 160}\) = 120

Question 31.
Wholesale Price Index (WPI) is given by: [1 Mark, June 2011]
(a) Marshall-Edgeworth Index
(b) Laspeyre’s Index
(c) Paasche’s Index
(d) None
Solution:
(b) Laspeyre’s Index

Question 32.
Fisher’s Ideal index is obtained by: [1 Mark, June 2011]
(a) Arithmetic Mean of Laspeyre’s & Paasche’s index
(b) Geometric Mean of Laspeyre’s & Paasche’s index
(c) Sum of Laspeyre’s & Paasche’s index
(d) None of them
Solution:
(b) Geometric Mean of Laspeyre’s & Paasche’s index
Fisher ideal index \(=\sqrt{\text { Laspeyre’s Price Index } \times \text { Paasche’s Price Index }}\)

Question 33.
The index number of prices at a place in the year 2008 is 225 with 2004 as the base year then there is: [1 Mark, June 2011]
(a) average 125% increase in prices
(b) average 225% increase in prices.
(c) average 100% increase in prices
(d) None of the above.
Solution:
(a) Let the price of base year 2004 = 100
∴ the Price of current year 2008 = 225
% Increase in Price = 225 – 100 = 125 %

Question 34.
Fishers Ideal Index Number not satisfies _____ [1 Mark, Dec. 2011]
(a) Unit Test
(b) Time Reversal Test
(c) Circular Test
(d) Factor Reversal Test
Solution:
(c) Circular Test
Fishers Ideal index Number does not satisfies Circular Test.

Question 35.
If the price of all commodities in a place has increased 20% in Comparison to the base period prices, then the index number of prices for the place is now _____ [1 Mark, Dec. 2011]
(a) 100
(b) 120
(c) 20
(d) 150
Solution:
(b) 120
Index No. of current year = 100 + 20 = 120

Question 36.
If ΣP₀Q₀ = 116, Σp_oQ₁ = 14o ΣP₁Q₀ = 97, ΣP₁Q₁ = 117 then Fisher’s ideal index number is …………
(a) 184
(b) 83.59
(c) 119.66
(d) 120
Solution:
(b) 83.59

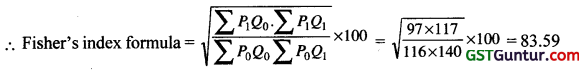
Question 37.
Find the Paasche’ s Index number for price from the following data taking 1970 as the base year. [1 Mark, June 2012]
Solution:
(a) Given :

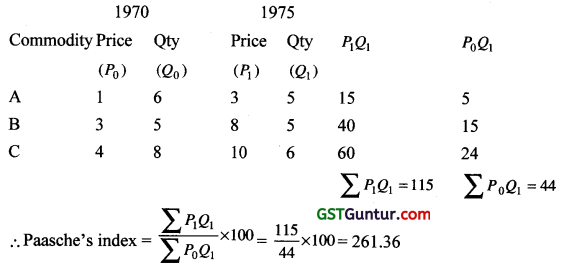
Question 38.
If Fisher’s index = 150 and Paasche’s Index = 144, then Laspeyre’s index is _____ [1 Mark, Dec. 2012]
(a) 147
(b) 156.25
(c) 104.17
(d) 138
Solution:
(b) 156.25
Given Fisher’s index = 150 and Paasche’s index = 144
∴ Fisher’s index \(=\sqrt{\text { Laspeyre’s } \times \text { Paasche’s }}\)
150 \(=\sqrt{\text { Laspeyre’s } \times 144}\)
Squaring on both sides; we get
150 × 150 = Laspeyre’s × 144
Laspeyre’s index = \(\frac{150 \times 150}{144}\) = 156.25
Tricks : GBC

Question 39.
Net monthly of an employees was ₹ 3,000. The consumer price index number in 1985 is 250 with rightly compensated then the additional dearness allowance to be paid to the employee is: [1 Mark, Dec. 2012]
(a) ₹ 4,000
(b) ₹ 4,800
(c) ₹ 5,500
(d) ₹ 4,500
Solution:
(d) ₹ 4,500
Given,
Net monthly salary = ₹ 3,000 in 1980
Consumer price index in 1985 with 1980 as the base year = 250
∴ In 1985 then his monthly salary will be = \(\frac{250 \times 3,000}{100}\) = ₹ 7,500
∴ The Dearness allowance to be paid to the employee = ₹ (7,500 – 3,000) = ₹ 4,500

Question 40.
Time Reversal Test is satisfied by [1 Mark, June 2013]
(a) Fisher’s ideal index
(b) Dorbish Bowley’s index
(c) Laspeyre’s index
(d) None of these
Solution:
(a) Fisher’s ideal index
(a) is correct

Question 41.
Bowley’s Index Number = 150, Laspeyre’s index = 180 then Paasche’s index number is _____ [1 Mark, June 2013]
(a) 120
(b) 130
(c) 105
(d) None
Solution:
(a) 120
(a) is correct
Tricks : Go by choices
Bowley’s Index No. = \(\frac{L+P}{2}\) = \(\frac{120+180}{2}\) = 150
∴ (a) is correct

Question 42.
In 2005 price index is 286 with base 1995 then how much price increased in 2005 with base 1995? [1 Mark, June 2013]
(a) 286%
(b) 386%
(c) 86%
(d) 186%
Solution:
(d) 186%
(d) is correct
% Increase in price = 286 – 100 = 186%

Question 43.
What is the formula for calculating the deflated index:

Solution:
(c)

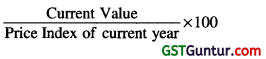
Question 44.
The index number for the year 2012 taking 2011 as base using simple average of price relatives method from data given below is: [1 Mark, Dec. 2013]

(a) 112
(b) 117
(c) 120
(d) 111
Solution:
(d) 111
P₀₁ = \(\frac{\sum p_1}{\sum p_0}\) × 100 = \(\frac{540}{488}\) × 100 = 110.65 = 1111

Question 45.
An index time series is a list of numbers for two or more periods of time
(a) Index
(b) absolute
(c) Relative
(d) None [1 Mark, Dec. 2013]
Solution:
(a) Index
(a) is correct.

Question 46.
Circular test is satisfied by which index number? [1 Mark, June 2014]
(a) Laspeyre’s
(b) Paasche’s
(c) Fisher’s
(d) None of the above
Solution:
(d) is correct
Note:- Circular test is satisfied by Simple Geometric mean of price Relatives and the aggregative with Fixed weights.

Question 47.
Fisher’s index number is ____ of Laspayre’s and Paasche’s index numbers [1 Mark, June 2014]
(a) A.M.
(b) G.M.
(c) H.M.
(d) None
Solution:
(b) G.M.
(b) is correct.

Question 48.
Which of the following statement is true ? [1 Mark, June 20]
(a) Paasche’s index number is based on base year quantity
(b) Fisher’s index satisfies the circular test
(c) Arithmetic mean is the most appropriate average for constructing the index number
(d) Splicing means constructing one continuous series from two different indices on the basis of common base
Solution:
(d) Splicing means constructing one continuous series from two different indices on the basis of common base
(d) is correct

Question 49.
Monthly salary of an employee was ₹ 10,000 in the year 2000 and it was increased to ₹ 20,000 in the year 2013 while the consumer price index number is 240 in year 2013 with the base year 2000, what should be his salary in comparison of consumer price index in the year 2013 ? [1 Mark, June 2014]
(a) 2,000
(b) 16,000
(c) 24,000
(d) None
Solution:
(c) 24,000
(c) is correct
p₀ = 10,000
Let Salary in yr. 2013 = p₁
∵ C.L.I = \(\frac{p_1}{p_0}\) × 100 ; or 240 = \(\frac{p_1}{10,000}\) × 100; ∴ p₁ = ₹ 24,000.

Question 50.
Σp₁q₀ = 1180, ΣP₀q₀ = 1170, Σp₁q₁ = 1064, Σp₀q₁ = 1100, then Fisher ideal index number is
(a) 96.73
(b) 98.795
(c) 98.77
(d) 100.86
Solution:
(c) 98.77
(c) is correct

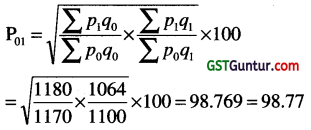
Question 51.
When the prices are decreased by 30% then the index number is now [1 Mark, Dec. 2014]
(a) 50
(b) 60
(c) 70
(d) 30
Solution:
(c) 70
(c) is correct
New I. No = . 100 – 30 = 70.

Question 52.
_____ play a very important role in the construction of index number. [1 Mark, June 2015]
(a) Weights
(b) Classes
(c) Estimate
(d) None
Solution:
(a) Weights
(a) is correct

Question 53.
Factor reversal test is
(a) \(\frac{\sum p_1 q_1}{\sum p_0 q_0}\)
(b) \(\frac{\sum p_1 q_1}{\sum p_0 q_0} \times \frac{\sum p_1 q_1}{\sum p_0 q_1}\)
(c) \(\frac{\sum p_1 q_1}{\sum p_0 q_1}\)
(d) \(\frac{\sum q_1 p_0}{\sum q_0 p_0} \times \frac{\sum q_1 p_1}{\sum q_0 p_1}\) [1 Mark, June 2015]
Solution:
(a) \(\frac{\sum p_1 q_1}{\sum p_0 q_0}\)
(a) is correct

Question 54.
If with a rise of 10% in prices the wages are increased by 20% the real wage increases by [1 Mark, June 2015]
(a) 10%
(b) More than 10%
(c) 20%
(d) Less than 10%
Solution:
(d) Less than 10%
(d) is correct
Real wage = \(\frac{100+20}{100+10}\) × 100 = 109.09
∴ Real wage increases by 9.09% i.e. less than 10%

Question 55.
Consumer Price index number for the year 1957 was 313 with 1940 as the base year. The Average Monthly wages in 1957 of the workers into factory be ₹ 160/- their real wages is: [1 Mark, Dec. 2015]
(a) ₹ 48.40
(b) ₹ 51.12
(c) ₹ 40.30
(d) None of these
Solution:
(b) ₹ 51.12
(b) is correct.
Real Wage = \(\frac{160}{313}\) × 100 = 51.12

Question 56.
Purchasing power of money is [1 Mark, June 2016]
(a) Reciprocal of price index number
(b) Equal to price index number
(c) Unequal to price index number
(d) None of these
Solution:
(a) Reciprocal of price index number

Question 57.
In the year 2010 the monthly salary was ₹ 24,000. The consumer price index number was 140 in the year 2010 which rises to 224 in the year 2016. If he has to be rightly compensated what additional monthly salary to be paid to him
(a) ₹ 14,400
(b) ₹ 38,400
(c) ₹ 7,200
(d) None of these
Solution:
(a) ₹ 14,400
∴ Additional monthly salary = 38400 – 24000 = ₹ 14,400/-

Question 58.
The suitable index numbers for the comparison of every year is
(a) Fixed base index number
(b) Fisher’s ideal index number
(c) Chain base index number
(d) Both (a) and (c)
Solution:
(c) Chain base index number

Question 59.
Index numbers are used in
(a) Economics
(b) Statistics
(c) Both (a) & (b)
(d) None
Solution:
(c) Both (a) & (b)
(c) is correct

Question 60.
From the following data [1 Mark, Dec. 2016]

The Paasche’s price index number is
(a) 146.41
(b) 148.25
(c) 144.25
(d) None
Solution:
(a) 146.41
(a) is correct.

Question 61.
The time reversal test is satisfied by ____ Index number. [1 Mark, Dec. 2016]
(a) Laspeyre’s
(b) Paasche’s
(c) Fisher’s
(d) None
Solution:
(c) Fisher’s
(c) is correct.

Question 62.
Fisher’s index number does not satisfy [1 Mark, June 2017]
(a) Unit test
(b) Circular test
(c) Time reversal test
(d) Factor reversal test
Solution:
(b) Circular test

Question 63.
If Laspeyre’s index is L and Paasche’s index is P then Fisher’s index F is [1 Mark, June 2017]
(a) F = L × P
(b) F² = L × P
(c) F² = \(\sqrt{L+P}\)
(d) F \(=\frac{1}{L \times P}\)
Solution:
(b) F² = L × P
F = \(\sqrt{\text { L.P }}\) ⇒ F² = L.P

Question 64.
The monthly income of aperson in the year 2014 was ₹8,000 and CPI was 160. The CPI is 200 in the year 2017. What will be the additional dearness allowance for the year 2017? [1 Mark, June 2017]
(a) 2400
(b) 2750
(c) 2500
(d) None
Solution:
(d) None
Monthly Income in 2017 = \(\frac{200}{100}\) × 8000 = ₹ 16,000
∴ DA = 16000 – 8000 = ₹ 8000

Question 65.
For knowing consumers price index number we want to collect data from : [1 Mark, Dec. 2017]
(a) Retail shop prices
(b) Wholesale shop prices
(c) Fair prices
(d) Government depots
Solution:
(a) Retail shop prices

Question 66.
The circular test is an extension of:
(a) The time reversal test
(b) The factor reversal test
(c) The unit test
(d) None of these
Solution:
(a) The time reversal test

Question 67.
Fisher’s ideal index number is :
(a) The arithmetic mean of Laspeyre’s and Paasche’s index
(b) The median of Laspeyre’s and Paasche’s index
(c) The mode of Laspeyre’s and Paasche’s index
(d) None of these
Solution:
(d) None of these

Question 68.
Price relative is equal to : [1 Mark, Dec. 2017]

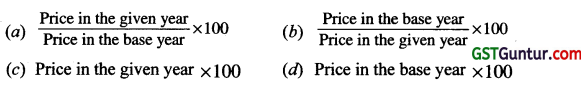
Solution:
(a)

Question 69.
GM of Laspeyre’s and Paasche’s Price Index number is price index number: [1 Mark, June 2018]
(a) Kelly’s
(b) Fisher’s
(c) Bowley’s
(d) None
Solution:
(b) Fisher’s

Question 70.
Paasche’s index number is expressed in terms of: [1 Mark, June 2018]
(a) \(\frac{\sum p_n q_n}{\sum p_o q_n}\)
(b) \(\frac{\sum p_o q_o}{\sum p_n q_n}\)
(c) \(\frac{\sum p_n q_n}{\sum p_o q_n} \times 100\)
(d) \(\frac{\sum p_n q_o}{\sum p_o q_o} \times 100\)
Solution:
(c) \(\frac{\sum p_n q_n}{\sum p_o q_n} \times 100\)

Question 71.
To overcome the disadvantage of a simple average of relative method, we can use ____:
(a) Weighted average of relative method
(b) Chain base index number
(c) Simple aggregative method
(d) Fixed base index number
Solution:
(a) Weighted average of relative method

Question 72.
Time reversal & factor reversal are : [1 Mark, May 2018]
(a) Quantity Index
(b) Ideal Index
(c) Price Index
(d) Test of consistency
Solution:
(d) Test of consistency

Question 73.
A series of numerical figures which show the relative position is called [1 Mark, May 2018]
(a) Index number
(b) Relative number
(c) Absolute number
(d) None
Solution:
(a) Index number

Question 74.
The number of test of Adequacy is [1 Mark, May 2018]
(a) 2
(b) 5
(c) 3
(d) 4
Solution:
(d) 4

Question 75.
P₀₁ is the index for time [1 Mark, May 2018]
(a) 1 on 0
(b) 0 on 1
(c) 1 on 1
(d) 0 on 0
Solution:
(a) 1 on 0
P₀₁ is the index number of 1 on 0.

Question 76.
The circular test is an extension of [1 Mark, May 2018]
(a) The time is reversal test
(b) The factor reversal test
(c) The unit test
(d) None of these
Solution:
(a) The time is reversal test

Question 77.
If ΣP₀Q₀ = 1360, ΣP_nQ₀ = 1900, ΣP₀Q_n = 1344, ΣP_nQ_n = 1880 then the Laspeyre’s Index Number is [1 Mark, May 2018]
(a) 0.71
(b) 1.39
(c) 1.75
(d) None of these
Solution:
(b) 1.39

Question 78.
Price Relative is expressed in term of
(a) P = \(\frac{\mathrm{P}_n}{\mathrm{P}_0}\)
(b) P = \(\frac{\mathrm{P}_0}{\mathrm{P}_n}\)
(c) P = \(\frac{\mathrm{P}_n}{\mathrm{P}_0} \times 100\)
(d) P = \(\frac{P_0}{P_n} \times 100\)
Solution:
(c) P = \(\frac{\mathrm{P}_n}{\mathrm{P}_0} \times 100\)
price Relative (P) = \(\frac{\mathrm{P}_n}{\mathrm{P}_0} \times 100\)

Question 79.
Circular test is satisfied by
(a) Laspeyre’s Index Number ‘
(b) Paasche’s Index Number
(c) The Simple Geometric Mean of Price Relatives and the Weighted Aggregative with fixed weights.
(d) None of these [1 Mark, May 2018]
Solution:
(c) The Simple Geometric Mean of Price Relatives and the Weighted Aggregative with fixed weights.

Question 80.
If the 1970 index with base 1965 is 200 and 1965 index with base 1960 is 150, the index 1970 on base 1960 will be : [1 Mark, May 2018]
(a) 700
(b) 300
(c) 500
(d) 600
Solution:
(b) 300

CBI = FBI = Index Number of 1970 on Base 1960 = 300
Note : – Chain Base Index Number =

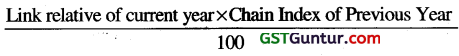
Question 81.
Which of the following statement is true? [1 Mark, Nov. 2018]
(a) Paasche’s Index Number is based on the base year quantity
(b) Fisher’s Index Number is the Arithmetic Mean of Laspeyre’s Index Number and Paasche’s Index Numbers
(c) Arithmetic Mean is the most appropriate average for constructing the index number
(d) Fisher’s Index Number is an Ideal Index Number
Solution:
(d) Fisher’s Index Number is an Ideal Index Number

Question 82.
If Laspeyre’s Index Number is 250 and Paasche’s Index Number is 160. Then Fisher’s index number is: [1 Mark, Nov. 2018]
(a) 40000
(b) \(\frac{25}{16}\)
(c) 200
(d) \(\frac{16}{25}\)
Solution:
(c) 200
Fisher’s I. No. = \(\sqrt{\mathrm{L} . \mathrm{P}}\) = \(\sqrt{250 \times 160}\) = 200

Question 83.
The simple average method is used to calculate: [1 Mark, Nov. 2018]
(a) Trend Variation
(b) Cyclical Variation
(c) Seasonal Variation
(d) Irregular Variation
Solution:
(c) Seasonal Variation

Question 84.
If ΣP₀Q₀ = 240, ΣP₁Q₁ = 480, ΣP₁Q₀ = 600, and ΣP₀Q₁ = 192, then Laspeyre’s Index Number is: [1 Mark, Nov. 2018]
(a) 250
(b) 300
(c) 350
(d) 200
Solution:
(a) 250
Laspeyre’s I. No. = \(\frac{\sum P_1 Q_1}{\sum P_0 Q_0} \times 100\)
= \(\frac{480}{192} \times 100\) = 250

Question 85.
Which one is called an ideal index number [1 Mark, June 2019]
(a) Laspeyre’s index number
(b) Paasche’s index number
(c) Fisher’s index number
(d) Marshall Edgeworth index number
Solution:
(c) Fisher’s index number

Question 86.
Which one is called an ideal index number
(a) Laspeyre’s index number
(b) Paasche’s index number
(c) Fisher’s index number
(d) Marshall Edgeworth index number [1 Mark, June 2019]
Solution:
(c) Fisher’s index number
Fisher’s Index No. is called an Ideal Index Number.

Question 87.
Which is not satisfied by Fisher’s Ideal index number ? [1 Mark, June 2019]
(a) Factor Reversal Test
(b) Time Reversal Test
(c) Circular Test
(d) None of the above
Solution:
(c) Circular Test

Question 88.
The prices and quantities of 3 commodities in base and current years are as follows :

The Laspeyre’s Price Index Number is [1 Mark, June 2019]
(a) 118.13
(b) 107.14
(c) 120.10
(d) None
Solution:
(b) 107.14
Here

Question 89.
The cost of living index numbers in years 2015 and 2018 were 97.5 and 115 respectively. The Salary of a worker in 2015 was ₹ 19500. How much additional salary was required for him in 2018 to maintain the Same standard of living as in 2015?
(a) 3000
(b) 4000
(c) 3500
(d) 4500
Solution:
(c) 3500
Here

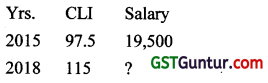
Salary Required in year 2018 \(=\frac{\text { CLI of } 2018}{\text { CLI of } 2015}\) × Salary in 2015
= \(\frac{115}{97.5}\) × 19500 = ₹ 23000
Addition Salary Required = 23,000 – 19,500 = ₹ 3,500