These Theoretical Distributions – CA Foundation Statistics Notes are designed strictly as per the latest syllabus and exam pattern.
Theoretical Distributions – CA Foundation Statistics Notes
Previous Year Exam Questions
Question 1.
Parameter is a characteristic of : [1 Mark, Nov. 2006]
(a) Population
(b) Sample
(c) Probability distribution
(d) Both (a) & (b)
Solution:
(a) Parameter :- A characteristic of a population.
Question 2.
What is the probability of making 3 correct guesses in 5 True – False answer type questions? [1 Mark, Nov. 2006]
(a) 0.4156
(b) 0.32
(c) 0.3125
(d) 0.5235
Solution:
(c) Here, Sample Space S = {True, False}
P = Probability of being (True) = 0.5, q = Prob. (False) = 0.5
Given that, n = 5, r = 3
P(X = 3) = 5C3(0.5)3(0.5)2 = 0.3125
![]()
Question 3.
The number of calls arriving at an internal switch board of an office is 96 per hour. Find the probability that there will be: [1 Mark, Feb. 2007]
(i) not more than 3 calls on the board,
(ii) at least four calls in a minute on the board. [Given: e-1.6 = 0.20 19]
(a) 0.08 and 0.92 respectively
(c) 0.92 and 0.13 respectively
(d) 0.92 & 0.08 respectively
Solution:
(d) Let X be the No. of calls on board. Therefore, No. of calls per hour. = 96
⇒ m= \(\frac{96}{60}\) = 1.6 = No. of calls per minute
(i) P(X < 3) = P(X = 0) + P(X = 1) +P(X = 2) + P(X = 3)
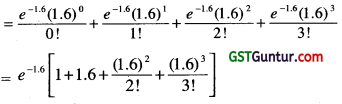
= 0.2019 × 4.56 = 0.920
(ii) = 1 – 0.92 = 0.08
Question 4.
The probability density function of a normal variable x is given by: [1 Mark, Feb. 2007]
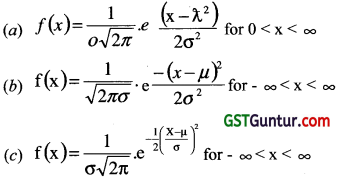
(d) None of these
Solution:
(c) is correct.
Question 5.
The Interval (μ – 3σ, μ + 3σ) covers [1 Mark, May 2007]
(a) 95% area of normal distribution
(b) 96% area of normal distribution
(c) 99% area of normal distribution
(d) All but not 0.27% area of a normal distribution
Solution:
(d) 99.73 % of the value of a normal variates lies between (μ – 3σ) and (μ + 3σ). Hence, the interval (μ – 3σ, μ + 3σ) covers all but not 100- 99.73 % – 0.27% area of a normal distribution.
![]()
Question 6.
The overall percentage of failure in a certain examination is 0.30. What is the probability that out of a group of 6 candidates at least 4 passed the examination? [1 Mark, May 2007]
(a) 0.74
(b) 0.71
(c) 0.59
(d) 0.67
Solution:
(a) Given that p = probability of success and q = probability of failure
∴ p = 0.70, q = 0.30
Probability that at least 4 candidates passed the examination i.e.
p (X ≥ 4) = 6C4(0.7)4(0.3)2 + 6C5(0.7)5(0.3)1 + 6C6(0.7)6(0.3)0
= 0.74 [Do these with calculator.]
Question 7.
A manufacturer, who produces medicine bottles, finds that 0.1 % of the bottles are defective. The bottles are packed in boxes containing 500 bottles. A drug manufacturer buys 100 boxes from the producer of bottles. Using Poisson distribution, find how many boxes will contains at least two defectives: [Given: e-05 = 0.6065] [1 Mark, May 2007]
(a) 7
(b) 13
(c) 9
(d) 11
Solution:
(c) Given that n = 500 and p = \(\frac{0.1}{100}\) = 0.001
So, m = n p = 500 × 0.001 = 0.5; Where m = mean; n = No. of bottles
P(X ≥ 2) = 1 – P(X < 2)
= 1 – [P(X = 0) + P(X =1)]
= 1 – \(\left[\frac{e^{-0.5}(0.5)^0}{0 !}+\frac{e^{-0.5}(0.5)^1}{1 !}\right]\)
= 1 – [0.6065 + 0.5 × 0.6065] = 1 – 0.9097 = 0.0902
(∴ Given e-0.5 = 0.6065)
Hence, the approx, number of boxes containing at least 2 defective bottles.
= N . P (x > 2)
= 100 × P(X ≥ 2) = 100 × 0.0902 = 9, (approx.)
![]()
Question 8.
The number of methods of fitting the normal curve is: [1 Mark, Aug. 2007]
(a) 4
(b) 3
(c) 2
(d) 1
Solution:
(c) There are 2 methods of fitting the normal curve which are.
(i) Ordinate method
(ii) Area method
Question 9.
Suppose that weather records show that on an average 5 out of 31 days in October are rainy days. Assuming a binomial distribution with each day of October as an independent trial, then the probability that the next October will have at most three rainy days is : [1 Mark, Aug. 2007]
(a) 0.4403
(b) 0.2403
(c) 0.3403
(d) None
Solution:
(b) p = Probability of a rainy day in October = 5/31;
q = probability of a non – rainy day in October
∴ q = 1 – P ; ∴ q = 1 – \(\frac{5}{31}\) = \(\frac{26}{31}\)
Since , n = 31 ( Number of days in October )
P(X = r) = 31Cr \(\left(\frac{5}{31}\right)^r\left(\frac{26}{31}\right)^{31-r}\)
Required Probability = P(0) + P(1) + P(2) +P(3)
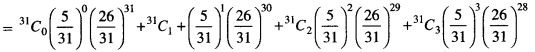
= 0.2403 [Note : Here use calculator in calculation.]
![]()
Question 10.
If 5% of the families in Kolkata do not use gas as a fuel, what will be the probability of selecting 10 families in a random sample of 100 families who do not use gas as fuel ? [Given: e-5 = 0.0067] [1 Mark, Aug. 2007]
(a) 0.038
(b) 0.028
(c) 0.048
(d) 0.018
Solution:
(d) Given, P = 5% = 0.05 = P (families who do not use gas as fuel)
No. of families n = 100
∴ Mean = m = np = 100 × 0.05 = 5
∴ Probability of selecting 10 families.
P(X = 10) = \(\frac{\mathrm{e}^{-5}(5)^{10}}{10}\) (Given e-5 = 0.0067)
= \(\frac{0.0067 .(5)^{10}}{10 !}\) = 0.018
Question 11.
If 15 dates are selected at random, then the probability of getting two Sundays is: [1 Mark, Nov. 2007]
(a) 0.29
(b) 0.99
(c) 0.49
(d) 0.39
Solution:
(a) Let p = Probability of getting a Sunday in a week
∴ P = \(\frac{1}{7}\) and q = 1 – P = \(\frac{6}{7}\)
So, required probability
P(X = 2)= 15C2\(\left(\frac{1}{7}\right)^2\left(\frac{6}{7}\right)^{13}\) = 0.288 ≈ 0.29
![]()
Question 12.
If X is a Poisson variate with P (X = 0) = P (X = 1), then P (X = 2) = ? [1 Mark, Nov. 2007]
(a) \(\frac{1}{6 e}\)
(b) \(\frac{e}{6}\)
(c) \(\frac{1}{2 e}\)
(d) \(\frac{e}{3}\)
Solution:
(c)
Given that, P(X = 0) = P(X = 1)
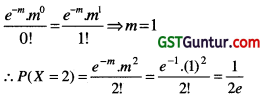
Question 13.
In a certain manufacturing process, 5% of the tools produced turn out to be defective. Find the probability that in a sample of 40 tools, at most 2 will be defective: [Given: e-2 = 0.135] [1 Mark, Feb. 2008]
(a) 0.555
(b) 0.932
(c) 0.785
(d) 0.675
Solution:
(d) Given, n = 40 tools and p = probability of defective tools = 0.05, mean = m (let)
∴ m = np = 40 × 0.05 = 2
So, P(at most 2 defective tools)
P(X ≤ 2) = P(X = 0) + P(X = 1) + p(X = 2)
= \(\frac{e^{-2} \cdot(2)^0}{0 !}+\frac{e^{-2} \cdot(2)^1}{1 !}+\frac{e^{-2} \cdot(2)^2}{2 !}\) = e-2[1 + 2 + 2] = 0.135 × 5 = 0.675
![]()
Question 14.
Examine the validity of the following: [1 Mark, Feb. 2008]
Mean and standard Deviation of a binomial distribution are 10 and 4 respectively.
(a) Not valid
(b) Valid
(c) Both (a) & (b)
(d) Neither (a) nor (b)
Solution:
(a)
Formula, Mean = np = 10, σ = \(\sqrt{n p q}\) = 4
So, n p = 10 & n p q = 16
⇒ 10 . q = 16
∴ q = 1.6 > 1 (not possible) because probability always lies from 0 to 1.
Question 15.
An experiment succeeds twice as often as it fails. What is the probability that in next five trials there will be at least three successes? [1 Mark, June 2008]
(a) \(\frac{33}{81}\)
(b) \(\frac{46}{81}\)
(c) \(\frac{64}{81}\)
(d) \(\frac{25}{81}\)
Solution:
(c) Given statement is
p = 2q
∵ p + q = 1
∴ 2q + q = 1;⇒ 3q = 1 ⇒ q = \(\frac{1}{3}\)
∴ p = \(\frac{2}{3}\) , q = \(\frac{1}{3}\)
Required probability:
P(x ≥ 3) = p(x = 3) + p(x = 4) + p(x = 5)
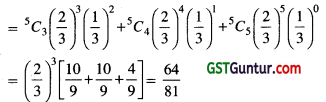
Question 16.
The probability than a man aged 45 years will die within a year is 0.012. What is the probability that of 10 men, at Least 9 will reach their 46th birthday? [Given: e-0.12 = 0.88692] [1 Mark, June 2008]
(a) 0.0935
(b) 0.9934
(c) 0.9335
(d) 0.9555
Solution:
(b) Given that p = 0.012 and n = 10
∴ m = np = 10 × 0.012 = 0.12
Hence, P (at least 9 men will celebrate their 46th birthday)
= P (if 9 men survive means 1 will die and if all 10 men survive means 0 person will die)
= p(X = 0) + p(x = 1)
= \(\frac{e^{-0.12} \cdot(.12)^0}{0 !}+\frac{e^{-0.12} \cdot(.12)^1}{1 !}\) = e-0.12[1 + 0.12] = 0.88692 × 1.12 = 0.9934
![]()
Question 17.
In Poisson Distribution, probability of success is very close to : [1 Mark, June 2008]
(a) -1
(b) 0
(c) 1
(d) None
Solution:
(b)
Question 18.
If x and y are two independent standard normal variables, then the distribution of \(\frac{\mathrm{x}}{\mathrm{y}}\) is : [1 Mark, Dec. 2008]
(a) Normal Distribution
(b) Exponential Distribution
(c) Couchy’s Distribution
(d) Binomial Distribution
Solution:
(a)
Question 19.
If the mean of a poisson variable X is 1, what is P (x = at least one)? [1 Mark, Dec. 2008]
(a) 0,456
(b) 0.821
(c) 0.632
(d) 0.254
Solution:
(c)
Given, Mean m = 1
We have to find P(X ≥ 1) = 1 – P(X < 1)
= 1 – P(X = 0) = 1 – \(\frac{e^{-1} \cdot(1)^0}{0 !}\) = 1 – \(\frac{1}{e}\) = 1 -0.3679; (as e = 2.7183)
= 0.0632
![]()
Question 20.
What is the probability of getting 3 heads if 6 unbiased coins are tossed simultaneously ? [1 Mark, Dec. 2008]
(a) 0.3125
(b) 0.25
(c) 0.6875
(d) 0.50
Solution:
(a)
Given, n = 6 = No. of tossings,
p = Prob. of getting head in a trial. = 1/2
q = 1 – p = 1 – 1/2 = 1/2
So, f (X = 3) = 6C3 (1 / 2)3 (1 / 2)3
= 20 × \(\left(\frac{1}{2}\right)^6\) = 0.3125
Question 21.
Shape of Normal Distribution Curve: [1 Mark, Dec. 2009]
(a) Depends on its parameters
(b) Does not depend on its parameters
(c) Either (a) or (b)
(d) Neither (a) nor (b)
Solution:
(a)
![]()
Question 22.
For binomial distribution E(x) = 2, V(x) = 4/3. Find the value of n. [1 Mark, Dec. 2009]
(a) 3
(b) 4
(c) 5
(d) 6
Solution:
(d).
E(X) = np = 2 ; v(x) = npq = 4/3
⇒ 2q = \(\frac{4}{3}\) ⇒ q = \(\frac{4}{3 \times 2}\) = \(\frac{2}{3}\)
∴ q = \(\frac{2}{3}\)
Now p = 1 – q = 1 – \(\frac{2}{3}\) = \(\frac{1}{3}\)
Since, np = 2 ⇒ n × \(\frac{1}{3}\) = 2
∴ n = 6.
Question 23.
What are the parameters of binomial distribution ? [1 Mark, Dec. 2009]
(a) n
(b) p
(c) Both n and p
(d) None of these
Solution:
(c) Binomial Distribution is a bi-parametric distribution i.e. ‘n’ and ‘p’
![]()
Question 24.
The Variance of standard normal distribution is ________ [1 Mark, June 2010]
(a) 1
(b) μ
(c) σ2
(d) 0
Solution:
(c)
Question 25.
In Binomial distribution, n = 9 and P = 1/3 what is the value of variance: [1 Mark, June 2010]
(a) 8
(b) 4
(c) 2
(d) 16
Solution:
(c) q = 1 – p = 1 – 1/3 = 2/ 3
So, Variance = npq = 9 . \(\frac{1}{3}\) . \(\frac{2}{3}\) = 2
Question 26.
If standard deviation of a poisson distribution is 2 , then its [1 Mark, Dec. 2010]
(a) Mode is 2
(b) Mode is 4
(c) Modes are 3 and 4
(d) Modes are 4 and 5
Solution:
(c) ∵ S.D = 2 ⇒ Variance = σ2 =4
∵ In poisson distribution, Mean = variance = 4 (Integer)
So; it is bi-modal
∴ Modes are m and (m – 1)
i.e., Mo = 4 and 3,
![]()
Question 27.
The area under the Normal curve is [1 Mark, Dec. 2010]
(a) 1
(b) 0
(c) 0.5
(d) -1
Solution:
(a)
Question 28.
For a normal distribution N (µ, σ2), P(µ – 3σ < x < µ + 3σ) is equal to [1 Mark, Dec. 2010]
(a) 0.9973
(b) 0.9546
(c) 0.9899
(d) 0.9788
Solution:
(a)
∵ Area in P(µ – 36 < x < µ + 36) = 0.9973
Question 29.
If for a Binomial distribution B (n, p) the mean = 6 and Variance = 2 then ‘p’ is [1 Mark, Dec. 2010]
(a) 2/3
(b) 1/3
(c) 3/5
(d) 1/4
Solution:
(a) Mean = 6 = np
& Variance = 2 – npq ⇒ 6q = 2 ⇒ q = 1 / 3
So, p = 1 – q = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\) ⇒ p = \(\frac{2}{3}\)
![]()
Question 30.
If the inflexion points of a Normal Distribution are 6 and 14. Find its Standard Deviation? [1 Mark, June 2011]
(a) 4
(b) 6
(c) 10
(d) 12
Solution:
(a)
Upper point of inflexion = μ + σ = 14 ………… (i)
& Lower point of inflexion = μ – σ = 6 ………….. (ii)
Eqn . (i) – (ii), we get
2 σ = 14 – 6 = 8; So, σ = 4
Hence, S.D (σ) =4
Question 31.
In a Binomial Distribution, if mean is k-times the variance, then the value of ‘k’ will be _______. [1 Mark, June 2011]
(a) P
(b) q
(c) 1 – p
(d) \(\frac{1}{1-\mathrm{P}}\)
Solution:
(d)
We know that in Binomial Distribution:
Mean = np & Variance = npq
From question
Mean = k(Variance) ⇒ np = K.(npq) ⇒ kq = 1 .
∴ K = 1/q ∴ K = \(\frac{1}{1-\mathrm{P}}\)
![]()
Question 32.
The mean of Binomial distribution is 20 and Standard deviation is 4 then; [1 Mark, Dec. 2011]
(a) n = 100, p = 1/5, q = 4/5
(b) n = 50, p = 2/5, q = 2/5
(c) n = 100, p = 2/5, q = 4/5
(d) n = 100, p = 1/5, q = 3/5
Solution:
(a)
Given, Mean = 20 ; S.D = 4
⇒ np = 20; Variance = npq = (4)2
⇒ npq =16
⇒ 20q = 16; q = \(\frac{4}{5}\)
Hence p = 1 – q = 1 – \(\frac{4}{5}\); p = \(\frac{1}{5}\)
So, np = n × \(\frac{1}{5}\) = 20 ⇒ n = 20 × 5 = 100
Question 33.
A Company has two cars which it hires out during the day. The number of Cars demanded with mean 1.5. Then percentage of days on which only one car was in demand is equal to [1 Mark, Dec. 2011]
(a) 23.26
(b) 33.47
(c) 44.62
(d) 46.40
[Given Exp. (-1.5) = 0.2231]
Solution:
(b)
Given; mean = m = 1.5
Formula, P(x) = \(\frac{\mathrm{e}^{-\mathrm{m}} \cdot \mathrm{m}^{\mathrm{x}}}{\mathrm{x} !}\)
So, P(X = 1) = \(\frac{e^{-1.5} \cdot(1.5)^1}{1 . !}=\frac{0.2231 \times 1.5}{1}\)
= 0.33465 = 0.3347 = 33.47 %
![]()
Question 34.
The binomial distribution with mean 3 & variance 2 is: [1 Mark, Dec. 2011]

Solution:
(c) Given mean np = 3
Variance npq = 2
3q = 2 ; So, q = 2/3 ; Hence p = 1 – \(\frac{2}{3}\) = \(\frac{1}{3}\)
Since, np = n × \(\frac{1}{3}\) = 3 ; So, n = 9
The binomial distribution is (q + p)n = [\(\frac{2}{3}\) + \(\frac{1}{3}\)]9
Question 35.
For binomial distribution [1 Mark, June 2012]
(a) Variance Mean
(d) None of the above
Solution:
(a) For Binomial distribution
npq < np ⇒ Variance < Mean
Question 36.
If X is a Poisson variate and E(x) = 1, then P (x > 1) is [1 Mark, June 2012]
(a) 1 – \(\frac{e^{-1}}{2}\)
(b) 1 – e-1
(c) 1 – 2e-1
(d) 1 – \(\frac{5}{2}\)e
Solution:
(c) Since, P(x) = \(\frac{e^{-m} m^x}{x !}\) ; E(X) = m= 1 = mean
∴ P(x > 1) = 1 – P(x < 1)
= 1 – [P(x = 0)+ P(X = 1)]
= 1 – \(\left[\frac{\mathrm{e}^{-1} \cdot 1^0}{0 !}+\frac{\mathrm{e}^{-1} \cdot 1^1}{1 !}\right]\)
=1 – [e-1 + e-1] = 1 – 2e-1
![]()
Question 37.
The mean and the variance of a random variable X having the probability density function P(X = x) = exp. {- (x – 4)2}/ \(\sqrt{\pi}\), -∞ < x < ∞ is v
(a) 4, \(\frac{1}{2}\)
(b) 4, \(\frac{1}{\sqrt{2}}\)
(c) 2, 2
(d) 2, \(\frac{1}{2}\)
Solution:
(a) Normal distribution – density function is:
P(X = x) = \(\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-\mu)^2}{\sigma}\right)^2}\) , -∞< X < ∞
Given equation:
P(X = x) = \(\frac{1}{\sqrt{\pi}}\) e-(x-4)2 = \(\frac{1}{\frac{1}{\sqrt{2}} \sqrt{2 \pi}} \cdot e^{-\frac{1}{2}\left(\frac{x-4}{1 / \sqrt{2}}\right)^2}\)
Comparing given function with the standard form, we get Mean (u) = 4
S.D (σ) = \(\frac{1}{\sqrt{2}}\)
∴ Variance(σ2)= \(\frac{1}{2}\)
Question 38.
In a Normal Distribution [1 Mark, Dec. 2012]
(a) The first and second quartile are equidistant from median
(b) The second and third quartiles are equidistant from the median
(c) The first and third quartiles are equidistant from the median
(d) None of the above
Solution:
(c) In a Normal Distribution :
“ The first and third quartiles are equidistant from the median”.
![]()
Question 39.
If a parameters of a binomial distribution are n and p then, this distribution tends to a poisson distribution when [1 Mark, Dec. 2012]
(a) n → ∞, p → 0
(b) p → 0, np = λ
(c) p → ∞, np = λ
(d) n → ∞, p → 0, np = λ.
where ’λ’ is a finite constant
Solution:
(d)
Question 40.
If a random variable x follows Poisson distribution such that E(x) = 30, then the variance of the distribution is [1 Mark, Dec. 2012]
(a) 7
(b) 5
(c) 30
(d) 20
Solution:
(c) In Poisson distribution,
Mean = Variance
E(X) = 30 = Mean ; So, Variance = 30
![]()
Question 41.
In a normal distribution quartile deviation is 6 the standard deviation will be [1 Mark, Dec. 2012]
(a) 4
(b) 9
(c) 7.5
(d) 6
Solution:
(b) In Normal distribution
4 S D. = 6. Q.D.
S.D. = \(\frac{6}{4}\) Q.D. = \(\frac{6}{4}\) × 6 = 9
Question 42.
Which of the following is false in case of Normal distribution. [1 Mark, June 2013]
(a) it is multi model
(b) mean = median = mode
(c) it is symmetric
(d) Total area is 1
Solution:
(a) No ; it is uni-modal not multi-modal.
![]()
Question 43.
If x ~ B (5, p) and p(x = 2) = 0.4362 and p (x = 3) = 0.2181 then p = …………… [1 Mark, June 2013]
(a) 3/4
(b) 1/3
(c) 2/3
(d) 1/4
Solution:
(b) is correct
Given; n= 5
P(X = 2) = 5C2.p2q3 = 10.p2q3 = 0.4362 ………………… (1)
P(X = 3) = 5C3.P3q2 = 0.2181
10 p3q2 = 0.2181 ……………….. (2)
Eqn.(1) ÷ (2); We get
\(\frac{10 p^2 q^3}{10 p^3 q^2}\) = 2 ; or \(\frac{q}{p}\) = 2 ; or 2p = q
or 2p = 1 – p ; or 2p + p = 1 ; or p = \(\frac{1}{3}\)
Question 44.
In a poisson distribution [1 Mark, June 2013]
(a) Mean & SD are equal
(b) Mean,variance are equal
(c) SD & variance are equal
(d) both (a) and (b)
Solution:
(b) Mean = Variance.
![]()
Question 45.
In Binomial Distribution, μ = 4 and σ2 = 3 then mode = ……………….. [1 Mark, June 2013]
(a) 4
(b) 4.25
(c) 4.5
(d) 4.1
Solution:
(a) is correct.
Since, Mean = np = 4 & npq = 3 (Given)
So, 3 q = 4; So, q = 3 / 4 & p = 1 – q = 1/4
n.(1/4 ) = 4 ; Hence n = 16
Now, (n + 1)p = (16 + 1 ) (1/4) = 4.25
Rule : Mo = The integral part of (n + 1)p = 4.25 = 4 ; So , Mo = 4
Question 46.
In Normal distribution mean median and mode are [1 Mark, Dec. 2013]
(a) Equal
(b) Not equal
(c) Zero
(d) None of the above
Solution:
(a) is correct.
![]()
Question 47.
If the points of inflexion of a normal curve are 6 and 14 then standard deviation is [1 Mark, Dec. 2013]
(a) 4
(b) 8
(c) 16
(d) 32
Solution:
(a) is correct.
Given that, Lower point of inflexion = μ – σ = 6 …………… (i)
Upper point of inflexion = μ + σ = 14 ……………… (ii)
Eqn. (ii) – (i); we get
2σ = 8
σ = 4
Question 48.
There are 75 students in a class and their average marks is 50 and S .D of marks is 5. Number of students who have secured more than 60 marks (Given that area under the normal curve for Z = 2 is 0.4772) is ____________ [1 Mark, Dec. 2013]
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b) is correct
Given N = 75 ;
Mean = μ = 50; SD = σ = 5
Z at x = 60 = \(\frac{X-\mu}{\sigma}=\frac{60-50}{5}\) = 2
a 5 P(X > 60) = P(z > 2) = 0.5 – p(0 ≤ z ≤ 2)
= 0.5 – 0.4772 = 0.0228
Total No. of students scoring more than 60 marks = N.P(x > 60)
= 75 × 0.0228 = 1.71 = 2
![]()
Question 49.
If a variate X has, Mean > variance, then its distribution will be [1 Mark, June 2014]
(a) Binomial
(b) Posisson
(c) Normal
(d) t-distribution
Solution:
(a) is correct
Note : np > npq : Mean > Variance
Question 50.
Mean & variance of a Binomial variate are 4 and \(\frac{4}{3}\) respectively then P(x ≥ 1) will be ________ [1 Mark, June 2014]
(a) \(\frac{728}{729}\)
(b) \(\frac{1}{729}\)
(c) \(\frac{723}{729}\)
(d) None
Solution:
(a) is correct
Mean = np = 4 ; Variance = npq = \(\frac{4}{3}\)
or 4q = \(\frac{4}{3}\) ; or, q = \(\frac{1}{3}\)
p = 1 – q = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
Since , np = 4 ; So, n . \(\frac{2}{3}\) = 4 or n = 6
∴ P(X ≥ 1) = 1 – p(X < 1)
= 1 – P(x = 0)
= 1 – 6C0 . p0.q6
= 1 – 1 . 1 . (1/3)6 = 1 – \(\frac{1}{729}\)
= \(\frac{728}{729}\) N
![]()
Question 51.
5,000 students were appeared in an examination. The mean of marks was 39.5 with standard deviation 12.5 marks. Assuming the distribution to be normal,find the number of students recorded more than 60% marks. [Given when Z = 1.64 area of normal curve = 0.4494] [1 Mark, June 2014]
(a) 1000
(b) 505
(c) 253
(d) 2227
Solution:
(c) is correct
Given μ, = 39.5 ; σ = 12.5
Z at x = 60 = \(\frac{X-\mu}{\sigma}\) = \(\frac{60-39.5}{12.5}\) = 1.64
P(X > 60%) = 0.5 – p(39.5 ≤ X ≤ 60)
0.5 – p(0 ≤ z ≤ 1.64)
= 0.5 – 0.4494 = 0.0506
No. of students scoring more than 5,000 students = N.P (x > 60%)
= 5000 × 0.0506 = 253
![]()
Question 52.
Let the distribution function of a random variable x be F(x) = P(x ≤ x),then F(5) – F(2) [1 Mark, Dec. 2014]
(a) P(2 ≤ x < 5)
(b) P(2 ≤ x ≤ 5)
(c) P(2 ≤ x ≤ 5)
(d) P(2 < x < 5)
Solution:
(b) is correct
F(5) – F(2)
=p(0 ≤ x ≤ 5) – p(0 ≤ x ≤ 2)
= p(2< x ≤ 5).
Question 53.
For a Binomial distribution mean is 4 and variance is 3 then, 3rd central moment is _____________ [1 Mark, Dec. 201 4]
(a) 5/2
(b) 7/4
(c) 3/2
(d) 1/3
Solution:
(c) is correct
np = 4; npq = 3
∴ 4q = 3 ⇒ q = \(\frac{3}{4}\); p = 1 – q = 1 – \(\frac{3}{4}\) = \(\frac{1}{4}\)
Formula; 3rd Central Moment μ3 = npq(q – p) =
= 3(\(\frac{3}{4}\) – \(\frac{1}{4}\)) = 3 × \(\frac{2}{4}\) = \(\frac{3}{2}\)
![]()
Question 54.
In a Normal distribution mean =2 and variance =4 then, 4th central moment is ____________ [1 Mark, Dec. 2014]
(a) 16
(b) 32
(c) 48
(d) 64
Solution:
Mean = 2; var. = σ2 = 4
Formula ; 4th Central Moment = μ4 = 3.σ4 = 3.(σ2)2 = 3 × 42 = 48
Question 55.
X and Y are two independent Normal variables, then the distribution of x + y is __________ [1 Mark, Dec. 2014]
(a) Normal distribution
(b) t-distribution
(c) Chi-Square distribution
(d) F-distribution
Solution:
(a) is correct.
X and Y are two independent variables which follows Normal-distribution
∴ x + y also follows Normal distribution.
![]()
Question 56.
In the Binomial distribution the parameters are n and p, then X assumes values [1 Mark, June 2015]
(a) Between 0 and n
(b) Between 0 and n both inclusive
(c) Between 0 and 1
(d) Between 0 and ∞
Solution:
(b) is correct.
P(x = r) = nCr . pr . qn-r
Where r = 0, 1, 2 , ………..; n
Question 57.
In ___________ distribution, Mean = Variance [1 Mark, June 2015]
(a) Binomial
(b) Poisson
(c) Normal
(d) None
Solution:
(b) is correct.
![]()
Question 58.
Under normal curve μ ± 3σ covers _________ of the area of items. [1 Mark, June 2015]
(a) 100%
(b) 99%
(c) 99.73%
(d) 99.37%
Solution:
(c) is correct.
Question 59.
Wages paid to workers follows [1 Mark, Dec. 2015]
(a) Binominal distribution
(b) Poisson distribution
(c) Normal
(d) Chi-Square
Solution:
(c) is correct.
Question 60.
For a Binominal distribution, the parameters are 15 and 1/3 Find mode: [1 Mark, Dec. 2015]
(a) 5 and 6
(b) 5.5
(c) 5
(d) 6
Solution:
(c) is correct.
Given n = 15 ; p = \(\frac{1}{3}\)
∴ Mode = Integral part of (n +1 )p – (15 + 1)\(\frac{1}{3}\) = 5.33
∴ Mo = 5
Question 61.
Standard Deviation of Binominal distribution is – [1 Mark, Dec. 2015]
(a) npq
(b) (npq)2
(c) \(\sqrt{n p q}\)
(d) n2p2q2
Solution:
(c) is correct.
![]()
Question 62.
The Normal curve is _____________ [1 Mark, June 2016]
(a) Positively skewed
(b) Negatively skewed
(c) Symmetrical
(d) All these
Solution:
(c) is correct.
Question 63.
For a poisson variate X, P(X = 1) = P(X = 2). What is the mean of X ? [1 Mark, June 2016]
(a) 1
(b) 3/2
(c) 2
(d) 5/2
Solution:
(c)
∴ P(X = 1)= P(X = 2)
\(\frac{m^1 \cdot e^{-m}}{1 !}=\frac{m^2 \cdot e^{-m}}{2 !}\) ⇒ 1 = \(\frac{m}{2}\)
∴ m = 2
So, m = mean of x = 2
Question 64.
In _________ distribution mean = variance. [1 Mark, Dec. 2016]
(a) Binomial
(b) Normal
(c) Poisson
(d) t
Solution:
(c) is correct.
![]()
Question 65.
__________ is/are Bi-parametric distribution(s) [1 Mark, Dec. 2016]
(a) Binomial
(b) Poisson
(c) Normal
(d) Both (a) & (c)
Solution:
(d) correct.
Question 66.
In Poisson distribution μ4 = 2, then find μ2. [1 Mark, Dec. 2016]
(a) 2
(b) 4
(c) \(\frac{2}{3}\)
(d) \(\frac{1}{2}\)
Solution:
(c) correct
∵ Fourth moment of poisson – Distribution
μ4 = 3μ2
2 = 3σ2
∴ σ2 = \(\frac{2}{3}\)
![]()
Question 67.
The second & third moments of observations (-6, -4, -2, 0, 2, 4, 6) are ________ [1 Mark, Dec. 2016]
(a) (12, 0)
(b) (0,12)
(c) (16, 0)
(d) (0,16)
Solution:
(c) is correct;
μ2 = \(\frac{\sum(x-\bar{X})^2}{N}\) = σ2 = 16;
μ3 = 0 (Always)
Question 68.
If X & Y are two independent Normal variates with means μ1 and μ2 and standard deviations σ1 & σ2 respectively, then X + Y follows _________ [1 Mark, Dec. 2016]
(a) Mean = μ1 + μ2, S.D = 0
(b) Mean = μ1 + μ2, S.D = σ12 + σ22
(c) Mean = 0, S.D = σ12 + σ22
(d) Mean = μ1 + μ2, S.D = \(\sqrt{\sigma_1^2+\sigma_2^2}\)
Solution:
(d) is correct.
![]()
Question 69.
In ____________ distribution, mean = variance. [1 Mark, June 2017]
(a) Binomial
(b) Poisson
(c) Normal
(d) None
Solution:
(b)
Question 70.
In Binomial distribution, if variance = mean2 then n & p are : ________ [1 Mark, June 2017]
(a) 1, \(\frac{1}{2}\)
(b) 1, 1
(c) 2, \(\frac{1}{2}\)
(d) 3, \(\frac{1}{2}\)
Solution:
(a) is correct
Tricks : GBC.
Mean = np = 1 . \(\frac{1}{2}\) = \(\frac{1}{2}\)
Var. = npq = 1 . \(\frac{1}{2}\) . (\(\frac{1}{2}\)) = (mean)2
![]()
Question 71.
If X ~ N (50, 16) then which of the following is not possible. [1 Mark, June 2017]
(a) P(X > 60) = 0.30
(b) P(X < 50) = 0.50
(c) P(X < 60) = 0.40 (d) P(X > 50) = 0.50
Solution:
(c)
for (c)
P (x < 60) = P (x < 50)+ P (50 ≤ x ≤ 60)
= 0.0.5 + P (50 ≤ x ≤ 60)
definitely greater than 50%.
∴ (c) not possible.
Question 72.
The distribution of demand is as follows: [1 Mark, Dec. 2017]

The mean is given by
(a) 7.55
(b) 7.85
(c) 1.25
(d) 8.35
Solution:
(a) Mean = Σ Px
= 5 (0.05) + 6 (0.1) + 7 (0.3) + 8 (0.4) + 9(0.1) +10(0.05)
= 7.55
![]()
Question 73.
In __________ distribution, mean = variance : [1 Mark, Dec. 2017]
(a) Binomial
(b) Poisson
(c) Normal
(d) None of these
Solution:
(b)
Question 74.
An example of a bi-parametric discrete probability distribution is : [1 Mark, Dec. 2017]
(a) Binomial distribution
(b) Poisson distribution
(c) Normal distribution
(d) Both (a) & (b)
Solution:
(a)
![]()
Question 75.
InNormal distribution 95% observation lies between _________ & _________ : [1 Mark, Dec. 2017]
(a) (μ – 2σ , μ + 2σ )
(b) (μ – 3σ , μ + 3σ )
(c) (μ – 1.96o, μ + 1.96σ )
(d) (μ – 2.58o, μ +2.58σ )
Solution:
(c)
Question 76.
If x is a poisson variate with mean m then z = \(\frac{x-m}{\sqrt{m}}\) follows _________ distribution: [1 Mark, June 2018]
(a) Normal
(b) Binomial
(c) Bernoulli
(d) None of the above
Solution:
(a)
![]()
Question 77.
The mean of a Binomial distribution is ___________: [1 Mark, June 2018]
(a) np(1 – p)
(b) np
(c) \(\sqrt[n]{p(1-p)}\)
(d) None of the above
Solution:
(b)
Question 78.
Mean of poisson distribution is 6 then variance is __________: [1 Mark, June 2018]
(a) 6
(b) \(\sqrt{6}\)
(c) 4
(d) 3
Solution:
(a)
Question 79.
For a Poisson variate X, P(X = 2) = 3P (X = 4), then the standard deviation of X is _________ [1 Mark, Nov. 2018]
(a) \(\sqrt{2}\)
(b) 3
(c) 4
(d) 5
Solution:
(a)
∵ P(X = 2) = 3 P(X = 4)
or ; \(\frac{\mathrm{m}^2 \cdot e^{-\mathrm{m}}}{2 !}\) = 3 . \(\frac{\mathrm{m}^4 \cdot e^{-\mathrm{m}}}{4 !}\)
⇒ \(\frac{1}{2}\) = \(\frac{3 \cdot \mathrm{m}^2}{24}\)
or m2 = 4 ⇒ m = 2
∴ Var. m = σ2 = 2
σ = \(\sqrt{2}\)
![]()
Question 80.
The mean of the Binomial distribution B(4, \(\frac{1}{3}\)) is equal to _________ [1 Mark, Nov. 2018]
(a) \(\frac{3}{5}\)
(b) \(\frac{4}{3}\)
(c) \(\frac{8}{3}\)
(d) \(\frac{3}{4}\)
Solution:
(b)
Given; n = 4; P = \(\frac{1}{3}\);
Mean = np = 4 . \(\frac{1}{3}\) = \(\frac{4}{3}\)
Question 81.
If for a Normal-distribution Q1 = 54.52 and Q2 = 78.86, then the median of the distribution is ________ [1 Mark, Nov. 2018]
(a) 12.17
(b) 66.69
(c) 39.43
(d) None of these
Solution:
(b)
Given ; Q1 = 54.52 ; Q2 = 78.86.
It is normally distributed i.e. symmetrical data.
∴ Mean = Mode = me = \(\frac{\mathrm{Q}_1+\mathrm{Q}_3}{2}\) = \(\frac{54 \cdot 52+78 \cdot 86}{2}\) = 66.69.
![]()
Question 82.
What is the mean of X having the following density function? [1 Mark, Nov. 2018]
f (x) = \(\frac{1}{4 \sqrt{2 \pi}} e^{\frac{(x-10)^2}{32}}\) for -∞ < x < ∞
(a) 4
(b) 10
(c) 40
(d) None of the above
Solution:
(b)
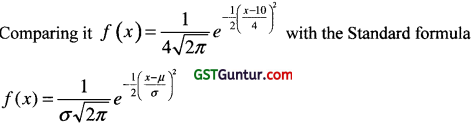
Where -∞ < x < ∞
We get; Mean = μ = 10 and σ = 4
Question 83.
4 coins were tossed 1,600 times. What is the probability that all 4 coins do not turn head upward at a time ? [1 Mark, June 2019]
(a) 1600 e-100
(b) 1000 e-100
(c) 100 e-1600
(d) e-1600
Solution:
(d) Probability of getting a head in a throw of a coin = \(\frac{1}{2}\)
Probability of getting 4 heads upward in a throw of four coins = \(\frac{1}{2^4}\) = \(\frac{1}{16}\) = p(let)
Given that
Here, n = 1600
∴ Mean = m = np
= 1600 × \(\frac{1}{16}\)
= 100
P(No Head)= P (X = 0) = \(\frac{\mathrm{e}^{-100} \cdot(100)^0}{0 !}\) = \(\frac{\mathrm{e}^{-100} \cdot 1}{1}\)
= e-100
![]()
Question 84.
If mean and variance are 5 and 3 respectively then relation between p and q is : [1 Mark, June 2019]
(a) p > q
(b) p < q
(c) p = q
(d) p is symmetric
Solution:
(b)
Mean = 5, ⇒ np = 5; Variance = 3 ⇒ npq = 3
⇒ 5q = 3
⇒ q = 3/5
p = 1 – q = 1 – 3/5 = 2/5
Hence, p < q
Question 85.
In a Poisson distribution if P(x = 4) = P(x = 5) then the parameter of Poisson distribution is : [1 Mark, June 2019]
(a) \(\frac{4}{5}\)
(b) \(\frac{5}{4}\)
(c) 4
(d) 5
Solution:
(d)
Given that in Poisson distribution
P(x = 4) = P (x = 5)

Hence m = 5
![]()
Question 86.
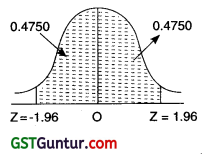
Area between -1.96 to + 1.96 in a normal distribution is : [1 Mark, June 2019]
(a) 95.45%
(b) 95%
(c) 96%
(d) 99%
Solution:
(b)
Area between – 1.96 to + 1.96 in a Normal distribution is 95%.
∵ P(z = 1.96) = 0.4750
∵ P(-1.96 ≤ z ≤ 1.96) = 0.4750 × 2
= 0.9500
= 95%