This Simple Interest – CA Foundation Maths Study Material is designed strictly as per the latest syllabus and exam pattern.
Simple Interest – CA Foundation Maths Study Material
When we borrow money from a bank or co-operative society or an individual institution, for a period of time, we pay some extra money in addition to the money borrowed, to the lender for using his money. This extra money paid is called Interest (I), the amount borrowed is called Principal (P) and the time period for which money is borrowed is called Time (t). The money with interest paid back to the lender is called of Amount (A or S). In other words
Amount = Principal + Interest
A =P + I
Simple Interest
The interest computed on the principal only (i. e. not on interest earned) for the entire period of borrowing is called SIMPLE INTEREST.
Type-I
Some Important Formulae.
(i) I = \(\frac{\text { P.r.t }}{100}\) [when r in %]
(ii) I = p.r.t. [when r in decimal form]
(iii) r = \(\frac{\mathrm{I} \times 100}{\mathrm{pt}}\)
(iv) t = \(\frac{\mathrm{I} \times 100}{\mathrm{pr}}\)
(v) P = \(\frac{\mathrm{I} \times 100}{\mathrm{rt}}\)
(vi) A = P + I
(vii) I = A – P
(viii) A = P\(\left(1+\frac{r t}{100}\right)\)
Where
A = Accumulated amount
[Final value of investment]
P = Principal. [Initial value of an investment]
r = Rate of interest
t = time (years.)
I = Amount if interest
![]()
Illustrative examples:
Example 1
How much interest will be earned on ₹ 2000 at 6% simple interest for 2 years.
Answer:
I = \(\frac{\operatorname{Pr} t}{100}=\frac{2000 \times 6 \times 2}{100}\) = ₹ 240
Example 2
Sarita deposited ₹ 50,000 in a bank for 2 years with the interest rate of 5.5% p.a. what will be the final value of Investment ?
Answer:
A = P(1 + \(\frac{r t}{100}\))
= 50,000[1 + \(\frac{5.5 \times 2}{100}\)] = ₹ 55,500
Calculator Tricks:-
rate for 2 years = 2 × 5.5 = 11% .
Amount = 50000 + 11% button = ₹ 55000
Example 3
F ind the rate of interest if the amount owed after 6 months is ₹ 1050 borrowed amount being ₹ 1000.
(a) 5%
(b) 10%
(c) 15%
(d) None
Answer:
SI = ₹(1050 – 1000) = ₹ 50
r = \(\frac{I \times 100}{p t}=\frac{50 \times 100 \times 12}{1000 \times 6}\) = 10%
Tricks: Go by choices
For (b) A = 1000 + 1000 × rate of interest of 6 months
= 1000 + 1000 × \(\frac{10}{2}\)(%) = ₹ 1050
option (b) is correct
Calculator Tricks:- GBC
For option (b)
r = \(\frac{10}{2}\) = 5%
A = 1000 + 5% button (press) = 1050 (True)
Example 4.
Kapil deposited some amount in a bank for 7\(\frac{1}{2}\) years at the rate of 6% p.a. simple interest. Kapil received ₹ 1,01,500 at the end of the term. Compute initial deposit of Kapil.
(a) ₹ 70,000
(b) ₹ 60,000
(c) ₹ 80,000
(d) None
Answer:
Tricks : Go by Choices
For option (a)
= 70,000 + [6 x 7.5]%
= ₹ 1,01,500 (True)
Option (a) is correct.
![]()
Previous Year Exam Questions
Question 1.
₹ 8,000 becomes ₹ 10,000 in two years at simple interest. The amount that will become ₹ 6,875 in 3 years at the same rate of interest is : [1 Mark, Nov. 2006]
(a) ₹ 4,850
(b) ₹ 5,000
(c) ₹ 5,500
(d) ₹ 5,275
Answer:
Tricks
(b) S.I./year = \(\frac{10000-8000}{2}\) = ₹ 1000
r = \(\frac{1000 \times 100}{8000}\) = 12.5%
P = \(\frac{A m t}{\text { Amt at } ₹ 1}=\frac{6875}{1+0.125 \times 3}\)
= ₹ 5000
∴ (b) is correct.
Question 2.
The rate of simple: interest on a sum of money is 6% p.a. for first 3 years, 8% p.a. for the next five years and 10% p.a. for the period beyond 8 years. If the simple interest accrued by the sum for a period for 10 years is ₹ 1,560. The sum is : [1 Mark, Feb. 2007]
(a) ₹ 1,500
(b) ₹ 12,000
(c) ₹ 3,000
(d) ₹ 5,000
Answer:
(b) is correct.
Single S.I For 1 yrs = (6 × 3 + 8 × 5 + 10 × 2)%
= 78%
Tricks: p = \(\frac{\text { Total } S . I}{S . I \text { on } R s 1}=\frac{1560}{0.78}\) = ₹ 2000
(b) is correct
Question 3.
A sum of money doubles itself in 10 years. The number of years it would treble itself is : [1 Mark, Feb. 2007]
(a) 25 years
(b) 15 years
(c) 20 years
(d) None.
Answer:
(c) is correct.
Tricks : SEE Type XV (ii) of “Quicker BMLRS book”
\(\frac{t_2}{t_1}=\frac{x_2-1}{x_1-1}\)
or \(\frac{t_2}{10}=\frac{3-1}{2-1}\) or t2 = 20 yrs
(c) is correct
Question 4.
A certain sum of money amounts to ₹ 6,300 in two years and ₹ 7,875 in three years nine months at simple interest. Find the rate of interest per annum : [1 Mark, May 2007]
(a) 20%
(b) 18%
(c) 15%
(d) 10%
Answer:
(a) is correct.
Tricks:
S.I = \(\frac{\text { Arsts for } 3.75 \mathrm{yrs}-\text { Amts for } 2 \mathrm{yrs}}{(3.75-2) \mathrm{yrs}}\)
= ₹ 900
P = 6300 – 2 × 900 = ₹ 4500
r = \(\frac{900 \times 100}{4500 \times 1}\) = 20%
![]()
Question 5.
A person borrows ₹ 5,000 for 2 years at 4% p.a. simple interest. He immediately lends to another person at 6\(\frac{1}{4}\)% p.a. for 2 years. Find his gain in the transaction per year: [1 Mark, Nov. 2007]
(a) ₹ 112.50
(b) ₹ 125
(c) ₹ 225
(d) ₹ 167.50
Answer:
(a) % Gain = 6\(\frac{1}{4}\)% – 4 = 2.25%
S.I for 2 yrs. = 5000 × 2.25% × 2 = ₹ 225
S.I per yr. = 5000 × 2.25% = ₹ 112.50
∴ (a) is correct
Question 6.
Two equal sums of money were lent at simple interest at 11 % p.a. for 3 \(\frac{1}{2}\) years and 4\(\frac{1}{2}\) years respectively. If the difference in interests for two periods was ₹ 412.50, then each sum is: [1 Mark, Feb. 2008]
(a) ₹ 3,250
(b) ₹ 3,500
(c) ₹ 3,750
(d) ₹ 4,350
Answer:
(C) Tricks : Difference in interest is due to time
∴ rate of interest for the whole
duration = (11 × 4.5 – 11 × 3.5) = 11%
P = \(\frac{\text { Total S.I }}{\text { Interest on } ₹ 1}=\frac{412.50}{0.11}\) = 3750
(c) is correct
Question 7.
In how much time would the simple interest on a certain sum be 0.125 times the principal at 10% per annum ? [1 Mark, June 2008]
(a) 1\(\frac{1}{4}\) years
(b) 1\(\frac{3}{4}\) years
(c) 2\(\frac{1}{4}\) years
(d) 2\(\frac{3}{4}\) years
Answer:
(a) is correct
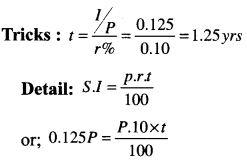
or t = 0.125 × 10 = 1.25yrs
(a) is correct
Question 8.
Find the numbers of years in which a sum doubles itself at the rate of 8% per annum.
(a) 11\(\frac{1}{2}\)
(b) 12\(\frac{1}{2}\)
(c) 9\(\frac{1}{2}\)
(d) 13\(\frac{1}{2}\)
Answer:
(b) is correct
Tricks : t = \(=\frac{(x-1) \times 100}{r}\)
= \(\frac{(2-1) \times 100}{8}\) = 12.5 yrs
![]()
Question 9.
The time by which a sum of money is 8 times of itself if it double itself in 15 years. [1 Mark, June 2009]
(a) 42 years
(b) 43 years
(c) 45 years
(d) 46 years
Answer:
(c) is correct
It is Compound Interest Qts.
Tricks : 2t2 = 815
or 2t2 = (23)15 : t2 =45yrs
Question 10.
What is the rate of simple interest if a sum of money amount ₹ 2,784 in 4 years and ₹ 2,688 in 3 years ? [1 Mark, June 2009]
(a) 1%p.a.
(b) 4%p.a.
(c) 5%p.a.
(d) 8%p.a.
Answer:
(b) is correct

Question 11.
If a simple interest on a sum of money at 6% p.a. for 7 years is equal to twice of simple interest on another sum for 9 years at 5% p.a. The ratio will be: [1 Mark, June 2011]
(a) 2:15
(b) 7:15
(c) 15:7
(d) 1:7
Answer:
(c) is correct

Tricks:- GBC
Question 12.
By mistake a clerk, calculated the simple interest on principal for 5 months at 6.5% p.a. instead of 6 months at 5.5% p.a. If the error in calculation was ₹ 25.40. The original sum of principal was .
(a) ₹ 60,690
(b) ₹ 60,960
(c) ₹ 90,660
(d) ₹ 90,690
Answer:
(b) is correct
P = \(\frac{25.40}{\frac{5.5}{100} \times \frac{6}{12}-\frac{6.5}{100} \times \frac{5}{12}}\)
= \(\frac{25.40 \times 1200}{5.5 \times 6-6.5 \times 5}\) = ₹ 60, 960
Question 13.
It the Simple Interest on ₹ 1,400 for 3 years is less than the simple interest on ₹ 1,800 for the same period by ₹ 80, then the rate of interest is: [1 Mark, Dec. 2011]
(a) 5.67%
(b) 6.67%
(c) 7.20%
(d) 5.00%
Answer:
(b) is correct.
Tricks: r = \(\frac{80 \times 100}{(1800-1400) \times 3}\)
= 6.67%
Question 14.
The S.I. on a sum of money is \(\frac{4}{9}\) of the principal and the No. of years is equal to the rate of interest per annum. Find the rate of interest per annum? [1 Mark, June 2012]
(a) 5%
(b) 20/3%
(c) 22/7%
(d) 6%
Answer:
(b) S.I. = \(\frac{p . r . r}{100} \Rightarrow \frac{4}{9}\)p. = p.\(\left(\frac{r}{10}\right)^2\)
∴ \(\frac{r}{10}=\frac{2}{3}\)
r = \(\frac{20}{3}\)%
Question 15.
Simple interest on ₹ 2,000 for 5 months at 16% p.a. is : [1 Mark, June 2012, Dec. 2012]
(a) ₹ 133.33
(b) ₹ 133.26
(c) ₹ 134.00
(d) ₹ 132.09
Answer:
(a) S.I. = 2000 × \(\frac{5}{12} \times \frac{16}{100}\) = ₹ 133.33
![]()
Question 16.
How much investment is required to yield an Annual income of ₹ 420 at 7% p.a. Simple interest. [1 Mark, Dec. 2012]
(a) ₹ 6,000
(b) ₹ 6,420
(c) ₹ 5,580
(d) ₹ 5,000
Answer:
(a) P = \(\frac{420 \times 100}{7 \times 1}\) = ₹ 6000
Calculator Tricks II GBC :
P = 420 ÷ 7% button = ₹ 6000
Question 17.
Mr. X invests ₹ 90,500 in post office at 7.5% p.a. simple interest. While calculating the rate was wrongly taken as 5.7% p.a. The difference in amounts at maturity is t 9,11 A. Find the period for which the sum was invested. [1 Mark, Dec. 2012]
{a) 7 years
(b) 5.8 years
(c) 6 years
(d) 8 years
Answer:
(c) Tricks
t = \(\frac{9774 \times 100}{90,500 \times(7.5-5.7)}\) = 6yrs
Question 18.
If the sum of money when compounded annually become ₹ 1140 in 2 years and ₹ 1710 in 3 years at rate of interest [1 Mark, June 2013]
(a) 30%
(b) 40%
(c) 50%
(d) 60%
Answer:
(c) Interest in 3rd yr = ₹ 1710 – ₹ 1140
= ₹ 570
Tricks Note : For 3rd yr ; it will be like S.I
r = ∴ \(\frac{I \times 100}{P . t}=\frac{570 \times 100}{1140 \times 1}\) = 50%
Tricks II Go by choices.
For (c) A = 1140 + 50% (Calculator)
= ₹ 1710
(c) is correct
Question 19.
In what time will a sum of money double itself at 6.25% p.a. at simple interest: [1 Mark, Dec. 2013]
(a) 5 yrs
(b) 8 year
(c) 12 yrs
(d) 16yrs
Answer:
(D) Is correct.
Tricks : See Quicker BMLRS.
Question 20.
What principal will amount to ₹ 370 in 6 years at 8% p.a. at simple interest : [1 Mark, Dec. 2013]
(a) ₹ 210
(b) ₹ 250
(c) ₹ 310
(d) ₹ 350
Answer:
(b) is correct
Tricks: P = \(=\frac{370}{1+6 \times 0.08}\) = ₹ 250
(See Quicker BMLRS)
Calculator Tricks GBC
(b) Amt = 250 + (6 x 8)% button press = 370
![]()
Question 21.
If a sum triples in 15 yrs at Simple rate of interest then the rate of interest per annum will be: [1 Mark, June 2014]
(a) 13.0%
(b) 13.3%
(c) 13.5%
(d) 18%
Answer:
(b) is correct
Tricks r = \(\frac{(3-1) \times 100}{1 \times 15}\) = 13.3%
Calculator Tricks GBC
(b) r = 15 × 13.333% = 200%
A = 1 + 200% (button) = 3
(b) is correct
Question 22.
A certain sum of money was invested at simple rate of interest for three years. If it was invested at 7% higher, the interest have been ₹ 882 more, then sum has been invested at that rate was: [1 Mark, Dec. 2014]
(a) ₹ 12,600
(b) ₹ 6,800
(c) ₹ 4,200
(d) ₹ 2,800
Answer:
(c) is correct
S.I = ₹ 882 for r = 7%
t = 3 years.
P = \(\frac{\mathrm{I} \times 100}{r t}=\frac{882 \times 100}{7 \times 3}\) = ₹ 4200
Calculator Tricks: GBC
Question 23.
A sum of money will be doubled itself in 8 years at S.I. In how many years the sum will be tripled itself ? [1 Mark, June 2015]
(a) 20 years
(b) 12 years
(c) 16 years
(d) None
Answer:
(c) is correct.
Tricks: \(\frac{t_2}{8}=\frac{3-1}{2-1}\)
t2 = 16yrs.
Question 24.
A sum of 44,000 is divided into 3 parts such that the corresponding interest earned after 2 years, 3 years and 6 years may be equal at the rate of simple interest are 6% p.a. 8% p.a. & 6% p.a., respectively. Then the smallest part of the sum will be. [1 Mark, June 2015]
(a) ₹ 4,000
(b) ₹ 8,000
(c) ₹ 10,000
(d) ₹ 12,000
Answer:
(b) is correct.

= 6:3:2
So, Smallest principal = \(\frac{44000}{6+3+2}\) × 2 = ₹ 8000
Question 25.
No. of years a sum of money becomes 4 times itself at 12% p.a. at simple interest: [1 Mark, Dec. 2015]
(a) 20
(b) 21
(c) 25
(d) 30
Answer:
(c) is correct
Tricks: t = \(\frac{(4-1) \times 100}{1 \times 12}\) = 25 yrs
Question 26.
If a person lends ₹ 6,000 for 4 years and ₹ 8,000 for 3 years at S.I. The total interest earned is ₹ 2400 then the rate of interest is: [1 Mark, Dec. 2016]
(a) 5%
(b) 6%
(c) 1%
(d) 8%
Answer:
(a) is correct.
Tricks: Go by choices.
For (a);
Total SI = 6000 × 4. × 5% + 8000 × 3 × 5%
= ₹ 2400
So, (a) is correct.
Question 27.
In simple interest, a certain sum becomes ₹ 97,920 in 3 years, and ₹ 1,15,200 in 5 years, then the rate of interest is: [1 Mark, June 2018]
(a) 10%
(b) 11.2%
(c) 12%
(d) 13.6%
Answer:
(c)
Tricks :
S.I p.a = \(\frac{1,15,200-97,920}{5-3}\)
= ₹ 8640
Principal = 97,920 – 3 yrs interest = 97,920 – 3 x 8640 = ₹ 72,000
r = \(\frac{8640 \times 100}{72000}\) = 12%
Calculator Tricks:
Amounts = 72000 + (12 × 3 = 36) % button = ₹ 97,920 (True)
So, option (C) is correct.
![]()
Question 28.
A person borrows Rs. 5,000 for 2 years at 4% per annual simple interest. He immediately lends to another person at 6 – % . Per annual for 2 years find his gain in the transaction . [1 Mark, May 2018]
(a) Rs. 112.50
(b) Rs. 225
(c) Rs. 125
(d) Rs. 107.50
Answer:
(b)
Interest Gain = (6\(\frac{1}{4}\) – 4) = 2\(\frac{1}{4}\) = 2.25%
So, Interest Gain
= \(\frac{5000 \times 2 \times 2.25}{100}\) = Rs. 225
Question 29.
A certain money doubles itself in 10 years when deposited on simple interest. It would triple itself in: [1 Mark, Nov. 2018]
(a) 30 years
(b) 20 years
(c) 25 years
(d) 15 years
Answer:
(b)
Tricks : See Simple Interest (Quicker BMLRS)
\(\frac{t_2}{t_1}=\frac{x_2-1}{x_1-1}\)
⇒ \(\frac{t_2}{10}=\frac{3-1}{2-1}\) ⇒ t2 = 20 yrs.
Question 30.
A certain sum of money Q was deposited for 5 year and 4 months at 4.5% simple interest and amounted to ₹ 248, then the value of Q is: [1 Mark, Nov. 2018]
(a) ₹ 240
(b) ₹ 200
(c) ₹ 220
(d) ₹ 210
Answer:
(b)
t = 5 yrs 4 months = 5 + \(\frac{4}{12}=\frac{16}{3}\) yrs
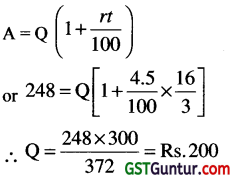
Tricks : GBC
Rates for 5 yrs 4 Months = 5 × 4.5 %+ one third of 4.5% = 24%
Note : 4 months means one third of one year, so rate for 4 months = one third of one year interest rate.
(b) Amounts = 200 + 24% = 248 (True)
So, (b) is correct.
Question 31.
The certain sum of money became Rs. 692 in 2 yrs. and Rs. 800 in 5 yrs. then the principle amount is: [1 Mark, June 2019]
(a) Rs. 520
(b) Rs. 620
(c) Rs. 720
(d) Rs. 820
Answer:
(b)
Tricks:- If a certain sum of money becomes A1 in t1 years and A2 in t2 years then S.I. per annum = \(\frac{A_2-A_1}{t_2-t_1}\)
S.I. p.a = \(\frac{800-692}{5-2}\) = Rs. 36.
Principal = A – Interest
= 692 – Interest of 2 yrs.
= 692 – 2 × 36 = Rs. 620.
(b) is correct.
Question 32.
A sum of money amount to Rs. 6,200 in 2 years and Rs. 7,400 in 3 years as per S.I. then the principal is: [1 Mark, June 2019]
(a) Rs. 3,000
(b) Rs. 3,500
(c) Rs. 3,800
(d) None
Answer:
(c)
Tricks:- S.I. p.a = \(\frac{7400-6200}{3-2}\)
= Rs. 1200.
Principal = 6200 – 2 × 1200
= Rs. 3800.
Question 33.
P = Rs. 5,000; R = 15%; T = 4\(\frac{1}{2}\) using I = \(\frac{\text { PTR }}{100}\) then I will be I = \(\frac{\text { Prt }}{100}\) [1 Mark, June 2019]
(a) Rs. 3,375
(b) Rs. 3,300
(c) Rs. 3,735
(d) None
Answer:
(a)
I = \(\frac{5000 \times 15 \times 4.5}{100}\) = 3375
[Use Calculator ; Never Write]
![]()
Question 34.
In simple interest if the principal is Rs. 2,000 and the rate and time are the roots of the equation x2 – 11x – 30 = 0 then simple interest is : [1 Mark, June 2019]
(a) Rs. 500
(b) Rs. 600
(c) Rs. 700
(d) Rs. 800
Answer:
(b)
∵ x2 – 11x + 30 = 0
or x2 – 5x – 6x + 30 = 0
or x(x – 5) – 6(x – 5)= 0
or (x – 5) (x – 6) = 0
∴ x = 5 ; 6
If r = 5% then t = 6 yrs.
S.I = \(\frac{\operatorname{Pr} t}{100}=\frac{2000 \times 5 \times 6}{100}\)
= Rs. 600.
(b) is correct.