Sequence and Series – Arithmetic & Geometric Progression – CA Foundation Maths Study Material

This Sequence and Series – Arithmetic & Geometric Progression – CA Foundation Maths Study Material is designed strictly as per the latest syllabus and exam pattern.

Sequence and Series – Arithmetic & Geometric Progression – CA Foundation Maths Study Material

Previous Year Exam Questions

Question 1.
The sum of all natural numbers between 100 and 1000 which are multiple of 5 is :
(a) 98,450
(b) 96,450
(c) 97,450
(d) 95,450
Answer:
(a) is Correct
Series is
S = 105 + 110+ 115 + ………………. + 995.
No. of terms = n = \(\frac{l-a}{d}\) + 1 = \(\frac{995-105}{5}\) + 1 = 179
Sum = \(\frac{n}{2}\)(a + l) = \(\frac{179}{2}\) (105 + 995)
= 98,450

Question 2.
Find n such that \(\) may be the geometric mean between a and b:
(a) 1/2
(b) 1
(c) -1/2
(d) 0
Answer:
(c) is correct
Tricks “n + 1 ” must be equal to \(\frac{1}{2}\) (Always)
n + 1 = 1/2 ∴ n = \(\frac{1}{2}\) – 1 = –\(\frac{1}{2}\)

Question 3.
The first and the last terms of an A.P. are – 4 and 146. The sum of the terms is 7171. The number of terms is : [1 Mark, Nov. 2006]
(a) 101
(b) 100
(c) 99
(d) None
Answer:
(a) is correct Given That; a = – 4 ; 1 = 146
Let No. of terms = n.
∴ \(\frac{n}{2}\)(a + l) = 717
or \(\frac{n}{2}\)(-4 + 146) = 7171
or n = \(\frac{7171 \times 2}{142}\) = 101

Question 4.
If the first term of a G.P exceeds the second term by 2 and the sum to infinity is 50, the series is : [1 Mark, Nov. 2006]
(a) 10, 8, \(\frac{32}{5}\), ………
(b) 10, 8, \(\frac{5}{2}\), ……….
(c) 10, \(\frac{10}{3}, \frac{10}{9}\), ……..
(d) None
Answer:
(a) is correct
Tricks Go by choices
a = 10 ; c. r. = r = \(\frac{8}{10}\) = 0..8
S_∞ = \(\frac{a}{1-r}=\frac{10}{1-0.8}\) = 50
∴ (a) is correct.

Question 5.
The sum of square of first n natural numbers is : [1 Mark, Feb. 2007]
(a) \(\frac{n(n+1)}{2}\)
(b) \(\frac{n(n+1)(2 n+1)}{6}\)
(c) \(\frac{n(n-1)(n-1)}{6}\)
(d) \(\frac{n(n+1)(n+2)}{6}\)
Answer:
(b)
1² + 2² + 3² +……………. + to n terms = \(\frac{\mathrm{n}(\mathrm{n}+1)(2 \mathrm{n}+1)}{6}\)

Question 6.
Divide 30 into five parts in A.P., such that the first and last parts are in the ratio 2:3 :
(a) \(\frac{24}{5}, \frac{27}{5}, 6, \frac{33}{5}, \frac{36}{5}\)
(b) 6, \(\frac{36}{5}, \frac{33}{5}, \frac{24}{5}, \frac{27}{5}\)
(c) \(\frac{27}{5}, \frac{24}{4}, \frac{36}{5}, \frac{33}{5}\), 6
(d) 6, \(\frac{24}{5}, \frac{27}{5}, \frac{33}{5}, \frac{36}{5}\)
Answer:
(a) Tricks Go by choices

Question 7.
If a^1/x = b^1/y = c^1/z and a, b, c are in G.P; the x, y, z are in : [1 Mark, Feb. 2007]
(a) A.P.
(b) G.P.
(c) Both (a) & (b)
(d) None
Answer:
(a)
a^1/x = b^1/y = c^1/z = k(let)
∴ a = k^x; b = k^y and c = k^z
∴ a, b, c are in GP
∴ b² = ac
or k^2y = k^xk^z
or k^2y = k^x+y ⇒ 2y = x + z
So x ; y ; z are AP

Question 8.
Find the sum to n terms of the series: [1 Mark, Feb. 2007]
7 + 77 + 777 + …………….. to n terms:

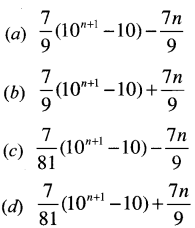
Answer:
(c) is correct
Tricks Go by choices
(c) It n = 2 Then S = 7 + 77 = 84
and \(\frac{7}{81}\)[10²⁺¹ – 10]\(\frac{-7 \times 2}{9}\) = 84
(c) is correct

Question 9.
Find the sum of all natural numbers between 250 and 1,000 which are exactly divisible by 3 : [1 Mark, May 2007]
(a) 1,56,375
(b) 1,56,357
(c) 1,65,375
(d) 1,65,357
Answer:
(a) is correct
S = 252 + 255 + 258 + ………… + 999
n = \(\frac{999-252}{3}\) + 1 = 250 [∵ n = \(\frac{l-a}{d}\) + 1]
s = \(\frac{n}{2}\) (a +1) = \(\frac{250}{2}\)[252 + 999] = 156,375
(a) is correct

Question 10.
If the pth term of a G.P. is x and the qth term is y, then find the nth term:
(a) \(\left[\frac{x^{(n-q)}}{y^{(n-p)}}\right]\)
(b) \(\left[\frac{x^{(n-q)}}{y^{(n-p)}}\right]^{(p-q)}\)
(c) 1
(d) \(\left[\frac{x^{(n-q)}}{y^{(n-p)}}\right]^{\frac{1}{p-q}}\)
Answer:
(d) is correct
Let t, = a and c.r = rof a GP
t_p = a.r^p-1 = x (given) ………… (1)
t_q = a.r^q-1 = y (given) ……….(2)
(1); (2) we get

(d) is correct Tricks!- GBC.

Question 11.
Aperson pays ₹ 975 in monthly instalments, each instalment is less than former by ₹ 5. The amount of first instalment is ₹ 100. In what time will the entire amount be paid? [1 Mark, May 2007]
(a) 26 months
(b) 15 months
(c) Both (a) & (b)
(d) 18 months
Answer:
(b) is correct
Tricks series is
Sn = 100 + 95 + 90 + to n months
Then \(\frac{n}{2}\)[2 × 100 + (n – 1).(-5)] = 975.
Then Go by choices
We get S₂₆ = \(\frac{26}{2}\) [200 +(26 – 1)(-5)] = ₹ 975
and also S₁₅ = \(\frac{15}{2}\) [200 + (15 – 1)(-5)] = ₹ 975
From Quest n = 15 Months will be taken not
= n = 26 because if loan is cleared in 15 months then why should we pay more instalment.
(b) is correct

Question 12.
If the sum of n terms of an A.P. is (3n2 -n) and its common difference is 6, then its first term is: [1 Mark, Aug. 2007]
(a) 3
(b) 2
(c) 4
(d) 1
Answer:
(b) is correct
Tricks S_n =3n² – n (given)
∴ S₁ = t₁
∴ t₁ = s₁ =3x 1² – 1 = 2

Question 13.
Find the sum of the series: 2 + 7 + 12 + ………….. 297. [1 Mark, Aug. 2007]
(a) 8970
(b) 8870
(c) 7630
(d) 9875
Answer:
(a) is correct
S = 2 + 7 + 12 + …………. + 297
n = \(\frac{l-a}{d}=\frac{297-2}{5}\) + 1 = 60
S= \(\frac{n(1+l)}{2}=\frac{60}{2}\) (2 + 297) = 8970
∴ (a) is correct

Question 14.
A certain ball when dropped to the ground rebounds to of the height from which it falls; it is dropped from a height of 100 metres find the total distance it travels before finally coming to rest: [1 Mark, Aug. 2007]
(a) 600m
(b) 700m
(c) 900m
(d) 200m
Answer:
(c) is correct

(c) is correct.

Question 15.
In a G.P if the (p + q)th term is m and (p – q)th term is n, then the pth term is: [1 Mark, Aug. 2007]
(a) mn
(b) \(\sqrt{mn}\)
(c) m²
(d) n²
Answer:
(b) is correct
Let t, = a and c.r = r of GP
t_p+q = a.r^p+q-1 =m
t_p-q =a.r^p-q-1 =n
(1) x (2); we get
a².r^p+q-1+p-q-1 = mn or a²r^2p-2 = mn
or (ar^p-1)1 =mn or ar^p-1 =4mn
t_p = \(\sqrt{mn}\)

Question 16.
The sum of the series: 0.5 + 0.55 + 0.555 + ……….. to n terms is:

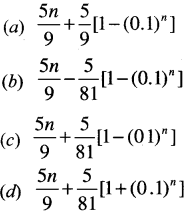
Answer:
(b)
Tricks: Go by choices
Put directly n = 2 That should be equal to
0.5+ 0.55 = 1.05
For (b) \(\frac{5 \times 2}{9}-\frac{5}{18}\) [1 – (0.1)²] = 1.05
(b) is correct

Question 17.
A contractor who fails to complete a building in a certain specified time is compelled to forfeit ₹ 200 for the first day of extra time required and thereafter forfeited amount is increased by ₹ 25 for every day. If he loses ₹ 9,450, for how many days did he over-run the contract time ? [1 Mark, Nov. 2007]
(a) 19 days
(b) 21 days
(c) 23 days
(d) 25 days
Answer:
(b) Tricks:- Series is
S = 200 + 225 + 250 + ……. to n days
= ₹ 9450
\(\frac{n}{2}\) [2 × 200 + (n – 1) × 25] = 9450
Go by choices ; we get
(b) For n = 21
S = \(\frac{21}{2}\)[400 + (21 – 1) × 25] = ₹ 9450
(b) is correct

Question 18.
The first, second and seventh term of an AP. are in G.P. and the common difference is 2, the 2nd term of A.P. is :
(a) 5/2
(b) 2
(c) 3/2
(d) 1/2
Answer:
(a) is correct
Let t₁ = a and c.d = d = 2(given)
t₂ = a + 2; t₁ = a + (7 – 1) × 2 = a + 12
From Question
a ; a+2 ; a + 12 are in GP
or (a + 2)² = a(a + 12)
or a² + 4a + 4 = a² + 12a.
or 12a – 4a = 4
or 8a = 4
a = 4/8 = 1/2
∴ t₂ = a + 2 = \(\frac{1}{2}\) + 2 = \(\frac{5}{2}\)

Question 19.
A man employed in a company is promised a salary of ₹ 3,000 every month for the first year and an increment of ₹ 1,000 in his monthly salary every succeeding year. How much does the man earn from the company in 20 years? [1 Mark, Feb. 2008]
(a) ₹ 30,00,000
(b) ₹ 27,50,000
(c) ₹ 19,10,000
(d) ₹ 7,90,000
Answer:
(a); Series is
S = 3000 × 12 + 4000 × 12 + 5000 × 12 + ……………… to 20 yrs
= 12000 [3 + 4 + 5 + ………….. to 20 terms in AP]
= 12000 × \(\frac{20}{2}\)[2 × 3 + (20 – 1) × 1]
= ₹ 30,00,000
(a) is correct.

Question 20.
If a, b, c are in A.P. and x, y, z are in G.P., then the value of X^(b-c). y^(c-a). z^(a-b) is: [1 Mark, Feb. 2008]
(a) 1
(b) 0
(c) b(c – a)
(d) None
Answer:
(a) is correct
Tricks: a, b, c are in AP
Let a = 1,b = 2 & c = 3 in AP
x, y, z are GP.
Let x = 1 ; y = 2 and z = 4 are in GP
x^(b-c). y^(c-a). z^(a-b)
= 1^2-3. 2^3-1. 4^1-2
= 1.2².4^-1 = 4 × \(\frac{1}{4}\) = 1
(a) is correct

Question 21.
Insert 4 A.M.’s between 3 and 18 : [1 Mark, June 2008]
(a) 12, 15, 9, 6
(b) 6, 9, 12, 15
(c) 9, 6, 12, 15
(d) 15, 12, 9, 6
Answer:
(b)
Only 6, 9, 12, 15 are in AP and 3, 6, 9, 12, 15, 18 makes an AP
(b) is correct

Question 22.
If x’ = 1 + \(\frac{1}{3}+\frac{1}{3^2}\) + ………….. ∞
y = 1 + \(\frac{1}{4}+\frac{1}{4^2}\) + ……. ∞. [1 Mark, June 2008]
Find xy.
(a) 2
(b) 1
(c) 8/9
(d) 1/2
Answer:
(a)

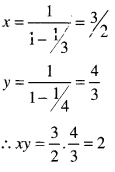
(a) is correct

Question 23.
On 1 st January every year a person buys National Saving Certificates of value exceeding that of his last year’s purchase by ₹ 100. After 10 years, he finds that the total value of the certificates purchased by him is ₹ 54,500. Find the value of certificates purchased by him in the first year :
(a) ₹ 6,000
(b) ₹ 4,000
(c) ₹ 5,000
(d) ₹ 5,500
Answer:
(c) Let 1st yr amount = a and common difference = d = ₹ 100
No. of yrs = n = 10
\(\frac{10}{2}\) [2a + (10 -1) x 100] = 54,500
or 5 [2a + 900] = 54,500
or 2a + 900= 10,900
or 2a= 10900 – 900 = ₹ 1000
a = ₹ 5000
(c) is correct

Question 24.
Find three numbers in G.P. such that their sum is 21, and the sum of their squares is 189 : [1 Mark, June 2008]
(a) 5, 7, 9
(b) 3, 7, 11
(c) 3, 6, 12
(d) 4, 8, 9
Answer:
(c) Tricks Go by choices
(c) Only 3,6, 12 in the given options are in GP
Their sum = 3 + 6+12 = 21 and sum of their squares
3² + 6² + 12² = 189
Satisfy the given conditions
(c) is correct

Question 25.
Find the ninth term of the series : [1 Mark, Dec. 2008]
√2, 5√2, 9√2,
(a) 25√2
(b) 3√2
(c) 33√2
(d) 52√2
Answer:
(c) Given sequence in AP
t₁ = a = √2; and c.d = d = 4√2
t₉ = a + (9 – 1)d = √2 + 8 x 4√2
= 33√2
(c) is correct

Question 26.
The sum of how many terms of the sequence 256, 128, 64, ………………. is 511. [1 Mark, Dec. 2008]
(a) 8
(b) 9
(c) 7
(d) None of these
Answer:
(b) Tricks S = 256 + 128 + 64 + ………………… 10 terms is in GP = 511

Question 27.
(x + 1), 3x, (4x + 2) are in A.P. Find the value of x. [1 Mark, Dec. 2008]
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(b)
x + 1 ; 3x ; 4x + 2 are in AP
3x × 2 = x + 1 + 4x + 2
or 6x = 5x + 3
x = 3
(b) is correct
Tricks:- GBC

Question 28.
Find two numbers whose A.M is 10 and G.M. is 8. [1 Mark, Dec. 2008]
(a) [10, 10]
(b) [16, 4]
(c) [18, 2]
(d) [14, 6]
Answer:
Tricks Go by choices
For (b) A.M = \(\frac{16+4}{2}\) = 10
and GM = \(\sqrt{16 \times 4}\) = 8
(b) satisfies all given conditions
(b) is correct

Question 29.
Σn² defines:
(a) \(\frac{n(n+1)(2 n+1)}{6}\)
(b) \(\frac{n(n+1)}{2}\)
(c) \(\left[\frac{n(n+1)}{2}\right]^2\)
(d) None of these
Answer:
(a) Σn² = 1² + 2² + 3² + ……………………
= \(\frac{n(n+1)(2 n+1)}{6}\) [It is Formula]
(a) is correct.

Question 30.
The sum of terms of an infinite GP is 15. And the sum of the squares of the term is 45. Find the common ratio.
(a) 312
(b) 1
(c) -2/3
(d) 2/3
Answer:
(d) Let t₁ = a and cr. = r
s = a + ar + ar² + …………. to ∞ = 15
∴\(\frac{a}{1-a}\) = 15 ∴ a = 15(1 – r)
and a² + a²r² + a²rA + ………. to ∞ = 45
or a² =45(1 – r²)
or {15(1 – r)}² =45(1 – r)(1 + r)
or 225(1 – r)² = 45 (1 – r)(1 + r)
or 5(1 – r) = 1 + r
or 5 – 5r = 1 + r
or 6r = 4 :-r = 2/3
(d) is correct

Question 31.
If in an A.P., tn represents nth term. If t₇ : t₁₀ = 5 : 1 then t₈ : t_n = [1 Mark, June 2009]
(a) 13: 16
(b) 17: 23
(c) 14: 17
(d) 15: 19
Answer:
(b) Let x is common in the ratio

t1 = 5x and tlQ = 7x
a + 6d = 5x and a + 9d = 7x
Where a 1st term and d = common difference
a + 9d – (a + 6d) = 7x – 5x
or 3d = 2x
∴ d = \(\frac{2}{3}\)x

= 17:23
(b) is correct

Question 32.
The sum of an A P, whose first term is -4 and last term is 146 is 7171 .Find the value of n. [1 Mark, June 2009]
(a) 99
(b) 100
(c) 101
(d) 102
Answer:
(c) \(\frac{n}{2}\) (a + l)
\(\frac{n}{2}\)(-4 + 146) = 7171
\(\frac{n}{2}\)(142) = 7171
or 71n = 7171 = n = 101
(c) is correct

Question 33.
Find the sum to infinity of the following series: 1 – 1 + 1 – 1 + 1 – 1 + ……………………. ∞. [1 Mark, Dec. 2009]
(a) 1
(b) ∞
(c) 1/2
(d) Does not exist
Answer:
(c) S = 1 – 1 + 1 – 1 + 1 – 1 + ……………………. ∞ (GP)
= \(\frac{1}{1-(-1)}=\frac{1}{1+1}=\frac{1}{2}\)
(c) is correct

Question 34.
If a₁, a₂, a₃ represent first, second and third term of an A.P respectively, the first term is 2 and (a₁ + a₂)a₃ is minimum,then the common difference is equal to: [1 Mark, June 2010]
(a) 5/2
(b) -5/2
(c) 2/5
(d) -2/5
Answer:
(b) Given a, = 2
Let c.d = x
∴ a₂ = 2 + x and a₃ = 2 + 2x
The Function is (a₁ + a₂)a₃
= (2 + 2 + x) (2 + 2x)
= (4 + x) (2 + 2x)
= 8 + 8x + 2x + 2x²
= 2x² + 10x + 8 (a Quadratic Function)
Formula;
ax² + bx + c is minimum when
a > 0 i.e. + ve at x = -b/2a
= \(\frac{-10}{2 \times 2}=\frac{-5}{2}\)
(b) is correct

Question 35.
Divide 144 into three parts which are in AP. and such that the largest is twice the smallest, the smallest of three numbers will be : [1 Mark, June 2010]
(a) 48
(b) 36
(c) 13
(d) 32
Answer:
(d) Let t₁ = a and cd = d
a + a + d + a + 2d = 144
or 3a + 3d = 144
or 3(a + d) = 144
a + d = \(\frac{144}{3}\) = 48
a + d = 48
Largest = 2 × Smallest
a + 2d = 2a
2d = a
d = a/2
From (1)
a + \(\frac{a}{2}\) = 48
or \(\frac{3}{2}\)a = 48
a = 48 × \(\frac{2}{3}\)
a = 32
(d) is correct
Tricks: GBC

Question 36.
Sum of series 1 + \(\frac{4}{5}+\frac{7}{5^2}+\frac{10}{5^3}\) + ………… ∞. [1 Mark, June 2010]
(a) 15/36
(b) 35/36
(c) 35/16
(d) 15/16
Answer:

Question 37.
If G be geometric mean between a & b, then the value of \(\frac{1}{G^2-a^2}+\frac{1}{G^2-b^2}\) is equal to: [1 Mark, Dec. 2010]
(a) G
(b) 3G²
(c) 1/G²
(d) 2/G²
Answer:
(c) Tricks: 1, 2, 4 are in GP
∴ 2 is the GM of 1 & 4
∴ a = 1; b = 4 and G = 2

Question 38.
If the sum of n terms of an A.P. is 2n² + n. What is the difference between its 10th term & 1st term: [1 Mark, June 2011]
(a) 207
(b) 36
(c) 90
(d) 63
Answer:
(b) S_n = 2n² + n
∴ t₁ = s₁ = 2 × 1² + 1 = 3
s₂ = 2 2² + 2 = 10
∴ d = s₂ – 2s₁ = 10 – 2 × 3 = 4
∴ t₁₀ – t₁ = a + 9d – a= 9d = 9 × 4
= 36
∴ (b) is correct

Question 39.
Find the product of 243.243².243^{\(\frac{1}{6}\)}.243^{\(\frac{1}{36}\)}………. to ∞
(a) 1024
(b) 27
(c) 729
(d) 246
Answer:
(c) is correct
P = (243).(243)^{\(\frac{1}{6}\)}.(243)^{\(\frac{1}{36}\)}………. to ∞
= 243\(\frac{1}{1-1 / 6}\) = 243^6/5 = (3⁵)^6/5
= 3⁶ = 729

Question 40.
Insert two arithmetic means between 68 and 260. [1 Mark, June 2011]
(a) 132, 196
(b) 130, 194
(c) 70, 258
(d) None
Answer:
(a) Trick I
A₁ + A₂ + A₃ + ………….. + A_n = n × AM of a&b
= n\(\)
132 + 196 = 2\(\left(\frac{68+260}{2}\right)\)
328 = 328 (True)
Trick II
Go by choices
For (a) 68, 132, 196, 260 marks an AP
(a) is correct

Question 41.
Geometric mean of p, p², p³ ………. pⁿ will be
(a) pⁿ⁺¹
(b) p^{\(\left(\frac{1+n}{2}\right)\)}
(c) p\(\frac{n(n+1)}{2}\)
(d) None of the above
Answer:
(b)
GM = (p.p² .p³ …………. pⁿ)^1/n
= (p^{1+2+3+………..+n})^1/n
= [p^{\(\frac{n(n+1)}{2}\)}] = p^(n+1/2)

Tricks Put n = 3
GM = (p.p².p³)^1/3 = p²
For (a) GM = p³⁺¹ ≠ p²
(b) GM = p^{\(\frac{1+3}{2}\)} = p²
(b) is correct.

Question 42.
Find the number whose arithmetic mean is 12.5 and geometric mean is 10. [1 Mark, Dec. 2011]
(a) 20 and 5
(b) 10 and 5
(c) 5 and 4
(d) None of these
Answer:
(a) is correct
Tricks Go by choices
For (a) AM = \(\frac{20+5}{2}\) = 12.5
and GM = \(\sqrt{20 \times 5}\) = 10
20 & 5 satisfy both given condition in qts.
(a) is correct.

Question 43.
If sum 3 arithmetic mean between “a” and 22 is 42, then “a”= _______. [1 Mark, Dec. 2011]
(a) 14
(b) 11
(c) 10
(d) 6
Answer:
(d) is correct
Tricks It A₁; A₂; A₃; …………; A_n are “n” AMS between a and b
A₁ + A₂ + A₃ + ……………. + A_n
= n.(AM of a and b)
∴ 3\(\left(\frac{a+22}{2}\right)\) = 42
∴ a = 6

Question 44.
If each month ₹ 100 increases in any sum then find out the total sum after 10 months, if the sum of first month is ₹ 2,000. [1 Mark, Dec. 2011]
(a) ₹ 24,500
(b) ₹ 24,000
(c) ₹ 50,000
(d) ₹ 60,000
Answer:
(a) Sum = \(\frac{10}{2}\)[2 × 2000 + (10 – 1).100]
= ₹ 24,500.

Question 45.
If 5th term of a G.P. is \(\sqrt[3]{3}\), then the product of first nine terms is: [1 Mark, Dec. 2011]
(a) 8
(b) 27
(c) 243
(d) 9
Answer:
(b);
t₅ = a.r4 = \(\sqrt[3]{3}\) = 31/3
Product of 1 st 9 terms
= a. ar, ar² …………… ar⁸
= a⁹.r^{1+2+3+……….+8}
= (ar⁴)⁹ = (3>3)⁹ = 3³ = 27

Question 46.
The sum of the third and ninth term of an A.P. is 8. Find the sum of the first 11 terms of the progression. [1 Mark, Dec. 2011]
(a) 44
(b) 22
(c) 19
(d) 11
Answer:
(a) is correct
∵ t₃ + t₉ = 8
a + 2d + a + 8d
or 2a + 10d = 8
∴ S₁₁ = \(\frac{11}{2}\)[2a + (11 – 1)d]
= \(\frac{11}{2}\) [2a + 10d] = \(\frac{11}{2}\) × 8 = 44

Question 47.
8th term of an A.P is 15, then sum of its 15 terms is: [1 Mark, June 2012]
(a) 15
(b) 0
(c) 225
(d) 225/2
Answer:
(c) is correct to
t₈ = a + 7d = 15
S₁₅ = \(\frac{15}{2}\)[2a + (15-1)d] = \(\frac{15}{2}\) × 2(a + 7d)
= 15 × 15 = 225

Question 48.
Find the sum of the infinite terms
2, \(\frac{4}{y}, \frac{8}{y^2}, \frac{16}{y^3}\), …………. If y > 2. [1 Mark, June 2012]
(a) \(\frac{2 y}{y-2}\)
(b) \(\frac{4 y}{y-2}\)
(c) \(\frac{3 y}{y-2}\)
(d) None of these
Answer:
(a) is correct
s = \(\frac{a}{1-r}=\frac{2}{1-\frac{2}{y}}=\frac{2 y}{y-2}\)

Question 49.
The 4th term of an A.P. is three times the first and the 7th term exceeds twice the third term by 1. Find the first term ‘a’ and common difference ‘d’. [1 Mark, June 2012]
(a) a = 3, d = 2
(b) a = 4, d = 3
(c) a = 5, d = 4
(d) a = 6, d = 5
Answer:
(a) is correct
t₄ = 3t ⇒ a + 3d = 3a
2a = 3d; a = \(\frac{3 \mathrm{~d}}{2}\)
∵ t₇ = 2t₃ + 1
or a + 6d = 2(a + 2d) +1
or a + 6d = 2a + 4d + 1
or 2d – a = 1
or 2d – \(\frac{3}{2}\) d = 1 ⇒ \(\frac{d}{2}\) = 1
d = 2
and a = \(\frac{3}{2}\) × 2 = 3
Tricks: Go by choices.

Question 50.
In an A.P., if common difference is 2, Sum of n terms is 49,7th term is 13 then n = ______. [1 Mark, Dec. 2012]
(a) 0
(b) 5
(c) 7
(d) 13
Answer:
(c) is correct.
t₇ = a + 6 × 2 = 13 ∴ a = 1
s_n = \(\frac{n}{2}\)[2 × 1 + (n – 1).2] = 49
or \(\frac{n}{2}\) .2[1 + n – 1] = 49
or n² = 49 ∴ n = 7

Question 51.
The first term of a G.P. where second term is 2 and sum of infinite term is 8 will be: [1 Mark, Dec. 2012]
(a) 6
(b) 3
(c) 4
(d) 1
Answer:
(c) is correct
t₂ = ar = 2 ⇒ r = \(\frac{2}{a}\)
S_∞ = \(\frac{a}{1-r}\) = 8
or a = 8 (1 – r)
or a² = 8(a – 2)
or a² – 8a + 16 = 0
or (a – 4)² = 0 ⇒ a = 4
Tricks Go by choices
For (c) 4r = 2 ∴ r = \(\frac{1}{2}\)
S = \(\frac{9}{1-r}=\frac{4}{1-1 / 2}\) = 8 (Which is correct)
(c) is correct

Question 52.
If the sum of n terms of an A.P be 2n² + 5 n, then its ‘nth’ term is: [1 Mark, Dec. 2012]
(a) 4n – 2
(b) 3n – 4
(c) 4n + 3
(d) 3n + 4
Answer:
(c) is correct
S₁ = 2n² + 5n
S₁ = t₁ = 2 × 1² + 5 × 1 = 7 = a
d = S₂ – 2S₁
= 2 × 2² + 5 × 2 – 2 × 7 = 4
t_n = a + (n – 1)d = 7 + (n -1)4 = 4n + 3
Tricks Go by choices
For (a) S₁ = t₁ = 4 × 1 – 2 = 2 ≠ 7
(c) t₁ = 4 × 1 + 3 = 7
t₂ =4 × 2 + 3 = 11
S₂ = t₁ + t₂ = 7 + 11 = 18
and S₂ = 2 × 22 + 5 × 2 = 18
(c) Satisfies it (c) is correct.

Question 53.
In an A.P. if s_n = 3n² – n and its common difference is 6 then first term is: [1 Mark, June 2013]
(a) 2
(b) 3
(c) 4
(d) 6
Answer:
(a) is correct.
s_n = 3 n² – n
s₁ = 3 × 1² – 1 = 2 = t₁
1 st term = 2

Question 54.
In an A.P if the sum of 4th & 12th term is 8 then sum of first 15 term is: [1 Mark, June 2013]
(a) 60
(b) 120
(c) 110
(d) 150
Answer:
(a) is correct.
Given, t₄ + t_n = 8
or a + 3d + 1 + 11d = 8
or 2a + 14d = 8
∴ S₁₅ = y[2a + (15 – 1)d]
= \(\frac{15}{2}\) × 8 = 60
(a) is correct

Question 55.
There are ‘n’ AMs between 7 & 71 and 5th AM is 27 then ‘n’ = [1 Mark, June 2013]
(a) 15
(b) 16
(c) 17
(d) 18
Answer:
(a) is correct.
c.d = \(\frac{b-a}{n+1}\) (Tricks)
= \(\frac{71-7}{n+1}=\frac{64}{n+1}\)
As = a + 5d (Tricks)
= 7 + 5 x \(\frac{64}{n+1}\) = 27
or \(\frac{64}{n+1}\) = 20
or 20n + 20 = 320
or 20n = 300
∴ n =15
∴ (a) is correct

Question 56.
In a G.P the 6th term is 729 and the common ratio is 3 then is: [1 Mark, June 2013]
(a) 2
(b) 3
(c) 4
(d) 7
Answer:
(b) is correct.
t₁ = a; cr = r = 3
t₆ = 729
or a.r⁵ = 729
or a × 3⁵ = 36
a = 3

Question 57.
An AP has 13 terms whose sum is 143.The third term is 5, then first term is: [1 Mark, Dec. 2013]
(a) 4
(b) 7
(c) 9
(d) 2
Answer:
(d) is correct
:.t₃ = a + 2d = 5 ………….(1)
2d = 5 – a
s₁₃ = \(\frac{13}{2}\)[2a + (13 – 1)d] = 143
or 2a+ 12d = \(\frac{143 \times 2}{13}\) = 22 or a + 6d = 11
or a + 3 × 2d = 11
or a + 3 (5 – a) =11
or a + 15 – 3a = 11
or 4 = 2a
∴ a = 2
Tricks Go by choices
[Solve mentally by calculator]

Question 58.
G.M of a, b, c, d is 3 then G.M of — is
(a) \(\frac{1}{3}\)
(b) 3
(c) \(\frac{1}{81}\)
(d) 81
Answer:
(a) is correct
G = 3 = (abcd)^1/4 ……………(1)
New GM = \(\left(\frac{1}{a} \cdot \frac{1}{b} \cdot \frac{1}{c} \cdot \frac{1}{d}\right)^{1 / 4}=\frac{1}{3}\)
Tricks: GM of a, b, c, d = 3
GM of their reciprocals = \(\frac{1}{3}\)

Question 59.
The value of 1³ + 2³ + 3³ + ………… + m³ is equal to: [1 Mark, June 2014]
(a) \(\left[\frac{m(m+1)}{2}\right]^3\)
(b) \(\frac{m(m+1)(2 m+1)}{6}\)
(c) \(\left[\frac{m(m+1)}{2}\right]^2\)
(d) None
Answer:
(c) is correct
Formula = \(\left\{\frac{m(m+1)}{2}\right\}^2\)

Question 60.
The sum of the infinite GP 1 + \(\) + …….. ∞ is equal to: [1 Mark, June 2014]
(a) 1.95
(b) 1.5
(c) 1.75
(d) None
Answer:
(b) is correct
S_∞ = \(\frac{a}{1-r}=\frac{1}{1-\frac{1}{3}}=\frac{3}{2}\) = 1.5

Question 61.
The sum of m terms of the series is 1 + 11 + 111 + ……….. is equal to: [1 Mark, June 2014 June 2015]
(a) \(\frac{1}{81}\)[10^m+1 – 9m – 1o]
(b) \(\frac{1}{2}\)[10^m+1 – 9m – 1o]
(c) [10^m+1 – 9m – 10]
(d) None of these
Answer:
(a) is correct
Tricks Go by choices
For (a) put m = 1 ; we get
5 = \(\frac{1}{81}\)[10¹⁺¹ – 9 × 1 – 10] = 1 = 1st term
Put m = 2; S= \(\frac{1}{81}\)[192 + 1 – 9 × 2 – 10] = 12
= 1 + 11 = Sum of 1st 2 terms
So; (a) is correct.

Question 62.
If the sum of first ‘n’ terms of an A.P is 6n2 + 6n, then the fourth term of the series: [1 Mark, Dec. 2014]
(a) 120
(b) 72
(c) 48
(d) 24
Answer:
(c) is correct
S = Sum of 1 st n terms of as AP.
= 6n² + 6n
a = t₁ = s₁ = 6 × 1² + 6 × 1 = 12
S₂ = 6 × 2² + 6 × 2 = 36
c,d = d = s₂ – 2s₁ = 36 – 2 × 12 = 12
t₄ = a + (4 – 1)d = 12 + 3 × 12 = 48

Question 63.
If S_n = n²p and S_m = m²p ; (m ^ n) is the sum of A.P., then S_p = [1 Mark, Dec. 2014]
(a) p²
(b) p³
(c) 2p³
(d) p⁴
Answer:
(b) is correct
∵ s₂ = n²p
s_m = m²p
∴ s_p = p .p = p

Question 64.
If x, y,z are the terms in G.P then the terms x² + y², xy + yz, y² + z² are in: [1 Mark, Dec. 2014]
(a) A.P
(b) G.P
(c) H.P
(d) None of these
Answer:
(b) is correct
∵ x; y; z are inG.P
Tricks:- Let x = 1; y = 2; z = 4 make a G.P
x² + y² = 1² + 2² = 5
xy + yz = 1 × 2 + 2 × 4 = 10
y² + z² = 2² + 4² = 20
x² + y²; xy + yz; y² + z² =
5, 10, 20 ………… clearly are in G.P.

Question 65.
Let S be the sum, P be the product and R be the sum of reciprocals of n terms of a G.P then P²Rⁿ. [1 Mark, June 2015]
(a) S²ⁿ
(b) S^-n
(c) Sⁿ
(d) S^-2n
Answer:
Let n = 3
Let S = 1+ 2 + 4 ………. a GP. = 7
Tricks:- P = 1 × 2 × 4 = 8
R = \(\frac{1}{1}+\frac{1}{2}+\frac{1}{4}=\frac{4+2+1}{4}=\frac{7}{4}\)

Let n = 3
P²Rⁿ = P²R³ = 8² × \(\left(\frac{7}{4}\right)^3\) = 64 × \(\frac{349}{64}\) = 7
= s³
= sⁿ
∴ (c) is correct.

Question 66.
The sum of n terms of an AP is 3n² + 5n, which last term is 164.
Answer:
(b) is correct
Sn = 3n² + 5n
a = t₁ = S₁ = 3 × 1² + 5 × 1 = 8
S₂ = 3 × 2² + 5 × 2 = 22
d = S₂ – 2S₁
= 22 – 2 × 8 = 6
n = \(\frac{t_n-a}{d}\) + 1 = \(\frac{164-8}{6}\) + 1 = 27

Question 67.
Three No’s a,b,c are in A.P find a – b + c. [1 Mark, Dec. 2015]
(a) a
(b) -b
(c) b
(d) c
Answer:
(c) is correct
let a = 1; b = 2; c = 3 makes an A.P.
∴ a – b + c = 1 – 2 + 3 = 2 = b.

Question 68.
Find the numbers whose GM is 5 and AM is 7.5: [1 Mark, Dec. 2015]
(a) 12 and 13
(b) 13.09 and 1.91
(c) 14 and 11
(d) 17 and 19
Answer:
(b) is correct
Tricks: Go by choices
GM = \(\sqrt{13.09 \times 1.51}\) = 5 (approx)
AM = \(\frac{13.09+1.91}{2}\) = 7.5

Question 69.
If \(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\) are in Arithmetic Progression then a², b², c² are in ______. [1 Mark, June 2016]
(a) Arithmetic Progression
(b) Geometric Progression
(c) Both A.P & GP
(d) None of these
Answer:
(a)
Tricks: a², b², c² are in AP.
a = 1, b = 5, c = 7 Make it in A.P
let

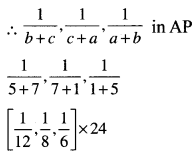
2, 3, 4 is also in A.P
∴ Our Assumption is correct.

Question 70.
The Sum of n terms of the series If log(x) + log\(\left(\frac{x^2}{y}\right)\) + log\(\left(\frac{x^3}{y^2}\right)\) + …….. is: [1 Mark, June 2016]

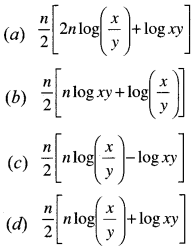
Answer:
(d) is correct.
Tricks: Go by Choices
Put n = 1, 2 Then
(d) Should be equal to first term i.e log x
∴ Option (d)
= \(\frac{1}{2}\)[1.log\(\frac{x}{y}\) + log xy]
= \(\frac{1}{2}\)[log(\(\frac{x}{y}\)xy)]
= \(\frac{1}{2}\)log x²
= \(\frac{1}{2}\)2log x = log x
if n = 2
then option (d) should be equal to log x + log \(\frac{x^2}{y}\) = log\(\frac{x^3}{y}\)
Option (d)

Question 71.
A G.P (Geometric Progression) consists of 2n terms. If the sum of the terms occupying the odd places is S₁ and that of the terms in even places is S₂. The common ratio of the progression is: [1 Mark, June 2016]
(a) n
(b) 2 S₁
(c) \(\frac{\mathrm{S}_2}{\mathrm{~S}_1}\)
(d) \(\frac{\mathrm{S}_1}{\mathrm{~S}_2}\)
Answer:
(c) Tricks
let S = 1 + 2 + 4 + 8 + 16 + ……………. to 2n terms
S₁ = 1 + 4 + 16 + … ton terms
S₂ = 2 + 8 + 32 + … ton terms
for n = 1
S₁ = 1; S₂ = 2
c.r. = \(\frac{S_2}{S_1}=\frac{2}{1}\) = 2 (True)
for n = 2
c.r. = \(\frac{2+8}{1+4}\) = 2 (Also True)
(c) is correct.

Question 72.
2.353535 ……….. = 2.35 [1 Mark, Dec. 2016]
(a) \(\frac{233}{99}\)
(b) \(\frac{234}{99}\)
(c) \(\frac{232}{99}\)
(d) None
Answer:
(a) is correct
tricks: Go by choices [Use calculator]

Question 73.
The number of terms of the series needed for the sum of the series 50 + 45 + 40 + ……….. becomes zero. [1 Mark, Dec. 2016]
(a) 22
(b) 21
(c) 20
(d) None
Answer:
(b) is correct.
Tricks : Go by choices
Let (b) is correct.
S₂₁ = \(\frac{21}{2}\)[2 × 50 + (21 – 1) × (-5)] = 0
So, (b) is correct.

Question 74.
A person received the salary for the 1st year is ₹ 5,00,000 per year and he received an increment of ₹ 15,000 per year then the sum of the salary he taken in 10 years. [1 Mark, Dec. 2016]
(a) ₹ 56,75,000
(b) ₹ 72,75,000
(c) ₹ 63,75,000
(d) None of these
Answer:
(a) is correct.
S₁₀ = \(\frac{10}{2}\)[2 × 5,00,000 + (10 -1) × 15000]
= ₹ 56,75,000.

Question 75.
If a, -3, b, 5, c are in A.P then the value of c is: [1 Mark, June 2017]
(a) -7
(b) 1
(c) 9
(d) 13
Answer:
a, -3 ; b ; 5, are in AP.
So, b = \(\frac{-3+5}{2}\) [b is A.M of -3 & 5]
b = 1
Similarly;
5 = \(\frac{-3+5}{2}\) b + c = 10
or c = 10 – b = 10 – 1 = 9
(c) is correct

Question 76.
The sum of n terms of the series 1 + (1 + 3) + (1 + 3 + 5) +… . [1 Mark, June 2017]
(a) \(\frac{n(n+1)(2 n+1)}{6}\)
(b) \(\frac{n(n+1)(2 n+1)}{3}\)
(c) \(\frac{n(n+1)(n+2)}{6}\)
(d) None
Answer:
Tricks Go by Choices
For (a) put n = 1 ⇒ It should be equal
\(\frac{1(1+1)(2 \times 1+1)}{6}\) = 1 (True)
If n = 2 Then it should be equal to sum of 1st 2 term
So; \(\frac{2(2+1)(2 \times 2+1)}{6}\) = 1 + (1 + 3)
or \(\frac{30}{6}\) = 5 (True)
Option (a) is correct.

Question 77.
The sum of first 20 terms of a G.P is 1025 times the sum of first 10 terms then the common ratio is ______
(a) 2
(b) 2√2
(c) \(\frac{1}{2}\)
(d) √2
Answer:
Given
S₂₀ = 1025. S₁₀
\(\frac{a\left(r^{20}-1\right)}{r-1}\) = 1025. \(\frac{a\left(r^{10}-1\right)}{r-1}\)
or; r²⁰ – 1 = 1025 (r¹⁰ – 1)
or; (r¹⁰)² – 1² = 1025 (r¹⁰ – 1)
or; (r¹⁰ + 1) (r¹⁰ – 1) = 1025 (r¹⁰ – 1)
or ; r¹⁰ + 1 = 1025
or; r = 2
Option (a) is correct.

Question 78.
Find the sum of all natural numbers between 100 and 1000 which are divisible by 11 is : [1 Mark, Dec. 2017]
(a) 44,550
(b) 66,770
(c) 55,440
(d) 33,440
Answer:
(a)
Series
S = 110 + 121 + 132 + ………… + 990
n = \(\frac{l-a}{d}\) + 1 = \(\frac{990-110}{11}\) + 1 = 81
S = \(\frac{n}{2}\)(a + l) = \(\frac{81}{2}\)(110 + 990) = 44,550

Question 79.
If pth, qth, rth terms of a GP. be a, b, c respectively, then (q – r) log a + (r – p) log b + (p – q) log c = [1 Mark, June 2018]
(a) 0
(b) 1
(c) 2
(d) None
Answer:
(a)
Tricks It is in cyclic order.

Question 80.
If a, b, c, d are in GP then (b – c)² + (c – a)² + (d – b)² = ? [1 Mark, June 2018]
(a) (a – b)²
(b) (a – d)²
(c) (c – d)²
(d) 0
Answer:
(b)
a, b, c, d → in GP
let a = 1; b = 2; c = 4; d = 8 in G.P.
∴ (b – c)² + (c – a)² + (d – b)²
= (2 – 4)² + (4 – 1)² + (8 – 2)²
= 4 + 9 + 36 = 49 = 7²
GBC
For (b) (a – d)² = (1 – 8)² = 72 = 49.
(b) is correct.

Question 81.
If the n th term of a series, a_n = 3ⁿ – 2ⁿ then S_n = ? [1 Mark, June 2018]
(a) \(\frac{3}{2}\)(3ⁿ – 1) + 1(n + 1)
(b) \(\frac{3}{2}\)(3ⁿ + 1) – 1(n + 1)
(c) \(\frac{3}{2}\)(3ⁿ – 1) – n(n + 1)
(d) \(\frac{3}{2}\)(3ⁿ + 1) – 1(n – 1)
Answer:
(c)
∵ a_n = 3ⁿ – 2ⁿ
a₁ = 3¹ – 2¹ = 1
a₂ = 3² – 2² = 5
s₂ = a₁ + a₂ = 1 + 5 = 6
Tricks Go by choices (GBC) for (c) let ‘

(c) is correct.

Question 82.
The sum to m terms of the series 1 + 11_111 + …………….. upto m terms, is equal to : [1 Mark, May 2018]
(a) \(\frac{1}{81}\)(10^m+1 – 9m – 10)
(b) \(\frac{1}{27}\)(10^m+1 – 9m – 10)
(c) 10^m+1 – 9m – 10
(d) None of these
Answer:
(a)
Tricks :-GBC
If m = 1 ⇒ S₁ = Sum of 1st 1 term = 1
If m = 2 ⇒ S₂ = Sum of 1st 2 term = 1 + 11 = 12
Note:- Check only for m = 1 and m = 2
(a) If m = 1
S₁ = \(\frac{1}{81}\) (10¹⁺¹ – 9 × 1 – 10)= \(\frac{1}{81}\) (100 – 9 – 10) = 1
(a) If m = 2
S₂ = \(\frac{1}{81}\)[10²⁺¹ – 9 × 2 – 10] = 12
So; Option (a) is true for m = 1 & m = 2.
So; (a) is correct.

Question 83.
A person pays Rs. 975 in monthly instalments, each instalment is less than former by Rs. 5. The amount of 1st instalment is ₹ 100. In what time will be entire amount be paid? [1 Mark, May 2018]
(a) 26 months
(b) 15 months
(c) Both (a) & (b)
(d) 18 months
Answer:
(b)
Tricks:- Go by choices (GBC)
Series
S = 100 + 95 90 + ………… to n months (let)
= 975.
1st check for n = 15 months
S = \(\frac{15}{2}\)[2 × 100 + (15 – 1) – (-5)]
If loan is paid of f in n = 15 months, then no need of other instalments. So (b) is correct.

Question 84.
If the sum of n terms of an AP is (3n2-n) and its common difference is 6, then its first term is : [1 Mark, May 2018]
(a) 3
(b) 2
(c) 4
(d) 1
Answer:
(b)
S_n = 3n² – n
Tricks
∵ t₁ = S₁ = 3 × 1² – 1 = 2 = sum of 1st 1 term.

Question 85.
Insert two arithmetic means between 68 and 260. [1 Mark, May 2018]
(a) 132, 196
(b) 130, 194
(c) 70,258
(d) None
Answer:
(a)
Tricks:
Go by choices
(a) 68; 132; 196; 260 areinAP.
Hence ; 132 ; 196 are A.Ms. b/w 68 and 260.
Hence (a) is correct.

Question 86.
If the pth term of an A.P. is ‘q’ and the qth term is ‘p’, then its rth term is: [1 Mark, Nov. 2018]
(a) p + q + r
(b) p + q – r
(c) p – q – r
(d) p + q
Answer:
(b)
c.d = \(\frac{\mathrm{q}-\mathrm{p}}{\mathrm{p}-\mathrm{q}}=\frac{(\mathrm{p}-\mathrm{q})}{\mathrm{p}-\mathrm{q}}\) = 1
t_r = t_p + (r – p)d
= q + (r – p)(-1)
= q + p – r

Question 87.
The 3rd term of a GP. is \(\frac{2}{3}\) and the 6th term is \(\frac{2}{81}\), then the 1st term is
(a) 2
(b) 6
(d) 9
(d) \(\frac{1}{3}\)
Answer:
(b)

Question 88.
The sum of the series -8, -6, -4,…n terms is 52. The number of terms n is
(a) 10
(b) 11
(c) 13
(d) 12
Answer:(c)
Series S = -8 -6 -4 …………… to n terms
first term = -8 ; c.d = d = 2
Tricks Go by choices (Use calculator)
option (c) S₁₃ = \(\frac{13}{2}\)[2 × (-8) + (13 – 1) × 2] = 52

Question 89.
The value of K, for which the terms 7K + 3, 4K – 5, 2K + 10 are in A.P., is: [1 Mark, Nov. 2018]
(a) -13
(b) -23
(c) 13
(d) 23
Answer:
(b)
Formula 2A = a + b
∴ 2(4k – 5) = 7k + 3 + 2k + 10
or 8k – 10 = 9k + 13
or k = -23

Question 90.
The ratio of sum of n terms of the two AP’s is (n + 1) then the ratio of their m terms is: [1 Mark, June 2019]
(a) (m + 1):2m
(b) (m + 1): (m – 1)
(c) (2m – 1):(m + 1)
(d) m:(m – 1)
Answer:
Given that
\(\frac{S_n^1}{S_n^{11}}=\frac{n+1}{n-1}\)
Tricks
To find the ratio of rth term ; put n = 2r – 1
Put n = 2m – 1
Ratio of mth term
= \(\frac{2 m-1+1}{2 m-1-1}=\frac{2 m}{2 m-2}\)
= \(\frac{2 m}{(2 m-2)}=\frac{m}{m-1}\)
(d) is correct.

Question 91.
In a G.P. if the fourth term is ‘3 ’ then the product of first seven terms is: [1 Mark, June 2019]
(a) 35
(b) 37
(c) 36
(d) 38
Answer:
(b)
Tricks:-
Product of 1st (2r – 1) terms of a G.P = (t_r)^2r-1
∴ t₄= 3
So, Product of 1st 2 × 4 – 1 = 7 terms
= (t_r)^2×4-1 = 3⁷
(b) is correct

Details:
∵ Product of 1st 7 terms
= a.ar.ar².ar³ …………. ar⁶
= a⁷. r^1+2+3+….+6
= a⁷.r^{\(\frac{6}{2}\)(6+1)} = a⁷.r²¹
= a⁷.r²¹
= (ar³)⁷ = 3⁷

Question 92.
If 2 + 6 + 10 + 14 + 18 + …………… + x = 882 then the value of x. [1 Mark, June 2019]
(a) 78
(b) 80
(c) 82
(d) 86
Answer:
(c)
S = 2 + 6+10 + 14 …………….. + x (to n terms)
= 882
∴ \(\frac{n}{2}\)[2 + x] = 882 ……..(1)
where x =Last term
Last term = x = 2 + (n – 1) × 4
x = 4n – 2
or 4n = x + 2
or n = \(\frac{x+2}{4}\)
∴ From (1); we get
\(\frac{(x+2)}{4 \times 2}\)(x + 2) = 882
or (x + 2)² = 8 × 882 = 84²
x + 2 = 84
⇒ x = 82

Tricks:
Let t_n = x
or 2 + (n – 1)4 = x
or 4n – 2 = x
or n = \(\frac{x+2}{4}\)

For GBC
(c) If x = 82 ⇒ n = \(\frac{82+2}{4}\) = 21
∴ S = \(\frac{n}{2}\)(a + l) = \(\frac{21}{2}\)(2 + x)
= \(\frac{21}{2}\)(2 + 82) = 882
∴ (c) is correct

Question 93.
If y = 1 + x + x² + ……… ∞ then x = [1 Mark, June 2019]
(a) \(\frac{y-1}{y}\)
(b) \(\frac{y+1}{y}\)
(c) \(\frac{y}{y+1}\)
(d) \(\frac{y}{y-1}\)
Answer:
(a)
y = 1 + x + x² + ……… ∞ are in G.P
∴ y = \(\frac{1}{1-x}\) Where c.r = x
or 1 – x = \(\frac{1}{y}\)
or x = 1 – \(\frac{1}{y}=\frac{y-1}{y}\)
[S_∞ = \(\frac{a}{1-r}\)]