Students should practice Security Analysis & Portfolio Management – CS Executive Financial and Strategic Management MCQ Questions with Answers based on the latest syllabus.
Security Analysis & Portfolio Management – Financial and Strategic Management MCQ
Question 1.
Security Analysis is a process of estimating individual securities.
(A) Return and risk
(B) Risk and correlation
(C) Correlation and co-efficient
(D) Return and co-efficient
Answer:
(A) Return and risk
Question 2.
Standard deviation determine____
(A) Systematic risk of a security
(B) Unsystematic risk of security
(C) Total risk of security
(D) Premium of security
Answer:
(C) Total risk of security
Question 3.
Financial Assets are –
(A) Pieces of paper representing an indirect claim to real assets in form of debt or equity commit¬ments.
(B) Tangible, material things such as buildings, furniture, automobiles, etc.
(C) Both (A) and (B)
(D) Neither (A) nor (B)
Answer:
(A) Pieces of paper representing an indirect claim to real assets in form of debt or equity commit¬ments.
Question 4.
___ is one who exercises any degree of discretion as to the investment or management of the portfolio of the securities or the funds of the client.
(A) Non-discretionary portfolio man¬ager
(B) Portfolio investor
(C) Discretionary portfolio manager
(D) Portfolio custodian
Answer:
(C) Discretionary portfolio manager
Question 5.
Return from listed security is in two forms ____
(A) One is interesting and the second is capital appreciation in price.
(B) One is the stock split and the second is the dividend.
(C) One is interesting and the second is a dividend.
(D) One is dividend and the second is capital appreciation in price.
Answer:
(D) One is dividend and the second is capital appreciation in price.
Question 6.
Which of the following is the correct formula to calculate returns of listed security?
(A) [(P1 – P0) + D] ÷ [P0 × 100]
(B) [(P1 – P0) + D] ÷ [P1 × 100]
(C) [(P1 – P0) – D] ÷ [P0 × 100]
(D) [(P1 – P0) + D(1 – t)] ÷ P0 × 100
Answer:
(A) [(P1 – P0) + D] ÷ [P0 × 100]
Question 7.
If the probability of occurrence is assigned, then the expected return would be:
(A) Average return being assigned to return of security for the various scenarios
(B) Weighted average of probabilities being assigned to return of security for the various scenarios
(C) Weighted average return with probabilities being assigned to return of security for the various scenarios
(D) Weighted average return mul¬tiplied by risk with probabilities being assigned to return of secu¬rity for the various scenarios
Answer:
(C) Weighted average return with probabilities being assigned to return of security for the various scenarios
Question 8.
Standard deviation is a deviation from –
(A) Arithmetic mean
(B) Harmonic mean
(C) Median mean
(D) Mode mean
Answer:
(A) Arithmetic mean
Question 9.
Standard deviation is expressed –
(A) Always in percentage
(B) In the same units in respect of which the deviation is computed.
(C) In terms of rupee risk
(D) In terms of the amount
Answer:
(B) In the same units in respect of which the deviation is computed.
Question 10.
The market price of a bond depends on _____
(A) The coupon rate and terms of the indenture
(B) The coupon rate and maturity date
(C) The terms of the indenture, and maturity date
(D) The coupon rate, terms of the indenture, and maturity date
Answer:
(D) The coupon rate, terms of the indenture, and maturity date
Question 11.
Investment with a lower standard deviation carries
(A) High risk
(B) Less risk
(C) Infinite risk
(D) Avoidable risk
Answer:
(B) Less risk
Question 12.
Which of the following is on the horizontal axis of the Security Market Line?
(A) Standard deviation
(B) Beta
(C) Expected return
(D) Required return
Answer:
(B) Beta
Question 13.
Covariance is a measurement of –
(A) The co-movement between two variables
(B) The link between the variability of returns in two independent securities
(C) Both (A) and (B)
(D) None of the above
Answer:
(C) Both (A) and (B)
Question 14.
Expected worth is the –
(A) Inverse of standard deviation
(B) Correlation between a security
(C) Same as a discrete probability distribution
(D) Weighted average of all possible outcomes
Answer:
(D) Weighted average of all possible outcomes
Question 15.
Positive Covariance indicates that –
(A) Returns on two assets bear a tendency to offset each other ie. if the return on A is above par, the return on B is likely to be below par. If the return on A is below par, the return on B is likely to be above par.
(B) There is no distinct relationship between the movements in re¬turns of two securities.
(C) Returns on two assets tend to go together, ie. if the return on A is above par, the return on B is also likely to be above par.
(D) Higher discount rate should be used in capital budgeting to dis¬count the cash flow.
Answer:
(C) Returns on two assets tend to go together, ie. if the return on A is above par, the return on B is also likely to be above par.
Question 16.
Liquidity risk:
(A) Is risk investments bankers face
(B) Is lower for small companies
(C) Is the risk associated with secondary market transactions
(D) Increases whenever interest rates increase
Answer:
(C) Is the risk associated with secondary market transactions
Question 17.
Correlation Coefficient supple¬ments and upgrades the –
(A) Expected return
(B) WACC
(C) Covariance
(D) Mean deviation
Answer:
(C) Covariance
Question 18.
Consider a graph with standard deviation on the horizontal axis and expected return on the vertical axis. The line that connects the risk-free rate and the optimal risky portfolio is called:
(A) Indifference curve
(B) The Capital market line
(C) Characteristic line
(D) Security market line
Answer:
(B) The Capital market line
Question 19.
A risk associated with project and way considered by a well-diversified stockholder is classified as –
(A) Expected risk
(B) Beta risk
(C) Industry risk
(D) Returning risk
Answer:
(B) Beta risk
Question 20.
Which of the following is the correct formula for the Correlation Coefficient?
(A) Covxy × σx × σy
(B) Covxy ÷ (σx × σy)
(C) (σx × σy) ÷ Covxy
(D) (σx ÷ σy ) × Covxy
Answer:
(B) Covxy ÷ (σx × σy)
Question 21.
An attempt to make a correction by adjusting historical beta to make it closer to an average beta is classified as –
(A) Adjusted stock
(B) Adjusted beta
(C) Adjusted coefficient
(D) Adjusted risk
Answer:
(B) Adjusted beta
Question 22.
The efficient frontier –
(A) Is the set of optimal portfolios that offers the highest expected return for a defined level of risk
(B) Is the set of optimal portfolios that offers the lowest risk for a given level of expected return
(C) Helps to decide whether new security can be selected or re¬jected
(D) All of the above
Answer:
(D) All of the above
Question 23.
A corporate bond is a corporation’s write undertaking that it will refund a specific amount of money plus –
(A) Premium
(B) Interest
(C) Nothing
(D) Security
Answer:
(B) Interest
Question 24.
The common stock of a company must provide a higher expected return than the debt of the same company because
(A) There is less demand for a stock than for bonds.
(B) There is greater demand for a stock than for bonds.
(C) There is more systematic risk involved for the common stock.
(D) There is a market premium re¬quired for bonds.
Answer:
(C) There is more systematic risk involved for the common stock.
Question 25.
As per the ‘Efficient Frontier’ concept, if the security falls below the frontier –
(A) The security is efficient and hence will be selected
(B) The security dominates some security on previously drawn security and hence the frontier itself will have to be re-draw
(C) The security is dominated by some security on the frontier and will be rejected.
(D) It shows that earning of the secu¬rity is above-market return and hence will be selected
Answer:
(C) The security is dominated by some security on the frontier and will be rejected.
Question 26.
The advocates of the Efficient-market hypothesis (EMH) theory contend that securities markets are –
(A) Perfect
(B) Imperfect
(C) Monopolistic
(D) Perfect or at least not too imperfect.
Answer:
(D) Perfect or at least not too imperfect.
Question 27.
The EMH was developed by Professor Eugene Fama who argued that –
(A) Stocks always trade at their fair value, making it impossible for investors to either purchase undervalued stocks or sell stocks for inflated prices.
(B) It should be impossible to outperform the overall market through expert stock selection or market timing, and that the only way an investor can possibly obtain higher returns is by chance or by purchasing riskier investments
(C) Efficient capital markets prices of traded securities always ful¬ly reflect all publicly available information concerning those securities
(D) All of the above
Answer:
(D) All of the above
Question 28.
Dow Jones theory was formulated by-
(A) John P. Dow
(B) Charles H. Dow
(C) James T. Dow
(D) Michel R. Dow
Answer:
(B) Charles H. Dow
Question 29.
According to Dow Jones theory, share prices demonstrate a pattern over 4 to 5 years. These patterns can be divided into three distinct cyclical trends –
(A) Preliminary, primary and sec¬ondary trends
(B) Preliminary, bullish and bearish trends
(C) Primary, secondary and minor trends
(D) Primary, secondary and major trends.
Answer:
(C) Primary, secondary and minor trends
Question 30.
____ suggests that stock price changes have the same distribution and are independent of each other, so the past movement or trend of a stock price or market cannot be used to predict its future movement.
(A) Technical analysis theory
(B) Random walk theory
(C) Efficient market theory
(D) Fundamental Market theory
Answer:
(B) Random walk theory
Question 31.
According to the Sharpe single index model, the return for each security can be given by the –
(A) αI + βI + E
(B) αI × βI × E
(C) αI ÷ βI ÷ E
(D) αI – βI – E
Answer:
(A) αI + βI + E
Question 32.
The covariance between Security X and Security Y is zero. This indicates that –
(A) There is a strong relationship between the movements in returns of two securities.
(B) There is a positive relationship between the movements in returns of two securities.
(C) There is no distinct relationship between the movements in returns of two securities.
(D) There is a negative relationship between the movements in returns of two securities.
Answer:
(C) There is no distinct relationship between the movements in returns of two securities.
Question 33.
Following details are available for two securities:
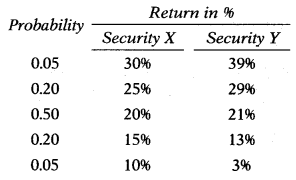
Calculate the expected return.

Hint:
X: (0.05 × 30) + (0.20 × 25) + (0.50 × 20) + (0.20 × 15) + (0.05 × 10) = 20%
Y: (0.05 × 39) + (0.20 × 29) + (0.50 × 21) + (0.20 × 13) + (0.05 × 3) = 21%
Answer:
(C)
Question 34.
You have been given the following data for Security X:
| Probability | Return |
| 0.05 | 7% |
| 0.20 | 10% |
| 0.50 | 13.5% |
| 0.20 | 17% |
| 0.05 | 20% |
Calculate the standard deviation of security.
(A) 3.02%
(B) 3.36%
(C) 4.57%
(D) 4.12%
Hint:

Answer:
(A) 3.02%
Question 35.
Following details are available for EX Ltd. & FX Ltd. securities.
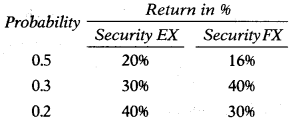
Covariance between Security EX and Security FX is –
(A) 85
(B) 58
(C) -58
(D) – 54
Hint:
Expected returns: EX Ltd. = 27%; FX Ltd. = 26%

Answer:
(B) 58
Question 36.
The covariance between Security X and Security Y is + 45.8. This indicates that –
(A) If the return on Security X is below par, return on Security Y is likely to be above par.
(B) Returns on Security X& Security Y tend to go together, ie. if the return on X is above par, the return on Y is also likely to be above par.
(C) Returns on Security X & Security Y bear a tendency to offset each other.
(D) Covariance of these to two securities is positive which means the standard deviation of both securities must be negative.
Answer:
(B) Returns on Security X & Security Y tend to go together, ie. if the return on X is above par, the return on Y is also likely to be above par.
Question 37.
The covariance between Security X and security Y is – 42. This indicates that –
(A) Returns on Security X& Security Y bear a tendency to offset each other.
(B) Covariance of these to two securities is negative which means the standard deviation of both securities must be positive.
(C) There is no distinct relation between Security X and Security Y.
(D) Return on Security X is above par, return on Security Y is also likely to be above par.
Answer:
(A) Returns on Security X& Security Y bear a tendency to offset each other.
Question 38.
The covariance between Security P&Q § is 48.91. The standard deviation of Security P is 5.36 while that of Security Q is g 9.13. Compute the value of the correlation coefficient.
(A) 0
(B) 1
(C) -1
(D) 0.899
Hint:
CorrPQ = \(\frac{\operatorname{Cov}_{\mathrm{PQ}}}{\sigma_{\mathrm{P}} \times \sigma_{\mathrm{Q}}}=\frac{48.91}{5.36 \times 9.13}=\frac{48.91}{48.94}\) = 0.9994 i.e. 1.
Answer:
(B) 1
Question 39.
An investor has invested in Security A & B in the ratio of 70:30. The standard deviation of Security A & B is 4.47 & 7.62 respectively. Covariance AB is 34. The Correlation Coefficient of Security A & B is 1. Risk of the portfolio is –
(A) 5.41%
(B) 6.48%
(C) 3.13%
(D) 7.26%
Hint:
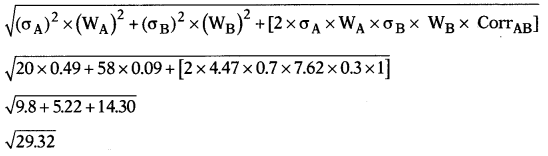
Portfolio risk = σ = 5.41%
An alternative way to calculate portfolio risk.

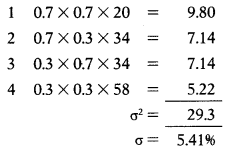
Answer:
(A) 5.41%
Question 40.
X and Y are two securities in the portfolio for which the following information is available.
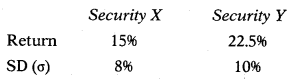
Correlation coefficient is + 0.7.
What weight you will assign to the Security Y so that portfolio risk is lowest?
(A) 15.38%
(B) 84.62%
(C) 82.46%
(D) 20.18%
Hint:
Covariance = Corr × σx × σy
= 0.7 × 8 × 10
= 56
Wx = \(\frac{\left(\sigma_{x}\right)^{2}-\operatorname{Cov}_{x y}}{\left(\sigma_{x}\right)^{2}+\left(\sigma_{y}\right)^{2}-2 \times \operatorname{Cov}_{x y}}\)
= \(\frac{64-56}{64+100-2 \times 56}\)
= \(\frac{8}{52}\)
= 0.1538 i.e. 15.38% (Weight of Security X)
Answer:
(B) 84.62%
Question 41.
Suppose the risk-free rate is 4% and X is 2.5%. If an investor takes 13% risk, he can expect a return of –
(A) 32.5%
(B) 52%
(C) 10%
(D) 36.5%
Hint:
The risk-free rate is 4% and k is 2.5%. Thus, for every 1% increase in the risk, the investor can expect a 2.5% above risk-free return. Thus, if an investor takes a 13% risk, he can expect a return of 36.5% (13 × 2.5 + 4).
Answer:
(D) 36.5%
Question 42.
Yogesh invests ₹ 1,25,000 in shares of BABA Ltd., a listed company. At the end of the period investment value is ₹ 1,32,000. He gets a dividend of ₹ 8,000. Return from investment is –
(A) 11%
(B) 12%
(C) 13%
(D) 14%
Hint:
[(1,32,000 – 1,25,000) + 8,000]/1,25,000 = 12%
Answer:
(B) 12%
Question 43.
The following data is available for two listed securities:
Covrb = 37
σb = 8.49%
The correlation coefficient between security R and Security B is +0.8595. The standard deviation of Security R should have been –
(A) 4.03%
(B) 8.04%
(C) 5.07%
(D) 6.09%
Hint:
Covariance = Corrb × σr × σb
37 = 0.8595 × σr × 8.49
37 = 7.297 × σr
σr = 5.07
Answer:
(C) 5.07%
Question 44.
The actual return of GK Ltd. for the last four years is 20%, 14%, 17%, and 18%. GK Ltd. has a beta of 1.15. Return on the market portfolio is 15%. The risk-free rate of return is 6%. Compute Alpha value and decide whether to hold, buy or sell the security?
(A) Alpha value is +0.8 and hence it is advised to sell the security.
(B) Alpha value is -0.9 and hence it is advised to buy the security.
(C) Alpha value is -0.8 and hence it is advised to short sell the security
(D) Alpha value is +0.9 and hence it is advised to buy the security.
Hint:
ER = Rf + β (Rm – Rf)
= 6+ 1.15(15 – 6)
= 16.35%
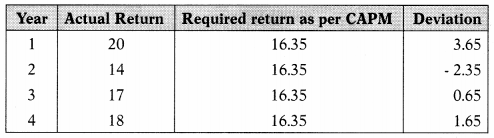
= \(\frac{3.65-2.35+0.65+1.65}{4}\) = 0.9
Answer:
(D) Alpha value is +0.9 and hence it is advised to buy the security.
Question 45.
Return of last 5 years of listed security is 16.2%, 19.8%, 18%, 15% & 21%. Five years ago the price of the security was 120 per share. What is its average return?
(A) 18%
(B) 19%
(C) 20%
(D) 21%
Answer:
(A) 18%
Question 46.
Return of last 5 years of listed security is 16.2%, 19.8%, 18%, 15% & 21%. Five years ago the price of the security was 120 per share.
What is its holding period return?
(A) 135.55% .
(B) 128.58%
(C) 145.64%
(D) 154.45%
Hint:
120 × 1.162 × 1.198 × 1.18 × 1.15 × 1.21 = 274.29
(274.29 – 120)/120 × 100 = 128.58%
Answer:
(B) 128.58%
Question 47.
Dividend for the last 4 years of Tara Ltd. was ₹ 7, ₹ 5, 12.8 & ₹ 10, and the market price was ₹ 120, ₹ 80, ₹ 130 & ₹ 150 respectively. What is the average return of the last 3 years considering capital gain and dividend?
(A) 19.28%
(B) 14.48%
(C) 10.84%
(D) 16.65%
Hint:
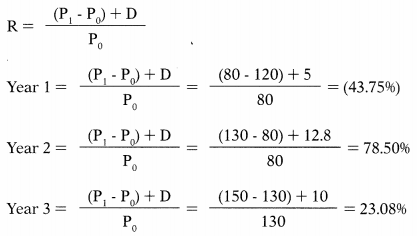
Average return = – 43.75 + 78.50 + 23.08/3 = 19.28%
Answer:
(A) 19.28%
Question 48.
Given the probability of 0.1,0.4,0.3 & 0.2 estimated returns of the security are 36%, 26%, 20% & 15% respectively. Risk free rate is 6% and cost of capital is 13%. Total risk of security is –
(A) 36%
(B) 12%
(C) 6%
(D) 4%
Hint:
Expected Return = 23%
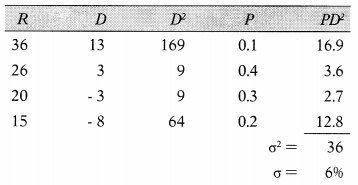
Answer:
(C) 6%
Question 49.
From the following data, you are required to calculate the covariance of Security G and Security K and interpret the result.
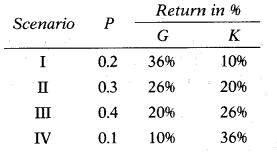
Select the correct answer from the options given below.
(A) Covariance between Security G& Security K is +56 which indicates that return on these two securities tends to go together.
(B) Covariance between Security G& Security K is -48 which indicates that return on these two securities bears a tendency to offset each other.
(C) Covariance between Security G& Security K is +48 which indicates that return on these two securities tends to go together.
(D) Covariance between Security G& Security K is -56 which indicate that return on these two securities bear tendency to off-set each other
Hint:
Expected Return: Security G = 24; Security K = 22
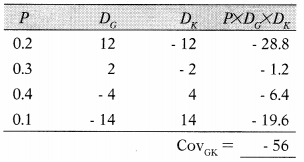
Answer:
(D) Covariance between Security G& Security K is -56 which indicate that return on these two securities bear tendency to off-set each other
Question 50.
The following data is available for the Security P & Q.

Correlation Coefficient for the above two securities is –
(A) -0.9899
(B) -0.9989
(C) +0.8999
(D) +0.9989
Hint:
The expected return of both securities is 10% and both securities have the same probabilities for the returns hence standard deviation for both the securities will be the same as shown below.
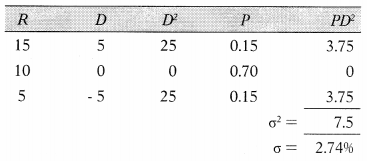

CorrPQ = \(\frac{\mathrm{Cov}_{\mathrm{PQ}}}{\sigma_{\mathrm{p}} \times \sigma_{\mathrm{Q}}}=\frac{-7.5}{2.74 \times 2.74}=\frac{-7.5}{7.5076}\) = – 0.9989
Answer:
(B) -0.9989
Question 51.
The expected return of Security A is 20% while that of Security B is 25%. The beta of Security A is 0.85 while that of Security B is 1.25. What is the market rate of return?
(A) 21.875%
(B) 22.385%
(C) 18.655%
(D) 20.555%
Hint:
Let the be Rf ‘x’ and (Rm – Rf) be ‘y’
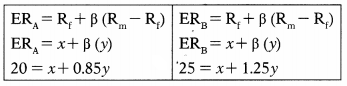
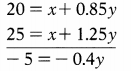
y = 5/0.4 = 12.5
y = Rm – Rf = 12.5
Putting value of V in first equation we can get value of ‘x’.
20 = x + 0.85y
20 = x + 0.85 × 12.5
20 = x + 10.625
x = Risk free rate = 9.375%
Calculation market rate of return:
Rm – Rf = 12.5
Rm – 9.375 = 12.5
Rm =21.875%
Answer:
(A) 21.875%
Question 52.
The expected return and beta of the three securities are as follows:
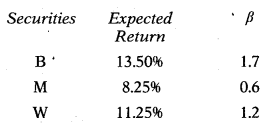
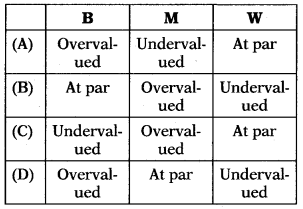
If the risk-free rate of return is 6.75% and the expected return on the market portfolio is 10.5%, which of the above securities under or correctly valued?
Hint:
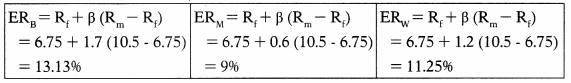
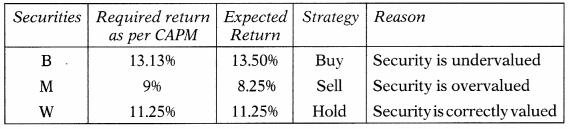
Answer:
(C)
Question 53.
The actual return of T Ltd. for the last four year is as follows:
| Year | Return |
| 1 | 15.06% |
| 2 | 10.12% |
| 3 | 12.28% |
| 4 | 13.26% |
T Ltd. has a beta of 1.15. Return on the market portfolio is 11.2%. The risk-free rate of return is 4%. Compute Alpha value and decide whether to hold, buy, or sell the security.
(A) Alpha value is positive i.e. 0.4 and hence security is overvalued. Such security should be sold.
(B) Alpha value is positive ie. 0.4 and hence security is undervalued. Such security should be bought.
(C) Alpha value is negative le. – 0.2 and hence security is overvalued. Such security should be sold.
(D) Alpha value is negative ie. – 0.2 and hence security is undervalued. Such security should be bought.
Hint:
ER = Rf + β(Rm – Rf)
= 4 + 1.15(11.2 – 4)
= 12.28%
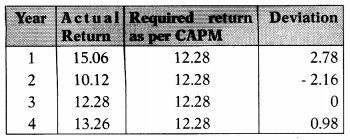
= \(\frac{2.78-2.16+0+0.98}{4}\) = 0.4
Alpha value is positive i.e. 0.4 and hence security is undervalued. Such security should be bought.
Answer:
(B) Alpha value is positive ie. 0.4 and hence security is undervalued. Such security should be bought.
Question 54.
The following details are made available to you for security.
Beta (β): 1.4
The risk-free rate of return: 6.3%
The market rate of return: 13.2%
If the alpha value is + 1.8 what investment action would you suggest?
(A) Buy
(B) Hold
(C) Sell
(D) Short
Hint:
ER = Rf + β (Rm – Rf)
ER = 6.3 + 1.4 (13.2 – 6.3)
ER = 15.96%
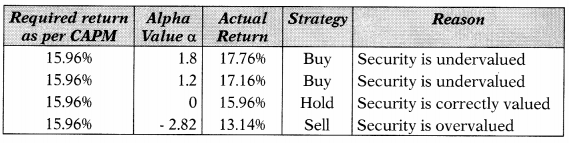
Answer:
(A) Buy
Question 55.
The following details are made available to you for security.
Beta (β): 1.4
The risk-free rate of return: 6.3%
The market rate of return: 13.2%
If the alpha value is + 1.2 what investment action would you suggest?
(A) Short
(B) Sell
(C) Buy
(D) Hold
Hint:
ER = Rf + β (Rm – Rf)
ER= 6.3 + 1.4 (13.2 – 6.3)
ER= 15.96%

Answer:
(C) Buy
Question 56.
The following details are made available to you for security.
Beta (p) : 1.4
Risk-free rate of return: 6.3%
Market rate of return: 13.2%
If the alpha value is zero what investment action would you suggest?
(A) Buy as Security is undervalued.
(B) Sell as Security is undervalued.
(C) Hold as Security is correctly valued.
(D) Sell as Security is overvalued.
Hint:
ER = Rf + β (Rm – Rf)
ER= 6.3 + 1.4 (13.2 – 6.3)
ER= 15.96%

Answer:
(C) Hold as Security is correctly valued.
Question 57.
The following details are made available to you for security.
Beta (P): 1.4
The risk-free rate of return: 6.396
The market rate of return: 13.296
If the alpha value is negative i.e. – 2.82 what investment action would you suggest?
(A) Hold
(B) Buy
(C) Sell
(D) None of the above
Hint:
ER = Rf + β (Rm – Rf)
ER= 6.3 + 1.4 (13.2 – 6.3)
ER= 15.96%

Answer:
(C) Sell
Question 58.
Stocks A & B have the following historical returns:
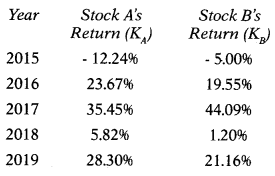
Assume that someone held a portfolio consisting of 70% of Stock A and 30% of Stock B. What would have been the realized rate of return on the portfolio in each year from 2015 to 2019?
(A) 16.20%
(B) 15.40%
(C) 18.60%
(D) 13.70%
Hint:
Stock A = \(\frac{-12.24+23.67+35.45+5.82+28.30}{5}\) = 16.20%
Stock B = \(\frac{-5+19.55+44.09+1.20+21.60}{5}\) = 16.20%
(16.20 × 0.7) + (16.20 × 0.3) = 16.20%
Answer:
(A) 16.20%
Question 59.
Following details are gathered by the investor:
Standard deviation 2.8%
Market standard deviation 2.3%
The risk-free rate of return 8%
Expected rate of return on market portfolio 18%
The correlation coefficient of the portfolio with a market of 0.8
The required return on a security is –
(A) 14.77%
(B) 17.74%
(C) 15.84%
(D) 20.65%
Hint:
β = \(\frac{\sigma_{\mathrm{s}}}{\sigma_{\mathrm{M}}}\) × CorSM = \(\frac{2.8}{2.3}\) × 0.8 = 0.974
Calculation of required return on the security:
ER = Rf + β (Rm – Rf)
= 8 + 0.974(18 – 8)
= 17.74%
Answer:
(B) 17.74%
Question 60.
Following details are made available to you for particular security:
The beta of security: 0.5
Expected return on portfolio: 15%
The risk-free rate of return: 0.06
In another security has an expected rate of return of 18%, what would be its beta?
(A) 1.222
(B) 1.111
(C) 1.333
(D) 1.444
Hint:
ER = Rf + β (Rm – Rt)
= 6 + 0.5(15 – 6) .
= 10.5%
Computation of beta for other security:
ER = Rf + β (Rm – Rf)
18 = 6 + β (15 – 6)
18 = 6 + 9β
12 = 9β
β = 1.3333
Answer:
(C) 1.333
