This Ratio and Proportion – CA Foundation Maths Study Material is designed strictly as per the latest syllabus and exam pattern.
Ratio and Proportion – CA Foundation Maths Study Material
Ratio:
The comparison of two or more things of same kind is called Ratio. If x and y are two values of same kind (in same units), then the ratio of x to y is written as x : y and read as x is to y.
In \(\frac{x}{y}\)
- Numerator “x” is called 1st term or Antecedent and
- Denominator “y” is called 2nd term or Consequent.
- Antecedent and Consequent must be of same units
- Ratio has no unit.
Remarks:
- Normally a ratio is expressed in simplest form. As. 10:16 = 5:8.
- The order of the terms in a ratio must be maintained. As 3 : 4 is not same as 4:
- Ratio exists only with quantities having same unit (kind).
- If x > y, then the ratio x : y is called of greater inequality.
- If x < y, then the ratio x : y is called of lesser inequality.
- If x = y, then the ratio a : b is called ratio of Equal Equality.
- Duplicate ratio of a : b is a2: b2
- Triplicate ratio of a : b is a3 : b3
- Sub-Duplicate ratio of a : b is √a : √b = a1/2 : b1/2
- Sub-Triplicate ratio of a : b is 3√a ; 3√b = a1/3 : b1/3
- Inverse ratio of x : y is y : x.
- Commensurable: If the terms of the ratio are integers, the ratio is called commensurable. As. 3 :2
- Incommensurable : If the terms of the ratio are not integers, the ratio is called Incommensurable.
As √3 : √2 cannot be expressed in terms of integers. So, it is Incom-mensurable.
- Compound/Combined Ratio = Product of all ratios.
Proportion:
An equality of two ratios is called Proportion. Four quantities a, b, c, d are said to be in proportion if a : b = c : d.
It is also written as
a : b : : c : d
Here a, b, c, d are called 1st; 2nd; 3rd and 4th term of proportionals respectively a c
If \(\frac{a}{b}=\frac{c}{d}\) ⇒ ad = bc.
Product of extreme terms = Product of middle terms.
This rule is called Cross – Product Rule.
In a: b :: c : d. proportion, unit of a and b should be same and that of c and d should also be same.
As. ₹ 6 : ₹ 8 = 12 toffees : 16 toffees are in proportion.
Let a, b and c are of same kind (in same units). a b
If \(\frac{a}{b}=\frac{b}{c}\) ⇒ a : b : : b : c
i. e. a, b, c are in proportion. ‘
Then, this proportion is called continuous proportion.
Here a is 1st proportion c is called 3rd proportion and b is called mean proportion.
b = \(\sqrt{a c}\) = GM of a & c.
![]()
Properties of Proportion
1. Cross-Product
If a : b : : c : d.
⇒ \(\frac{a}{b}=\frac{c}{d}\) ∴ ad = be.
2. Invertendo
If a : b : : c : d.; Then its inverse
b : a :: d : c also becomes in proportion.
i.e. If \(\frac{a}{b}=\frac{c}{d}\) Then, \(\frac{b}{a}=\frac{d}{c}\)
3. Componendo
If a : b :: c : d.
Then a + b:b::c + d:d.
Proof \(\frac{a}{b}+1=\frac{c}{d}+1 \Rightarrow \frac{a+b}{b}=\frac{c+d}{d}\)
4. Dividendo
If a : b = c : d.
Then a – b : b = c – d : d.
Proof: \(\frac{a}{b}=\frac{c}{d} \Rightarrow \frac{a}{b}-1=\frac{c}{d}-1\)
or \(\frac{a-b}{b}=\frac{c-d}{d}\)
5. Componendo and Dividendo
If a : b : : c : d. ; Dividing (3) by (4)
Then, \(\frac{a+b}{a-b}=\frac{c+d}{c-d}\)
6. Alternendo:
If a : b : : c : d
Then a : c : : b : d
i.e ratio of alternate terms are also in proportion.
7. Addendo
If a : b = c : d = e : f = …………………
Then each ratio = \(\frac{\text { Sum of antecedents of all ratios }}{\text { Sum of consequents of all ratios }}\)
∴ \(\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\ldots \ldots \ldots .=\frac{a+c+e+\ldots \ldots}{b+d+f+\ldots}\)
8. Subtrahendo
If \(\frac{a}{b}=\frac{c}{d}=\frac{e}{f}\) = ……….
Then each ratio
∴ \(=\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\ldots \ldots \ldots .=\frac{a-c-e-\ldots .}{b-d-f-\ldots .}\)
Previous Year Exam Questions
Question 1.
Two numbers are in the ratio of 2 : 3 and the difference of their squares is 320. The number are : [1 Mark, Nov. 2006]
(a) 12, 18
(b) 16, 24
(c) 14, 21
(d) None
Answer:
Tricks : Go by choices (a); (b) & (c) all are in ratio 2:3 But For option
(a) 182 – 122 ≠ 320
(b) 242 – 162 = (24+ 16) (24 – 16)
= 40 × 8 = 320
Question 2.
If p : q is the sub-duplicate ratio of p – x2: q – x2, then x2 is : [1 Mark, Nov. 2006]
(a) \(\frac{p}{p+q}\)
(b) \(\frac{q}{p+q}\)
(c) \(\frac{q p}{p-q}\)
(d) None
Answer:
Detail Method:
\(\frac{\sqrt{p-x^2}}{\sqrt{q-x^2}}=\frac{p}{q}\)
Squaring on both side; we get
\(\frac{p-x^2}{q-x^2}=\frac{p^2}{q^2}\)
or pq2 – q2x2 = p2q – p2x2
or p2x2 – q2x2 = p2q – pq2
or x2(p2 – q2) = pq(p – q)
or x2 (p + q)(p-q) = pq (p – q)
(d) is correct
Tricks : Go by choices.
Question 3.
An alloy is to contain copper and zinc in the ratio 9:4. The zinc required to melt with 24 kg of copper is : [1 Mark, Nov. 2006]
(a) 10\(\frac{2}{3}\)kg
(b) 10\(\frac{1}{3}\)kg
(c) 9\(\frac{2}{3}\)kg
(d) 9 kg
Answer:
Let Zinc = x kg
(a) ∴ \(\frac{9}{4}=\frac{24}{x}\) ∴ x = \(\frac{4 \times 24}{9}=\frac{32}{3}\)
= 10\(\frac{2}{3}\)kg
∴ (a) is correct
Question 4.
Two numbers are in the ratio 7: 8. If 3 is added to each of them, their ratio becomes 8 : 9. The numbers are: [1 Mark, Feb. 2007]
(a) 14,16
(b) 24,27
(c) 21,24
(d) 16,18
Answer:
Tricks : Go by choices
(b) and (d) are not in the ratio 7 : 8 So (b) & (d) are not answer For (a) it is added then
\(\frac{14+3}{10+3}=\frac{17}{19} \neq \frac{8}{9}\)
(a) is not answer
(c) is answer Detail Method:
Let x is common in the ratio
∴ Numbers are 7x & 8x
Now \(\frac{7 x+3}{8 x+3}=\frac{8}{9}\)
or 64x + 24 = 63x + 27
or 64x – 63x = 27-24
or x = 3
1st number = ix = 7×3 = 21
2nd number = 8x = 8×3 = 24
(c) is correct
![]()
Question 5.
A box contains ₹ 56 in the form of coins of one rupee, 50 paise and 25 paise. The number of 50 paise coin is double the number of 25 paise coins and four times the numbers of one rupee coins. The numbers of 50 paise coins in the box is : [1 Mark, Feb. 2007]
(a) 64
(b) 32
(c) 16
(d) 14
Answer:
Tricks : Go by choices
No. of 25 paise coins = \(\frac{1}{2}\) No. of 50 Paise
No. of Rupee coins = \(\frac{1}{4}\) No. of 50 Paise Coins
For (a) No. of coins of ₹ 1;50 Paise & 25 Paise
\(\frac{64}{4}\); 64; \(\frac{64}{2}\)
Total Value = 16 × 1 + 64 × 0.50 + 32 × 0.25
= ₹ 16 + 32 + 8 = ₹ 56
Which is equal to given value (a) is Correct
Detail Method
Let No. of 50 Paise coins = x
∴ No. of ₹ 1 coins = \(\frac{x}{4}\)
and No. of 25 Paise coins = \(\frac{x}{2}\)
∴ Total Value =
\(\frac{x}{4}\) × 1 + x × 0.50+ \(\frac{x}{2}\) × 0.25 = 56
or 0.25x + 0.50x + 0.125x
or 0.875x = 56
or x = \(\frac{56}{0.875}\) = 64
∴ (a) is correct
Question 6.
Eight people are planning to share equally the cost of a rental car. If one person withdraws from the arrangement and the others share equally entire cost of the car, then the share of each of the remaining persons increased by : [1 Mark, May 2007]
(a) 1/9
(b) 1/8
(c) 1/7
(d) 7/8
Answer:
Tricks : Per Person share increase = \(\frac{1}{7}\) of total share
Question 7.
A bag contains ₹ 187 in the form of 1 rupee, 50 paise and 10 paise coins in the ratio 3:4:5. Find the number of each type of coins: [1 Mark, May 2007]
(a) 102, 136, 170
(b) 136, 102, 170
(c) 170, 102, 136
(d) None
Answer:
Tricks I: Go by choices
For (a) Coins are in the ratio 3:4:5
∴ \(\frac{102}{3}=\frac{136}{4}=\frac{170}{5}\) = 34
It satisfies 1st condition
Now 102 × 1 + 136 × 0.50 + 170 × 0.10
= 102 + 68 + 17 = ₹ 187
∴ (a) is correct
Tricks II
Common factor = \(\frac{187}{3 \times 1+4 \times 0.50+5 \times 0.10}\)
= \(\frac{187}{5.50}\) = 34
∴ No. of 1 Rupee coins =3 × 34 = 102
No. of 50 Paise coins =4 × 34 = 136
No. of 10 paise coins = 5 × 34 = 170 (a) is correct
Detail Method
Let x is common in the ratio
No. of 1 Rupee ; 50 Paise and 10 Paise Coins are 3x ; 4x and 5x
∴ 3x × 1 + 4x × 0.50 + 5x × 0.10 = 187
or 5.50x = 187
∴ x = \(\frac{187}{5.50}\) = 34
∴ No. of 1 Rupee coins = 3x = 3 × 34 = 102
No. of 50 Paise coins = 4x = 4 × 34 = 136
No. of 10 Paise coins = 5x = 5 × 34 = 170
∴ (a) is correct
Question 8.
Ratio of earnings of A and B is 4 : 7. If the earnings of A increase by 50% and those of B decrease by 25%, the new ratio of their earning becomes 8 : 7. What is A’s earning ?
(a) ₹ 21,000
(b) ₹ 26,000
(c) ₹ 28,000
(d) Data inadequate [1 Mark, Aug. 2007]
Answer:
Detailed Method Let x is common in the ratio
∴ A’s and B’s present earnings are 4x and 7x respectively
From question \(\frac{4 x+4 x \times 0.50}{7 x-7 x \times 0.25}=\frac{8}{7}\)
or \(\frac{6 x}{5.25 x}=\frac{8}{7}\)
x cannot be found.
Data is inadequate
∴ (d) is Correct
Question 9.
P, Q and R are three cities. The ratio of average temperature between P and Q is 11 : 12 and that of between P and R is 9: 8. The ratio between the average temperature of Q and R is : [1 Mark, Aug. 2007]
(a) 22: 27
(b) 27: 22
(c) 32: 33
(d) None
Answer:
∴ P: Q= 11 : 12 ∴ Q :P= 12 : 11
\(\frac{Q}{P} \times \frac{P}{R}=\frac{12}{11} \times \frac{9}{8}\)
\(\frac{Q}{R}=\frac{27}{22}\) Q :P= 12 : 11
(b) is Correct
Question 10.
₹ 407 are to be divided among A, B and C so that their shares are in the ratio \(\frac{1}{4}: \frac{1}{5}: \frac{1}{6}\)
The respective shares of A, B, C are: [1 Mark, Nov. 2007]
(a) ₹ 165, ₹ 132, ₹ 110
(b) ₹ 165, ₹ 110, ₹ 132
(c) ₹ 132, ₹ 110, ₹ 165
(d) ₹ 110, ₹ 132, ₹ 165.
Answer:
A:B:C = \(\frac{1}{4}: \frac{1}{5}: \frac{1}{6}\) × LCM of denominators = 60
= 15 : 12 : 10
∴ A’s share = \(\frac{407}{15+12+10}\) × 15 = Rs. 165
B’s share = \(\frac{407}{37}\) × 12 = Rs. 132
C’s share = \(\frac{407}{37}\)× 10 = Rs. 110
(a) is Correct
Tricks : Go by Choices.
Question 11.
The incomes of A and B are in the ratio 3 :2 and their expenditures in the ratio 5 : 3. If each saves ₹ 1,500, then B’s income is : [1 Mark, Nov. 2007]
(a) ₹ 6,000
(b) ₹ 4,500
(c) ₹ 3,000
(d) ₹ 7,500
Answer:
Detail Method Let x is common in the ratio.
A’s income = 3x
B’s income = 2x
∴ \(\frac{3 x-1500}{2 x-1500}=\frac{5}{3}\)
or 10x – 7500 = 9x – 4500
or 10x – 9x = 7500 – 4500
or x = 3000
B’s income = 2x =2 × 3000
= ₹ 6000.
(a) is Correct Tricks : Go by choices For (a)
\(\frac{A}{B}\) Expenditure = \(\frac{\frac{6000}{2} \times 3-1500}{6000-1500}=\frac{7500}{4500}=\frac{5}{3}\)
(a) is Correct
![]()
Question 12.
In 40 litres mixture of glycerine and water, the ratio of glycerine and water is 3:1. The quantity of water added in the mixture in order to make this ratio 2:1 is : [1 Mark, Feb. 2008 ]
(a) 15 litres
(b) 10 litres
(c) 8 litres
(d) 5 litres
Answer:
Glycerine = \(\frac{40}{3+1}\) x 3 = 30 litres.
Water = \(\frac{40}{4}\) x 1 = 10 litres 4
Let x litres of water is added to the mixture
Then \(\frac{30}{10+x}=\frac{2}{1}\)
or, 2x + 20 = 30
or x = 5
∴ (d) is Correct
Tricks : Go by Choices
Question 13.
The third proportional between (a2 – b2) and (a + b)2 is : [1 Mark, Feb. 2008]
(a) \(\frac{a+b}{a-b}\)
(b) \(\frac{a-b}{a+b}\)
(c) \(\frac{(a-b)^2}{a+b}\)
(d) \(\frac{(a+b)^3}{a-b}\)
Answer:
3rd Proportion = \(\frac{(\text { Mean prop. })^2}{\text { lst Proportional }}\)
= \(\frac{\left\{(a+b)^2\right\}^2}{a^2-b^2}=\frac{(a+b)^4}{3(a+b)(a+b)}=\frac{(a+b)^3}{a-b}\)
(d) is Correct
Question 14.
In what ratio should tea worth ₹ 10 per kg. be mixed with tea worth ₹ 14 per kg., so that the average price of the mixture may be ₹ 11 per kg.? [1 Mark, June 2008]
(a) 2 : 1
(b) 3 : 1
(c) 3 : 2
(d) 4 : 3
Answer:
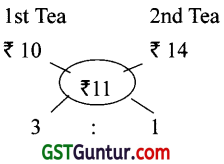
∴ (b) is Correct
Question 15.
The ages of two persons are in the ratio 5:7. Eighteen years ago their ages were in the ratio of 8:13, their present ages (in years) are : [1 Mark, June 2008]
(a) 50; 70
(b) 70,50
(c) 40,56
(d) None
Answer:
Tricks : Go by choices (a) & (c) are in the ratio 5 : 7 not (b)
For (a) 18 year ago
So, (a) is Correct
Question 16.
If A, B and C started a business by investing ₹ 1,26,000, ₹ 84,000 and ₹ 2,10,000. If at the end of the year profit is ₹ 2,42,000 then the share of each is : [1 Mark, Dec. 2008]
(a) ₹ 72,600; ₹ 48,400 ; ₹ 1,21,000
(b) ₹ 48,400 ; ₹ 1,21,000 ; ₹ 72,600
(c) ₹ 72,000 ; ₹ 49,000 ; ₹ 1,21,000
(d) ₹ 48,000 ; ₹ 1,21,400 ; ₹ 72,600
Answer:
Investment ratio is
A : B : C = 126,000 : 84,000 : 2,10,000 ÷ 14,000
= 9: 6 : 15 ÷ 3
= 3: 2: 5
A’s share = \(\frac{₹ 242,000}{3+2+5}\) × 3 =₹ 72, 600
B’s share = \(\frac{242,000}{20}\) × 2 = ₹48, 400
C’s share = \(\frac{242000}{10}\) × 5 = ₹ 1,21,000
So, (a) is Correct
Question 17.
If \(\frac{p}{q}=-\frac{2}{3}\) then the value of \(\frac{2 p+q}{2 p-q}\) is: [1 Mark, June 2009]
(a) 1
(b) \(-\frac{1}{7}\)
(c) \(\frac{1}{7}\)
(d) 7
Answer:
∵ \(\frac{p}{q}=\frac{-2}{3}\)
Tricks
\(\frac{2 p+q}{20-q}=\frac{2(-2)+3}{2(-2)-3}=\frac{-4+3}{-4-3}=\frac{-1}{-7}=\frac{1}{7}\)
(c) is correct
Question 18.
Fourth proportional to x, 2x, (x +1) is :
(a) x + 2
(b) (x + 2)
(c) (2x + 2)
(d) (2x – 2)
Answer:
Let Fourth Proportional is K.
∴ \(\frac{x}{2 x}=\frac{x+1}{K}\)
or k.x = 2x (x + 1)
or k = 2 (x + 1) = 2x +2
(c) is correct
![]()
Question 19.
What must be added to each term of the ratio 49 : 68 so that it becomes 3 : 4? [1 Mark, June 2010]
(a) 3
(b) 5
(c) 8
(d) 9
Answer:
Detail Method:
Let x is added to each term
Then \(\frac{49+x}{68+x}=\frac{3}{4}\)
or 196 +4x = 204 + 3x
or 4x – 3x = 204 – 196
or x = 8
(c) is Correct
Tricks : Go by Choices
1st Find \(\frac{3}{4}\) = 0.75 (By Calculator)

Question 20.
The students of two classes are in the ratios 5 : 7, if 10 students left from each class, the remaining students are in the ratio of 4 : 6, then the number of students in each class was : [1 Mark, June 2010]
(a) 30, 40
(b) 25, 24
(c) 40, 60
(d) 50, 70
Answer:
Tricks : Go by choices:
(a); (b) and (c) are not in the ratio 5 : 7
∴ (d) is Correct.
Question 21.
If A: B= 2: 5, then (10A + 3B) : (5A + 2B) is equal to: [1 Mark, Dec. 2010]
(a) 7: 4
(b) 7: 3
(c) 6: 5
(d) 7: 9
Answer:
It A : B = 2 : 5 Then
\(\frac{10 A+3 B}{5 A+2 B}=\frac{10 \times 2+3 \times 5}{5 \times 2+2 \times 5}=\frac{35}{20}=\frac{7}{4}\)
= 7: 4
(a) is Correct
Question 22.
In a film shooting, A and B received money in a certain ratio and B and C also received the money in the same ratio. If A gets ₹ 1,60,000 and C gets ₹ 2,50,000. Find the amount received by B ? [1 Mark, June 2011]
(a) ₹ 2,00,000
(b) ₹ 2,50,000
(c) ₹ 1,00,000
(d) ₹ 1,50,000
Answer:
Detail Method
A : B = B : C
So, B2 = AC ;
so, B = \(\sqrt{\mathrm{AC}}=\sqrt{1,60,000 \times 2,50,000}\)
= 400 × 500 = 2,00,000
Question 23.
The ratio compounded of 4:5 and sub-duplicate of “ a” : 9 is 8:15. Then value of “a” is: [1 Mark, Dec. 2011]
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(c) \(\frac{4}{5} \times \sqrt{\frac{a}{9}}=\frac{8}{15}\)
or \(\frac{4}{5} \times \frac{\sqrt{a}}{3}=\frac{8}{15}\)
∴ √a = 2 ⇒ a = 4
(c) is Correct
Question 24.
If X varies inversely as square of Y and given that Y=2 for X = 1, then the value of X for Y =6 will be: [1 Mark, Dec. 2011]
(a) 3
(b) 9
(c) 1/3
(d) 6
Answer:
(d) is Correct
x × \(\frac{1}{y^2}\) ⇒ x = K.\(\frac{1}{y^2}\) x = \(\frac{k}{y^2}\), where k = proportional constant
where k = proportional constant
When x = 1 Then y = 2
1 = \(\frac{k}{2^2}\) ⇒ k = 4 ∴ x = \(\frac{4}{y^2}\)
When y = 6, Then x = \(\frac{4}{6^2}=\frac{1}{9}\)
x = \(\frac{1}{9}\)
Question 25.
Which of the numbers are not in proportion ?
(a) 6, 8, 5, 7
(b) 7, 14, 6, 12
(c) 18, 27,12, 18
(d) 8, 6, 12, 9
Answer:
(a) Go by choices
For (a) \(\frac{6}{8}=\frac{3}{4} \neq \frac{5}{7}\)
(a) is not in proportion
Question 26.
Find two numbers such that mean proportional between them is 18 and third proportional between them is 144: [1 Mark, Dec. 2012]
(a) 9 ; 36
(b) 8 ; 32
(c) 7 ; 28
(d) 6 ; 14
Answer:
(a) is correct Tricks : Go by choices
For (a) Mean Proportional of 9 and 36
= \(\sqrt{9 \times 36}\) = 18
It satisfies 1st condition.
If 144 is its 3rd condition.
362 = 9 × 144
It also satisfies the 2nd Condition.
![]()
Question 27.
Triplicate ratio of 4 : 5 is: [1 Mark, June 2013]
(a) 125 : 64
(b) 16 : 25
(c) 64 : 125
(d) 120 : 46
Answer:
(c) Triplicate ratio of 4:5 = 43 :53 = 64: 125
Question 28.
The mean proportion between 24 and 54 is _______. [1 Mark, June 2013]
(a) 33
(b) 34
(c) 35
(d) 36
Answer:
(d) Mean – Proportion = \(\sqrt{24 \times 54}\) = 36
Question 29.
The ratio of numbers is 1:2:3 and sum of their squares is 504 then the numbers are: [1 Mark, Dec. 2013]
(a) 6, 12, 18
(b) 3, 6, 9
(c) 4, 8, 12
(d) 5, 10, 15
Answer:
(a) is correct
Tricks : Go by choices
Tricks : See Quicker BMLRS
Question 30.
If P is 25% less than Q and R is 20% higher than Q the Ratio of R and P: [1 Mark, Dec. 2013]
(a) 5:8
(b) 8:5
(c) 5:3
(d) 3:5
Answer:
(b) is correct
Let Q = 100, So, P = 100 – 025 = 75
&R = 100 + 20= 120
\(\frac{R}{P}=\frac{120}{75}=\frac{8}{5}\)
Question 31.
A person has assets worth ₹ 1,48,200. He wish to divide it amongst his wife, son and daughter in the ratio 3:2:1 respectively. From this assets the share of his son will be: [1 Mark, June 2014]
(a) ₹ 74,100
(b) ₹ 37,050
(c) ₹ 49,400
(d) ₹ 24, 700
Answer:
(c) is correct
Share of son = \(\frac{2}{3+2+1}\) × 1,48,200
= ₹ 49,400
Question 32.
If x : y = 2 : 3 then (5x+2y): (3x -y) = [1 Mark, June 2014]
(a) 19 : 3
(b) 16: 3
(c) 7 : 2
(d) 7: 3
Answer:
(b) is correct
\(\frac{5 x+2 y}{3 x-y}=\frac{5 \times 2+2 \times 3}{3 \times 2-3}=\frac{16}{3}\)
Question 33.
The first, second and third month salaries of aperson are in the ratio 2:4:5. The difference between the product of the salaries of first 2 months & last 2 months is ₹ 4,80,00,000. Find the salary of the second month [1 Mark, Dec. 2014]
(a) ₹ 4,000
(b) ₹ 6,000
(c) ₹ 12,000
(d) ₹ 8,000
Answer:
(d) is correct
Let x is common in the ratio.
1st, 2nd and 3rd month salaries of a person = 2x ; 4x ; 5x
From Qts.
4x × 5x – 2x × 4x = 4,80,00,000.
or, 12x2 = 4,80,00,000.
or, x2 = 4000000
x = 2000.
2nd month salary = 4x = 4×2000
= ₹ 8000
Question 34.
(2p2 – q2) = 7pq, where p, q are positive then p : q. [1 Mark, June 2015]
(a) 5:6
(b) 5:7
(c) 3:5
(d) 3:7
Answer:
(a) is correct 15(2p2 – q2) = 7pq
Tricks : Go by choices
For (a) put p = 5; q = 6 we get
15[2 × 52 – 62] = 3 × 5 × 6
or 15 × 14 = 210
or 210 = 210
![]()
Question 35.
If one type of rice of cost ₹ 13.84 is mixed with another type of rice of cost ₹ 15.54, the mixture is sold at ₹ 17.60 with a profit of 14.6% on selling price then in which proportion the two types of rice mixed ? [1 Mark, June 2015]
(a) 3:7
(b) 5:7
(c) 7:9
(d) 9:1
Answer:
Cost of mixture per kg = 17.60 – 14.6% = 15.0304 = 15.03 (approx.)
By rules of Alligation
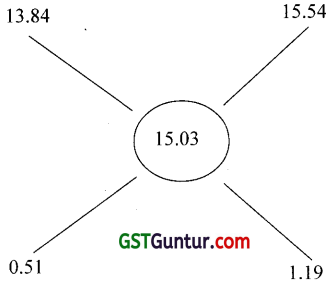
51: 119 = 3: 7
Go by choices
(a) is correct (approx)
Question 36.
Find the ratio of third proportional of 12 ; 30 and mean proportional of 9; 25 : [1 Mark, Dec. 2015]
(a) 7: 2
(b) 5 : 1
(c) 9 : 4
(d) None of these
Answer:
3rd proportional = \(\frac{30^2}{12}\) = 75
Mean Proportional = \(\sqrt{9 \times 25}\) =15
Ratio = \(\frac{75}{15}\) = 5:1
(b) is correct
Question 37.
What must be added to each of the numbers 10, 18, 22, 38 to make them proportional: [1 Mark, Dec. 2015]
(a) 5
(b) 2
(c) 3
(d) 9
Answer:
(b) is correct
let x be added.
∴ \(\frac{10+x}{18+x}=\frac{22+x}{38+x}\)
Tricks: Go by choices.
∴ x = 2 satisfies it.
Question 38.
x, y, z together starts a business, if x invests 3 times as much as y invests and y invests two third of what z invests, then the ratio of capitals of x, y, z is: [1 Mark, June 2016]
(a) 3 : 9 : 2
(b) 6: 3: 2
(c) 3 : 6 : 2
(d) 6: 2: 3
Answer:(d)
Tricks: Go by choices
6 = 3 × 2 and 2 = 3 × \(\frac{2}{3}\)
Question 39.
A bag contains 23 number of coins in the form of 1 rupee, 2 rupee and 5 rupee coins. The total sum of the coins is ?₹ 43. The ratio between 1 rupee and 2 rupees coins is 3 : 2. Then the number of 1 rupee coins is: [1 Mark, Dec. 2016]
(a) 12
(b) 8
(c) 10
(d) 16
Answer:
(a)
Tricks : Go by choices
Let option (a) is correct.
Let x is common in the ratio.
So, ₹ 1 coins = 3x = 12 ; So, x = 4
No. of ₹ 2 coins = 2 × 4 = 8
Hence no. of coins of ₹ 5 coins = 23 – 12 – 8= 3
Total money = 12 × 1 + 8 × 2 + 3 × 5 = ₹ 43
Satisfied. So (a) is correct.
Question 40.
If a: b = 2: 3, b : c = 4: 5, c: d = 6: 7 then a : d is: [1 Mark, June 2017]
(a) 24 : 35
(b) 8 : 15
(c) 16 : 35
(d) 7 : 15
Answer:
Option (c) is correct.
Multiply all ratios.
= \(\frac{2}{3} \times \frac{4}{5} \times \frac{6}{7}=\frac{16}{35}\)
Question 41.
The ratio of the number of five rupee coins to number of ten rupee coins is 8: 15. If the total value of five rupee coins is 360, then the no. of ten rupee coins is _______. [1 Mark, Dec. 2017]
Answer:
Option (d) is correct.
Total No. of ₹ 5 coins = 360/5 = 72
Let x is common in the ratio.
So, ₹ 5 coins = 8x = 72 ; So, x = 9
No. of ₹ 10 coins = 15 × 9 = 135
Question 42.
If \(\frac{1}{2}, \frac{1}{3}, \frac{1}{5}, \frac{1}{x}\) are in proportion then x = . [1 Mark, Dec. 2017]
(a) \(\frac{15}{2}\)
(b) \(\frac{3}{15}\)
(c) \(\frac{2}{15}\)
(d) \(\frac{1}{15}\)
Answer:
Option (a) is correct.
Product of middle two terms = Product of extremes
So, \(\frac{1}{2 x}=\frac{1}{15}\); x = 15/2
Question 43.
If (a + b): (b + c): (c + a) = 7 : 8 : 9 and a + b + c = 18 then a : b : c = . [1 Mark, June 2018]
(a) 5 : 4 : 3
(b) 3 : 4 : 5
(c) 4 : 3 : 5
(d) 4: 5 : 3
Answer:
(c) 4 : 3 : 5 is correct
Tricks: Go by choices.
(c) Let a : b : c = 4 : 3 : 5
It is in ratio. So, it should must satisfy given ratio (a + b): (b + c): (c + a) = 7 : 8 : 9
i.e. (4 + 3): (3 + 5): (5 + 4) = 7 : 8 : 9 (True) Avoid 2nd condition.
In detail it will take too much time.
![]()
Question 44.
If p : q is the sub-duplicate ratio of p – x2:q – x2, then x2 is : [1 Mark, May 2018]
(a) \(\frac{p}{p+q}\)
(b) \(\frac{q}{p+q}\)
(c) \(\frac{q p}{p-q}\)
(d) None
Answer:
Question 45.
The mean proportional between 24 and 54 is : [1 Mark, May 2018]
(a) 33
(b) 34
(c) 35
(d) 36
Solution:
Formula
Mean Proportion of a & b = \(\sqrt{a b}\)
(d) = \(\sqrt{24 \times 54}\) = 36
Question 46.
\(\frac{3 x-2}{5 x+6}\) is the duplicate ratio of \(\frac{2}{3}\) then find the value of x : [1 Mark, Nov. 2018]
(a) 6
(b) 2
(c) 5
(d) 9
Answer:
(a)
Given \(\frac{3 x-2}{5 x+6}=\left(\frac{2}{3}\right)^2=\frac{4}{9}\)
Tricks : Go by choices
for option (a) putting x = 6 in LHS; we get
\(\frac{3 \times 2-2}{5 \times 2+6}=\frac{4}{9}\)
∴ (a) is correct.
Question 47.
If x : y : z = 7 : 4 : 11 then is: [1 Mark, Nov. 2018]
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(a)
\(\frac{x+y+z}{z}=\frac{7+4+11}{11}\) = 2
Question 48.
If the ratio of two numbers is 7 : 11. If 7 is added to each number then the new ratio will be 2 : 3 then the numbers are. [1 Mark, June 2019 ]
(a) 49,77
(b) 42,45
(c) 43,42
(d) 39,40
Answer:
Tricks:- GBC (Go by Choices)
(a)
49 ÷ 7 = 7
77 ÷ 11 = 7 both must be equal.
Here it is correct.
Now:
\(\frac{49+7}{77+7}=\frac{56}{84}=\frac{2}{3}\)
Divide 56 by numerator (2) and 84 by Denominator (3) we get same value “28”
Note:- No need to solve ; only check.
By Calculator.