Quadratic Equations – CA Foundation Maths Study Material

This Quadratic Equations – CA Foundation Maths Study Material is designed strictly as per the latest syllabus and exam pattern.

Quadratic Equations – CA Foundation Maths Study Material

ax² + bx + c = 0; where a ≠ 0; a,b,c, are constants form equation is called Quadratic Equation or Second degree equation.
I. If b = 0 Then ax² +c = 0 is called PURE Quadratic Equation.
II. If b ≠ 0 Then the equation, ax² + bx + c = 0 where a ≠ 0 is called an AFFECTED Quadratic Equation.

Roots:
The value of the variable “x” which satisfies the given equation is called its Solution or roots of the Quadratic Equation.
Discriminant
For Quad. Eqn. ax² + bx + c = 0.
Discriminant D = b² – 4ac.
Example
For Eqn. 3x² + 7x + 2 = 0.
a = 3;b = 7;c = 2 Discriminant D = b² – 4a c
= 7² – 4.3.2 = 49 – 24 = 25.

III. Roots of Quad. Eqn. ax² + bx + c = 0 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}=\frac{-b \pm \sqrt{D}}{2 a}\)
[Remember this formula, No need to prove it.]

IV. If a and f are roots of a Quadratic Equation ax² + bx + c = 0
Then α + β = \(\frac{-b}{a}\)
∴ Sum of roots = \(\)
αβ = \(\frac{c}{a}\)

V. If α and β are roots of a Quadratic Eqn. Then the eqn. is
x² – (α + β)x+a P =0
⇒ x² – (sum of roots) x + Product of roots = 0.

VI. Nature of Roots
Nature of roots of a Quad. Eqn. depends upon Discriminant D = b² – 4ac.
(A) If D > 0, Roots Real & Unequal
(i) D a perfect square then roots are Rational & unequal
As. \(\frac{2}{3} ;-\frac{2}{3}\)
(ii) D not a perfect Square.
Then roots are irrational & unequal and Conjugated As. 2 + √3; √5
(B ) If D = 0, Then Roots are Real & equal. b
Each root = –\(-\frac{b}{2 a}\)
(C) If D < 0, Then Roots are imaginary.

VII. If one root of a quadratic Eqn. is irrational then its other root is its irrational conjugate.
Example
If one root = 3+ √5
Then other root = 3 – √5 (irrational conjugate)
[To find conjugate change the sign of irrational part.]
Note:
(i) If one root is reciprocal to the other Then c = a
(ii) If one root is equal to the other but opposite in sign. Then b = 0.

Cubic Equations
1. Meaning of Cubic Equation The equation having form. ax³ + bx² + cx + d = 0, a 0,
Where a, b, c, d are real numbers , is called a cubic equation.

2. Relation Between Roots and Coefficients
If α, β, γ are the roots of the cubic equation ax³ + bx³ + cx + d = 0, a ≠ 0, then
(i) α + β + γ = \(\frac{-b}{a}\)
(ii) αβ + βγ + γα = \(\frac{c}{a}\)
(Hi) αβγ = \(\frac{-d}{a}\)

3. The Cubic equation having roots a, p, y is
x³ – (α + β + γ)x² + (αβ + βγ + γα)x – αβγ = 0

Previous Year Exam Questions

Question 1.
On Solving \(\sqrt{\frac{x}{1-x}}+\sqrt{\frac{1-x}{x}}\) = 2\(\frac{1}{6}\), we get one value of x as:
(a) \(\frac{4}{13}\)
(b) \(\frac{1}{13}\)
(c) \(\frac{2}{13}\)
(d) \(\frac{3}{13}\)
Answer:
\(\sqrt{\frac{x}{1-x}}+\sqrt{\frac{1-x}{x}}=\frac{13}{6}\)
Tricks : RHS is in fraction (i.e. rational No.)
Numerator value of x and 1-x must be a perfect square.
∴ (a) \(\frac{4}{13}\) = x must be its answer.

(a) is correct
Detail Method It is too much time taking.

Question 2.
Find the positive value of k for which the equations : x² + kx + 64 = 0 and x² – 8x + k = 0 will have real roots:
(a) 12
(b) 16
(c) 18
(d) 22
Answer:
(b) For Real roots
D = b² -4ac ≥ 0
or b² ≥ 4ac
For eqn(1); k² ≥ 4.1.64 ⇒ k ≥ 16 ……….(I)
For eqn (2) (-8)² ≥ 4.1.k ⇒ k ≤ 16 ……….(II)
Clearly k = 16 satisfies (I) & (II)
∴ (b) is correct.

Question 3.
If one root of an equation is 2 + √5, then the quadratic equation is:
(a) x² + 4x – 1 = 0
(b) x² – 4 x – 1 = 0
(c) x² + 4x + 1 = 0
(d) x² – 4x + 1 = 0
Answer:
(b) If one root = 2 + √5
Its other root = 2 – √5 (Irrational conjugate) Eqn is
x² – (Sum of roots) x + Product of roots = 0
or x² – (2 + √5 + 2 – √5)x + (2 + √5)(2 – √5)=0
or x² – 4x + (4 – 5) = 0
or x² – 4x – 1 = 0
(b) is correct.

Question 4.
A man starts his job with a certain monthly salary and earns a fixed increment every year. Ifhis salary was ₹ 1,500 after 4 years of service and ₹ 1,800 after 10 years of service, what was his starting salary and what is the annual increment in rupees? [1 Mark, May 2007]
(a) ₹ 1,300, ₹ 50
(b) ₹ 1,100, ₹ 50
(c) ₹ 1,500, ₹ 30
(d) None
Answer:
(a) Tricks : Go by choices.
For (a) Salary After 4 yrs 1300 + 4x 50 = ₹ 1500
Salary after 10 yrs = 1300 + 10x 50 = ₹ 1800
∴ (a) is correct Detail Method
Let Fixed Salary = a
Increment per yr = b
Salary after t yrs = s
s = a + bt
∴ a + b × 4 = 1500 = a + 4b = 1500 (1)
a + b × 10 = 1800 = a+ 10b = 1800 (2)
Eqn. (2) – Eqn. (1); we get
a + 10b = 1800
a + 4b = 1500
6b = 300 ∵ b = \(\frac{300}{6}\) = ₹ 50 o
From (1) a + 4 × 50 = 1500
or a = 1500 – 200 = ₹ 1300
(a) is correct

Question 5.
The sides of an equilateral triangle are shortened by 12 units, 13 units and 14 units respectively and a right angled triangle is formed. The side of the equilateral triangle is : [1 Mark, May 2007]
(a) 17 units
(b) 16 units
(c) 15 units
(d) 18 units
Answer:
Tricks : Go by choices
For (a) let each side =17 units.
∴ Sides are 17 -12 ; 17 -13
and 17 -14 = 5 ; 4 and 3 units respectively
They make a right angled triangle because sum of squares of two sides is equal to square of Largest side.
(a) is Correct

Detail Method
Let length of each side = x
Side of the right angle triangle are x – 12; x – 13 and x – 14
∴ By Pythagoras Theorem (x – 12)² = (x – 13)² +(x – 14)²
or x² – 24x + 144 = x² – 26x + 169 + x² – 28x + 196
or 0 = x² – 30x + 221
or x² – 17x – 13x + 221 = 0
or x(x – 17) – 13(x – 17) = 0
or (x – 17)(x – 13) = 0
x = 17 ; 13
No side = x – 13 =0 x=17
∴ (a) is correct.

Question 6.
The value of \(\sqrt{6+\sqrt{6+\sqrt{6+\ldots \ldots \ldots \infty}}}\) is:
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
Tricks :
(c) \(\sqrt{6+\sqrt{6+\sqrt{6+\ldots \ldots \ldots \infty}}}\) = +3
Find two factors of 6 such that their difference becomes 1.
6 = 3 × 2
(i) Give + sign for = Greater factor
(ii) – sign for Smaller factor
(c) is Correct

Question 7.
Area of a rectangular garden is 8000 square metres. Ratio in length and breadth is 5:4. A path of uniform width, runs all round the inside of the garden. If the path occupies 3200 m², what is its width? [1 Mark, Nov. 2007]
(a) 12m
(b) 6m
(c) 10m
(d) 4m
Answer:
(c) Let x is common in the ratio
∴ length = 5x and Breadth = 4x
∴ Area = 5x × 4x = 8000
or 20x² = 8000
or x² =400 = 20²
x = 20
Length = 5x = 5 × 20 = 100m
Breadth = 4x = 4 × 20 = 80 m
Let Width of Path = ym
∴ Area of rest part = 8000 – 3200
or (100 – 2y) (80 – 2y) = 4800
Tricks : Go by choices.
(c) y = 10 m Satisfies it
Width = 10m is correct

Question 8.
The value of: [1 Mark, June 2008]

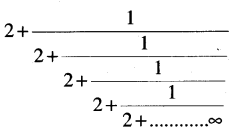
(a) 1 ± √2
(b) 2 + √5
(c) 2 ± √3
(d) None
Answer:
(a) let x =

(a) is correct

Question 9.
If x³ – 6x² + 11x -6 = 0 then find the value of (3x – 4). [1 Mark, Dec. 2008]
(a) (1, 2, 3)
(b) (-1, 2, 5)
(c) (-1, 3, 5)
(d) (2, 3, 5)
Answer:
(a) Tricks : Go by choices For(a)
Let, 3x – 4 = -1 ; 3x = 3 ; So, x = 1
Putting x = 1 in the given eqn ; we get
LHS = 13 – 6 × 12 + 11 × 1 – 6 = 0 = RHS
Similarly, 3x – 4 =2 ; So x = 2
For x = 2 ; LHS = 23 – 6 × 22 + 11 × 2 – 6
= 8 – 24 + 22 – 6 = 0 = RHS
Similarly, 3x – 4 = 5; So x = 3
For x = 3;
LHS = 33 – 6 × 32 +11 × 3 – 6
= 27 – 54 + 33 – 6 = 0 = RHS
∴ (a) is correct

Question 10.
If (2 + √3 ) is a root of a quadratic equation x² + px + q = 0 then find the value of p and Question
Answer:
Tricks:
One root = 2 + √3
∴ Another root =2-73
∴ Eqn is
x² – (2 + √3 + 2 – √3)x + (2 + √3)(2 – √3) = 0
or x² – 4x + (4 – 3) = 0
Comparing it with x² + px + q = 0
p = -4 & q = 1
∴ (c) is correct

Question 11.
If area and perimeter of a rectangle is 6000 cm2 and 340 cm respectively, then the length of rectangle is : [1 Mark, Dec. 2008]
(a) 140
(b) 120
(c) 170
(d) 200
Answer:
(b) Let length = 1 & Breadth = b
lb = 6000 ………(1)
2(l + b) = 340
or l + b = 170 …………(2)
Tricks:
Then Go by choices
For (a) if l = 140 Then b = 170 – 140 = 30
∴ lb = 140 × 30 = 4200 ≠ 6000
∴ (a) is not the answer
For (b) if 1 = 120
Then 120+ b= 170
∴ b = 170 – 120 = 50
∴ Area = lb = 120x 50 = 6000
∴ (b) is correct

Question 12.
A straight line passes through the point (3,2). Find the equation of the straight line. [1 Mark, June 2009]
(a) x + y = 1
(b) x + y = 3
(c) x + y = 5
(d) x + y = 2
Answer:
(c) It cannot be solved properly because only one condition is given For Answer.
Tricks: Go by choices
(c) Point (3 ; 2) satisfies x + y = 5
∴ (c) is correct

Question 13.
One root of the equation: x² – 2(5 + m) + 3(7 + m) = 0 is reciprocal of the other. [1 Mark, June 2009]
Find the value of m.
(a) -20/3
(b) 7
(c) 1/7
(d) 117
Answer:
(a)
Let one root = α, Then other root = \(\frac{1}{α}\)
α × \(\frac{1}{\alpha}=\frac{3(7+\mathrm{m})}{1}\)
1 = 21 + 3m
or 3m = -20 m = \(\frac{-20}{3}\)
(a) is correct

Question 14.
Roots of the equation 3x² – 14x – k = 0 will be reciprocal of each other if: [1 Mark, June 2010]
(a) k= -3
(b) k = 0
(c) k = 3
(d) k = 14
Answer:
(c) is correct.
Let one root = α & Another root = \(\frac{1}{α}\) (given)
∵ Product of roots = c/a
α.\(\frac{1}{α}\) = — a 3
∴ 1 = \(\frac{k}{3}\) So, K = 3
∴ (c) is correct

Question 15.
Positive value of‘k’ for which the roots at equation 12x² + kx + 5 = 0 are in ratio 3 :2, is: [1 Mark, Dec. 2010]
(a) 5/12
(b) 12/5
(c) \(\frac{5 \sqrt{10}}{2}\)
(d) 5\(\sqrt{10}\)
Answer:
Let a is common in the ratio.
∴ Roots are 3α and 2α
Sum of roots = \(-\frac{b}{a}\)
∴ 3α + 2α = 5α = \(-\frac{k}{12}\)
So, α = \(-\frac{k}{60}\)
Product of roots = 3α × 2α = \(\frac{c}{a}\)
∴ 6α² = \(\frac{5}{12}\)
⇒ 6.\(\left(-\frac{k}{60}\right)^2=\frac{5}{12}\), So, k² = 250
k = 5\(\sqrt{10}\)
∴ (d) is correct

Question 16.
If one root of the equation x² – 3x + k = 0 is 2, then value of k will be : [1 Mark, Dec. 2010]
(a) -10
(b) 0
(c) 2
(d) 10
Answer:
(c) is correct
2 is a root of given eqn.
∴ 2² – 3 × 2 + k = 0
or -1 + k = 0
∴ k = 2
∴ (c) is correct

Question 17.
It roots of equation x² + x + r = 0 are ‘α’ and ‘β’ and α³ + β³ = -6 . Find the value of ‘r’? [1 Mark, June 2011]
(a) \(\frac{-5}{3}\)
(b) \(\frac{7}{3}\)
(c) \(\frac{-4}{3}\)
(d) 1
Answer:
(a) is correct.
α + β = \(\frac{-1}{1}\) = -1 & = αβ = r
∴ α³ + β³ = -6
or (α + β)³ – 3αβ(α + β) = -6
or (-1)³ – 3r(-1) = -6
or -1 + 3r = -6;
or 3r = -5
r = -5/3
∴ (a) is correct

Question 18.
If one root of the Equation px² + qx + r = 0 is r then other root of the Equation will be: [1 Mark, Dec. 2011]
(a) 1/q
(b) 1/r
(c) 1/p
(d) \(\frac{1}{p+q}\)
Answer:
(c) Let α is another root.
rα = \(\frac{r}{p}\)
∴ α = \(\frac{1}{p}\)

Question 19.
If the ratio of the root of the Equation 4x² – 6x + p = 0 is 1:2 then the value of p is: [1 Mark, Dec. 2011]
(a) 1
(b) 2
(c) -2
(d) -1
Answer:
(b) Let a is common in the ratio
∴ α + 2α = \(\frac{-(-6)}{4}\) ⇒ α = \(\frac{1}{2}\)
∴ α.2α = \(\frac{p}{4}\)
∴ p = 8α² = 8.\(\frac{1}{4}\) = 2

Question 20.
If p & q are the root of the Equation x² – bx + c =0, then what is the Equation whose roots are (pq + p + q) and (pq – p – q) ? [1 Mark, Dec. 2011]
Answer:
(a) Eqn is x² – (p + q)x + pq = 0
∴ b = p + q ; C = pq
New roots are pq + (p + q) = c + b
& pq – (p + q) = c – b
∴ Eqn is
x² – (c + b + c – b)x + (c + b)(c – b) = 0
or x² – 2cx + c² – b² = 0

Question 21.
If arithmetic mean between roots of a quadratic equation is 8 and the geometric mean between them is 5, the equation is: [1 Mark, June 2012]
O) x² – 16x – 25 = 0
(b) x² – 16x + 25 = 0
(c) x² – 16x + 5 = 0
(d) None of these
Answer:
(b) Let α and β are two roots.
(α + β)/2 = 8 and \(\sqrt{αβ}\) = 5
⇒ α + β =16 & αβ = 25
Eqn. is x² – 16x + 25 = 0

Question 22.
The minimum value of the function x² – 6x +10 is
(a) 1
(b) 2
(c) 3
(d) 10
Answer:
(a) coeff. of x² = 1 > o; function is minimum (Formula) i
Minimum value = \(\frac{4 a c-b^2}{4 a}\)
\(\frac{4.1 .10-(-b)^2}{4 \times 1}=\frac{4}{4}\) = 1

Question 23.
Ifoneofthe roots of the equation x² + px + a is √3 + 2, then the value of ‘p’ and ‘a’ is: [1 Mark, June 2012]
(a) -4, -1
(b) 4, -1
(c) -4, 1
(d) 4, 1
Answer:
(c) Roots are 2 + √3 and 2 – √3 (conjugate of 2 + √3)
Eqn is
x² – (Sum of roots) x + product of roots = 0
x² – 4x + (4 – 3) = 0
x² + px + a = 0
∴ P = -4 ; a = 1

Question 24.
Roots of equation 2x² + 3x + 7 = 0 are α and p. The value of αβ^-1 + βα^-1 is: [1 Mark, Dec. 2012]
(a) 2
(b) 3/7
(c) 7/2
(d) -19/14
Answer:

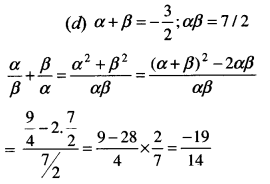
Question 25.
The quadratic equation x² – 2kx + 16 = 0 will have equal roots when the value of ‘k’ is: [1 Mark, Dec. 2012]
(a) ±1
(b) ±2
(c) ±3
(d) ±4
Answer:
(d) Let roots are α; α
∴ α + α = \(\frac{-(-2 k)}{1}\) ⇒ α = k
α.α = k.k = 16 ⇒ k² = 16 ⇒ k = ±4

Question 26.
If α, β are roots of x² + 7x + 11 = 0 then the equation whose roots as (α + β)² &.(α – β)² is: [1 Mark, June 2013]
(a) x² – 54x + 245 = 0
(b) x² – 14x + 49 =0
(c) x² – 24x + 144 = 0
(d) x² – 50x + 49 = 0
Answer:
(a) is correct
α + β = \(-\frac{b}{a}=-\frac{7}{1}=\) = -7
αβ = \(\frac{c}{a}=\frac{11}{1}\) = 11
(α – β)² -(α + β)² – 4αβ
= (-7)² – 4 × 11 = 5

Required eqn. is
x² – {(α + β)² + (α – β)²}x + (α + β)²(α – β)² =0
or x² – (49+5)x + 49 × 5 = 0
or x² – 5x + 245 = 0
∴ (a) is correct

Question 27.
If b² – 4ac is perfect square but not equal to zero then the roots of the equation ax² + bx + c = 0 are: [1 Mark, Dec. 2013]
(a) Real and equal
(b) Real irrational and equal
(c) Real rational and unequal
(d) Imaginary
Answer:
(c) b² -4ac > 0 & perfect square Roots are real rational and unequal

Question 28.
Divide 80 into two parts so that their products is maximum then the numbers are: [1 Mark, Dec. 2013]
(a) 15, 65
(b) 25, 55
(c) 35, 45
(d) 40, 40
Answer:
(d) is correct
Let 1st part = x
∴ 2nd part 80 -x
Let y = x(80 – x) = -x² + 80x
Here co. eff. of x² < 0
y is maximum at
x = \(\frac{-b}{2 a}=-\frac{80}{2(-1)}\) = 40
∴ Numbers are (40 ; 40)
Tricks : Go by choices.

Question 29.
The roots of equation y³ + y² – y – 1 = 0 are
(a) 1,1,-1
(b) -1,-1,1
(c) 1,1,1
Answer:
(b) is correct
y³ + y² – y – 1 = 0
or y²(y + 1) – 1(y + 1) = 0
or (y + 1)(y² – 1) = 0
or(y + 1)(y + 1)(y – 1)=0
y = -1 ; -1; 1.
Tricks : Go by choices.

Question 30.
If α, β are the roots of the quadratic equation 2x² – 4x = 1 then the value \(\frac{\alpha^2}{\beta}+\frac{\beta^2}{\alpha}\) =
(a) -11
(6) 22
(c) -22
(d) 11
Answer:
2x² – 4x – 1 = 0
Let α and β are its roots

Question 31.
If α, β be the roots of a quadratic equation if α + β = -2, αβ = -3 Find quadratic equation: [1 Mark, Dec. 2015]
(a) x² + 2x – 7 = 0
(c) x² + 2x – 3 = 0
(c) x² – 2x – 3 = 0
(d) x² – 2x + 7 = 0
Answer:
(b) is correct Quadratic Eqn. is
x² – (α + β)x + αβ = 0
x² – (-2)x + (-3) = 0
∴ x² + 2x – 3 = 0

Question 32.
Value of k for which roots are equal of given equation 4x² – 12x + k = 0. [1 Mark, Dec. 2015]
(a) 144
(6) 9
(c) 5
(d) None of these
Answer:
(b) is correct 4x² – 12x + k = 0
D = b² – 4.ac = 0
= (-12)² = 4 × 41
Or, 144 = 16k ∴ k =9

Question 33.
If difference between the roots ofthe equation x² – kx + 8 = o is 4 then the value of K is: [1 Mark, June 2016]
(a) 0
(b) ±4
(c) ±8√3
(d) ±4√3
Answer:
(d) is correct.
let α, β are roots of x² – kx + 8 = 0
∴ α + β = -b/a = \(-\frac{(-k)}{1}\) = k & α. β = c/a = 8/1 = 8
(α – β)² = (α + β)² – 4αβ = 4²
⇒ k² – 4 × 8 = 16
or k² = 48 ⇒ k = ±\(\sqrt{16 \times 3}\) ⇒ k = ±4√3
(d) is correct.

Question 34.
If α, β be the roots of x² + x + 5 = 0 then \(\frac{\alpha^2}{\beta}+\frac{\beta^2}{\alpha}\) = ___. [1 Mark, June 2017]
(a) \(\frac{16}{5}\)
(b) 2
(c) 3
(d) \(\frac{14}{5}\)
Answer:

(d) is correct.

Question 35.
If the sum of two numbers is 13 and the sum of their squares is 85 then the numbers are : [1 Mark, Dec. 2017]
(a) 6, 7
(b) 4, 9
(c) 10, 3
(d) 5, 8
Answer:
(a)
Tricks : GBC (Go by choices)
6 +7 = 13 (True)
& 6² + 7² = 36 + 49 = 85 (True)

Question 36.
The difference between the roots of the equation x² – 7x – 9 = 0 is : [1 Mark, Dec. 2017]
(a) 7
(b) \(\sqrt{85}\)
(c) 9
(d) 2\(\sqrt{85}\)
Answer:
(b)
Let α and J3 are roots.
α + β = \(-\frac{b}{a}=-\frac{-7}{1}\) = 7
αβ = \(\frac{c}{a}=\frac{-9}{1}\) = -9.
∴ (α – β)² = (α + β)² – 4
αβ = 7² – 4(-9) = 85
α.β = \(\sqrt{85}\)

Question 37.
The roots of the cubic equation x³ + 7x² – 21x – 27 = 0 is ___ : [1 Mark, Dec. 2017]
(a) -1, 3, 9
(6) 1, -3, 9
(c) -1, 3, -9
(d) -1, -3, 9
Answer:
(c)
TRICKS: – Go by choices.

Question 38.
If the roots of the equation kx² – 3x -1= 0 are the reciprocal of the roots of the equation x² + 3x – 4 = 0 then K =
(a) 4
(b) -4
(c) 3
(d) -3
Answer:
(a)
∵ x² + 3x – 4 = 0
or; x² – 4x + x – 4 = 0
or; x(x – 4) + 1(x – 4) = 0
or; (x – 4)(x + 1) = 0
x = 4; -1
Eqn. having roots \(\frac{1}{2}\) & \(\frac{1}{-1}\) = \(\frac{1}{4}\) & – 1 is.
or x² – (\(\frac{1}{4}\) – 1) + \(\frac{1}{4}\)(-1) = 0
or x² + \(\frac{3}{4}\)x – \(\frac{1}{4}\) = 0
Multiplying by 4 ; we get
4x² + 3x -1 = 0
Comparing it with kx² + 3x -1 = 0
We get K = 4
Tricks : Eqn. having roots the reciprocal of the roots of ax² + bx + c = 0 is cx² + bx +a = 0 i.e. 1st and last term interchanges.

Question 39.
If the roots of the equation x² – 15x² + kx – 45 = 0 are in A.P., find value of k: [1 Mark, June 2018]
(a) 56
(b) 59
(c) -56
(d) -59
Answer:
∵ Roots are in A.R
Let roots are a – d; a; a + d
So, (a – d)+a + (a + d) = 15
or; 3a = 15
or; a = 5
And Product of roots
(a – d ). a . (a + d ) = 45
or (5 – d);5. (5 + d) = 45
or 25 – d² = 9
or; d² = 25 – 9 = 16
or; d = \(\sqrt{16}\) = 4
Hence; roots are
a – d, a, a + d = 5 – 4; 5; 5 + 4
= 1; 5 ; 9.
The value of K
= Sum of product of two roots in a order
= (1 × 5) + (5 × 9) + (9 × 1)
= 5 + 45 + 9 = 59
(b) is correct.

Tricks : If α; β and γ are the roots of a cubic Eqn.
So ; Cubic Eqn. is
x³ – (α + β + γ)x² + (αβ + βγ + γα)x – αβγ = 0
Given Eqn. is
x³ – 15x² + k . x – 45 = 0
Comparing it,
α + β + γ = 15 ⇒ 1 + 5 + 9 = 15
& αβγ = 45 ⇒ 1 × 5 × 9 = 45
[Apply Hit and Trial method which can satisfy both]
Hence ; we can say ;
α = 1; β = 5; γ = 9;
k = αβ + βγ + γα= 1 × 5 + 5 × 9 + 9 × 1 = 59

Question 40.
If α + β = -2 and αβ = -3 where a and are the roots of the equation, which is [1 Mark, May 2018]
(a) x² – 2x – 3 = 0
(b) x² + 2x – 3 = 0
(c) x² + 2x + 3 = 0
(d) x² – 2x + 3 = 0
Answer:
(b)
Quadratic Eqn. having roots α and β is
x² – (α + β)x + αβ = 0
or ; x² – (- 2)x + (- 3)= 0
or; x² + 2x – 3 = 0
(b) is correct.

Question 41.
If α and β are the roots of the equation x² + x + 5 = 0 equal to: [1 Mark, May 2018]
(a) \(\frac{16}{5}\)
(b) 3
(c) 7
(d) 2
Answer:
(c)
Given Eqn. is x² + x + 5 = 0.

(c) is correct.

Question 42.
When two roots of quadratic equation are α, \(\frac{1}{α}\) then what will be the quadratic equation: [1 Mark, Nov. 2018]
(a) αx² – (α² + 1)x + a = 0
(b) αx² – αx² + 1 = 0
(c) αx² – (α² + 1)x + 1 = 0
(d) None of these
Answer:
(a)
Tricks : For (a) α. \(\frac{1}{α}\) = 1 = \(\frac{c}{a}=\frac{\alpha}{\alpha}\) = 1 (True)

Question 43.
Let α and β be the roots of x² + 7x + 12 = 0 Then the value of \(\left(\frac{\alpha^2}{\beta}+\frac{\beta^2}{\alpha}\right)\) will be: [1 Mark, Nov. 2018]
(a) \(\frac{49}{144}+\frac{144}{49}\)
(b) \(\frac{7}{12}+\frac{12}{7}\)
(c) \(-\frac{91}{12}\)
(d) None of these
Answer:
(c)
x² + 7x + 12 = 0
or x² + 4x +3.x+ 12 = 0
or x(x + 4)+3(x + 4) = 0
or (x + 4) (x + 3) = 0
x = – 3, 4
let α = -3; β = -4

Question 44.
Find the condition that one root is double the of ax² + bx + c = 0 [1 Mark, June 2019]
(a) 2b² = 3ac
(b) b² = 3ac
(c) 2b² = 9ac
(d) None
Answer:
(c)
Tricks
Let 1st root = 1
Then 2nd root = 2
The Eqn. is x² – (1 + 2) + 1 × 2 = 0
or x² – 3x + 2 = 0
Comparing it with ax² + bx + c = 0 we get;
a = 1; b = -3 ; c = 2
Go by choices (GBC)
(a) 2b² = 3ac
2.(-3)² =3.1.2 (False)
(c) 2b² =9.ac
2. (-3)² = 9.1.2
⇒ 18 = 18 (True)
Hence, Option (c) is (true)