Portfolio Management – CA Final SFM Study Material is designed strictly as per the latest syllabus and exam pattern.
Portfolio Management – CA Final SFM Study Material
Part – 1 (Theory)
Question 1.
Discuss the various kinds of Systematic and Unsystematic risk? [Practice Question]
Answer:
There are two types of risk – systematic (or non-diversifiable) and un-systematic (or diversifiable) relevant for investment – also, called as general and specific risk.
Types of Systematic Risk:
i. Market risk: Even if the earning power of the corporate sector and the interest rate structure remain more or less unchanged, prices of securi-ties, equity shares in particular, tend to fluctuate. Major cause appears to be changing psychology of the investors. The irrationality in the security markets may cause losses unrelated to the basic risks. These losses are the result of changes in the general tenor of the market and are called market risks.
ii. Interest Rate Risk: The change in the interest rate has a bearing on the welfare of the investors. As the interest rate goes up, the market price of existing fixed income securities falls and vice versa. This happens because the buyer of a fixed income security would not buy it at its face value if its interest rate is lower than the prevailing interest rate on a similar security.
iii. Social or Regulatory Risk: The social or regulatory risk arises, where an otherwise profitable investment is impaired as a result of adverse legislation, harsh regulatory climate, or in extreme instance nationalization by a socialistic government.
iv. Purchasing Power Risk: Inflation or rise in prices lead to rise in costs of production, lower margins, wage rises and profit squeezing etc. The return expected by investors will change due to change in real value of returns.
Types of Unsystematic Risk:
i. Business Risk: As a holder of corporate securities (equity shares or debentures) one is exposed to the risk of poor business performance. This ” may be caused by a variety of factors like heightened competition, emergence of new technologies, development of substitute products, shifts in consumer preferences, inadequate supply of essential inputs, changes in government policies etc. But quite often the principal factor may be inept and incompetent management.
ii. Financial Risk: This relates to the method of financing, adopted by the company, high leverage leading to larger debt servicing problem or short term liquidity problems due to bad debts, delayed receivables and fall in current assets or rise in current liabilities.
iii. Default Risk: Default risk refer to the risk accruing from the fact that a borrower may not pay interest and/or principal on time. Except in the
Question 2.
Discuss the capital Asset pricing Model (CAPM) and its relevant assumptions [May 2018] [5 marks]
Answer:
Capital Asset Pricing Model: The mechanical complexity of the Markowitz’s Portfolio model kept both practitioners and academics away from adopting the concept for practical use. Its intuitive logic, however, spurred the creativity of a number of researchers who began examining the stock market implications that would arise if all investors used this model. As a result what is referred to as the Capital Asset Pricing Model (CAPM), was developed.
The capital Asset pricing model was developed by Sharpe, Mossin and Lintner in 1960. The model explains the relationship between the expected return, non-diversifiable risk and the valuation of securities. It considers the required rate of return of a security on the basis of its contribution to total risk. It is based on the premise that the diversifiable risk of a security is eliminated when more and more securities are added to the portfolio. However, the systematic risk cannot be diversified and is or related with that of the market portfolio. As per CAPM,
Expected return on security = Rf + Beta (Rm – Rf).
Assumptions of CAPM:
- The investor’s objective is to maximize the utility of terminal wealth.
- Investors make choices on the basis of risk and return.
- Investors have identical time horizon.
- Investors have homogenous expectations of risk and return.
- Information is simultaneously and freely available to all investors.
- There are no taxes, transaction costs, restrictions on short sales or other market imperfections.
- Total asset quality is fixed and all assets are marketable and divisible.
![]()
Question 3.
Explain the three form of Efficient Market Hypothesis. [Practice Question]
Answer:
The Efficient Market Hypothesis (EMH) is concerned with speed with which information affects the prices of securities. As per the study carried out by the technical analysts, it was observed that information is slowly incorporated in the price and it provides an opportunity to earn excess profit. However, once the information is incorporated then investor can not earn this excess profit.
Level of Market Efficiency: If price reflects all information, it is the highest order of market efficiency.
According to FAMA, there exist three levels of market efficiency:-
- Weak form efficiency – Price reflect all information found in the record of past prices and volumes.
- Semi – strong efficiency – price reflect not only all information found in . the record of past prices and volumes but also all other publicly available information.
- Strong form efficiency – price reflect all available information public as well as private.
Question 4.
Explain the different challenges to Efficient Market Theory. [Practice Question]
Answer:
Some of the major challenges to efficient market theory are:
a. Information Inadequacy: Information is neither freely available nor rapidly transmitted to all participants in the stock market. There is a calculated attempt by many companies to circulate misinformation.
b. Limited information processing capabilities: Human information processing capabilities are sharply limited. According to Herbert Simon every human organism lives in an environment which generates millions of new bits of information every second but the bottle necks of the perceptual apparatus does not admit more than thousand bits per second and possibly much less.
David Dreman maintained that under conditions of anxiety and uncertainty, with a vast interacting information grid, the market can become a giant.
c. Irrational Behaviour – It is generally believed that investors’ rationality will ensure a close correspondence between market prices and intrinsic values. But in practice this is not true. J. M. Keynes argued that all sorts of consideration enter into the market valuation which is in no way relevant to the prospective yield. This was confirmed by L.C. Gupta who found that the market evaluation processes work haphazardly almost like a blind man firing a gun. The market seems to function largely on hit or miss tactics, rather than on the basis of informed beliefs about the long Term prospects of individual enterprise.
d. Monopolistic Influence – A market is regarded as highly competitive. No single buyer or seller is supposed to have undue influence over prices but in practice, powerful institutions and big operators wield great influence over the market. The monopolistic power enjoyed by them diminishes the competitiveness of the market.
Part – 2 (Numerical Problems: Topic)
Question 1.
Amal Ltd. has been maintaining a growth rate of 12% in dividends. The company has paid dividend @ Rs. 3 per share. The rate of return on market portfolio is 15% and the risk-free rate of return in the market has been observed as 10%. The beta co-efficient of the company’s share is 1.2.
You are required to calculate the expected rate of return on the company’s shares as per CAPM model and the equilibrium price per share by dividend growth model. [Nov. 2010] [5 Marks]
Answer:
Capital Asset Pricing Model (CAPM) formula for calculation of expected rate of return is
ER = Rf + β(Rm – Rf)
Where,
ER = Expected Return
β = Beta of Security
Rm = Market Return
Rf = Risk free Rate
= 10 + [1.2 (15 – 10)]
= 10 + 6 = 16%
As per dividend Price model with constant growth, the equilibrium price:-
Where,
Ke = \(\frac{D_1}{P_0}\) + g
Ke = Expected Return
D1 = Dividend expected after 1 year
P0 = \(\frac{D_1}{K e-g}\)
P0 = Market Price of the share
g = Growth rate
P0 = \(\frac{3(1.12)}{0.16-0.12}\)
P0 = \(\frac{3.36}{0.04}\) = Rs, 84
Therefore, equilibrium price per share will be Rs. 84.
Question 2.
A holds the following portfolio:
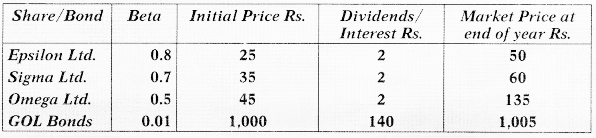
Calculate:
(i) The expected rate of return on his portfolio using Capital Asset Pricing Method (CAPM) ‘
(ii) The average return of his portfolio.
The Risk-free return is 14%. [May 2008] [10 Marks]
Answer:
(i) Expected rate of return
Expected Return on market portfolio
= \(\frac{\text { Dividend }+ \text { Capital Gains }}{\text { Initial investment }}=\frac{146+145}{1105}\) = 26.33%
Return as per CAPM
ERp = RF + β (RM – RF)
| Gold Ltd. | 14+ 0.6 [16.84- 14] | = 14+1.70 | = 15.70% |
| Silver Ltd. | 14+ 0.8 [16.84- 14] | = 14 + 2.27 | = 16.27% |
| Bronze Ltd. | 14 +0.6 [ 16.84- 14] | = 14+1.70 | = 15.70% |
| GOI Bonds | 14+1.0 [16.84- 14] | = 14 + 2.84 | = 16.84 |
(ii) Average Return of Portfolio (Based on simple average.)
\(\frac{23.86+22.63+20.17+14.12}{4}=\frac{80.78}{4}\) = 20.20%
Alternatively, first simple average of the Beta can be calculated and then the CAPM applied:
= \(\frac{0.8+0.7+0.5+0.01}{4}=\frac{2.01}{4}\) = 0.5025
14 + 0.5025 (26.33 – 14)
14 + 6.20 = 20.20%
Question 3.
Mr. Fed Up wants to invest an amount of Rs. 520 lakhs and had approached his Portfolio Manager. The Portfolio Manager had advised Mr. Fed Up to invest in the following manner:

You are required to advise Mr. Fed Up in regard to the following, using Capital Asset Pricing Methodology:
(i) Expected return on the portfolio, if the Government Securities are at 8% and the Nifty is yielding 10%.
(ii) Advisability of replacing Security ‘Better’ with NIFTY. [Nov. 2012] [8 Marks]
Answer:
(i) Expected Return from Portfolio as per CAPM

Thus Expected Return from Portfolio 10.208% =10.21% (Rounded off)
Alternatively, it can be computed by calculating the weighted Beta and applying CAPM as follows:
Average β =
0.50 × \(\frac{60}{520}\) + 1.00 × \(\frac{80}{520}\) + 0.80 × \(\frac{100}{520}\) + 1.20 × \(\frac{120}{520}\) + 1.50 × \(\frac{160}{520}\) = 1.104
As per CAPM
= 8% + 1.104 (10% – 8%)
= 0.10208 i.e. 10.208%
(ii) As computed above the expected return from Better is 10% which is exactly the same as from Nifty, hence there will be no difference even if the replacement of security is made. The reason behind this is that the beta of security ‘Better’ is 1 which is same as that of market, so, it clearly indicates that this security shall yield same return as market return.
![]()
Question 4.
Mr. Ram is holding the following securities :
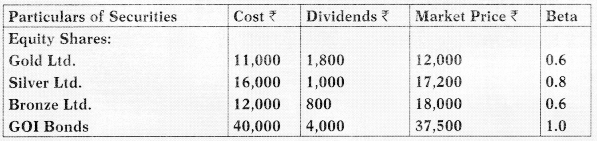
Calculate :
(i) Expected rate of return in each case, using the Capital Asset Pricing Model (CAPM).
(ii) Average rate of return, if risk free rate of return is 14%. [Nov. 2013] [8 Marks]
Answer:
Since, the market return is missing in the question, which is required to calculate the expected return of each security on the basis of CAPM, therefore, assuming the investments to be representing the market, first, average return on this portfolio is calculated.
(i) Expected Rate of Return
| Securities | Total Investments | Dividends | Capital Gains |
| Gold Ltd. | 11,000 | 1,800 | 1,000(12000 – 11000) |
| Silver Ltd. | 16,000 | 1,000 | 1,200(17200 – 16000) |
| Bronze Ltd. | 12,000 | 800 | 6,000(18000 – 12000) |
| GOI Bonds | 40,000 | 4,000 | (2,500) (37500 – 40,000) |
| 79,000 | 7,600 | 5,700 |
Expected rate of return on portfolio
\(\frac{\text { Dividend Earned }+ \text { Capital appreciation }}{\text { Initial investment }}\) × 100
= \(\frac{\text { Rs. } 7600+\text { Rs. } 5,700}{\text { Rs. } 79,000}\) × 100 = 16.84%
Now, taking 16.84% as market return the Rate of Return of each security using CAPM
= Rf + B (Rm – Rf)
| Gold Ltd. | 14+ 0.6 [16.84- 14] | = 14 + 1.70 | = 15.70% |
| Silver Ltd. | 14+ 0.8 [16.84- 14] | = 14 + 2.27 | = 16.27% |
| Bronze Ltd. | 14 +0.6 [ 16.84- 14] | = 14 + 1.70 | = 15.70% |
| GOI Bonds | 14+1.0 [16.84- 14] | = 14 + 2.84 | = 16.84 |
(ii) Expected Average Return of Portfolio (Based on simple average)
= \(\frac{15.70+16.27+15.70+16.84}{4}=\frac{64.51}{4}\) = 16.127%
Alternatively, It may also be calculated by first finding average Beta and then applying CAPM
Simple Average of Beta = \(\frac{0.6+0.8+0.6+1.0}{4}\)
= 0.75
14% + 0.75 (16.84% – 14%) = 14% + 2.13% = 16.13%
Question 5.
Mr. Shyam is holding the following securities:
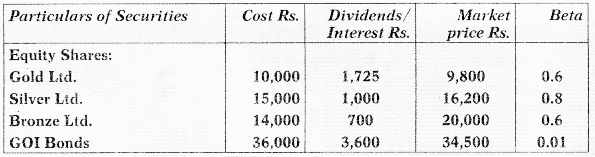
Average return of the portfolio is 15.7%, calculate:
(i) Expected rate of return in each, using the Capital Asset Pricing Model (CAPM).
(ii) RisL free rate of return. [May 2015] [8 Marks]
Answer:
| Particulars of Securities | Cost Rs. | Dividend | Capital Gain |
| Gold Ltd. | 10,000 | 1,725 | -200(9800- 10,000) |
| Silver Ltd. | 15,000 | 1,000 | 1,200 (16200- 15000) |
| Bronze Ltd. | 14,000 | 700 | 6,000 (20,000 – 14000) |
| GOI Bonds | 36,000 | 3,600 | -1,500 (34500-36000) |
| Total | 75,000 | 7,025 | 5,500 |
(i) Average rate of return on market portfolio
\(\frac{\text { Dividend Earned }+ \text { Capital appreciation }}{\text { Initial investment }}\) × 100
= \(\frac{R s \cdot 7,025+R s \cdot 5,500}{R s \cdot 75,000}\) × 100 = 16.7%
Rate of Return of each security using CAPM = Rf + B (Rm – Rf)
Note: The risk free rate is required to be calculated for the solution. As this is asked in the second part of the question, the figure of 14.69% has been taken from there.
Gold Ltd. = 14.69 + 0.6 (16.7 – 14.69) = 15.90%
Silver Ltd. = 14.69 + 0.8 (16.7 – 14.69) = 16.30%
Bronze Ltd. = 14.69 + 0.6 (16.7 – 14.69) = 15.90%.
GOL Bonds = 14.69 + 0.01 (16.7 – 14.69) = 14.72%
(ii) Risk free return
Simple Average of Beta = \(\frac{0.6+0.8+0.6+0.01}{4}\)
= 0.5025
Average return = Risk free return + Average Beta (Market return – Risk free return)
15.7 = Risk free return + 0.5025 (16.7 – Risk free return)
Risk free return = 14.69%.
Question 6.
Mr. X holds the following portfolio:
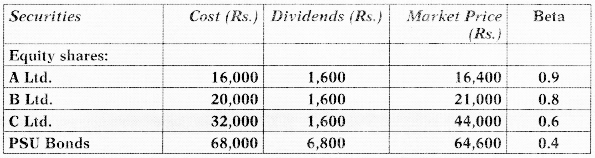
The risk-free rate of return is 12%
Calculate the following:
(i) The expected rate of return on his portfolio using Capital Asset Pricing Model (CAPM).
(ii) The average return on Ms portfolio. (Calculate up to two decimal points) [Nov. 2019] [8 Marks]
Answer:
The market return is missing in the question, which is required to calculate the expected return of portfolio on the basis of CAPM. Therefore, it has been assumed that the portfolio given in the question represents the market.
(i) Calculation of Expected Rate of Return
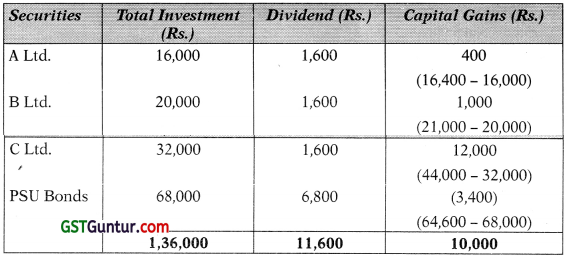
Expected rate of return on Portfolio
= \(\frac{\text { Dividend Earned }+ \text { Capital appreciation }}{\text { Initial investment }}\) × 100
= \(\frac{\text { Rs. } 11,600+\text { Rs. } 10,000}{\text { Rs. } 1,36,000}\) × 100 = 15.88%
Determination of Average Beta
Simple Average ol Beta = \(\frac{0.9+0.8+0.6+0.4}{4}\)
= 0.675
Alternatively, It may also be calculated by finding weighted average Beta and then applying CAPM
(i) Calculation of Expected Average Return of Portfolio (Using CAPM)
= Rf + B (Rm – Rf)
12% + 0.675 (15.88 – 12%) = 12% + 2.62% = 14.62%
(ii) Average Return of Portfolio :
= \(\frac{\text { Dividend Earned }+ \text { Capital appreciation }}{\text { Initial investment }}\) × 100
= \(\frac{\text { Rs. } 11,600+\text { Rs. } 10,000}{\text { Rs. } 1,36,000}\) × 100 = 15.88%
![]()
Question 7.
The following information is available in respect of Security A
| Equilibrium Return | 12% |
| Market Return | 12% |
| 6% Treasury Bond Trading at | 120 |
| Covariance of Market Return and Security Return | 196% |
| Coefficient of Correlation | 0.80 |
You are required to determine the Standard Deviation of Market Return and Security Return. [Nov. 2016] [5 Marks]
Answer:
First we shall compute the β of Security A
Since, 6% treasury bond is trading at Rs. 120, therefore, Risk Free Rate
= \(\frac{\text { Coupon Payment }}{\text { Current Market Price }}=\frac{6}{120}\) = 5%
Assuming equilibrium return to be equal to CAPM return then:
12% = Rf + βA (Rm – Rf)
12% = 5% + βA (12% – 5%)
Solving for βA:
βA = 1
(i) Standard Deviation of Market Return
βA = \(\frac{{Cov}_{A, m}}{\sigma_m^2}=\frac{196 \%}{\sigma_m^2}\)
σm2 = 196%
σm = \(\sqrt{196}\) = 14%
(ii) Standard Deviation of Security Return
βA = \(\frac{\sigma_A}{\sigma_m}\) × ρxm = \(\frac{\sigma_x}{14}\) × 0.8 = 1
σA = \(\frac{14}{0.80}\) = 17.50%
Question 8.
A company has a choice of investments between several different equity-oriented mutual funds. The company has an amount of ₹ 1 crore to invest. The details of the mutual funds are as follows:
| Mutual Fund | Beta |
| A | 1.6 |
| B | 1.0 |
| C | 0.9 |
| D | 2.0 |
| E | 0.6 |
Required:
(i) If the company invests 20% of its investment in the first two mutual funds and an equal amount in the mutual funds C, D and E, what ¡s the beta of the portfolio?
(ii) If the company Invests 15% of its investment in C, 15% in A, 10% In E and the balance In equal amount In the other two mutual funds, what is the beta of the portfolio?
(iii) If the expected return of market portfolio is 12% at a beta factor of 1.0, what will be the portfolios expected return in both the situations given above? [May 2008] [10 Marks]
Answer:
(i) Portfolio Beta is the weighted average of the Betas of various securities. When the investment in each MF is 20%, the weighted average of the Betas of various securities shall be the same as simple average and it is calculated as below:
Simple Average of Beta = \(\frac{1.6+1+0.9+2+0.6}{5}\) = 1.22
(ii) With varied percentage of investments, portfolio beta is calculated as follow:
| Investment | Beta (β) | (W) Investment (₹ Lacs) | Weight × Beta |
| A | 1.6 | 15 | 24 |
| B | 1 | 30 | 30 |
| C | 0.9 | 15 | 13.5 |
| D | 2 | 30 | 60 |
| E | 0.6 | 10 | 6 |
| 100 | 133.5 |
Weighted BETA = 1.335
(iii) Expected return of the portfolio with pattern of investment as in
case (i) 120/6 × 1.22 i.e. 14.64%
case (ii) 12% × 1.335 i.e., 16.02%
Question 9.
Consider the following information on two stocks, A and B.
| Year | Return on A (%) | Return of B(%) |
| 2006 | 10 | 12 |
| 2007 | 16 | 18 |
You are required to determine:
(i) The expected return on a portfolio containing A and B in the proportion of 40% and 60% respectively.
(ii) The Standard Deviation of return from each of the two stocks.
(iii) The covariance of returns from the two stocks.
(iv) Correlation coefficient between the returns of the two stocks.
(v) The risk of a portfolio containing A and B in the proportion of 40% and 60%. [Nov. 2008] [May 2018] [5 Marks]
Answer:
(i) Expected return of the stock A andB
E (A) = (10 + 16)/2 = 13%
E (B) = (12 + 18)/2 = 15%
Rp = \(\sum_{i=1}^N\)XiRi = 0.4 (13) + 0.6 (15) = 14.2%
(ii) Standard deviation of return from each stock.
Stock A:
Variance = \(\frac{\sum_{i=1}^n\left(x_i-\bar{X}\right)^2}{N}\)
Variance = 0.5 (10 – 13)2 + 0.5 (16 – 13)2 = 9
Standard deviation = √9 = 3%
Stock B:
Variance = 0.5 (12 – 15)2 + 0.5 (18 – 15)2 = 9
Standard deviation = 3%
(iii) Covariance of stocks A and B
Covariance = \(\frac{\sum_{i=1}^n\left(x_i-\bar{X}\right)\left(\mathbf{Y}_i-\bar{Y}\right)}{\mathbf{N}}\)
CovAB = 0.5 (10 – 13) (12 – 15) + 0.5 (16 – 13) (18 – 15) = 9
(iv) Correlation of coefficient
rAB = \(\frac{C o v_{A B}}{\sigma_A \sigma_\beta}=\frac{9}{3 \times 3}\) = 1
(v) Portfolio Risk
Portfolio Variance
σ2AB = WA2σA2 + WB2σB2 + 2WAWBσAσBr
σ = \(\sqrt{1.44+3.24+4.32}\) = 3%
Question 10.
Consider the following information on two stocks X and Y:
| Year | Return on X (%) | Return on Y (%) |
| 2008 | 12 | 10 |
| 2009 | 18 | 16 |
You are required to determine :
(i) The expected return on a portfolio containing X and Y in the proportion of 60% and 40% respectively.
(ii) The standard deviation of return from each of the two stocks.
(iii) The covariance of returns from the two stocks.
(iv) Correlation co-efficient between the returns of the two stocks.
(v) The risk of portfolio containing X and Y in the proportion of 60% and 40%. [Nov. 2010] [8 Marks]
Answer:
(i) Computation of Expected return of the stock X and Y:
E(X) = (12 + 18)/2 = 15%
E(Y) = (10 + 16)/2 = 13%
Rp = \(\sum_{i=1}^N\) XiRi = 0.6 (15)+ 0.4 (13) = 142%
(ii) Computation of Standard deviation of return from each of the two stock:
Stock X:
Variance = \(\frac{\sum_{i=1}^n\left(x_i-\bar{X}\right)^2}{N}\)
Variance = 0.5 (12 – 15)2 + 0.5 (18 – 15)2 = 9
Standard deviation = √9 = 3%
Stock Y:
Variance = \(\frac{\sum_{i=1}^n\left(Y_i-\bar{Y}\right)^2}{N}\)
Variance = 0.5 (10 – 13)2 + 0.5 (16 – 13)2 = 9
Standard deviation = √9 = 3%.
(iii) Computation of Covariance of Stock X and Y
Covariance = \(\frac{\sum_{i=1}^n\left(\mathrm{x}_i-\bar{X}\right)\left(\mathrm{Y}_i-\bar{Y}\right)}{\mathrm{N}}\)
Covxy = 0.5 (12 – 15) (10 – 13) + 0.5 (18 – 15) (16 – 13) = 9
(iv) Computation of Correlation of Coefficient
γxy = \(\frac{C O V_{x y}}{\sigma_x \sigma_y}=\frac{9}{3 \times 3}\) = 1
(v) Portfolio Risk
σp = \(\sqrt{\left((0.6)^2(3)^2+(0.4)^2(3)^2+2(0.6)(0.4)(3)(3)(1)\right)}\)
= \(\sqrt{3.24+1.44+4.32}\)
= √9 = 3%.
![]()
Question 11.
Mr. Gupta is considering investment in the shares of R. Ltd. He has the following expectations of return on the stock and the market:
| Probability | Return | |
| R.Ltd. | Market | |
| 0.35 | 30 | 25 |
| 0.30 | 25 | 20 |
| 0.15 | 40 | 30 |
| 0.20 | 20 | 10 |
You are required to:
(i) Calculate the expected return, variance and standard deviation for R.Ltd.
(ii) Calculate the expected return, variance and standard deviation for the market.
(iii) Find out the beta Co-efficient for R Ltd. shares. [Nov. 2018 old syllabus][8 Marks]
Answer:
(i) Calculation of expected return, variance and standard deviation of R Ltd.
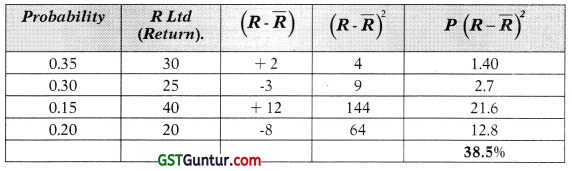
Expected. Return
= 0.35 (30) + 0.30 (25) + 0.15 (40) + 0.20 (20)
= 10.5 + 7.5 + 6 + 4
= 28%
Variance = ΣP1(Xi – x̄)2
= 38.5%
σR = \(\sqrt{38.5}\) = 6.205%
(i) Calculation of expected return, variance andstandard deviation of Market.
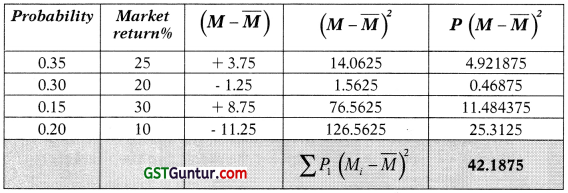
Expected Return market
= 0.35 (25) + 0.30 (20) + 0.15 (30) + 0.20 (10)
= 8.75 + 6 + 4.5 + 2
= 21.25%
Variance = ΣP1(Xi – x̄)2
= 42.1875%
σM = \(\sqrt{42.1875}\) = 6.4952%
(ii) The Beta coefficient of R Ltd. shares:
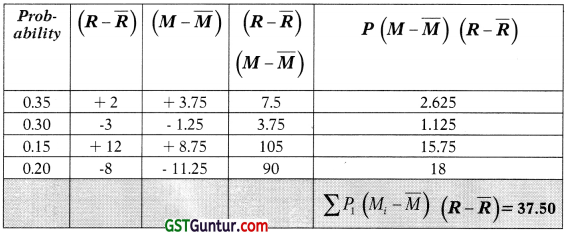
Beta = \(\frac{\text { Covariance }}{\sigma_M{ }^2}\)
\(\frac{37.50}{6.4952^2}\) = 0.888
Question 12.
An investor is holding 5,000 shares of X Ltd. Current year dividend rate is Rs. 3/share. Market price of the share is Rs. 40 each. The investor is concerned about several factors which are likely to change during the next financial year as indicated below:
| Current Year | Next Year | |
| Dividend paid/anticipated per share (Rs.) | 3 | 2.5 |
| Risk free rate | 12% | 10% |
| Market Risk Premium | 5% | 4% |
| Beta Value | 1.3 | 1.4 |
| Expected growth | 9% | 7% |
In view of the above, advise whether the investor should buy, hold or sell the shares, [Nov. 2014] [6 Marks]
Answer:
The Investor should take the decision to buy, hold or sell the shares on the basis of change in price and rate of return.
Existing rate of return
= Rf + Beta (Rm – Rf)
= 1296 + 1.3 (596) = 18.5%
Revised rate of return
= 10% + 1.4 (4%) = 15.60%
Price of share (original)
P0 = \(\frac{D(1+g)}{K_e-g}=\frac{3(1.09)}{0.185-0.09}=\frac{3.27}{0.095}\) = Rs. 34.42
Price of share (Revised)
P0 = \(\frac{2.50(1.07)}{0.156-0.07}=\frac{2.675}{0.086}\) = Rs. 31.10
The current market price of share is Rs. 40. It is higher in comparison to current equilibrium price of Rs. 34.42 and revised equity price of Rs. 31.10. Under this situation investor should sell the share.
Question 13.
The following information are available with respect of Krishna Ltd.
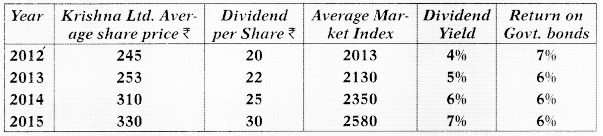
Compute Beta Value of the Krishna Ltd. at the end of 2015 and state your observation. [May 2017] [8 Marks]
Answer:

Returns from Market Index
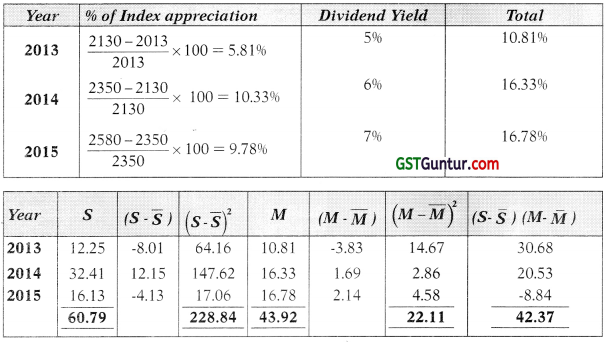
Average Return of Krishna Ltd. = \(\frac{60.79}{3}\) = 20.26%
Average Market Return = \(\frac{43.92}{3}\) = 14.64%

As the Beta of the stock is 1.92 which is relatively high, therefore, the stock is a risky investment
![]()
Question 14.
Following is the data regarding six securities:

(i) Which of three securities will be selected?
(ii) Assuming perfect correlation, analyse whether it is preferable to invest 80% in security U and 20% in security W or to invest 100% in Y. [Nov. 2009] [6 Marks]
Answer:
(i) When we make risk-return analysis of different securities from U to Z, we can observe that security U gives a return of 10% at risk level of 5%. Simultaneously securities V and Z give the same return of 10% as of security U, but their risk levels are 6% and 7% respectively. Security X is giving only 5% return for the risk rate of 5%. Hence, security U dominates securities V, X and Z.
Securities W and Y offer more return but it carries higher level of risk. Hence securities U, W and Y can be selected based on individual preferences.
(ii) In a situation where the perfect positive correlation exists between two securities, their risk and return can be averaged with the proportion.
Assuming the perfect correlation exists between the securities U and W, average risk and return of U and W together for proportion 4 : 1 is calculated as follows:
Risk = (4 × 5% + 1 × 13%) ÷ 5 = 6.6%
Return = (4 × 10% + 1 × 15%) ÷ 5 = 11%
| Therefore: | 80% U | 100%Y |
| 20% V | – | |
| Risk | 6.6% | 6% |
| Return | 11% | 11% |
Where we compare risk of 6.6% and return of 11% with security Y with 6% risk and 11% return, security Y is preferable over the portfolio of securities U and W in proportion of 4:1.
Question 15.
The returns on stock A and market portfolio for a period of 6 years are as follows:
| Year | Return on A (%) | Return on market portfolio (%) |
| 1 | 12 | 8 |
| 2 | 15 | 12 |
| 3 | 11 | 11 |
| 4 | 2 | -4 |
| 5 ‘ | 10 | 9.5 |
| 6 | -12 | -2 |
You are required to determine:
(i) Characteristic line for stock A
(ii) The systematic and unsystematic risk of stock A. [May 2009] [8 Marks]
Answer:
Characteristic line is given by
Y = α + βRm
βi = \(\frac{\sum x y-n \bar{x} \bar{y}}{\sum x^2-n(\bar{x})^2}\)
αi = ȳ – βx̄
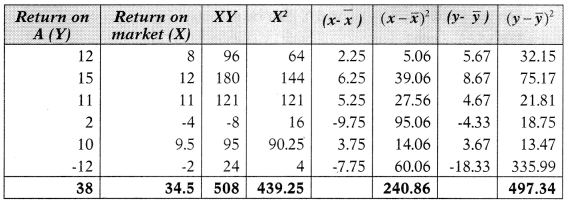

α = ȳ – βx̄ = 6.33 – 1.202(5.75) = -0.58
Hence the characteristic line is -0.58 + 1.202 (Rm)
Market variance = σm2 = \(\frac{\sum(x-\bar{x})^2}{n}=\frac{240.86}{6}\) = 240,86 =3 40.14(%)
Total Risk of Stock = σs2 = \(\frac{\sum(y-\bar{y})^2}{n}=\frac{497.34}{6}\) = 82.89(%)
Systematic Risk of the stock = βi2σm2 = (1.202)2 × 40.14 = 57.99(9-6)
Therefore, Unsystematic Risk = Total Risk – Systematic Risk
= 82.89 – 57.99 = 24.90(%)
Question 16.
The returns and market portfolio for a period of four years are as under:
| Year | % Return of Stock B | % Return on Market Portfolio |
| 1 | 10 | 8 |
| 2 | 12 | 10 |
| 3 | 9 | 9 |
| 4 | 3 | -1 |
For stock B, you are required to determine:
(i) characteristic line; and
(ii) the Systematic and Unsystematic risk.
Answer:

β = 0.740
(i) Characteristic line of stock B
Y = a + bX
a = ȳ – bx̄
= 8.5 – (0.74 × 6.5)
= 3.69
Characteristic line y = 3.69 4 0.74 Rm
(ii) The Systematic and Unsystematic Risk
| Variance approach | |
| Total Risk of stock B | 11.25% |
| Systematic Risk | β2 × σm2 = (0.74)2 σ 19.25 = 10.54 |
| Unsystematic Risk | Total risk-systematic risk = 0.71% |
| (11.25%- 10.54%) |
Question 17.
X Co. Ltd. invested on 1.4.2009 in certain equity shares as below:
| Name of Co. | No. of shares | Cost (Rs.) |
| M Ltd. | 1,000 (Rs. 100 each) | 2,00,000 |
| N Ltd. | 500 (Rs. 10 each) | 1,50,000 |
In September 2009,10% dividend was paid out by M Ltd. and in October 2009, 30% dividend paid out by N Ltd. on 31.3.2010 market quotations showed a value of Rs. 220 and Rs. 290 per share for M Ltd. and N Ltd. respectively. On 1.4.2010, investment advisors indicate (a) that the dividends from M Ltd. and N Ltd. for the year ending 31.3.2011 are likely to be 20% and 35%, respectively and (b) that the probabilities of market quotations on 31.3.2011 are as below:
| Probability Factor | Price/share of M Ltd. | Price/share of N Ltd. |
| 0.2 | 220 | 290 |
| 0.5 | 250 | 310 |
| 0.3 | 280 | 330 |
You are required to:
(i) Calculate the average return from the portfolio for the year ended 31.3.2010;
(ii) Calculate the expected average return from the portfolio for the year 2010-11; and
(iii) Advise X Co. Ltd., of the comparative risk in the two investments by calculating the standard deviation in each case. [May 2008] [8 Marks]
Answer:
(i) Average rate of return of the portfolio
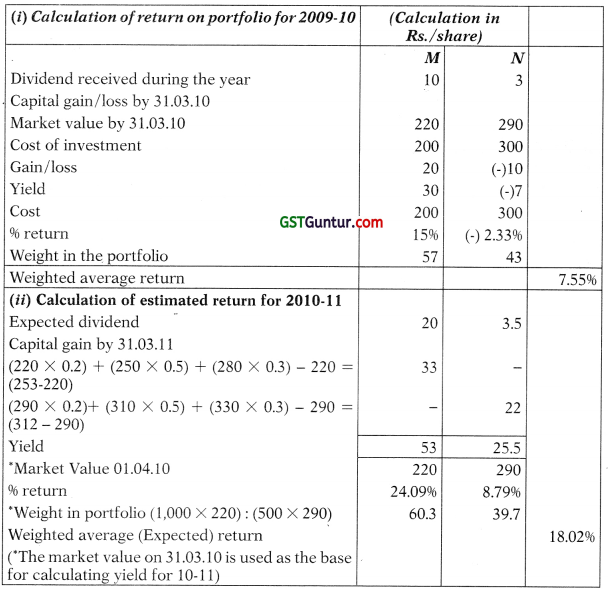
(iii) Calculation of Standard Deviation
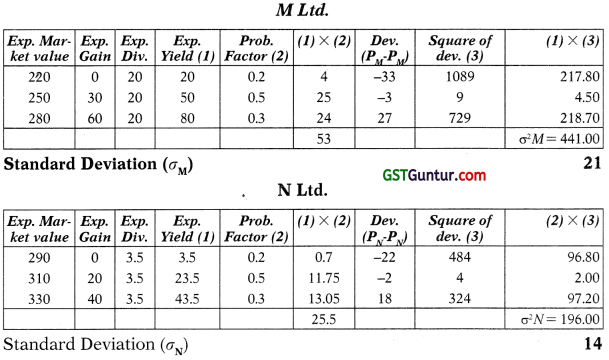
Standard Deviation (σM) 14
Share of company M Ltd. is more risky as the S.D. is more than company N Ltd.
Question 18.
An investor holds two stocks A and B. An analyst prepared ex-ante probability distribution for the possible economic scenarios and the conditional returns for two stocks and the market index as shown below:
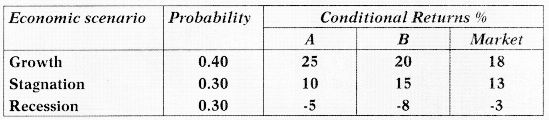
The risk free rate during the next year is expected to be around 11%. Determine whether the investor should liquidate his holdings in stocks A and B or on the contrary make fresh investments in them. CAPM assumptions are holding true. [Nov. 2009] [10 Marks]
Answer:
Expected Return on stock A = E (A) = V P.A.
(0.40) (25) + 0.30(10) + 0.30 (-5) = 11.5%
Expected Return on ‘B’
(0.40 × 20) + (0.30 × 15) + 0.30 × (-8) = 10.1%
Expected Return on Market index
(0.40 × 18) + (0.30 × 13) + 0.30 × (-3) = 10.2%
Variance of Market index
(18 – 10.2)2 (0.40) + (13 – 10.2)2 (0.30) + (-3 – 10.2)2 (0.30)
= 24.34 + 2.35 + 52.27 = 78.96%
Covariance of stock A and Market Index M
Cov. (AM) = Σ [Ai – E(A)] [Mi – E(M)]P
(25-11.5) (18-10.2) (0.40) + (10 – 11.5) (13-10.2) (0.30) + (-5-11.5) (-3-10.2) (0.30)
= 42.12 + (-1.26) + 65.34 = 106.20
Covariance of stock B and Market index M
(20 – 10.1) (18 – 10.2) (0.40) + (15 – 10.1) (13 – 10.2) (0.30) + (-8 – 10.1) (-3-10.2) (0.30)
= 30.89 + 4.12 + 7167
= 106.68
Beta for stock A = \(\frac{{CoV}(A M)}{V A R(M)}=\frac{106.20}{78.96}\) = 1.345
Beta for Stock B = \(\frac{{CoV}(B M)}{Var(M)}=\frac{106.20}{78.96}\) = 1.351
Required Return for A
R (A) = Rf + p (M – Rf)
11% + 1.345 (10.2 – 11)% = 9.924%
Required Return forB
11% + 1.351 (10.2 – 11)% = 9,92%
Alpha for Stock A
E (A) – R (A) ie. 11.5% – 9.924% = 1.576%
Alpha for Stock B
E (B) – R (B) ie. 10.1% – 9,92% = 0.18%
Since stock A and B both have positive Alpha, therefore, they are UNDERPRICED. The investor should make fresh investment in them.
![]()
Question 19.
An investor has two portfolios known to be on minimum variance set for a population of three securities A, B and C having below-mentioned weights:

It is supposed that there are no restrictions on short sales.
(i) What would be the weight for each stock for a portfolio constructed by investing Rs. 5,000 in portfolio X and Rs. 3,000 in portfolio Y?
(ii) Suppose the investor invests Rs. 4,000 out of Rs. 8,000 in security A. How he will allocate the balance between security B and C to ensure that his portfolio is on minimum variance set? [May 2009] [6 Marks]
Answer:
(i) Investment committed to each security would be:
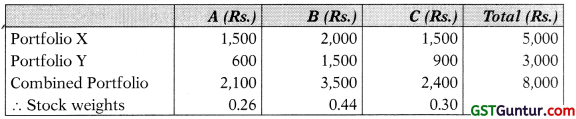
(ii) The equation of critical line takes the following from:-
WB = a + bWA
Substituting the values of WA & WB from portfolio X and Y in above equation, we get
0.40 = a + 0.30b,
and 0.50 = a + 0.20b
Solving above equation we obtain the slope and intercept, a = 0.70 and b = -1 and thus, the critical line is
WB = 0.70 – WA
If half of the funds is invested in security A then,
WB = 0.70 – 0.50 = 0.20
Since WA + WB + WC = 1
WC = 1 – 0.50 – 0.20 = 0.30
∴ Allocation of funds to security B = 0.20 × 8,000 = Rs. 1,600, and
Security C = 0.30 × 8,000 = Rs. 2,400
Question 20.
A study by a Mutual fund has revealed the following data in respect of three securities:
| Security | σ (%) | Correlation with Index, Pm |
| A | 20 | 0.60 |
| B | 18 | 0.95 |
| C | 12 | 0.75 |
The standard deviation of market portfolio (BSE Sensex) is observed to be 15%
(i) What is the sensitivity of returns of each stock with respect to the market?
(ii) What are the covariances among the various stocks?
(iii) What would be the risk of portfolio consisting of all the three stocks equally?
(iv) What is the beta of the portfolio consisting of equal investment in each stock?
(v) What is the total, systematic and unsystematic risk of the portfolio in (iv)? [Nov. 2009] [8 Marks]
Answer:
(i) Sensitivity of each stock with market is given by its beta.
Standard deviation of market Index =15%
Variance of market Index = 0.0225
Beta of stocks = rσi/ σm
A = 0.60 × 20/15 = 0.80
B = 0.95 × 18/15 = 1.14
C = 0.75 × 12/15 = 0.60
(ii) Covariance between any 2 stocks = β1β2σ2m
Covariance matrix
| Stock/Beta | 0.80 | 1.14 | 0.60 |
| A | 400.00 | 205.200 | 108.000 |
| B | 205.200 | 324.000 | 153.900 |
| C | 108.000 | 153.900 | 144.000 |
(iii) Total risk of the equally weighted portfolio (Variance)
= 400(1 /3)2 + 324(1 /3)2 + 144(1 /3)2 + 2 (205.20) (1/3)2 + 2 (108.0) (1/3)2 + 2(153.900) (1/3)2
= 200.244
(iv) β of equally weighted portfolio = βp = Σβ/N = \(\frac{0.80+1.14+0.60}{3}\)
= 0.8467
(v) Systematic Risk β2am2 = (0.8467)2 (15)2 = 161.302
Unsystematic Risk = Total Risk – Systematic Risk
= 200.244- 161.302 = 38.942
Question 21.
Following are risk and return estimates for two stocks :
| Stock | Expected returns (%) | Beta | Specific SD of expected return (%) |
| A | 14 | 0.8 | 35 |
| B | 18 | 1.2 | 45 |
The market index has a Standard Deviation (SD) of 25% and risk free rate on Treasury Bills is 6%.
You are required to calculate :
(i) The standard deviation of expected returns on A and B.
(ii) Suppose a portfolio is to be constructed with the proportions of 25%, 40% and 35% in stock A, B and Treasury Bills respectively, what would be the expected return, standard deviation of expected return of the portfolio ? [Nov. 2019] [8 Marks]
Answer:
(i) The standard deviation of expected returns on A and B is 35% and 45% as already given in the question.
(ii) Expected return and risk of portfolio with investment in A 25%, in B 40% and treasury bills 35%.
Return = W1RA + W2RB + W3RTr.Bills
Risk = 0.25 (14) + 0.40 (18) + 0.35 (6) = 12.8%
Risk = \(\sqrt{\sigma_1{ }^2 \mathrm{~W}_1{ }^2+\sigma_2{ }^2 \mathrm{~W}_2{ }^2+\sigma_3{ }^2+\mathrm{W}_3{ }^2+2 \mathrm{w}_1 \mathrm{w}_2 {Cov}_{12}+2 \mathrm{w}_1 \mathrm{w}_3 {Cov}_{13}+2 \mathrm{w}_2 \mathrm{w}_3 {Cov}_{23}}\)
Calculation of Covariance between A and B = Beta (A) × Beta (B) × Market
variance Covariance between any 2 stocks = β1β2σ2m
= 0.8 × 1.2 × 252 = 600
As σ3 =0 Being treasury bills and r23 and r13 is also 0, the formula reduces to:
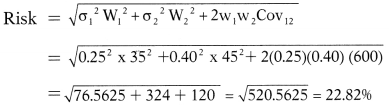
Question 22.
Mr. Tempest has the following portfolio of four shares:
| Name | Beta | Investment Rs. Lac |
| Oxy Rin Ltd. | 0.45 | 0.80 |
| Boxed Ltd. | 0.35 | 1.50 |
| Square Ltd. | 1.15 | 2.25 |
| Ellipse Ltd. | 1.85 | 4.50 |
The risk free rate of return is 7% and the market rate of return is 14% [May 2011] [5 Marks]
Required:
(i) Determine the portfolio return,
(ii) Calculate the portfolio Beta.
Answer:
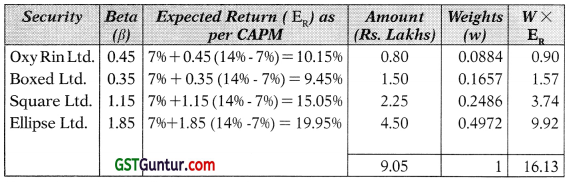
Therefore the Portfolio return is 16.13%
Alternatively, the return may also be calculated after calculating the weighted Beta and using it in CAPM. WeightedBeta= 1.3035 as calculated in Part (ii) of the question.
(i) Portfolio Return using CAPM formula will be as follows:
E = Rf + Beta (R – Rf)
= 7% + 1.3035 (14% – 7%) = 7% + 1.3035(7%)
= 7% + 9.1245% = 16.1245%
(ii) Portfolio Beta
0.45(0.884) + 0.35(0.1657) + 1.15(0.2486) 4- 1.85 (0.4972)
= 1.3035
![]()
Question 23.
A has portfolio having following features:

You are required to find out the risk of the portfolio if the Standard deviation of the market index (σm) is 18%. [May 2012] [8 Marks]
Answer:
The variance of portfolio Return = Systematic Variance + Unsystematic Variance.

Systematic Variance = (1.295)2 x (18)2= 543.36, Weighted unsystematic
variance =17.755
Therefore, Standard deviation of the portfolio (cr2) = 543.36 + 17.75 =561.11%
Question 24.
Following are the details of a portfolio consisting of 3 shares:

Standard Deviation of Market Portfolio Returns = 12%
You are required to calculate the following:
(i) The Portfolio Beta.
(ii) Residual variance of each of the three shares.
(iii) Portfolio variance using Sharpe Index Model. [May 2019] [8 Marks]
Answer:
(i) Portfolio Beta
0.30 × 0.5 + 0.50 × 0.60 + 0.20 × 1.20 = 0.69
(ii) Residual Variance
To determine Residual Variance first of all we shall compute the Systematic Risk as follows:
βx2 × σN2 = (0.50)2 (0.12)2 = 0.0036
βy2 × σN2 = (0.60)2 (0.12)2 = 0.005184 = 0.0052 approx.
βz2 × σN2 = (1.20)2 (0.12)2 = 0.020736 = 0.0207 approx
Residual Variance (Total risk – Systematic risk)
X Ltd. = 0.020 – 0.0036 = 0.0164
Y Ltd. = 0.010 – 0.0052 = 0.0048
Z Ltd. = 0.120 – 0.0207= 0.0993
(iii) Portfolio variance using Sharpe Index Model /
= Systematic risk + Unsystematic risk
Systematic Variance of Portfolio = βp2 × σN2 (0.69)2 × (0.12)2 = 0.006856
Unsystematic Variance of Portfolio is the weighted average of the residual risk of individual securities.
Unsystematic Variance of Portfolio = (0.0164) × (0.30)2 + (0.0048) × (0.50)2 + (0.0993) × (0.20)2
= 0.001476 + 0.0012 + 0.003972 = 0.006648
Total Variance = 0.006856 + 0.006648 = 0.013 504 = 135.04%
Question 25.
Following are the details of a portfolio consisting of three shares:

Standard Deviation of Market Portfolio Returns = 10%
You are given the following additional data:
Covariance (A, B) = 0.030
Covariance (A, C) = 0.020
Covariance (B, C) = 0.040
Calculate the following:
(i) The Portfolio Beta
(ii) Residual variance of each of the three shares
(iii) Portfolio variance using Sharpe Index Model
(iv) Portfolio variance (on the basis of modern portfolio theory given by Markowitz) [May 2015] [8 Marks]
Answer:
(i) Portfolio Beta [It is the weighted average of Beta]
0.20 × 0.40 + 0.50 × 0.50 + 0.30 × 1.10 = 0.66
(ii) Residual Variance or unsystematic risk
To determine Residual Variance first of all we shall compute the Systematic Risk as follows:
βA2 × σN2 =(0.40)2 (0.1)2 = 0.0016
βB2 × σN2 =(0.50)2 (0.1)2 = 0.0025
βC2 × σN2 = (1.10)2 (0.1)2 = 0.0121
Residual Variance (Total risk – Systematic risk)
A 0.015-0.0016 = 0.0134
B 0.025 – 0.0025 = 0.0225
C 0.100-0.0121 =0.0879
(iii) Portfolio variance using Sharpe Index Model
Systematic Variance of Portfolio = βp2 × σN2 (0.66)2 × (0.10)2 = 0.004356
The unsystematic variance of the portfolio is the weighted average of individual residual variance of securities in the portfolio.
Unsystematic Variance of Portfolio = (0.0134) × (0.20)2 + 0.0225 × (0.50)2 + 0.0879 × (0.30)2 = 0.014072
Total Variance = 0.004356 + 0.014072 = 0.018428
(iv) Portfolio variance on the basis of Markowitz Theory
= (WA × WA × σA2) (WA × WB × COVAB) + (WA × WC × CovAC) + (WB × WA × CovAB) + (WB × WB × σ2B) + (WB × WC × CovBC) + (WC × WA × CovCA) + (WC × WB × CovCB) + (WC × WC × σ2B)
= (0.20 × 0.20 × 0.015) + (0.20 × 0.50 × 0.030) + (0.20 × 0.30 × 0.020) + (0.20 × 0.50 × 0.030) + (0.50 × 0.50 × 0.025) + (0.50 × 0.30 × 0.040) + (0.30 × 0.20 × 0.020) + (0.30 × 0.50 × 0.040) + (0.30 × 0.30 × 0.10)
= 0.0006 + 0.0030 + 0.0012 + 0.0030 + 0.00625 + 0.0060 + 0.0012 + 0.0060 + 0.0090
= 0.0363
Question 26.
A Portfolio Manager (PM) has the following four stocks in his portfolio:

Compute the following: Portfolio beta. [Nov. 2011][8 Marks]
Answer.
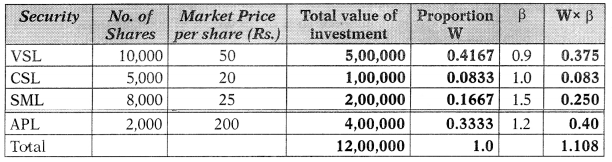
Question 27.
Mr. X owns a portfolio with the following characteristics:
| Security A | Security B | Risk Free security | |
| Factor 1 sensitivity | 0.80 | 1.50 | 0 |
| Factor 2 sensitivity | 0.60 | 1.20 | 0 |
| Expected Return | 15% | 20% | 10% |
It is assumed that security returns are generated by a two-factor model.
(i) If Mr. X has Rs. 1,00,000 to invest and short sells Rs.50,000 of security B and purchases Rs. 1,50,000 of security A what is the sensitivity of Mr. X‘s portfolio to the two factors?
(ii) If Mr. X borrows Rs. 1,00,000 at the risk free rate and invests the amount he borrows along with the original amount of Rs. 1,00,000 in security A and B in the same proportion as described in part (i), what is the sensitivity of the portfolio to the two factors?
(iii) What is the expected return premium of factor 2? [May 2009] [8 Marks]
Answer:
(i) Mr. X’s position in the two securities are + 1.50 in security A and -0.5 in security B.
Hence the portfolio sensitivities to the two factors:-
Factor 1 – 1.50 × 0.80 + (-0.50 × 1.50) = 0.45
Factor 2 = 1.50 × 0.60 + (0.50 × 1.20) = 0.30
(ii) Mr. X’s current position:-
Security A Rs. 3,00,000/Rs. 1,00,000 – 3
Security B -Rs. 1,00,000/Rs. 1,00,000 = -1
Risk free asset – Rs.100000/Rs.100000 = -1
Factor 1 = 3.0 × 0.80 + (-1 × 1.50) + (-1 × 0) = 0.90
Factor 2 = 3.0 × 0.60 + (-1 × 1.20) + (-1 × 0) = 0.60
(iii) Expected Return = Risk Free Rate of Return + Risk Premium
Let λ1 and λ2 are the Value of risk premium of Factor 1 and Factor 2 respectively. Since, the return of security A is 15% with sensitivity of 0.8 and 0.6 to Factor 1 and Factor 2 and the return of security B is 20°n with sensitivity of 1.5 and 1.2 to Factor 1 and Factor 2, therefore,
15 = 10+ 0.80 λ1 + 0.60 λ2
20= 10+ 1.50 λ1 +1.20 λ2
On solving the two equations simultaneously, the value of λ1 = 0, and the ’premium of securities A & B shall be totally because of λ1 and which is as follows:
Security A Risk premium
Total Return = 15%
Risk Free Return = 10%
Risk Premium = 5%
Security B Risk premium
Total Return = 20%
Risk Free Return = 10%
Risk Premium = 10%
5 = 0.60 λ1
10 = 1.20 λ2
Therefore, Risk premium of factor 2 = λ2 = 5/0.6 = 8.33
Question 28.
Mr. Kapoor owns a portfolio with the following characteristics:
| Security X | Security Y | Risk free Security | |
| Factor 1 sensitivity | 0.75 | 1.50 | 0 |
| Factor 2 sensitivity | 0.60 | 1.10 | 0 |
| Expected Return | 15% | 20% | 10% |
It is assumed that security returns are generated by a two factor model.
(i) If Mr. Kapoor has ₹ 1,00,000 to invest and sells short ₹ 50,000 of security Y and purchases ₹ 1,50,000 of security X, what is the sensitivity of Mr. Kapoor’s portfolio to the two factors?
(ii) If Mr. Kapoor borrows Rs. 1,00,000 at the risk free rate and invests the amount he borrows along w ith the original amount of ₹ 1,00,000 in security X and Y in the same proportion as described in part (i), what is the sensitivity of the portfolio to the two factors?
(iii) What is the expected return premium of factor 2? [Nov. 2018][8 Marks]
Answer:
(i) Mr. Kapoor’s position in the two securities are + 1.50 in security A and -0.5 in security B. Hence, the portfolio sensitivities to the two factors are:-
Factor 1 = 1.50 × 0.75 + (-0.50 × 1.50) = 0.375
Factor 2 = 1.50 × 0.60 + (-0.50 × 1.10) = 0.350
(ii) Mr. Kapoor’s changed position:-
Security A = ₹ 3,00,000/₹ 1,00,000 × 3
Security B = ₹ 1,00,000/₹ 1,00,000 = -1
Risk free asset – ₹ 100000/₹ 100000 = -1
Factor 1 = 3.0 × 0.75 + (-1 × 1.50) + (-1 × 0) = 0.75
Factor 2 = 3.0 × 0.60 + (-1 × 1.10) + (-1 × 0) = 0.70
(iii) Expected Return = Risk Free Rate of Return + Risk Premium
Let λ1 and λ2 are the Value of risk premium of Factor 1 and Factor 2 respectively. Since, the return of security A is 15% with sensitivity of 0.75 and 0.6 to factor 1 and factor 2 and the return of security B is 20% with sensitivity of 1.5 and 1.1 to facto)’ 1 and factor 2, therefore,
15 = 10 + 0.75λ1 + 0.60 λ2
20 = 10 + 1.50 λ1 + 1.10 λ2
On solving the two equations simultaneously, the value of λ2 = 0, and the – premium of securities A & B shall be totally because of λ1 and which is as follows:
| Security A Risk premium | Security B Risk premium |
| Total Return = 15% | Total Return = 20% |
| Risk Free Return =10% | Risk Free Return = 10% |
| Risk Premium = 5% | Risk Premium = 10% |
5 = 0.75 λ1
10= 1.50 λ1
Therefore, Risk premium of factor 1 = λ1 = 5/0.75 = 6.66% and the expected risk premium of factor 2 is 0.
![]()
Question 29.
Mr. Tamarind intends to invest in equity shares of a company the value of which depends upon various parameters as mentioned below:
| Factor | Beta | Expected value in % | Actual value in % |
| GNP | 1.20 | 7.70 | 7.70 |
| Inflation | 1.75 | 5.50 | 7.00 |
| Interest rate | 1.30 | 7.75 | 9.00 |
| Stock market index | 1.70 | 10.00 | 12.00 |
| Industrial production | 1.00 | 7.00 | 7,50 |
If the risk free rate of interest be 9.25% how much is the return of the share under Arbitrage Pricing Theory? [May 2011] [5 Marks]
Answer:
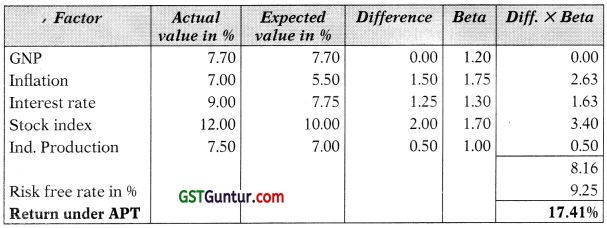
Question 30.
Indira has a fund of ₹ 3 lacs which she wants to invest in share market with re-balancing target after every 10 days to start with for a period of one month from now. The present NIFTY is 5326. The minimum NIFTY within a month can at most be 4793.4. She wants to know as to how she should re-balance her portfolio under the following situations, according to the theory of Constant Proportion Portfolio Insurance Policy, using “2” as the multiplier:
1. Immediately to start with.
2. 10 days later-being the 1st day of re-balancing if NIFTY falls to 5122.96.
3. 10 days further from the above date if the NIFTY touches 5539.04.
For the sake of simplicity, assume that the value of her equity component will change in tandem with that of the NIFTY and the risk free securities in which she is going to invest will have no Beta. [May 2012] [8 Marks]
Answer:
Maximum decline in one month = \(=\frac{5,326-4793.40}{5,326}\) × 100 = 10%
(1) Immediately to start with
Investment in equity = Multiplier × (Portfolio value – Floor value)
= 2 (3,00,000 – 2,70,000) = ₹ 60,000
Indira may invest ₹ 60,000 in equity and balance in risk free securities.
(2) After 10 days
Value of equity = 60,000 × 51.22.96/5326 = ₹ 57,713
Value of risk free investment = ₹ 2,40,000
Total value of portfolio = ₹ 2,97,713
Investment in equity = Multiplier × (Portfolio value – Floor value)
= 2 (2,97,713 – 2,70,000) = ₹ 55,426
Revised Portfolio:
Equity = ₹ 55,426
Risk Free Securities = ₹ 2,97,713 – ₹ 55,426 = ₹ 2,42,287
Ms. Indira should reduce her investments in equity from ₹ 57,713 to ₹ 55,426 by selling equity worth ₹ 2,287 and investing in risk free securities.
(3) After another 10 days
Valueofequity = 55,426 × 5539.04/5122.96 = ₹ 59,928
Value of risk free investment = ₹ 2,42,287
Total value of portfolio = ₹ 3,02,215
Investment in equity = Multiplier * (Portfolio value – Floor value)
= 2 (3,02,215 – 2,70,000) = ₹ 64,430
Revised Portfolio:
Equity = ₹ 64,430
Risk Free Securities = 3,02,215 – ₹ 64,430 = ₹ 2,37,785
The investor should off-load ₹ 4,502 of risk free securities and divert to Equity.
Question 31.
Ms. Sunidhi is working with an MNC at Mumbai. She is well versant with the portfolio management techniques and wants to test one of the techniques on an equity fund she has constructed and compare the gains and losses from the technique with those from a passive buy and hold strategy. The fund consists of equities only and the ending NAV’s of the fund she constructed for the last 10 months are given below:
| Month | Ending NAV (₹/unit) |
| December 2008 | 40.00 |
| January, 2009 | 25.00 |
| February, 2009 | 36.00 |
| March, 2009 | 32.00 |
| April, 2009 | 38.00 |
| May, 2009 | 37.00 |
| June, 2009 | 42.00 |
| July, 2009 | 43.00 |
| August, 2009 | 50.00 |
| September, 2009 | 52.00 |
Assume Sunidhi had invested a notional amount of ? 2 lakhs equally in the equity fund and a conservative portfolio (of Bonds) in the beginning of De-cember 2008 and the total portfolio was being rebalanced each time the NAV of the fund increased or decreased by 15%.
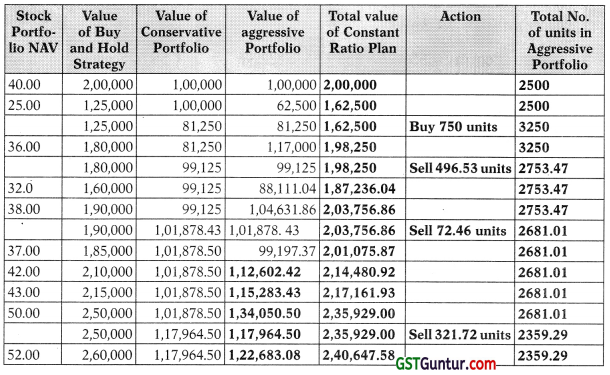
You are required to determine the value of the portfolio for each level of NAV following the Constant Ratio Plan. [Practice Question]
Answer:
Question 32.
Details about portfolio of shares of an investor is as below:
| Shares | No. of shares (lakh) | Price per share | Beta |
| A Ltd. | 3.00 | ₹ 500 | 1.40 |
| B Ltd. | 4.00 | ₹ 750 | 1.20 |
| C Ltd. | 2.00 | ₹ 250 | 1.60 |
The investor thinks that the risk of portfolio is very high and wants to reduce the portfolio beta to 0.91. He is considering two below’ mentioned alternative strategies:
(i) Dispose off a part of his existing portfolio to acquire risk free securities, or
(ii) Take appropriate position on Nifty Futures which are currently traded at ₹ 8,125 and each Nifty points is worth ₹ 200.
You are required to determine:
(1) portfolio beta,
(2) the value of risk free securities to be acquired,
(3) the number of shares of each company to be disposed off,
(4) the number of Nifty contracts to be bought/sold; and
(5) the value of portfolio beta for 2% rise in Nifty. [Nov. 2016] [8 Marks]
Answer:
Alternative 1 to dispose part of his existing Portfolio.
(1) Portfolio Beta :
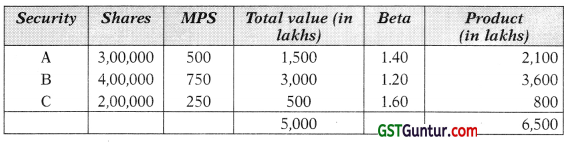
Portfolio Beta = \(\frac{6,500}{5,000}\) = 1.3
(2) Let amount of risk free security to be purchase for β = 0.91 be x
| Investment | Beta | Weights | Product |
| Risk free | 0 | w | 0 |
| Portfolio | 1.3 | 1-w | 1.3- 1.3 w |
| Total | 1 | 1.3 – 1.3w |
Portfolio Beta = 0.91 = \(\frac{1.3-1.3 w}{1}\)
w = 0.3 or 30%
Amount to be invested in risk-free securities 30% of 5,000 lakhs = 1,500 lakhs.
(3) No. of shares to be sold
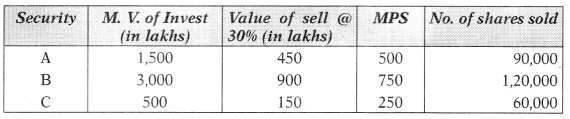
Alternative – (ii) to use Nifty futures
(4) No. of Nifty Futures to be traded
No. of contracts = Portfolio value × \(\frac{\text { Desired } \beta \text { of Portfolio }}{\text { Value of future contract }}\)
= 5,000 lakhs × \(\frac{1.30-0.91}{8,125 \times 200}\) = 120 contracts
In order to bring down the Beta of the portfolio from 1.3 to 0.91, opposite position should be taken in Nifty futures. Therefore, 120 contracts of Nifty futures should be sold.
(5) New portfolio Beta after 2% Rise in Nifty
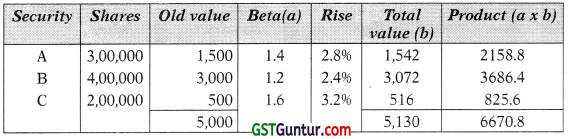
β = \(\frac{6670.8}{5130}\) = 1.30035 = appr. 1.3.
The Beta has increased very slightly as the proportions have not changed significantly.
![]()
Question 33.
Ms. Preeti, a school teacher, after retirement has built up a portfolio of ₹ 1,20,000 which is as follows:
| Shares | No. of shares | Price per share | Beta |
| ABC Ltd. | 1000 | ₹ 50 | 0.9 |
| DEF Ltd. | 500 | ₹ 20 | 1.0 |
| GHI Ltd. | 800 | ₹ 25 | 1.5 |
| JKL Ltd. | 200 | ? ₹ 200 | 1.2 |
Her portfolio consultant Sri Vijay has advised her to bring down the beta to 0.8. You are required to compute:
(i) Present portfolio beta
(if) How much risk free investments should be brought in, to reduce the beta to 0.8. [May 2019] [8 Marks]
Answer:
(a) Portfolio Beta :
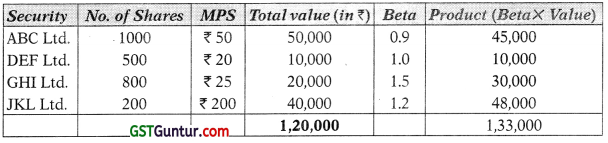
Portfolio Beta = \(\frac{1,33,000}{1,20,000}\) = 1.1083
(ii) Risk free security to be purchase for β = 0.80
| Investment | Beta | Weight | Product |
| Risk free | 0 | w | 0 |
| Portfolio | 1.1083 | 1 – w | 1.1083 – 1.1083w |
| Total | 1.1083 – 1.1083w |
Portfolio Beta = 0.80 = \(\frac{1.1083-1.1083 w}{1}\)
w = 0.2782 or 27.80% approx.
Amount to he invested in risk free securities
27.80% of ₹ 1,20,000 = ₹ 33,360.
It is assumed that no further inflow of money will occur and the amount should be arranged by selling the existing securities in the same proportion.
No. of shares to be sold
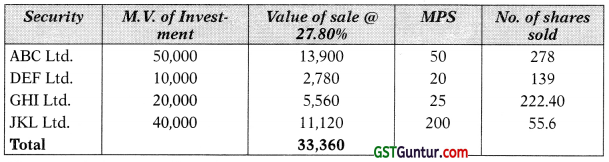
Alternate Solution to Part (ii) :
Required Beta 0.8
It should become (0.8/1.08) 72.2% of present portfolio
If Rs. 1,20,000 is 72.20%, the total portfolio should be Rs. 1,20,000 × 100/72.20 or Rs. 1,66,205
Additional investment in zero risk should be (Rs. 1,66,205 – Rs. 1,20,000) = Rs. 46,205
Revised Portfolio will he
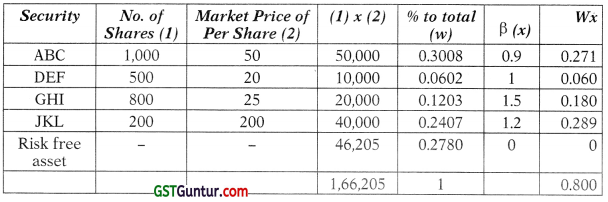
Question 34.
(a) Mr. Abhishek is interested in investing ? 2,00,000 for which he is considering following three alternatives:
(i) Invest ₹ 2,00,000 in Mutual Fund X (MFX)
(ii) Invest ₹ 2,00,000 in Mutual Fund Y (MFY)
(iii) Invest ₹ 1,20,000 in Mutual Fund X (MFX) and ₹ 80,000 in Mutual Fund Y (MFY)
Average annual return earned by MFX and MFY is 15% and 14% respectively. Risk free rate of return is 10% and market rate of return is 12%.
Covariance of returns of MFX, MFY and market portfolio Mix are as follow:
| A MFX | MFY | MIX | |
| MFX | 4.800 | 4.300 | 3.370 |
| MFY | 4.300 | 4.250 | 2.800 |
| M | 3.370 | 2.800 | 3.100 |
You are required to calculate:
(i) variance of return from MFX, MFY and market return,
(ii) portfolio return, beta, portfolio variance and portfolio standard deviation,
(in) expected return, systematic risk and unsystematic risk; and
(iv) Sharpe ratio, Treynor ratio and Alpha of MFX, MFY and Portfolio Mix. [May 2016] [Nov. 2016] [8 Marks]
Answer:
(i) Variance of Returns
Corii,j = \(\frac{{Cov}(i, j)}{\sigma_i \sigma_j}\)
Accordingly, for MFX
1 = \(\frac{{Cov}(X, X)}{\sigma_x \sigma_x}\)
σx2 = 4.800
Accordingly, for MFY
j = \(\frac{{Cov}(Y, Y)}{\sigma_y \sigma_y}\)
σy2 = 4.250
Accordingly, for Market Return
1 = \(\frac{{Cov}(M, M)}{\sigma_M \sigma_M}\)
σM2 = 3.100
(ii) Portfolio return beta, variance and standard deviation
Weight of MFX in portfolio = \(\frac{1,20,000}{2,00,000}\) = 0.60
Weight of MFY in portfolio = \(\frac{80,000}{2,00,000}\) = 0.40
Accordingly Portfolio Return
0.60 × 1596 + 0.40 × 1496 = 14.60%
Beta of each Fund
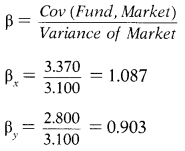
Portfolio Beta
0.60 × 1.087 + 0.40 × 0.903 = 1.013
Portfolio Variance using Markowitz Model
σxy2 = Wx2σx2 + Wy2σy2 + 2 WxWyCovx,y
= (0.60)2 (4.800) + (0.40)2 (4.250) + 2(0.60) (0.40) (4.300)
= 4.472
Or Portfolio Standard Deviation
σxy = \(\sqrt{4.472}\) = 2.115
(iii) Expected Return, Systematic and Unsystematic Risk of Portfolio
Portfolio Return = 10% + 1.0134 (12% – 10%) = 12.03%
MF X Return = 10% + 1.087 (12% – 10%) = 12.17%
MF Y Return = 10% + 0.903 (12% – 10%) = 11.81%
Systematic Risk = β2σ2
Accordingly,
Systematic Risk of MFX = (1.087)2 × 3.10 = 3.663
Systematic Risk of MFY = (0.903)2 × 3.10 = 2.528
Systematic Risk of Portfolio = (1.013)2 × 3.10= 3.181
Unsystematic Risk = Total Risk – Systematic Risk Accordingly,
Unsystematic Risk of MFX = 4.80 – 3.663 = 1.137
Unsystematic Risk of MFY = 4.250 – 2.528 = 1.722
Unsystematic Risk of Portfolio = 4.472 – 3.181 = 1.291
(iv) Sharpe and Treynor Ratios and Alpha

Alpha Actual Return – Expected
MFX = 15% – 12.17% = 2.83%
MFY = 14% – 11.81% = 2.19%
Portfolio = 14.6% – 12.03% = 2.57%
Question 35.
Ramesh wants to invest in stock market. He has got the following information about individual securities.
| Security | 1 Expected Return | Beta | σ2c. |
| A | 15 | 1.5 | 40 |
| B | 12 | 2 | 20 |
| C | 10 | 2.5 | 30 |
| D | 09 | 1 | 10 |
| E | 08 | 1.2 | 20 |
| F | 14 | 1.5 | 30 |
Market index variance is 10 per cent and the risk free rate of return is 7%. What should be the optimum portfolio assuming no short sales? [May 2010] [12 Marks]
Answer:
Securities need to be ranked on the basis of excess return to beta ratio from highest to the lowest.
Ranked Table:
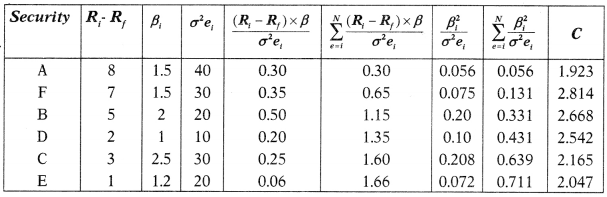
CA = 10 × 0.30/ [1 + (10 × 0.056)] = 1.923
CF = 10 × 0.65/ [1 + (10 × 0.131)] = 2.814
CB = 10 × 1.1.15 / [1 + (10 × 0.331)] = 2.668
CD = 10 × 1.35 / [1 + (10 × 0.431)] = 2.542
CC = 10 × 1.60 / [1 + (10 × 0.639)] = 2.165
CE = 10 × 1.66 / [1 + (10 × 0.7111)] = 2.047
Cut off point is 2.814
Zi = \(\frac{\beta_i}{\sigma^2 e_i}\left[\frac{R_i-R_f}{\beta_i}-c\right]\)
ZA = 15/40 (5.33 -2.814) = 0.09435
ZF = 15/30 (4.67-2.814) = 0.09435
XA = 0.09435/[0.09435 +0.0928] = 50.41%
XF = 0.0928/[0.09435 + 0.0928] = 49.59%
Funds to be invested in security A & F are 50.41% and 49.59% respectively.
![]()
Question 36.
Equity of KGF Ltd. (KGFL) is ₹ 410 Crores, its debt is worth ₹ 170 Crores. Printer Division segments Value is attributable to 74%, which has an asset Beta (βp) of 1.45, balance value is applied on spares and Consumables division, which has an Asset Beta (βsc) of 1.20. KGFL Debt beta (βn) is 0.24.
You are required to calculate:
(i) Equity Beta (βE)
(ii) Ascertain Equity Beta (βE), If KGF Ltd. decides to changes its Debt Equity Position by raising further debt and buying back of equity to have its Debt Equity Ratio at 1.90. Assume that the present Debt Beta(βD1) is 0.35 and any further funds raised by way of Debt will have a Beta (βD2) of 0.40.
(iii) Whether the new Equity Beta (βE) justifies increases in the value of equity on account of leverage? [May 2019][8 Marks]
Answer:
(i) Equity Beta of KGFL Ltd.:
Equity Beta of KGFL Ltd. will be the weighted average of the equity Beta of its two divisions. The weight of printer division (p) is 0.74 and the weight of Spares and Consumables (SC) division is 0.24. The equity debt proportion of the company is \(\frac{E}{E+D}=\frac{410}{410+170}\) = o 7069
therefore the balance is debt i.e. (1 – 0.7069) = 0.2931.
Using formula:
(βA) = βE × \(\frac{E}{E+D}\) + βD × \(\frac{D}{E+D}\)
Equity Beta of the two divisions:

Equity Beta of KGFL Ltd = 1.95(0.74) + 1.60(0.26)
= 1.443 + 0.416
= 1.859 = 1.86 approx.
(ii) If Debt equity ratio is 1.9 and equity is 1, it means the proportion of debt will be \(\) = 0.655 and equity proportion will be \(\) = 0.345. This means that debt will be to the tune of ₹ 380 (0.655 × 580) and equity will be 200 (0.345 × 580). Since the existing debt is ₹ 170 crores, the balance 210 crores (380 – 170) will be freshly raised. The new overall debt Beta will be =
βD1 × \(\frac{\mathrm{D} 1}{\mathrm{D} 1+\mathrm{D} 2}\) + βD1 × \(\frac{\mathrm{D} 2}{\mathrm{D} 1+\mathrm{D} 2}\)
= 0.35 × \(\frac{170}{380}\) + 0.40 × \(\frac{210}{380}\) = 0.3776
= 0.38 approx.
Assuming the asset Beta of the two divisions is still the same, the new equity beta of KGFL will be :

Equity Beta of KGFL Ltd = 3.48(0.74) + 2.76(0.26) = 2.575 +0.7176
= 3.292 = 3.3 approx.
(iii) Yes, it justifies the increase as it leads to increase in the value of Equity due to increase in Beta.