This Measures of Central Tendency – CA Foundation Statistics Notes is designed strictly as per the latest syllabus and exam pattern.
Measures of Central Tendency – CA Foundation Statistics Notes
Previous Year Exam Questions
Question 1.
If X and Y are related by X – Y – 10 = 0 and mode of X is known to be 23, then the mode of Y is : [1 Mark, Nov. 2006]
(a) 20
(b) 13
(c) 3
(d) 23
Solution:
(b) 13
(b) is correct
Given Relation is x – y – 10 = 0
XM0 = 23 (given)
∴ 23 – YM0 -10 = 0
∴ YM0 = 13
Question 2.
A man travels at a speed of 20 km/hr and then returns at a speed of 30 km/ hr. His average speed of the whole journey is: [1 Mark, Nov. 2006]
(a) 25 km/ hr
(b) 24.5 km/ hr
(c) 24 km/hr
(d) None
Solution:
Tricks:- Av. Speed = \(\frac{2 x y}{x+y}\)
Where x & y are speeds for same distances.
Average speed = \(\frac{2 \times 20 \times 30}{20+30}\) = 24 Km/hr.
![]()
Question 3.
The sum of the squares of deviations of a set of observations has the smallest value, when the deviations are taken from their: [1 Mark, Feb. 2007]
(a) A. M.
(b) H. M.
(c) G. M.
(d) None
Solution:
(a) A. M.
(a) is Correct.
Rule :The sum of squares of deviations from actual mean (i.e. Arithmetic mean) is Minimum.
Question 4.
Which of the following result hold for a set of distinct positive observations? [1 Mark, May 2007]
(a) A. M. ≥ G. M. ≥ H. M.
(b) GM. > A.M. > H.M.
(c) G M. > A. M. ≥ H. M.
(d) A. M. > G. M. > H. M
Solution:
(d) A. M. > G. M. > H. M
(d) For a distinct set of positive observation AM > GM > H.M. & if obs.are equal, then AM = GM = H.M.
Question 5.
If the A.M. and H.M. for two numbers are 5 and 3.2 respectively then the G.M. will be: [1 Mark, Aug. 2007]
(a) 4.05
(b) 16
(c) 4
(d) 4.10
Solution:
(c) 4
Since AM. = 5 ; HM. = 3.2
GM. = \(\sqrt{\mathrm{A} \cdot \mathrm{H}}\) = \(\sqrt{5 \times 3.2}\) = 4
Question 6.
An aeroplane flies from A to B at the rate of 500 km / hr and comes back from B to A at the rate of 700 km / hr. The average speed of the aeroplane is : [1 Mark, Nov. 2007]
(a) 600 km/hr
(b) 583.33 km/hr
(c) 100 \(\sqrt{35}\) km /hr
(d) 620 km/hr.
Solution:
(b) 583.33 km/hr
(b) TRICK
Average speed = \(\frac{2.500 .700}{500+700}\) = 583.33km/hr.
Question 7.
For a moderately skewed distribution, which of the following relationship holds? [1 Mark, Nov. 2007]
(a) Mean – Median = 3 (Median – Mode)
(b) Median -Mode = 3 (Mean -Median)
(c) Mean – Mode 3 (Mean – Median)
(d) Mean – Median 3 (Mean – Mode)
Solution:
(c) Mean – Mode 3 (Mean – Median)
For a Moderately Skewed Distribution
Empirical Relationship = Mo = 3Me – 2Mean
OR ; Mean – Mode = 3 (Mean- Median)
![]()
Question 8.
____ & ____ are called ratio averages: [1 Mark, Nov. 2007]
(a) H.M.&GM.
(b) H.M.&A.M.
(c) A. M. & G. M.
(d) None
Solution:
(a) H.M. and G.M. are used in ratio averages and percentages and it is also used in computing average rates of increase or decrease.
Question 9.
Extreme values have ____ effect on mode: [1 Mark, Feb. 2008]
(a) High
(b) low
(c) No
(d) None of these
Solution:
(c) No
Mode :- The value having occurrence the maximum number of times i. e. the maximum concentration of the observations around it. Hence, extreme values have no effect on Mode.
Question 10.
The mean salary for a group of 40 female workers is ₹ 5200 per month and that for a group of 60 male workers is ₹ 6800 per month. What is the combined salary ?
(a) ₹ 6160
(b) ₹ 6280
(c) ₹ 6890
(d) ₹ 6920
Solution:
(a) We have n1 = 40, n2 = 60
\(\overline{\mathbf{X}_1}\) = Rs 5200 and \(\overline{\mathbf{X}_2}\) = ₹ 6800
Hence, the combined mean salary per month is:
\(\overline{\mathrm{X}_{12}}\) = \(\frac{\mathrm{n}_1 \overline{\mathrm{X}_1}+\mathrm{n}_2 \overline{\mathrm{X}_2}}{\mathrm{n}_1+\mathrm{n}_2}\) = \(\frac{40 \times 5200+60 \times 6800}{40+60}\) = Rs. 6160
![]()
Question 11.
If there are two groups with 75 and 65 as harmonic means and containing 15 and 13 observations, then the combined H.M. is given by : [1 Mark, June 2008]
(a) 70
(b) 80
(c) 70.35
(d) 69.48
Solution:
(a) 70
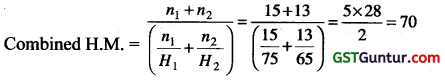
Question 12.
The G.M. of 4, 6 and 8 is :
(a) 4.77
(b) 5.32
(c) 6.14
(d) 5.77
Solution:
(d) 5.77
When a variable x assumes n values X1, X2, X3, …… Xn all being positive, then G.M. of X is given by
G = (X1.X2.X3………. Xn)1/n
G = (4×6×8)1/3 = (192)1/3 = 5.77
Tricks : Go by choices
Product of these obs. = cube of GM.
Question 13.
G.M is a better measure than others when, [1 Mark, Dec. 2008]
(a) Ratios and percentages are given
(b) Interval of scale is given
(c) Both (a) and (b)
(d) Either (a) or (b)
Solution:
(a) G.M is not used as widely as the A.M. but sometimes it is more significant than the A.M. when ratio and percentage changes are more important than the absolute changes.
Question 14.
The median of x, \(\frac{x}{2}\), \(\frac{x}{3}\), \(\frac{x}{5}\) is 10.Find x where x > 0 [1 Mark, June 2009]
(a) 24
(b) 32
(c) 8
(d) 16
Solution:
(a) 24
TRICKS : Obs. are in descending order.
No. of obs. = 4 ( Even )
M = Me = Av. of middle two terms
M = \(\frac{1}{2}\)(\(\frac{x}{2}\) + \(\frac{x}{3}\)) = 10
5x = 120
x = 24
Question 15.
The average salary of 50 men was ₹ 80 but it was found that salary of 2 of them were ₹ 46 and ₹ 28 which was wrongly taken as ₹ 64 and ₹ 82. The revised average salary is: [1 Mark, June 2009]
(a) ₹ 80
(b) ₹ 78.56
(c) ₹ 85.26
(d) ₹ 82.92
Solution:
(b) Correct Mean =
\(\frac{\sum X-64-82+46+28}{50}\)
\(\frac{50 \times 80-146+74}{50}\) = 78’56
Question 16.
If A be the A.M. of two positive unequal quantities X and Y and G be their G.M., then [1 Mark, June 2009]
(a) A < G (b) A > G
(c) A ≤ G
(d) A ≥ G
Solution:
(b) A > G
Since X ≠ Y
So A > G >H
![]()
Question 17.
When mean is 3.57 and mode is 2.13 then value of median is _____. [1 Mark, Dec. 2009]
(a) 3.09
(b) 5.01
(c) 4.01
(d) None of these
Solution:
(a) 3.09
Empirical formula,
Mode = 3 Median – 2 Mean
3 Me = Mo + 2 Mean
= 2.13 + 2 × 3.57
Me = \(\frac{9.27}{3}\) = 3.09.
Question 18.
The harmonic mean of 1, 1/2, 1/3 …….. 1/n is [1 Mark, June 2010]
(a) 1/(n + 1)
(b) 2/(n+ 1)
(c) (n + 1)/2
(d) 1/(n – 1)
Solution:
(b) 2/(n+ 1)

Tricks : GBC
Question 19.
The mean weight of 15 students is 110 kg. The mean weight of 5 of them is 100 kg. and that of another five students is 125 kg., then the mean weight of the remaining students is: [1 Mark, June 2010]
(a) 120
(b) 105
(c) 115
(d) None of these
Solution:
(b) 105
Total weight of remaining 5 students = 15 × 110 – 5 × 100 – 5 × 125 = 525
∴ Mean weight of remaining 5 students = \(\frac{525}{5}\) = 105
Question 20.
In a class of 11 students, 3 students were failed in a test. 8 students who passed secured 10,11,20,15,12,14,26 and 24 marks respectively. What will be the median marks of the students: [1 Mark, June 2010]
(a) 12
(b) 15
(c) 13
(d) 13.5
Solution:
(a) 12
Let x1, x2, x3 be the marks of fail 3 students. Arranging marks in ascending order; we get x1, x2, x3, 10, 11, 12, 14, 15, 20, 24, 26 Median = Middle obs. = 12
Question 21.
A lady travel at a speed of 20km/h and returned at quicker speed. If her average speed of the whole journey is 24km/h, find the speed of return journey (in km/h) [1 Mark, Dec. 2010]
(a) 25
(b) 30
(c) 35
(d) 38
Solution:
(b) 30
TRICKS : Av. Speed = \(\frac{2 \times 20 x}{x+20}\) = 24
Where x = Retuning Speed
24x + 480 = 40x
16x = 480
x = 30 km/hr.
Question 22.
Let the mean of the variable ‘x’ be 50, then the mean of u = 10 + 5x will be: [1 Mark, Dec. 2010]
(a) 250
(b) 260
(c) 265
(d) 273
Solution:
(b) 260
u = 10 + 5x
Since mean changes w.r.t the change of Origin & Scale
∴ New Mean of u = 10 + 5 × 50 = 260
![]()
Question 23.
If the difference between mean and mode is 63, then the difference between Mean and Median will be _____ [1 Mark, June 2011]
(a) 63
(b) 31.5
(c) 21
(d) None of the above
Solution:
(c) 21
Given : Mode – Mean = 63
Since ; Empirical Relationship is (Mode – Mean) = 3 (Median – Mean)
Median – Mean = \(\frac{63}{3}\) = 21
Question 24.
If the Arithmetic mean between two numbers is 64 and the Geometric mean between them is 16. The Harmonic Mean between them is _____. [1 Mark, June 2011]
(a) 64
(b) 4
(c) 16
(d) 40
Solution:
(b) 4
Given : A.M = A = 64
G.M. = G= 16; H.M = ?
We know, (G.M.)2 = A.M. × HM.
(16)2 = 64 × H.M.
∴ H.M. = \(\frac{256}{64}\) = 4
Question 25.
The average of 5 quantities is 6 and the average of 3 is 8. What is the average of the remaining two? [1 Mark, June 2011]
(a) 4
(b) 5
(c) 3
(d) 3.5
Solution:
(c) 3
Sum of Remaining two Nos. = 5 × 6 – 3 × 8 = 6
∴ Av. of Remaining two = \(\frac{6}{2}\) = 3
Question 26.
The median of following numbers, which are given in ascending order is 25. Find the Value of X if date is 11, 13, 15, 19, (x + 2), (x + 4), 30, 35, 39, 46 [1 Mark, Dec. 2011]
(a) 22
(b) 20
(c) 15
(d) 30
Solution:
(a) 22
Numbers are in Ascending Order ; N = 10 (Even)
Median = Av. of Middle two obs.
25 = \(\frac{1}{2}\)[(x + 2)+(x + 4)]
50 = 2x +6 ;
2x = 50 – 6
x = 22
Tricks : – GBC.
Question 27.
The average age of a group of 10 students was 20 years. The average age are increased by two years when two new students joined the group. What is the average age of two new students who joined the group ? [1 Mark, Dec. 2011]
(a) 22 years
(b) 30 years
(c) 44 years
(d) 32 years
Solution:
(d) 32 years
Sum of age of two boys = (10 + 2) × (20 + 2) – 10 × 20
= 264 – 200 = 64
Average Age of two boys = \(\frac{64}{2}\) = 32
Question 28.
Geometric Mean of three observations 40, 50 and X is 10. The value of X is [1 Mark, June 2010]
(a) 2
(b) 4
(c) 1/2
(d) None of the above
Solution:
(c) 1/2
Tricks: Product of obs. = (GM)3
(10)3 = 40.50.X
1,000 = 40.50.X
X = \(\frac{10}{20}\) = \(\frac{1}{2}\)
Question 29.
The mean of first three terms is 14 and mean of next two terms is 18. The mean of all five terms is: [1 Mark, June 2010]
(a) 14.5
(b) 15
(c) 14
(d) 15.6
Solution:
(d) 15.6
ΣX = N.\(\overline{\mathbf{X}}\)
Sum of 1 st 3 Numbers = 3 × 14 = 42
Sum of next 2 Numbers = 2 × 18 = 36
Sum of all these 5 Numbers = \(\frac{78}{5}\) = 15.6
Tricks : Combined Mean = \(\frac{3 \times 14+2 \times 18}{3+2}\) = 15.6
Question 30.
The mean salary of a group of 50 persons is ₹ 5,850. Later on it is discovered that the salary of one employee has been wrongly taken as ₹ 8,000 instead of ₹ 7,800. The corrected mean salary is [1 Mark, Dec. 2012]
(a) ₹ 5,854
(b) ₹ 5,846
(c) ₹ 5,650
(d) None of the above
Solution:
(b) ₹ 5,846

TRICKS : Do with Calculator mentally
Question 31.
If the mode of a data is 18 and mean is 24 then median is [1 Mark, Dec. 2012]
(a) 18
(b) 24
(c) 22
(d) 21
Solution:
(c) 22
Mode = 18; Mean = 24
Mode = 3 Median – 2 Mean
18 = 3 Median – 2 × 24
18 = 3 Median – 48
18 + 48 = 3 Median
Median = \(\frac{66}{3}\) = 22
![]()
Question 32.
For data on frequency distribution of weights : [1 Mark, Dec. 2012]
70, 73, 49, 57, 56, 44, 56, 71, 65, 62, 60, 50, 55, 49, 63 and 45
If we assume class length as 5, the number of class intervals would be (a) 5 (b) 6 (c) 7 (d) 8
(a) 5
(b) 6
(c) 7
(d) 8
Solution:
(b) 6
L = Largest obs. = 73
S = Smallest obs. = 44
Range = L – S = 73 – 44 = 29
Length = i = 5
No. of Class – Intervals \(=\frac{\text { Range }}{\mathrm{i}}\) = \(\frac{29}{5}\) = 5.8 = 6
Question 33.
The point of intersection of the “less then” and “more then” Ogives correspond to [1 Mark, Dec. 2012]
(a) Mean
(b) Mode
(c) Median
(d) 10th percentile
Solution:
(c) Median
Question 34.
A man travels from Agra to Gwalior at an average speed of 30 km per hour and back at an average speed of 60 km per hour. What is his average speed? [1 Mark, Dec. 2012]
(a) 38 km per hour
(b) 40 km per hour
(c) 45 km per hour
(d) 35 km per hour
Solution:
(b) 40 km per hour
Given x = 30 km/h & y = 60 km/h
Average speed = \(\frac{2 \times 30 \times 60}{30+60}\)
= \(\frac{2 \times 30 \times 60}{90}\) = 40 km per hour
Question 35.
Which of the following measures of central tendency cannot be shown by graphical method? [1 Mark, June 2013]
(a) Mean
(b) Median
(c) Mode
(d) Quartiles
Solution:
(a) Mean
Mean Cannot be Shown with Graphical Method.
Question 36.
GM of 8, 4, 2 is ____
(a) 4
(b) 2
(c) 8
(d) None
Solution:
(a) 4
4 is correct
G = (8.4.2)1/3 = (23.22.2)1/3
= (26)1/3 = 22 = 4
Tricks : Go by choices
![]()
Question 37.
The average age of 15 students is 15 years. Out of these the average age of 5 students is 14 years and that of other 9 students is 16 years, then the age of 15th student is _____ [1 Mark, June 2013]
(a) 11 years
(b) 14 years
(c) 15 years
(d) None of these
Solution:
(a) 11 years
(a) is correct
Age of 15th student = 15 × 15 – 5 × 14 – 9 × 16 = 11 years
Question 38.
Which of the following statement is true? [1 Mark, June 2014]
(a) Median is based on all observations
(b) The Mode is the mid value
(c) The Median is the 2nd Quartile
(d) The Mode is the 5th decile
Solution:
(c) The Median is the 2nd Quartile
(c) is correct
Median M = Q2
Question 39.
For two numbers A.M. = 10 and G.M. = 8; the H.M …..? [1 Mark, Dec. 2014]
(a) 9
(b) 8.9
(c) 6.4
(d) None
Solution:
(c) 6.4
(c) is correct
∵ AH = G2 ⇒ H = \(\frac{G^2}{\mathrm{~A}}\)
H = \(\frac{8^2}{10}\) = 6.4
Question 40.
The 3rd decile for the values 15,10,20, 25, 18,11, 9, 12 is [1 Mark, Dec. 2014]
(a) 13
(b) 10.7
(c) 11
(d) 11.5
Solution:
(b) 10.7
(b) is correct
Arranging in Ascending order
9, 10, 11, 12, 15, 18, 20, 25
N = 8
∴ D3 = 3\(\left(\frac{N+1}{10}\right)^{\text {th }}\) obs. = 3\(\left(\frac{8+1}{10}\right)\) = 2.7th obs.
= 2nd obs. + 0.7(3rd – 2ndobs.)
= 10 + 0.7(11 – 10)
= 10.7
Question 41.
The A.M. of square of first ‘2n’ natural number is [1 Mark, Dec. 2014]
(a) \(\frac{1}{6}\)(2n + 1)(4n – 1)
(b) \(\frac{1}{6}\)(2n – 1)(4n – 1)
(c) \(\frac{1}{6}\)(2n – 1)(4n + 1)
(d) \(\frac{1}{6}\)(2n + 1)(4n + 1)
Solution:
(d) \(\frac{1}{6}\)(2n + 1)(4n + 1)
(d) is correct

Tricks: GBC
Question 42.
A Random variables x follows uniform distribution in the interval [-3, 7].Then the mean of distribution is [1 Mark, Dec. 2014]
(a) 2
(b) 4
(c) 5
(d) 6
Solution:
(a) 2
(a) is correct
Note:- Random variable has uniform distribution i.e.
Here, Arithemetic Mean is applied
∴ Mean = \(\frac{-3+7}{2}\) = 2
Question 43.
If the Harmonic mean of two numbers is 4 and Arithmetic mean (A) and Geometric mean (G) satisfy the equation 2A + G = 27 then the two numbers are [1 Mark, June 2015]
(a) (1, 3)
(b) (9, 5)
(c) (6, 3)
(d) (12, 7)
Solution:
(c) (6, 3)
Tricks : (a) Go by choices
For option (c) ; H = \(\frac{2 a b}{a+b}\) = \(\frac{2 \times 6 \times 3}{6+3}\) = H(true)
A = \(\frac{6+3}{2}\) = 4.5
G = \(\sqrt{a b}\) = \(\sqrt{6 \times 3}\) = \(\sqrt{18}\)
It satisfies 2A + G2 = 27
∴ (c) is correct
Question 44.
There were 50 students in a class. 10 failed whose average marks were 2.5. The total marks of class were 281. Find the average marks of students who passed? [1 Mark, Dec. 2015]
(a) 6.4
(b) 25
(c) 256
(d) 86
Solution:
(a) 6.4
(a) is correct.
Average Marks of students who passed = \(\frac{281-10 \times 2.5}{50-10}\) = 6.4
Question 45.
If the mean of two numbers is 30 and Geometric Mean is 24 then what will be those two numbers ? [1 Mark, June 2016]
(a) 36 and 24
(b) 30 and 30
(c) 48 and 12
(d) None of these
Solution:
(d) None of these
(c) is correct.
Tricks: Go by choices
(c) Arithmetic Mean = \(\frac{48+12}{2}\) = 30
Geometric Mean = \(\sqrt{48 \times 12}\) = 24
It satisfies all conditions.
![]()
Question 46.
The G.M. of observations 40, 50 and x is 10, then find the value of x ? [1 Mark, Dec. 2016]
(a) 4
(b) 5
(c) 2
(d) \(\frac{1}{2}\)
Solution:
(d) \(\frac{1}{2}\)
(D) is correct.
Tricks : Product of observations = (GM) No. of obs.
40 × 50 × x = 103
So, x = \(\frac{1}{2}\)
Question 47.
If the mean of data is 55.6 and the mode is 46, then the median is [1 Mark, Dec. 2016]
(a) 50.4
(b) 40.7
(c) 52.4
(d) None
Solution:
(c) 52.4
(c) is correct.
Since, Mode = 3Median – 2 Mean
46 = 3Median – 2 × 55.6
So, Median = (46 + 111.2)/3 = 52.4
Question 48.
_____ is used for ordering the size of designed cloths. [1 Mark, Dec. 2016]
(a) Mean
(b) Median
(c) Mode
(d) None
Solution:
(c) Mode
(c) is correct.
Question 49.
The mean of 10 observations is 14.4. Out of these mean of 4 observations is 16.5, then find the mean of remaining observations? [1 Mark, Dec. 2016]
(a) 13.6
(b) 13
(c) 13.8
(d) 12
Solution:
(b) 13
(b) is correct.
No. of remaining observations = 10 – 4 = 6
Sum of these 6 observations = 14.4 × 10 – 4 × 16.5 = 78
Their mean = 78/6 = 13
Question 50.
The mean of 6, 4, 1, 5, 6, 10 and 3 is 5. If each number is added with 2, then the new mean is _____ [1 Mark, Dec. 2016]
(a) 7
(b) 5
(c) 6
(d) 10
Solution:
(a) 7
(a) is correct.
Question 51.
Which of the following is correct ? [1 Mark, June 2017]
(a) 3 (Mean – Median) = Mean – Mode
(b) Mean – Median = 3(Mean – Mode)
(c) Mean – Median = 2(Mean – Mode)
(d) Mean – Mode = 2(Mean – Median)
Solution:
(a) 3 (Mean – Median) = Mean – Mode
(a) is correct
Question 52.
A person purchases 5 rupees worth of eggs from 10 different markets. You are to find average No. of eggs per rupee for all the markets taken together. What is the suitable form of average in this case? [1 Mark, June 2017]
(a) AM
(b) GM
(c) HM
(d) None
Solution:
(c) HM
(c) is correct.
Question 53.
GM = 6, AM = 6.5 then HM = [1 Mark, June 2017]
(a) \(\frac{6^2}{6.5}\)
(b) \(\frac{6}{6.5}\)
(c) \(\frac{6.5}{6}\)
(d) None
Solution:
(a) \(\frac{6^2}{6.5}\)
Formula ; G2 = A.H.
⇒ 62 = (6.5)H.
or H = \(\frac{6^2}{6.5}\)
∴ (a) is correct.
Question 54.
A company’s past 10 years average earnings was ₹40 crores. For obtaining the same average earnings for 11 years including these 10 years how much earning (in ₹) must be made by the company in the 11th year ? [1 Mark, June 2017]
(a) 40 crores
(b) \(\frac{40 \times 10}{11}\) crores
(c) More than 40 crores
(d) None
Solution:
Earning in 11th year = 11 × 40 – 10 × 40 = ₹ 40 crores
(a) is correct.
![]()
Question 55.
The rates of returns from three different shares are 100%, 200% and 400% respectively, the average rate of return will be [1 Mark, June 2017]
(a) 350%
(b) 233.33%
(c) 200%
(d) 300%
Solution:
(c) 200%
Gm = (100 × 200 × 400)1/3
= 200%
Question 56.
Mean of 7, 9, 12, x, 4, 11 & 5 is 9. Find the missing observation : [1 Mark, Dec. 2017]
(a) 13
(b) 15
(c) 12
(d) None of these
Solution:
(b) 15
x = 7 × 9 – 7 – 9 – 12 – 4 – 11 – 5
= 15.
Question 57.
If all the frequencies are equal then which will doesn’t exist: [1 Mark, Dec. 2017]
(a) Mean
(b) Median
(c) Mode
(d) None of these
Solution:
(c) Mode
Question 58.
_____ is the reciprocal of the AM of reciprocal of observation : [1 Mark, Dec. 2017]
(a) HM
(b) GM
(c) Both
(d) None of these
Solution:
(a) HM
Question 59.
Mean of n observation is \(\bar{x}\), if first observation is increased by 1, 2nd observation is by 2 and so on, then new mean is _____ [1 Mark, June 2018]
(a) \(\bar{x}\) + n.n
(b) \(\bar{x}\) + \(\frac{\mathrm{n}+1}{2}\)
(c) \(\bar{x}\) + \(\frac{\mathbf{n}}{2}\)
(d) \(\bar{x}\) + n [1 Mark, June 2018]
Solution:
(b) \(\bar{x}\) + \(\frac{\mathrm{n}+1}{2}\)
New Mean = \(\frac{n \bar{x}+(1+2+3+\ldots \ldots+n)}{n}\)
= \(\overline{\mathrm{X}}\) + \(\frac{n(n+1)}{2 n}\) = \(\overline{\mathbf{X}}\) + \(\frac{(n+1)}{2}\)
Question 60.
G.M. of 4, 8, 16, 32 and 64 is _____ [1 Mark, June 2018]
(a) 8
(b) 16
(c) 32
(d) 64
Solution:
(b) 16
Tricks : 4, 8,16, 32, 64 are in G.P.
∴ GM = Middle observation = 16.
Question 61.
Which of the following results hold for a set of distinct positive observations? [1 Mark, June 2018]
(a) AM ≥ GM ≥ HM
(b) HM ≥ GM ≥ AM
(c) AM > GM > HM
(d) GM > AM > HM
Solution:
(c) AM > GM > HM
Question 62.
For a moderately skewed distribution, which of the following relationship holds? [1 Mark, June 2018]
(a) Mean – Mode = 3 (Mean – Median)
(b) Median – Mode = 3 (Mean – Median)
(c) Mean – Median = 3 (Mean – Mode)
(d) Mean – Median = 3 (Median – Mode)
Solution:
(a) Mean – Mode = 3 (Mean – Median)
![]()
Question 63.
If the variables X and Z are so related that Z = aX + b for each X = x1, where a and b are constant, then \(\overline{\mathbf{Z}}\) = a\(\overline{\mathbf{X}}\) + b [1 Mark, May 2018]
(a) True
(b) False
(c) Both
(d) None
Solution:
(a) True
Question 64.
Relation between mean, median and mode is [1 Mark, May 2018]
(a) Mean – mode = 2 (mean – median)
(b) mean – median = 3 (mean – mode)
(c) mean – median = 2 (mean – mode)
(d) mean – mode = 3 (mean – median)
Solution:
(d) mean – mode = 3 (mean – median)
Question 65.
If each item is reduced by 15, A.M is [1 Mark, May 2018]
(a) reduced by 15
(b) Increased by 15
(c) reduced by 10
(d) None
Solution:
(a) reduced by 15
If each observation is reduced by 15 then new A.M. also reduced by 15, because A.M. changes with the shifting of origin.
Question 66.
For 889, 999, 391, 384, 390,480,485, 760, 111,240 Rank of median is [1 Mark, May 2018]
(a) 2.75
(b) 5.5
(c) 8.25
(d) None
Solution:
(b) 5.5
Here No. of observation (N) = 10
Rank of median (me) = \(\left(\frac{N+1}{2}\right)^{\text {th }}\) observation
= \(\left(\frac{10+1}{2}\right)^{\text {th }}\) term = 5.5th term
Rank of median (me) = 5.5
Question 67.
The average of a series of overlapping averages, each of which is based on a certain number of item within a series is known as [1 Mark, May 2018]
(a) Moving average
(b) Weighted average
(c) Simple average
(d) None
Solution:
(a) Moving average
Question 68.
If the mean of the following distribution is 6 then the value of P is [1 Mark, Nov. 2018]
| X | 2 | 4 | 6 | 10 | P + 5 |
| f: | 3 | 2 | 3 | 1 | 2 |
(a) 1
(b) 5
(c) 11
(d) 8
Solution:
(a) 1
Tricks : Go by choices
Use Calculator
(a) If P = 7 ⇒ P + 5 = 7 + 5 = 12
So; mean = press 2 × 3 = ;4 × 2 = ;6 × 3 = ; 10 × 1 = ; 12 × 2 = button, then GT button ÷11 = button 6 (True)
So, (a) is correct.
![]()
Question 69.
If total frequencies of three series are 50,60 and 90 and their means are 12,15 and 20 respectively, then the mean of their composite series is [1 Mark, Nov. 2018]
(a) 15.5
(b) 16
(c) 14.5
(d) 16.5
Solution:
(d) 16.5
Calculator Tricks:-
X123 = press 50 × 12 = ; 60 × 15 = ; 90 × 20 = button, then GT button, then ÷ (50 + 60 + 90 = 200) button
= 16.5
Question 70.
If in a moderately skewed distribution the values of mode and mean are 32.1 and 35.4 respectively, then the value of the median is [1 Mark, Nov. 2018]
(a) 33.3
(b) 34
(c) 34.3
(d) 33
Solution:
(c) 34.3
M0 = 3M – 2\(\bar{X}\)
or 32.1 = 3M – 2 × 35.4
or M = \(\frac{32.1+70.8}{3}\) = 34.3
Question 71.
The median of the data 5, 6, 7, 7, 8, 9, 10, 11, 11, 12, 15, 18, 18 and 19 is [1 Mark, Nov. 2018]
(a) 10
(b) 10.5
(c) 11.5
(d) 11
Solution:
(b) 10.5
Me = Average of middle two observations , if N = even No. of obs.
Me = \(\frac{10+11}{2}\) = 10.5
Question 72.
The means of 20 items of a data is 5 and if each item is multiplied by 3, then the new mean will be
(a) 20
(b) 5
(c) 15
(d) 10
Solution:
(c) 15
New Mean = 5 × 3 = 15
Question 73.
The Geometric mean of 3, 6, 24 and 48 is [1 Mark, Nov. 2018]
(a) 6
(b) 8
(c) 12
(d) 24
Solution:
(c) 12
GM = \(\sqrt[4]{3 \times 6 \times 24 \times 48}\) = 12
Question 74.
The Algebraic sum of the deviation of a set of values from their arithmetic mean is [1 Mark, Nov. 2018]
(a) >0
(b) =0
(c) <0
(d) None
Solution:
(b) =0
Question 75.
Which one of the following is not a central tendency ? [1 Mark, Nov. 2018]
(a) Mean Deviation
(b) Arithmetic mean
(c) Median
(d) Mode
Solution:
(a) Mean Deviation
Question 76.
The AM of 15 Observations is 9 and the AM of first 9 Observation is 11 and then AM of remaining Observation is [1 Mark, June 2019]
(a) 11
(b) 6
(c) 5
(d) 9
Solution:
(b) 6
Sum of remaining 6 observations = Sum of 15 observations – Sum of 9 observations
= 9 × 15 – 11 × 9 = 135 – 99 = 36
Average of 6 observations = \(\frac{36}{6}\) = 6
Question 77.
In a moderately Skewed distribution the values of mean & median are 12 & 8 respectively. The value of mode is [1 Mark, June 2019]
(a) 0
(b) 12
(c) 15
(d) 30
Solution:
(a) 0
Mode = 3 Median – 2 Mean
= 3 × 8 – 2 × 12 = 24 – 24 = 0
Question 78.
Which of the following is positional average ? [1 Mark, June 2019]
(a) Median
(b) GM
(c) HM
(d) AM
Solution:
(a) Median
![]()
Question 79.
For a symmetric distribution [1 Mark, June 2019]
(a) Mean = Median = Mode
(b) Mode = 3 Median – 2 Mean
(c) Mode = \(\frac{1}{3}\) Median = \(\frac{1}{2}\) Mean
(d) None
Solution:
(a) Mean = Median = Mode
For a symmetric distribution Mean = Median = Mode
Question 80.
For the distribution
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| F | 6 | 9 | 10 | 14 | 12 | 8 |
The value of median is [1 Mark, June 2019]
(a) 3.5
(b) 3
(c) 4
(d) 5
Solution:
(c) 4
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| F | 6 | 9 | 10 | 14 | 12 | 8 |
| C.F. | 6 | 15 | 25 | 39 | 51 | 59 |
N = 59
Median (Me) = The observation having cumulative frequency just equal to or just greater than \(\left(\frac{\mathrm{N}+1}{2}\right)^{\text {th }}\) term = \(\left(\frac{59+1}{2}\right)^{\mathrm{th}}\) term
= 30th term = 4