Logarithms – CA Foundation Maths Study Material

This Logarithms – CA Foundation Maths Study Material is designed strictly as per the latest syllabus and exam pattern.

Logarithms – CA Foundation Maths Study Material

[Note : See You tube “Kailash Thakur” for better understanding]
If ab = c Where a ≠ 1 and a; c > o (positive)
Then b is said to be the logarithm of the number c to the base “a” and expressed as
Log_ac = b; Where a ≠ 1.

Types of Logarithm
(i) Natural Logarithm:
The Logarithm of a number to base “e” is called Natural Logarithm.
i.e. Log_ex
where x = a number
e = 2.7183

(ii) Common Logarithm:
Logarithm of a number to the base 10 is called common Logarithm.
i.e. Log₁₀x
where x = A number
Note: If base is not given then in arithmetical or commercial work; base is always taken as 10.

Remember Some Formulae

• If a^b = c ⇔ Log_ac = b; Where a ≠ 1.
• a^xlog_ab = b^x
• log_a a = 1
• log_a 1 = 0
• log_b a = \frac{1}{\log _a b} ⇒ log_a a.log_a b = 1
• log_a a = log_a xlog_x a =log_x alog_bx
• log_b a = log_x a.log_y xlog_z y….log_b k
• log_ba = log_bx. log_x y.log _y z…. log_k a
• log_ba = \(\frac{\log _x a}{\log _x b}\)
• log_ba = \(\frac{\log _b x}{\log _a x}\)
• If log_ba = x Then
  • log_{\(\frac{1}{b}\)}a = -x
  • log_b\(\frac{1}{a}\) = -x
  • log_{\(\frac{1}{b}\)}\(\frac{1}{a}\) = +x
• log_a(mn) = log_am + log_an
• log_a(mnr….) = log_am + log_an + log_ar + ……….
• log_a\(\left(\frac{m}{n}\right)\) = log_am – log_an
• (i) log_ab(mⁿ) = log_am
• log a = n log_am.
• log_{\(\frac{1}{b}\)} m = \(\frac{n}{b}\)log_am
• If log_am = log_bm ⇒ a = b
• If log_am = log_an ⇒ m = n

Previous Year Exam Questions

Question 1.
7log\(\left(\frac{16}{15}\right)\) + 5log\(\left(\frac{25}{24}\right)\) + 3log\(\left(\frac{81}{80}\right)\) is equal to
(a) 0
(b) 1
(c) log 2
(d) log 3
Answer:

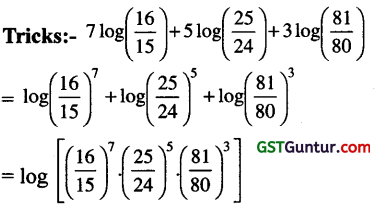
Calculation Tricks
I Type i6 ÷ 15 × button Then push = button 6 time then push M+ button.
II Type 25 ÷ 24 × button Then push = button 4 times
III Then Push × button Then MRC button 2 time Then Push M+ button
IV Type 81 ÷ 80 × button Then = button 2 times
V Then Push × button and Then MRC button 2 times Then = button
We get; it is approx 2
So. Value = log 2
(c) is Correct

Question 2.
The value of the expression a^{log_ab.log_bc.log_cd.log_dt}. [1 Mark, Feb. 2007]
(a) t
(b) abcdt
(c) (a + b + c + d + t)
(d) None.
Answer:
a^{log_ab.log_bc.log_cd.log_dt}
= a^1log_at = t¹ = t
(a) is correct

Question 3.
If log₁₀₀₀₀x = \(\frac{-1}{4}\), then x is given by: [1 Mark, Feb. 2007]
(a) 1/100
(b) 1/10
(c) 1/20
(d) None of these
Answer:
log₁₀₀₀₀x = \(\frac{-1}{4}\)
∴ (10000)^{\(\frac{-1}{4}\)} = x
or (10⁴)^{\(\frac{-1}{4}\)} = x
or x = 10^-1 = \(\frac{1}{10}\)
(b) is correct

Question 4.
If log (2a – 3b) = log a – log b, then a = ? [1 Mark, May 2007]
(a) \(\frac{3 b^2}{2 b-1}\)
(b) \(\frac{3 b}{2 b-1}\)
(c) \(\frac{b^2}{2 b+1}\)
(d) \(\frac{3 b^2}{2 b+1}\)
Answer:
log(2a – 3b) = log\(\frac{a}{b}\)
or 2a – 3b = a
or 2ab – 3b² =a
or 2ab – a = 3b²
or a(2b – 1) = 3b²
or a = \(\frac{3 b^2}{2 b-1}\)
(a) is correct

Question 5.
\(\frac{1}{\log _{a b}(a b c)}+\frac{1}{\log _{b c}(a b c)}+\frac{1}{\log _{c a}(a b c)}\) is equal to: [1 Mark, Aug. 2007]
(a) 0
(b) 1
(c) 2
(d) -1
Answer:
\(\frac{1}{\log _{a b}(a b c)}+\frac{1}{\log _{b c}(a b c)}+\frac{1}{\log _{c a}(a b c)}\)
= log_abc (abJ)c.ca) = log_abc (abc)2
= 2 log_abc (abc) = 2 × 1 = 2
∴ (c) is correct

Question 6.
Number of digits in the numeral for 2⁶⁴ [Given log 2 = 0.30103] : [1 Mark, Aug. 2007]
(a) 18 digits
(b) 19 digits
(c) 20 digits
(d) 21 digits
Answer:
(c) Let x = 2⁶⁴
log x= 64 log 2
= 64 × 0.30103
= 19.26592
x = AL (19.26592) characteristics = 19
∴ No. of digits in the number = 19 + 1 = 20
∴ (c) is correct

Question 7.
The value \(\frac{\log _3 8}{\log _9 16 . \log _4 10}\) is: [1 Mark, Nov. 2007]
(a) 3log₁₀2
(b) 7log₁₀3
(c) 3log_ez
(d) None
Answer:

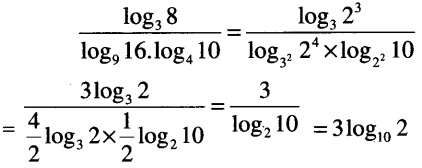
(a) is correct

Question 8.
If x = \(\) then the value of n is: [1 Mark, Feb. 2008]
(a) \(\frac{1}{2}\)log_e\(\frac{1+x}{1-x}\)
(b) log_e\(\frac{1+x}{1-x}\)
(c) log_e\(\frac{1-x}{1+x}\)
(d) log_e\(\frac{1-x}{1+x}\)
Answer:

Question 9.
log 144 is equal to:
(a) 2 log 4 + 2 log 2
(b) 4 log 2 + 2 log 3
(c) 3 log 2 + 4 log 3
(d) 3 log 2 -4 log 3
Answer:
log 144 = log(16 × 9)
= log 16 + log 9
= log 2⁴ +log 3²
= 4 log 2 + 2 log 3
(b) is correct
Tricks:- Go by choices.

Question 10.
If log₂ [log₃(log₂ x)] = 1, then x equals ; [1 Mark, June 2008]
(a) 128
(b) 256
(c) 512
(d) None
Answer:
log₂[log₃(log₂x)] = 1
Tricks:- 2³²¹ = x
or x = 2³²¹ = 2^3×3 = 2⁹ = 512
(c) is correct

Detail Method log₂ [log₃ (log₂ x)] = 1
or log₃ (log₂ x) = 2¹ = 2
or log₂x = 3²
or log₂ x = 9
or x = 2⁹ = 512
(c) is correct

Question 11.
If log\(\left(\frac{a+b}{4}\right)=\frac{1}{2}\) (log a + log b) then: \(\frac{a}{b}+\frac{b}{a}\)
(a) 12
(b) 14
(c) 16
(d) 8
Answer:
log\(\left(\frac{a+b}{4}\right)=\frac{1}{2}\) (log a + log b)
or log\(\left(\frac{a+b}{4}\right)\) = log(ab)^1/2
or \(\frac{a+b}{4}=\sqrt{a b}\)
or a + b = 4\(\sqrt{a b}\)
Squaring on both sides; we get (a + b)² = 16ab
or a² + b² + 2ab = 16ab
or a² + b² = 14ab
or \(\frac{a^2}{a b}+\frac{b^2}{a b}=\frac{14 a b}{a b}\) [Dividing by ab on both sides]
or \(\frac{a}{b}+\frac{b}{a}\) = 14
(b) is correct

Question 12.
log (m+n) = log m+ log n, m can be expressed as : [1 Mark, June 2009]
(a) m = \(\frac{n}{n-1}\)
(b) m = \(\frac{n}{n+1}\)
(c) m = \(\frac{n+1}{n}\)
(d) m = \(\frac{n+1}{n-1}\)
Answer:
log(m + n) = log m + log n
or log (m + n) = log(mn)
or m + n = mn
or m – mn = -n
or m (1 – n) = -n
or m = \(\frac{-n}{1-n}=\frac{n}{n-1}\)
∴ (a) is correct
Tricks Go by choices.

Question 13.
log₄(x² + x) – log₄(x + 1) = 2. find x. [1 Mark, June 2009]
(a) 16
(b) 0
(c) -1
(d) None of these
Answer:
log₄(x² + x) – log₄(x + 1) = 2
or log \(\left(\frac{x^2+x}{x+1}\right)\) = 2
or \(\frac{x(x+1)}{x+1}\) = 4²
or x= 16
∴ (a) is correct
Tricks: Go by choices.

Question 14.
Find the value of [log₁₀ \(\sqrt{25}\) – log₁₀(2³) + log₁₀(4)²]^x: [1 Mark, Dec. 2009]
(a) x
(b) 10
(c) 1
(d) none
Answer:
[log₁₀ \(\sqrt{25}\) – log₁₀(2³) + log₁₀(4)²]^x = [log₁₀(\(\frac{5}{8}\) × 16)]^x
= (log₁₀10)^x = 1^x = 1
∴ (c) is correct

Question 15.
If log_a b + log_a c = 0 then: [1 Mark, June 2010]
(a) b = c
(b) b = -c
(c) b = c = 1
(d) b and c are reciprocals.
Answer:
log_ab + log_ac = 0
or log_a(bc) = log_a1
∴ bc = 1
b = \(\frac{1}{c}\)
∴ (d) is correct

Question 16.
The value of 2log x + 2 log x² + 2 log x³ + ………. + 2 log xⁿ will be: [1 Mark, Dec. 2010]
(a) \(\frac{n(n+1) \log x}{2}\)
(b) n(n + 1)log x
(c) n² log x
(d) None of these
Answer:
Detail Method:
2 log x + 2 log x² + 2logx³ + ………….. + 2 log xⁿ
=2 log x + 2.2 logx + 2.3logx + ……….. + 2.n.logx
= 2 logx. [1 + 2 + 3 + ………. + n]
= 2 log x. \(\frac{n(n+1)}{2}\) = n(n+1)
= (b) is correct

Tricks Put n = 2 in options directly.
This should be equal to sum of 1st 2 terms = 2 logx + 2.2logx = 6 logx
Which gives option (b)
∴ (b) is correct.

Question 17.
Solve: \(\frac{\log _x 10-3}{2}+\frac{11-\log _x 10}{3}\) = 2. [1 Mark, Dec. 2010, June 2011]
(a) 10^-1
(b) 10²
(c) 10
(d) 10³
Answer:
\(\frac{\log _x 10-3}{2}+\frac{11-\log _x 10}{3}\) = 2
Tricks: Go by choice [Do Mentally]
For (a) x = 10^-1
L.H.S = \(\frac{\log _{\left(10^{-1}\right)} 10-3}{2}+\frac{11-\log _{10^{-1}} 10}{3}\)
= \(\frac{\log _{\left(10^{-1}\right)} 10-3}{2}+\frac{11-\log _{10^{-1}} 10}{3}\)
= -2 + 4 = 2 = (R.H.S)
∴ (a) is correct

Question 18.
If n = m! where (‘m’ is a positive integer > 2) then the value of ∴ \(\frac{1}{\log _2 n}+\frac{1}{\log _3 n}+\frac{1}{\log _4 n}+\ldots \ldots \ldots \ldots+\frac{1}{\log _m n}\). [1 Mark, June 2011]
(a) 1
(b) 0
(c) -1
(d) 2
Answer:
Given n = m !
\(\frac{1}{\log _2 n}+\frac{1}{\log _3 n}+\frac{1}{\log _4 n}+\ldots \ldots \ldots \ldots+\frac{1}{\log _m n}\)
= log_n2 + log_n3 + log_n4 + ………… + log_nm
= log_n(2. 3.4 ……………….. m)
= log_n (1 . 2. 3. 4 …………….. m) = log(ml) (ml) = 1
∴ (a) is correct

Question 19.
If log₂x + log₄x = 6, then the value of x is: [1 Mark, 2011 Dec.]
(a) 16
(b) 32
(c) 64
(d) 128
Answer:
(a) is correct
Tricks: Go by choices for (a) if x = 16
L.H.S = log₂16 + log₄ 16 = 4 + 2 = 6(R.H.S)
∴ (a) is correct

Detail Method log₂x + log₄x = 6
or log₂x + log₂2 x = 6
or log₂x + \(\frac{1}{2}\)log₂x = 6
or (1 + \(\frac{1}{2}\))log₂x = 16
or log₂x = \(\frac{6 \times 2}{3}\) = 4
∴ x = 2⁴ = 16

Question 20.
If log_xY= 100 and log₂ x = 10, then the value of‘Y’
(a) 2¹⁰
(b) 2¹⁰⁰
(c) 2^1,000
(d) 2^10,000
Answer:
(c) log 2 x = 10 ∴ x = 210
Now logxy = 100 y = ;
c100 y = (210)100 =21000 (c) is correct

Question 21.
Which of the following is true. If \(\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}=\frac{1}{a b c}\). [1 Mark, Dec.2012]
(a) log (ab + bc +ca) =abc
(b) log \(\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\) =abc
(c) log (abc) = 0
(d) log(a+b + c) = 0
Answer:
(a) is correct \(\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}=\frac{1}{a b c}\)
Multiplying both sides by abc; \(\frac{a b c}{a b}+\frac{a b c}{b c}+\frac{a b c}{c a}=\frac{a b c}{a b c}\)
or; c + a + b = 1
or; a + b + c= 1
Taking log on both sides ; we get
log (a + b + c) = log 1 = 0

Question 22.
If (log_\(\sqrt{x}\) 2)² = log_x 2 then x = [1 Mark, June 2013]
(a) 16
(b) 32
(c) 8
(d) 4
Answer:
(a) is correct (log_\(\sqrt{x}\) 2)² = log_x2
or (log_x^1/2 2)² = log_x 2
or (\(\frac{1}{\frac{1}{2}}\)log_x2)² = log_x2
or 4(log_x2)² – log_x2 = 0
or 4(log_x2)2 – log_x2 = 0
or log_x2[4log_x – 1] = 0
If log_x2 = 0 (Invalid) 4log_x2 – 1 = 0
or 4log_x2 = 1
or log_x2 = \(\frac{1}{4}\)
or x^1/4 = 2 ⇒ x = 2⁴ = 16

Tricks Go by choices
For (a) LHS = (log^ 2)² = (log4 2)²
RHS = log₁₆ 2 = log_2⁴ 2 = \(\frac{1}{4}\)log₂2 = \(\frac{1}{4}\)
(a) is correct
Note Never write; check mentally.

Question 23.
Find Value of [log_yx.log_zy.log_x z]³ =
(a) 0
(b) -1
(c) 1
(d) 3
Answer:
(c) is correct [log_yx.log_zy.log_x z]³
= [log_xx] = [1]³ = 1

Question 24.
Find the value of Log₄9.Log₃2 = [1 Mark, Dec. 2013]
(a) 3
(b) 9
(c) 2
(d) 1
Answer:
(d) is correct Log₄9.Log₃2 = l0g_(2)² (3²).log₃2
= \(\frac{2}{2}\)log₂3.log₃2
= 1 × 1 = 1

Question 25.
If X = log₂₄12; y = log₃₆ 24; z = log₄₈ 36 then xyz + 1 = ? [1 Mark, June 2014]
(a) 2xy
(b) 2zx
(c) 2yz
(d) 2
Answer:
(c) is correct xyz + 1 = log₂₄12. log₃₆ 24. log₄₈ 36+1
= log₄₈12 + log₄₈ 48
= log₄₈ (12 × 48)
= log₄₈(12 × 2)²
= 2log₄₈ 24
= 2 log₃₆ 24. log₄₈ 36
= 2yz

Question 26.
If x2 + y2 = 7xy then log \(\frac{1}{3}\)(x + y) = [1 Mark, June 2014]
(a) log x + log y
(b) \(\frac{1}{2}\)(log x + log y)
(c) \(\frac{1}{3}\)(log x + log y)
(d) \(\frac{1}{3}\)(log x. log y)
Answer:

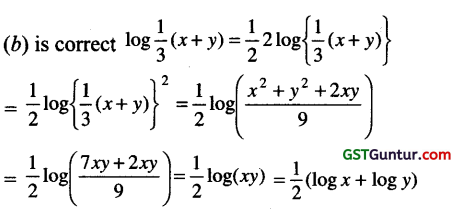
Question 27.
If log x= a – b; log y = a + b then log\(\left(\frac{10 x}{y^2}\right)\)
(a) 1- a – 3b
(b) a – 1 + 3b
(c) a + 3b – 1
(d) 1 – b + 3a
Answer:
(a) is correct
log x = a+b ; log y = a-b.
log\(\left(\frac{10 x}{y^2}\right)\) = log₁₀10 + log x – log y²
= 1 + a + b – 2log y = 1 + a + b – 2 (a – b)
= 1 + a + b – 2a + 2b = 1 – a + 3b

Question 28.
If x = 1 + log_p qr, y = 1 + log_q rp and z = 1 + log_r pq ; then the value of \(\frac{1}{\mathrm{x}}+\frac{1}{\mathrm{y}}+\frac{1}{\mathrm{z}}\) = ……….
(a) 0
(b) 1
(c) -1
(d) 3
Answer:

(A) is correct 1 1 1
Tricks:- Cyclic order
So, \(\frac{1}{\mathrm{x}}+\frac{1}{\mathrm{y}}+\frac{1}{\mathrm{z}}\) = 1
(See Quicker BMLRS)

Question 29.
If log x = m + n; log y = m – n then log\(\left(\frac{10 x}{y^2}\right)\) =
(a) 1 – m + 3n
(b) m – 1 + 3n
(c) m + 3n + 1
(d) None
Answer:
(a) If log x = m + n; log y = m – n
Then log\(\left(\frac{10 x}{y^2}\right)\)
= log 10 + log x – log y²
= 1 + log x – 2 log y
= 1 + (m + n) – 2(m – n)
= 1 + m + n – 2m + 2n
= 1 – m + 3n
∴ (a) is correct.

Question 30.
log₃ 5. × log₅ 4 × log₂ 3: [1 Mark, Dec. 2015]
(a) 2
(b) 5
(c) -2
(d) None of these
Answer:
(a) is correct log₃ 5. log₅ 4. log₂ 3
= log₃ 4. log₂ 3
= log₂ 4 = 2

Question 31.
The integral part of a logarithm is called __________, and the decimal part of a logarithm is called __________. [1 Mark, June 2016]
(a) Mantissa, Characteristic
(b) Characteristic, Mantissa
(c) Whole, Decimal
(d) None of these
Answer:
(b) is correct.

Question 32.
The value of \(\frac{1}{\log _3 60}+\frac{1}{\log _4 60}+\frac{1}{\log _5 60}\) = __________. [1 Mark, June 2016]
(a) 0
(b) 1
(c) 5
(d) 60
Answer:
(b) is correct. log₆₀ 3 + log₆₀ 4 + log₆₀ 5
= log₆₀(3 × 4 × 5) + log₂ 60 = 1

Question 33.
If log₄(x² + x) – log₄(x + 1) = 2 then the value of x is
(a) 2
(b) 3
(c) 16
(d) 8
Answer:
(c) is correct.

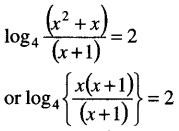
or log₄x – 2 ⇒ x = 4² = 16

Question 34.
Given log 2 = 0.3010 and log 3 = 0.4771 then the value of log 24 [1 Mark, Dec. 2016]
(a) 1.3081
(b) 1.1038
(c) 1.3801
(d) 1.8301
Answer:
(c) is correct.

Calculator Tricks:
Type 24 then √ button 19 times – 1 x 227695 = button. We will get the required value of log 24.

Question 35.
log (1³ + 2³ + 3³ + ………. + n³) = .[1 Mark, June 2017]
(a) 2 log n + 2 log (n + 1) – 2 log2
(b) log n + 2 log (n +1)-2 log2
(c) 2 log n + log (n +1)- 2 log 2
(d) None
Answer:
log (1³ + 2³ + 3³ + …………… + n³)
= log\(\left(\frac{n(n+1)}{2}\right)^2\) = 2log\(\frac{n(n+1)}{2}\)
= 2 [log n + log (n +1) – log 2]
= 2 log n + 2log(n+1) – 2log 2
So, (a) is correct

Tricks: Go by choices

Question 36.
If log₃[log₄(log_xx)] = 0 then X =
(a) 4
(b) 8
(c) 16
(d) 32
Answer:
(c)
Tricks: GBC
for option (c) log₃[log₄(log₂x)]
= log₃[log₄(log₂16)]
= log₃(log₄4) = log₃1 = 0
∴ (c) is correct.

Question 37.
If log\(\left(\frac{x-y}{2}\right)=\frac{1}{2}\)(log x + log y) then x² + y² = _______. [1 Mark, Dec. 2017]
(a) 6 xy
(b) 2xy
(c) 3x²y²
(d) 4x²y²
Answer:

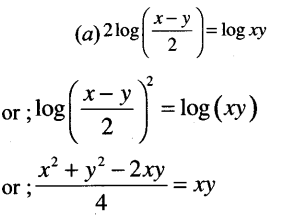
or; x² + y² – 2xy = 4xy
or; x² + y² =6xy

Question 38.
If log₂(3√2) = \(\frac{1}{15}\) then x = . [1 Mark, June 2018]
(a) 2
(b) 8
(c) 16
(d) 32
Answer:
(d) log₂(3√2) = \(\frac{1}{15}\)
or x^1/15 = 3√2 = 2^1/15
or x = (2^1/15)¹⁵ = 2⁵ = 32

Question 39.
The value of the expression :
alog_ab.log_b c. log_cd. log_dt. [1 Mark, Nov. 2018]
(a) t
(b) abcdt
(c) (a + b + c + d +1)
(d) None
Answer:
alog_ab.log_b c. log_cd. log_dt
= a^log_at = a^1.log_at = t¹ = t
[Formula a^xlog_ab = b^x]

Question 40.
log₂ log₂ log₂16 = ? [1 Mark, Nov. 2018]
(a) 0
(b) 3
(c) 1
(d) 2
Answer:
(c) log₂ log₂ log₂16 = log₂ log₂4 = log₂2 = 1

Question 41.
The value of
log₅(1+\(\frac{1}{5}\)) + log₅ (1 + \(\frac{1}{6}\)) + ……… + log₅ (1 + \(\frac{1}{624}\))
(a) 2
(b) 3
(c) 5
(d) 0
Answer:

Question 42.
log_{2\(\sqrt{2}\)} (512): log_{3\(\sqrt{2}\)} 324 = .[1 Mark, June 2019]
(a) 128:61
(b) 2:3
(c) 3 :2
(d) None
Answer:
Calculator Tricks
log_{2\(\sqrt{2}\)} (512) = 5 + 1
Type 2 × 2√ button = button.
Then press x button then continue pressing = button until to get 512
Here = button has been pressed 5 times. So log value
= No. of = button pressings + 1
Similarly For log_{3\(\sqrt{2}\)} 324
Type 3 × 2√ button = button then
x = button 3 times ; we get
log_{3\(\sqrt{2}\)}324 value = 3 + 1=4
So; log_{2\(\sqrt{2}\)}512:log_{3\(\sqrt{2}\)}324
= 6: 4 = 3: 2