Linear Equations – CA Foundation Maths Study Material

This Linear Equations – CA Foundation Maths Study Material is designed strictly as per the latest syllabus and exam pattern.

Linear Equations – CA Foundation Maths Study Material

The mathematical statement of equality is called Equation.

Linear Equation
The equation having highest power on the variable one is called linear equation. This is also called Equation of 1 variable.
Example
7x – 5 = 9.

Simultaneous Equation
Two or more linear equations having two or more variables is called simultaneous equation.
Example
3x + 2y = 10 &
2x + 3y = 2 are jointly called Simultaneous Equation.

Quadratic Equation (Equation of degree 2):
The equation of degree 2 is called Quadratic Equation or polynomial of degree 2.
Example
3x² + 5x + 6 = 0 is a Quadratic Equation.

Cubic Equation:
The equation of degree 3 is called Cubic Equation.
Example
4x³ + 3x² + 5x – 17 = 0 is a Cubic Equation.

Simple Equation
The Equation with one unknown variable x in the form ax + b = 0 is called Simple Equation. Where a ≠ 0.

Illustrative Examples
Example 1
The Equation -x + 1 = 5 – 2x will be satisfied for x equal to :
(a) 2
(b) 4
(c) 1
(d) None of these
Answer:
(b) is correct,
∵ -x + 1 = 5 – 2x.
or -x + 2x = 5 – 1.
or x = 4
Tricks
Do not solve such types of equation Go by choices. It takes minimum time.
Option (b)
Put x = 4 in the equation mentally and see
LHS – 4 + 1 = -3
RHS = 7 – 2 × 4 = -3
∴ LHS = RHS.
So option (b) is correct because it satisfies the equation.

Example-2
The value of y of fraction \(\frac{x}{y}\) exceeds with x by 5 and if 3 be added to both the fractions becomes \(\frac{3}{4}\). Find the fraction.
(a) \(\frac{12}{17}\)
(b) \(\frac{13}{17}\)
(c) –\(\frac{1}{3}\)
(d) None
Answer:
Option (a) is correct
y = x + 5
Fraction = \(\frac{x}{x+5}\)
From question = \(\frac{x+3}{x+5+3}=\frac{3}{4}\)
or \(\frac{x+3}{x+8}=\frac{3}{4}\)
or 4x + 12 = 3x + 24
or 4x -3x = 24 – 12
or x = 12.
Fraction = \(\frac{x}{x+5}=\frac{12}{12+5}=\frac{12}{17}\)
Option (a) is correct.
Tricks
Go by choices.
Let we see option (a) \(\frac{12}{17}\)
Clearly y = 17 is 5 more than x = 12.
Option (a) satisfies the 1st condition of the question.
If \(\frac{12+3}{17+3}=\frac{15}{20}=\frac{3}{4}\)
∴ Option (a) also satisfy 2nd condition of the equation.

Example-3
In a two digits number; the digit in the ten’s place is twice the digit in the unit’s place. If 18 be subtracted from the number the digits are reversed. Find the number.
(a) 63
(b) 21
(c) 42
(d) None
Answer:
(c) is correct.
Let x be the unit place digit.
So, Ten’s place digit = 2x.
∴ Number = 10x2x + x = 21x.
By question.
21x – 18 = 10x + 2x
or 21x – 12x = 18
or 9x = 18
∴ x = 2.
So, the required No. = 21x = 21 × 2 = 42
Tricks
Go by choices.
Option (a); (b) and (c) all satisfy 1st condition of the question.
i.e. in (a), (b), (c) Ten’s place digit is twice of unit place digit.
Let we see for 2nd condition.
(a) 63 – 18 = 45 ≠ 36 (Digits not reserved)
(b) 21 – 18 = 3 ≠ 12 (Digits not reserved)
(c) 42 – 18 = 24 (Digits reserved)
So option (c) also satisfies 2nd condition of the question.
∴ (c) is correct.

Example-4
For a certain commodity the demand equation giving “y” units for a price “p” in rupees per unit is y = 100 (10 – p). The supply equation giving the supply z units for a price “p” in rupees per unit isz = 75(p-3). The market price is such at which demand equals supply. Find the market price and quantity that will be brought and sold.
(a) ₹ 7; 300 units
(b) ₹ 8; 400 units
(c) ₹ 5; 200 units
(d) None
Answer:
(a) is correct.
Demand = Supply (given)
100 (10 – P) = 75 (P – 3)
or 40 – 4p – 3p – 9
or – 4p – 3p = -40 – 9
or – 7p = – 49
or p = 7
∴ y = 100 (10 – p) =100 (10 – 7) = 300 units
z = 75 (p – 3) = 75 (7 – 3) = 300 units.
∴ Price = ₹ 7 per unit.
Quantity = 300 units
∴ (a) is correct.
Tricks
Go by Choices
Option (a) satisfies given both conditions.

Previous Year Exam Questions

Question 1.
A man went to the Reserve Bank of India with ₹ 1,000. He asked the cashier to give him ₹ 5 and ₹ 10 notes only in return. The man got 175 notes in all. Find how many notes of ₹ 5 and ₹ 10 did he receive? [1 Mark, Feb. 2008]
(a) (25,150)
(b) (40,110)
(c) (150,25)
(d) None
Answer:
Tricks :
Go by choices
For (a) 25 × 5 + 150 × 10 ≠ Rs. 1000
(b) 40 × 5 + 110 × 10 ≠ Rs 1000
(c) 150 × 5 + 25 × 10 = Rs 1000
(c) is correct

Question 2.
A man rowing at the rate of 5 km in an hour in still water takes thrice as much time in going 40 km up the river as in going 40 km down. Find the rate at which the river flows: [1 Mark, June 2008]
(a) 9 km/hr
(b) 10 km/hr
(c) 12 km/hr
(d) None
Answer:
Tricks : Go by choices
Given Distance = 40 km
(a) t = \(\frac{40}{9-5}\) (upstream) = 10hrs
Down Stream t = \(\frac{40}{9+5}=\frac{40}{14}=\frac{20}{7}\) hrs
∴ (a) is not correct.

(b) Down stream t = \(\frac{40}{10+5}=\frac{40}{15}=\frac{8}{3}\)
Upstream, t = \(\frac{40}{10-5}=\frac{40}{5}\)hrs
Clearly; 8 = 3 × \(\frac{8}{3}\)
∴ (b) is correct

Question 3.
The point of intersection of the lines 2x – 5y = 6 and x + y = 3 is . [1 Mark, Dec. 2009]
(a) (0, 3)
(b) (3, 0)
(c) (3, 3)
(d) (0, 0)
Answer:
(b) Tricks : Go by choices.
Intersecting Point lies on both straight lines. It will satisfy both eqns.
∴ For (a) (0,3) Point 2 × 0 – 5 × 3 ≠ 6
∴ It is incorrect
Option (b) (3 ; 0) satisfies both eqns.
∴ (b) is correct.

Question 4.
If the length of a rectangle is 5 cm more than the breadth and if the perimeter of the rectangle is 40 cm, then the length & breadth of the rectangle will be: [1 Mark, Dec. 2009]
(a) 7.5 cm, 2.5 cm
(b) 10cm, 5cm
(c) 2.5 cm, 7.5cm
(d) 15.5cm, 10.5cm
Answer:
(c) Tricks : Go by choices.
1st condition = length is 5cm more than breadth
All option satisfy this condition
II Perimeter = 2(l+b) = 40 of rectangle
Only option (c) satisfies it
∴ (c) is correct.

Detail Method
Let breadth = x ;Length = x + 5
Perimeter = 40
2 (x+ 5 + x) = 40
or 2x + 5 = 20
or x = \(\frac{15}{2}\) = 7.5cm
∴ Length = x + 5 = 7.5 + 5 = 12.5
Breadth = x = 7.5 cm
∴ (c) is correct

Question 5.
For all λ ∈ R , the line (2 + λ)x + (3 – λ) y + 5 = 0 passing through a fixed point, then the fixed point is _________. [1 Mark, June 2011]
(a) (1, 1)
(b) (-1, -1)
(c) (1, -1)
(d) (-1, 1)
Answer:
(b)
Tricks : Go by choices
For option (b) Point (-1 ; -1) satisfies the eqn.
LHS = =(2 + λ)x + (3 – λ)y + 5
or (2 + 2)(-1) + (3 – 2)(-1) + 5
= -2 – λ – 3 + λ + 5 = 0 = RHS.
∴ (b) is correct

Question 6.
If kx – 4 = (k – 1).x which of the following is true. [1 Mark, Dec. 2013 ]
(a) x = -5
(b) x = -4
(c) x = -3
(d) x = 4
Answer:
(d) is correct kx – 4 = (k – 1) x
or kx – 4 = kx – x
or -4 = -x
∴ x = 4

Question 7.
If the equations kx + 2y = 5, 3x + y = 1 has no solution then the value of k is: [1 Mark, Dec. 2013]
(a) 5
(b) 2/3
(c) 6
(d) 3/2
Answer:
(c) is correct kx + 2y = 5
3x + y = 1
They have no soln. (given) \(\frac{k}{3}=\frac{2}{1} \neq \frac{5}{1}\) ⇒ -k = 6

Question 8.
The equation x + 5y = 33; \(\frac{x+y}{x-y}=\frac{13}{3}\) has the solution (x,y) as: [1 Mark, Dec. 2014]
(a) (4, 8)
(b) (8, 5)
(c) (4, 16)
(d) (16, 4)
Answer:
(b) is correct
Tricks: Go by choices
For LHS = x + 5y = 8 + 5 × 5 = 33
and \(\frac{x+y}{x-y}+\frac{8+5}{8-5}=\frac{13}{3}\)
Clearly (b) satisfies both eqns.

Question 9.
The age of a person is 8 years more than thrice the age of the sum of his two grandsons who were twins. After 8 years his age will be 10 years more than twice the sum ofthe ages of his grandsons. Then the age of the person when the twins were bom is: [1 Mark, June 2015]
(a) 86 yrs
(b) 73 yrs
(c) 68 yrs
(d) 63 yrs
Answer:
(b) Let age of 1st grandson = x
∴ Person’s Age = P = 3(x + x) + 8
P = 6x + 8
After 8 years P + 8 = 2 [x + 8 + x + 8] + 10 = 2(2x+ 16)+ 10
or 6x + 8 + 8 = 4x + 32 + 10
or 2x = 42 – 16 =26
∴ x = 13
∴ Age of person when grandsons were born = 6x + 8 – x = 6 × 13 + 8 – 13 = 73
(b) is correct

Question 10.
In a school number of students in each section is 36. If 12 new students are added, then the number of sections are increased by 4 and the number of students in each section becomes 30. The original number of section at first is: [1 Mark, June 2015]
(a) 6
(b) 10
(c) 14
(d) 18
Answer:
(d); Let original No. of sections = x
Total students = 36x
Again Qts.
36x + 12 = (x+4).30
or 36x + 12 = 30 x + 120
or 6x= 108 ⇒ x = 18
Tricks: Go by choices

Question 11.
A person on a tour has ₹ 9600 for his expenses. But the tour was extended for another 16 days, so he has to cut down his daily expenses by ₹ 20.The original duration of the tour had been ? [1 Mark, June 2015]
(a) 48 days
(b) 64 days
(c) 80 days
(d) 96 days
Answer:
(c); Let No. of tour days = x
∴ Expense per day = \(\frac{9600}{x}\)
Now Expense per day = \(\frac{9600}{x+16}\)
From \(\frac{9600}{x}-\frac{9600}{x+16}\) = 20
Tricks Go by choices
From here we get
For (c) LHS
\(\frac{9600}{80}-\frac{9600}{80+16}\) = 20 RHS
(c) is correct
Do by Calculator

Question 12.
If 2^x+y = 2^2x-y = √8 then the respective values of x and y are _________. [1 Mark, June 2016]
(a) 1, \(\frac{1}{2}\)
(b) \(\frac{1}{2}\), 1
(c) \(\frac{1}{2}\), \(\frac{1}{2}\)
(d) None of these
Answer:
(a) is Correct. 2^x+y= 2^2x-y = √8 = \(\sqrt[2]{2^3}\) = 2^3/2
∴ x + y = \(\frac{3}{2}\) (1)
2x – y = \(\frac{3}{2}\) (2)
Tricks: Then Go by Choices
(a) satisfies (1) & (2) both.

Question 13.
Let E₁, E₂ are two linear equations in two variables x and y .(0,1) is a solution for both the equations E₁ & E₂ (2, -1) is a solution of equation E, only and (-2, -1) is a solution of equation E₂ only, then E₁, E₂ are _________. [1 Mark, June 2016]
(a) x = 0, y = 1;
(b) 2x – y = -1, 4x + y = 1
(c) x + y = 1, x – y = -1
(d) x + 2y = 2, x + y = 1
Answer:
(c) is correct.
Tricks: Go by Choices
(0 ; 1) satisfies E₁ & E₂ both
(2,-1) satisfies 1st Eqn. 2 – 1 = 1 (True)
But (-2 ; -1) also satisfies E₂
i.e. -2 -(-1) = -1 (True)

Question 14.
Particular company produces some articles on a day. The cost of production per article is ₹ 2 more than thrice the number of articles and the total cost of production is ₹ 800 on a day then the number of articles is : [1 Mark, Dec 2016]
(a) 16
(b) 14
(c) 18
(d) 15
Answer:
(a) is correct.
TRICKS : Go by choices Let (A) is correct.
So, cost per unit = 800/16 = ₹ 50
It is 2 more than 3 times of 16.
(as given in Qts.)

Question 15.
The sides of equilateral triangle are shortened by 3 units, 4 units, 5 units respectively then a right angle triangle is formed. The side of the equilateral triangle was: [1 Mark, June 2017]
(a) 5
(b) 6
(c) 8
(d) 10
Answer:
Tricks : Go by Choices
For option (c)
1 st side of right angled Δ = 8 – 3 = 5
2nd side = 8 – 4 = 4
and 3rd side = 8 – 5 = 3
Here ; 5 ; 4 and 3 are making a right angled triangle.
So, 5² = 4² +3²
Hence, option (c) is correct.

Question 16.
If \(\frac{3}{x+y}+\frac{2}{x-y}\) = -1 and \(\frac{1}{x+y}-\frac{1}{x-y}=\frac{4}{3}\) then (x, y) is: [1 Mark, June 2017]
(a) (2, 1)
(b)( 1, 2)
(c) (-1,2)
(d) (-2, 1)
Answer:
Tricks: Go by Choices
Option (B)
\(\frac{3}{1+2}+\frac{2}{1-2}\) = -1 (True)
\(\frac{1}{1+2}-\frac{1}{1-2}=\frac{1}{3}+1=\frac{4}{3}\) (True)
So; option (B) is correct.

Question 17.
The line 3x + 2y = 6 intersects the line 3 x – y = 12 in _________ quadrant: [Dec.-2017]
(a) 1st
(b) 2nd
(c) 3rd
(d) 4th
Answer:
(d), Eqn. (1) – Eqn. (2); we get

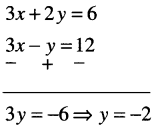
From (1); 3x = 6 – 2y = 6 – 2(-2) = 10
∴ x = \(\frac{10}{3}\)
∴ Co-ordinate of the point of intersection
= (x, y) = (\(\frac{10}{3}\), -2)
It is in 4th Quadrant.

Question 18.
If 2^x+y = 2^2x-y = √8, then the respective values of x and y ……….. [1 Mark, May 2018]
(a) 1, \(\frac{1}{2}\)
(b) \(\frac{1}{2}\), 1
(c) \(\frac{1}{2}\), \(\frac{1}{2}\)
(d) None
Answer:
(a)
2^x+y = 2^2x-y = √8 = (2³)^1/2
= 2^3/2
Tricks:- Go by Choices (GBC)
(a) 2^{1+\(\frac{1}{2}\)} = 2^{\(\frac{3}{2}\)} = RHS and 2^{2×1-\(\frac{1}{2}\)} = 2\(\frac{3}{2}\) = RHS
∴ (a) is correct

Question 19.
If \(\frac{3}{x+y}+\frac{2}{x-y}\) = -1; \(\frac{1}{x+y}-\frac{1}{x-y}=\frac{4}{3}\); then (x, y) is: [1 Mark, May 2018]
(a) 2, 1
(b) 1, 2
(c) -1, 2
(d) -2, 1
Answer:
(b) is correct
Tricks: Go by choices.

Question 20.
If the sides of an equilateral triangle are shortened by 3 units , 4 units and 5 units respectively and a right triangle is formed then the sides of an equilateral triangle is: [1 Mark, May 2018]
(a) 6 units
(b) 7 units
(c) 8 units
(d) 10 units
Answer:
(c) is correct.
Tricks:- Go by Choices.
Check for option (a).
1st Side = 6 – 3 = 3
2nd Side = 6 – 4 = 2
3rd Side = 6 – 5 = 1
But 1² + 2² ≠ 3²
[Note Try to do it mentally]
So (a) is False.
(c) 1st Side = 8 – 3 = 5
2nd Side = 8 – 4 = 4
3rd Side = 8 – 5 = 3
But 3² + 4² = 5² (True)
(Pythagoras Formula)
(c) is correct.

Question 21.
A number consists of two digits such that the digit in one’s place is thrice the digit at ten’s place. If 36 be added then the digits are reversed. Find the number: [1 Mark, June 2019]
(a) 62
(b) 26
(c) 39
(d) None
Answer:
(b)
Tricks :- Go by choices
(a) 62 → 2 ≠ 3 × 6 (False)
and 62 + 36 = 98 ≠ 26 (False)

(b) 26 Clearly 6 = 3 × 2 (True)
and 26 + 36 = 62 (Orders of digits reversed)
So; (b) is correct.