Integral Calculus – CA Foundation Maths Study Material

This Integral Calculus – CA Foundation Maths Study Material is designed strictly as per the latest syllabus and exam pattern.

Integral Calculus – CA Foundation Maths Study Material

Previous Year Exam Questions

Question 1.
\(\int_0^1\)(e^x + e^-x) dx is:
(a) e – e^-1
(b) e^-1 – e
(c) e + e¹
(d) None
Solution :
(a) is correct

= e – 1 – e^-1 + 1 = e – e^-1

Question 2.
∫\(\frac{8 x^2}{\left(x^3+2\right)^3}\)dx is equal to: [1 Mark, Nov. 2006]
(a) –\(\frac{4}{3}\)(x³ + 2) + C
(b) –\(\frac{4}{3}\)(x³ + 2)^-2 + C
(c) \(\frac{4}{3}\)(x³ + 2)² + C
(d) None of these
Answer:

Question 3.
∫\(\frac{d x}{\sqrt{x^2+a^2}}\):
(a) \(\frac{1}{2}\)log(x + \(\sqrt{x^2+a^2}\)) + C
(b) log(x + \(\sqrt{x^2+a^2}\)) + C
(c) log(x\(\sqrt{x^2+a^2}\)) + C
(d) \(\frac{1}{2}\)log(x\(\sqrt{x^2+a^2}\)) + C
Answer:
(b) is correct
I. Remember it as Formula
Trick II. Go by choices
Differentiation of which option is the Integration of given Function
Here to differentiate is more easy than to Integrate.

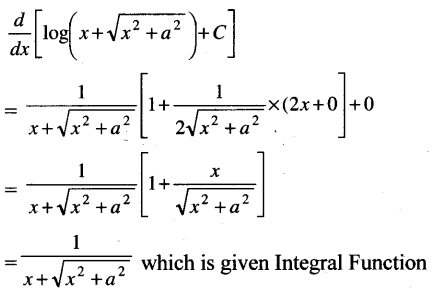
III Detail Method
Let t – x = \(\sqrt{x^2+a^2}\)

Question 4.
The value of \(\int_0^2 \frac{\sqrt{x}}{\sqrt{x}+\sqrt{2-x}}\)dx is: [1 Mark, Feb. 2007 & May 2007]
(a) 0
(b) 3
(c) 2
(d) 1
Answer:
(d) is correct

2I = 2; I = 1

Question 5.
The Integral of (e^3x + e^-3x)/e^x is: [1 Mark, May 2007]
(a) \(\frac{e^{2 x}}{2}+\frac{e^{-4 x}}{4}\) + C
(b) \(\frac{e^{2 x}}{2}-\frac{e^{-4 x}}{4}\) + C
(c) e^2x – e^-4x
(d) None of these
Answer:
(b) is correct

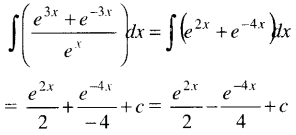
Where c = Integration (Arbitrary) Constant.

Question 6.
∫x²e^3xdx is:
(a) x².e^3x – 2xe^3x + 2e^3x + C
(b) \(\frac{e^{3 x}}{3}-\frac{x \cdot e^{3 x}}{9}\) + 2e^3x + C
(c) \(\frac{x^2 \cdot e^{3 x}}{3}-\frac{2 x \cdot e^{3 x}}{9}+\frac{2}{27}\)e^3x + C
(d) None of these
Answer:
(c) is correct.
By parts; we get

Question 7.
\(\int_1^2 \frac{2 x}{1+x^2}\)dx: [1 Mark, May & Aug. 2007]
(a) log_e\(\frac{5}{2}\)
(b) log_e5 – log_e2 + 1
(a) log_e\(\frac{2}{5}\)
(d) None of these
Answer:
(a)

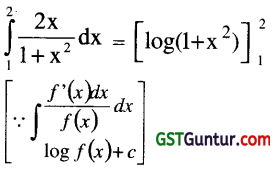
= log(1+2²) – log(1 + 1²)
= log 5 – log 2 = log\(\frac{5}{2}\)
(a) is correct

Question 8.
The value of \(\int_1^e \frac{(1+\log x)}{x}\)dx is: [Given Loge = 1]. [1 Mark, Aug. 2007]
(a) 1/2
(b) 3/2
(c) 1
(d) 5/2
Answer:
(b) is correct

Question 9.
Find ∫\(\frac{x^3}{\left(x^2+1\right)^3}\)dx: [1 Mark, Aug. 2007]

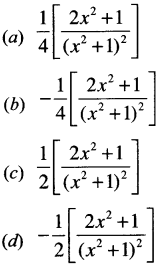
Answer:
(b) is correct

Question 10.
∫\(\frac{1}{x^2-a^2}\)dx is: [1 Mark, Nov. 2007]
(a) log(x – a) – log(x + a) + C
(b) log x – \(\frac{a}{x+a}\) + C
(c) \(\frac{1}{2 a}\) log\(\left(\frac{x-a}{x+a}\right)\) + C
(d) None of these
Answer:
(c) is correct

Where c = Integration Constant

Question 11.
The value of \(\int_0^1 \frac{d x}{(1+x)(2+x)}\) is : [1 Mark, Nov. 2007]
(a) log \(\frac{3}{4}\)
(b) log \(\frac{4}{3}\)
(c) log 12
(d) None of these
Answer:
(b) is correct
\(\int_0^1 \frac{d x}{(1+x)(2+x)}\)
By Hit & Trial Method; we get
= \(\int_0^1\left(\frac{1}{1+x}-\frac{1}{2+x}\right)\)dx
= [log(1 + x)]¹₀ – [log(2 + x)]¹₀
= [log(1 + 1)- log(1 + 0)] – [log(2 + 1) – log(2 + 0)]
= log2 – 0 – log3 + log2
= 2log2 – log3
= log2² – log3 = log\(\frac{4}{3}\)

Question 12.
The value of \(\int_2^3\)(5 – x)dx – \(\int_2^3\)f(x)dx is:
Answer:
(b) is correct.

Question 13.
∫\(\frac{e^{\log _{e x} x} d x}{x}\) is:
(a) x^-1 + C
(b) x + c
(c) x² + C
(d) None
Answer:
(b) is correct
∫\(\frac{e^{\log _e x} d x}{x}\) = ∫\(\frac{x}{x}\)
[Formula a^{x log_ab} = b^x]
= ∫dx = x + c

Question 14.
Evaluate ∫\(\frac{1}{(x-1)(x-2)}\)dx: [1 Mark, June 2008]
(a) log \(\left(\frac{x-2}{x-1}\right)\) + C
(b) log[(x – 2)(x -1)] + C
(c) \(\left(\frac{x-1}{x-2}\right)\) + C
(d) None
Answer:
(a) is correct,
∫\(\frac{1}{(x-1)(x-2)}\) = ∫\(\left(\frac{1}{(x-2)}-\frac{1}{x-1}\right)\)
(By Hit & Trial method)
= log(x – 2)- log(x -1)+ c
= log\(\left(\frac{x-2}{x-1}\right)\) + c

Question 15.
\(\int_1^4\)(2x + 5) dx and the value is: [1 Mark, June 2008]
(a) 10
(b) 3
(c) 30
(d) None
Answer:
(c) Is correct.

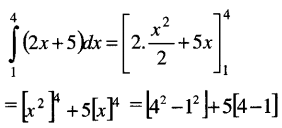
= 15 + 15 = 30

Question 16.
∫\(\frac{1}{x\left(x^5-1\right)}\)dx

Answer:
(b) is correct