Foreign Exchange Exposure and Risk Management – CA Final SFM Study Material

Foreign Exchange Exposure and Risk Management – CA Final SFM Study Material is designed strictly as per the latest syllabus and exam pattern.

Foreign Exchange Exposure and Risk Management – CA Final SFM Study Material

Part-1(Theory)

Question 1.
Write a short note on the following:
Arbitrage operations [Nov. 2008] [5 Marks]
Answer:
Arbitrage means making riskless profits without any investment. It is buying and selling the same commodity in the different markets at the same time at such a price that the buying is always less than the selling price, so that the profits are certain. A number of pricing relationships exist in the foreign exchange market, and at times an opportunity may arise for making arbitrage profits even if for a small moment of time. An arbitrageur takes the benefit of price differentials. For example, in case of foreign currency exchange rates, there could be a direct exchange rate and another through cross currency rates and if the bid of one is more than the ask rate of another, there will be an arbitrage opportunity.

Question 2.
Write a short note on the following:
Leading and Lagging [Nov. 2011] [4 Marks]
Answer:
Leading and lagging are the methods of hedging risk due to foreign currency exposure or a means to take advantage of the foreign exchange rate fluctuations. Leading means making the payment before the due date, i.e. advancing a payment. It is resorted to by the payer if he apprehends appreciation in currency in which the payment is to be made. The payer will have to arrange the money which he will convert into the foreign currency to make the pre-payment. Therefore, the costs of this fund should not exceed the expected appreciation in foreign currency, on the other hand, lagging means delaying the payment. If the payer anticipates that there will be fall in the currency in which the payment is to be made, he will like to lag the payment. The benefit of lagging should be more than the interest cost in delaying the payment. The purpose of both lagging and leading is to reduce the debt burden.

Another purpose of leading and lagging is also shifting the liquidity by modifying the credit terms between inter-group entities. The decision regarding leading and lagging should be taken on the basis of cost of funds to both paying entity and receiving entity. If paying and receiving entities have different home currencies, likely movements in exchange rate fluctuations should also be considered.

Question 3.
Write short note on the following:
Nostro, Vostro and Loro Accounts [May 2012] [4 Marks]
Answer:
Nostro, is an account, which is maintained by a bank in one country, with a bank in a foreign country. It is in the home currency of that foreign country. For Example, if a bank in India maintains an account with a bank in America and money is held in $ or in Britain in £. The Indian Bank will refer the Account as Nostro Account in correspondence with the foreign bank. It means “Our A/c with you.” All foreign exchange transactions are routed through Nostro account. The foreign bank will refer this account as Vostro Le. “your Account with us”. So, a “Vostro Account” on the other hand is an account by a foreign bank in India held in Rs. The Indian bank will call this A/c as Vostro account. For exchange control purposes such accounts are known as “ non-resident bank accounts”.

Loro Account is an account wherein a Bank remits funds in foreign currency to another Bank for credit to an account of a third Bank. It means “their account with you”. For example if SBI has an A/c with Citi bank US in $, then for SBI it is Nostro A/c, for Citi bank it is Vostro A/c and when the same A/c is referred by HDFC India in its correspondence with Citi Bank, for HDFC it is LORO A/c.

Question 4.
Write short note on the following:
Forward Rate Agreements (FRA) [May 2014] [4 Marks]
Answer:
FRA’s are an effective tool for managing risk in interest rates if the requirement is to borrow or lend money after a specific period for a fixed tenure.
Features of FRA:
(a) They are a kind of over the counter derivative, and are not exchange traded.
(b) It is normally used by banks to fix interest costs on anticipated future deposits or interest revenues on variable rate, loan indexed to LIBOR.
(c) It is an off Balance sheet instrument.
(d) There is no transfer of principal.
(e) The buyer of the FRA fears rise in interest rate as he is a borrower. If rate of interest actually rises he is compensated. He may bear loss if rate of interest falls.
(f) The seller of FRA fears fall in interest rates and he is looking forward to lend or deposit money in the future and he is compensated if rate actually falls. But he will have to bear loss if the rate of interest rises.
(g) It is settled at maturity in cash representing the profit or loss.

Question 5.
Write short note on the following:
What are the risks to which foreign exchange transactions are exposed? [Nov. 2014] [4 Marks]
Answer:
A firm dealing with foreign exchange may be exposed to foreign currency fluctuations. The exposure is the result of possession of assets and liabilities and transactions denominated in foreign currency. When exchange rate fluctuates, assets, liabilities, revenues and expenses that are expressed in foreign currency will result in either gain or loss. The following types of risks are present for a firm dealing with foreign exchange.

Transaction exposure; a firm may have some contractually fixed payments and receipts in foreign currency, such as import payables, export receivables, interest payable on foreign currency loans etc. All such items are to be settled in a foreign currency. Unexpected fluctuation in exchange rate will have favourable or adverse impact on its cash flows.
Translation exposure; it is basically the exposure on the assets and liabilities shown in the balance sheet and which are not going to be liquidated in the near future.

Economic exposure; it measures the probability that fluctuations in foreign exchange rate will affect the value of the firm is calculated by discounting the expected future cash flows with appropriate discounting rate.

Question 6.
Write short note on the following:
Operations in foreign exchange market are exposed to number of risks. [May 2016] [4 Marks]
Answer:
Transaction exposure: A firm may have some contractually fixed payments and receipts in foreign currency, such as, import payables, export receivables, interest payable on foreign currency loans etc. all such items are to be done in foreign currency. Unexpected fluctuations in exchange rate may have favourable or adverse impact on its cash flows. Such exposures are termed as transactions exposures.

Translation exposure: Also known as the accounting exposure or the Balance sheet exposure it is basically the exposure on the assets and liabilities shown in the balance sheet and which are not going be liquidated in near future. It refers to the probability of loss that the firm may have to face because of decrease in value of assets due to devaluation of a foreign currency despite the fact that there was no foreign exchange transactions during the year.

Economic exposure: Economic exposures measures the probability that fluctuations in foreign exchange rate will effect the value of the firm.

The intrinsic value of the firm is calculated by discounting the expected future cash flows with appropriate discounting rate. The risk involved in economic exposure requires measurement of the effect of fluctuations in exchange rate on different future cash flows.

Question 7.
Write short note on the following:
Briefly explain the main strategies for exposure management. [May 2017] [4 Marks]
Answer:
Strategies for exposure management are
1. Low risk, low reward
This option involves automatic hedging of exposures in the forward market as soon as they arise, irrespective of the attractiveness or otherwise of the forward rate.

2. Low risk, reasonable reward
This strategy requires selective hedging of exposures whenever forward
rates are attractive but keeping exposures open whenever they are not.

3. High risk low reward
Perhaps the worst strategy is to leave all exposures un-hedged.

4. High risk, high reward;
This strategy involves active trading in the currency market through continuous cancellations and re-bookings of forward contracts. With exchange controls relaxed in India in recent times, a few of the larger companies are adopting this strategy.

Question 8.
Answer the following
Explain the significance of LIBOR in international financial transactions. [May 2011] [4 Marks]
Answer:
Libor stands for London inter-bank offer rate. Other features of Libor are as follows;
It is the base rate of exchange with respect to which most international financial transaction are priced.
It is used as the base rate for a large number of financial products such as options and swaps.
Banks also use the libor as the base rate when setting the interest rate on loans, savings and mortgages.
It is mentioned by large number of professionals and private individuals worldwide.

Question 9.
What is the meaning of:
(i) Interest rate parity
(ii) Purchasing power parity. [May 2011] [4 Marks]
Answer:
(i) Interest Rate Parity: The Purchasing power parity gives the equilibrium in the commodity market. The equivalent in the financial market is the theory called the Interest rate parity (IRP) or the covered interest parity condition. According to this theory, the cost of covering foreign exchange risk is equal across different currencies. This is so because in the absence of any transaction costs, taxes and capital controls, investors will tend to transact in those currencies which provide them the most attractive prices. Besides, the arbitrageurs will always be on the look – out for an opportunity to make riskless profits. The resultant effects on the demand and supply would drive the value of currencies towards equalization. Thus, the size of the forward premium or discount should be equal to the interest rate differential between the two countries of concern. The equation is given by:
Forward rate = Spot rate $\left[\frac{1+\text { Interest rate in domestic currency }}{1+\text { Interest rate in foreign currency }}\right]^t$

(ii) Purchasing Power Parity: The Purchasing power parity was enunciated by a Swedish economist Gustav Cassel in 1918. According to the theory, the price levels in different countries determine the exchange rates of the currencies of these countries. This law is based on the law of one price. It is based on the following assumptions:
(a) There is no restriction on movement of goods between the countries.
(b) Commodities can be transported.
(c) There are no transportation costs.
(d) The commodities are homogenous.
Since the spot rate is determined by price level in two countries, the spot rate expected on a future date depends on the change in price levels in two countries during period between the current date and future date.

According to Purchasing Power Parity
Forward rate = Spot rate $\left[\frac{1+\text { Annual Inflation rate in domestic currency }}{1+\text { Annual Inflation rate in foreign currency }}\right]^t$
There are three forms of PPP theory one is “The Absolute Form” as discussed above and the other is the “The Relative form” which accounts for the possibility of market imperfections such as transportation costs tariffs and quotas.
The third form is the expectation form. According to this form, the expected percentage change in the spot rate is equal to the difference in the expected inflation rates in the two countries.

Question 10.
Write short note on’‘Exposure Netting.”
Answer:
Exposure Netting refers to offsetting exposures in one currency with exposures in the same or another currency, where exchange rates are expected to move in such a way that losses or gains on the first exposed position should be offset by gains or losses on the second currency exposure.

The objective of the exercise is to offset the likely loss in one exposure by likely gain in another. This is a manner of hedging foreign exchange exposures though different from forward and option contracts. This method is similar to portfolio approach in handling systematic risk.

For example, let us assume that a company has an export receivables of US$ 10,000 due 3 months hence, if not covered by forward contract, here is a currency exposure to US$.

Further, the same company imports US$ 10,000 worth of goods/commodities and therefore also building up a reverse exposure. The company may strategically decide to leave both exposures open and not covered by forward, it would be doing an exercise in exposure netting.

Despite the difficulties in managing currency risk, corporates can now take some concrete steps towards implementing risk mitigating measures, which will reduce both actual and future exposures. For years now, banking transactions have been based on the principle of netting, where only the difference of the summed transactions between the parties is actually transferred. This is called settlement netting. Strictly speaking in banking terms this is known as settlement risk. Exposure netting occurs where outstanding positions are netted against one another in the event of counter party default.

Part-2(Numerical Problems: Topic)

Question 1.
If the exchange rate (₹ /$) is 65.25/65.90 and 3 months swap points are 50/30
(i) Identify, whether this is a direct quote for an Indian or an indirect quote. What is the spot bid rate and spot ask rate.
(ii) Find the inverse (Indirect quote) spot rate.
(iii) How much $ should one pay to get ? 20,00,000.
(iv) What amount will a person receive if he sells $1,00,000.
(v) What will be the exchange rate after 3 months?
(vi) Is Dollar at Premium or Discount after 3 months?
(vii) Find the annualized premium/discount per cent.
(viii) How much amount is to be paid in order to receive $5,00,000 after 3 months? [Practice Question]
Answer:
(i) This is a direct quotation for an Indian. The spot bid rate is ₹ 65.25 and the spot ask rate is ₹ 65.90

(ii) When inverse quotation is determined

(iii) Amount of dollars to be paid to get ₹ 20,00,000 = $\frac{20,00,000}{65.25}$
= $ 30651.34
Alternatively by using indirect quotation of $\left(\frac{\$ .}{R s .}\right)$ Ask
20,00,000 × 0.015325 = $ 30650 (approx.)

(iv) Selling $ 1,00,000 means bid rate of direct quotation will be applicable. This means the person will receive 1,00,000 × 65.25 = ₹ 65,25,000

(v) Exchange rate after 3 months will be determined on the basis of Swap points. Since, these points are in decreasing order, they will be subtracted from spot rate to arrive at the forward rate.
Therefore, 3 months forward rate = 64.75/65.60 (65.25-0.50/65.90-0.30)

(vi) The dollar is at discount after 3 months.

(vii) Calculation of forward Discount on $. = $\frac{\text { Forward rate }- \text { Spot Rate }}{\text { Spot Rate }}$ × 100

Bid rate:	Ask rate:
= $\frac{64.75-65.2}{65.25}$ × 100 (-) 0.766% for 3 months	$\frac{65.60-65.90}{65.90}$ × 100 (-)0.4552% for 3 months
0.766 × $\frac{12 \text { Months }}{3 \text { Months }}$ = 3.064%	0.4552 × \( = 1.80209%

(viii) To receive dollar 5,00,000 after 3 months the person will have to pay 5,00,000 × 65.60 = ₹ 3,28,00,000.

Question 2.
An extract from exchange rate list of a Kolkata based bank is given below: ₹ /¥ 0.3992 : 0.4002
(i) How many Yen will it cost for a Japanese tourist visiting India to purchase ₹ 25,000 worth of television?
(ii) How much will Mr. Basu in Kolkata have to spend in rupees, to purchase a Sony Camera worth Yen 1,25,000 ? [Practice Question]
Answer:
The Exchange rate of ₹ /¥ is 0.3992/0.4002
The rate 0.3992 is the bid rate at which bank will purchase ¥ from the Japanese tourist and 0.4002 is the ask rate at which the bank will sell ¥ to him.
(i) If Japanese tourist is purchasing something in ₹, he will need to buy ₹ against Yen, and he will sell ¥ to get the ₹, therefore bank will buy ¥.
The bid rate will be applicable = [latex]\frac{R s .25,000}{R s .0 .3992}\) = ¥62625.25

(ii) Mr. Basu will need 1,25,000 ¥ to buy Sony Camera. He will buy Yen from the bank and the bank will sell¥. The ask rate will be applicable. Mr. Basu will have to pay (¥ 1,25,000 × 0.4002) = ₹ 50,025

Question 3.
Consider the following rates:

Spot Rate		3 month Forward Rate
₹/$	42.17/42.59	₹/$	43.15/43.60
₹/DM	24.61/25.10	₹/DM	25.36/25.90

(i) From these rates, calculate the spot and forward DM/$ rates.
(ii) What are the upper and lower boundaries for the DM/$ quotations? [Practice Question]
Answer:
(i) The rate of (DM/$) will be the cross currency rate as direct quote is not available. The upper and lower boundaries will be the bid and the ask rate.
The rates available are:

Quote	Spot	Forward
(₹ /$) bid	42.17	43.15
(₹ /$) ask	42.59	43.60
(₹ /DM) bid	₹ 24.61	25.36
(₹ /DM) ask	₹ 25.10	25.90

From above available rates we can compute required rate as follows:

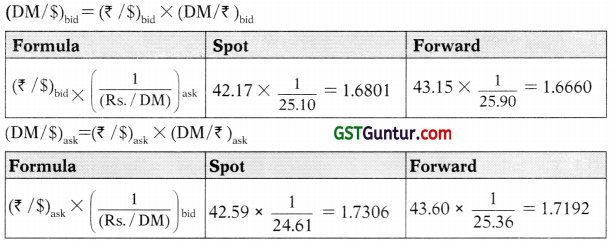
(ii)

Rate DM/$	Lower Boundary (Bid)	Upper Boundary (Ask)
Spot DM/$	1.6801	1.7306
Forward DM/$	1.6660	1.7192

Question 4.
An Indian customer who has imported equipment from Germany has approached a bank for booking a forward Euro contract. The delivery is expected six months from now. The following rates are quoted:

$/Euro Spot	0.8453/0.8457	₹ /$ Spot	46.47/46.57
6m-Swap points	15/20	6m-Swap points	20/30

What rate the bank will quote, if it needs a margin of 0.5%?
Answer:
The Spot Exchange rate of ₹ /$ is 46.47/46.57
The Spot Exchange rate of $/€ is 0.8453/0.8457
The 6 months forward exchange = (Original rate + swap points)
Rate of ₹ /$:
(46.47 + 0.20/46.57 + 0.30)
= 46.67/46.87
Rate of $/€:
(0.8453 + 0.0015/0.8457 + 0.0020)
= 0.8468/0.8477
The 6 month forward rate of ₹ /€ will be the cross currency rate, as direct quote is not available.
(₹ /€)_bid = (₹/$)_bid × ($/€.)_bid
= 46,67 × 0,8468 = 39.52
(₹/€)_ask = (₹/$)_ask × ($/€)_ask
46.87 × 0.8477 = 39.73
₹/€ = 39.52/39.73
The Indian importer will buy €, so ask rate of ₹ 39.73 will be applicable. Add to this, the bank’s margin of 0.5%, the rate quoted by the bank will be ₹/€ = 39.93 (39.73 + 0.5%).

Question 5.
The following 2-way quotes appear in the foreign exchange market:

RS/US$	Spot	2-months forward
	₹ 46.00/₹ 46.25	₹ 47.00/₹ 47.50

Required:
(i) How many US dollars should a firm sell to get ₹ 25 lakhs after 2 months?
(ii) How many Rupees is the firm required to pay to obtain US $ 2,00,000 in the spot market?
(iii) Assume the firm has US $ 69,000 in current account, earning no interest. (ROI) on Rupee investment is 10% p.a. Should the firm encash the US $ now or 2 months later? [June 2009] [6 Marks]
Answer:
(i) US $ required to get ₹ 25 Lakhs after 2 months at the Rate of ₹ 47/$
$\frac{25,00,000}{47}$ = US$ 53,191.49
(ii) ₹ required to get US$ 2,00,000 now at the rate of 7₹ 46.25/$
US $ 2,00,000 × ₹ 46.25 = ₹ 92,50,000
(iii) Encashing US $ 69000 now or 2 month later:

Particulars	Calculation	Amount
Proceeds, if encashed in the open market	$ 69000 × ₹ 46	₹ 31,74 ,000
Interest earned	31,74,000 × $\frac{10}{100}$ × $\frac{2}{12}$	₹ 52,900
Likely sum at the end of 2 months	(31,74,000 + 52,900)	32,26,900
If encashed after 2 months, using forward rate	$ 69000 × ₹ 47.00	32,43,000

Conclusion: It is better to encash the US $ after 2 months using forward rates as Rs. 32,43,000 is higher.

Question 6.
The US dollar is selling in India at ₹ 55.50. If the interest rate for a 6 months borrowing in India is 10% per annum and the corresponding rate in USA is 4%.
(i) Do you expect that US dollar will be at a premium or at discount in the Indian FOREX Market?
(ii) What will be the expected 6- month’s forward rate for US dollar in India? And
(iii) What will be the rate of forward premium or discount? [Nov. 2012] [5 Marks]
Answer:
(i) The currency of that country will be at premium where the interest rate is lower as compared to the other country. Therefore, the US dollar is expected to quote at a premium in India.

(it) According to Interest Rate Parity
Forward rate after 6 months = Spot rate $\left[\frac{1+\text { Interest rate in India }}{1+\text { Interest rate in } U S A}\right]^1$
= 55.50 $\left[\frac{1+0.10 / 2}{1+0.04 / 2}\right]^1$ = 55.50 (1.029412) = Rs. 57.13

(iii) Premium Rate (Annualised) = $\frac{57.13-55.50}{55.50} \times \frac{12}{6}$ × 100 = 5.87%

Question 7.
Shoe Company sells to a wholesaler in Germany. The purchase price of a shipment is 50,000 Deutsche Marks with term of 90 days. Upon payment, Shoe company will convert the DM to Dollars. The present spot rate for DM per Dollar is 1.71, whereas the 90-day forward rate is 1.70. (Use Interest-Rate parity Assumption).
You are required to calculate and explain:
(i) If Shoe company were to hedge its foreign exchange risk, what would it do? What transactions are necessary?
(ii) Is the Deutsche Mark at a forward premium or at a forward discount?
(iii) What is the implied differential in interest rates between the two countries?
Answer:
(i) To hedge the foreign exchange risk, shoe company can take forward contract, by selling DM @ 1.70DM/$.
Realization after 90 days: 50,000/1.70 = $ 29,411.76
If the company would not have taken the forward contract it would have faced the risk of depreciation in the value of DM. At spot rate it would have realized 50,000/1.71 = 29239.766.

(ii) The Deutsche Mark is at forward premium. The 90 day forward rate of DM against $ is 1.70 as compared to the present rate of $1.71.

(iii) Under interest rate parity, the difference in interest rate is reflected in the difference in spot and forward rate. This difference is approximately equal to the forward premium or discount. The currency of the country having higher interest rate is traded at discount.
Calculation of forward discount on $.
= $\frac{\text { Forward Rate }- \text { Spot Rate }}{\text { Spot Rate }}$ × 100
= $\frac{1.70-1.71}{1.71}$ × 100
= 0.58479% for 90 days
Annualized Discount = 0.58479 × $\frac{365 \text { days }}{90 \text { days }}$ = 2.3716%
Therefore, the approximate interest difference in the two countries is 2.37% with interest rate in US being higher.

Question 8.
Digital exporters are holding an export bill in United States dollar (USD) 5,00,000 due after 60 days. They are worried about the falling USD value, which is currently at ₹ 75.60 per USD. The concerned Export consignment has been priced on an Exchange rate of ₹ 75.50 per USD. The firm’s Bankers have quoted a 60 day forward rate of ₹ 75.20.
Calculate:
(i) Rate of discount quoted by the bank, assuming 365 days in a year.
(ii) The probable loss of operating profit if the forward sale is agreed to. [Nov. 2018] [5 Marks]
Answer:
The following are the relevant information:
USD Receivables = 5,00,000
Due after 60 days.
₹/$ .
Spot = 75.60
Forward rate = 75.20

(i) Rate of discount quoted by the Bank
= $\frac{F w d .-S p o t}{S p o t}$ × 100
= $\frac{75.20-75.60}{75.60}$ = – 0.529% for 60 days
The negative sign indicates that the US$ is at discount against Rupees.
Annualized = $\frac{0.529}{60}$ × 365 = 3.22% (Approx.)
Loss of operating Profit
(Exchange rate finally received – Exchange Rate for the consignment)
= USD 5,00,000 (75.20 – 75.50)
= ₹ 150,000 (Received-Contracted)

Question 9.
On April 3, 2016, a Bank quotes the following:

Spot Exchange Rate (US $ 1)	NR 66.2525	INR 67.5945
2 months’ swap points	70	90
3 months’ swap points	160	186

In a spot transaction, delivery is made after two days.
Assume spot date as April 5, 2016.
Assume 1 swap point = 0.0001,
You are required to:
(i) Ascertain swap points for 2 months and 15 days. (For June 20, 2016),
(ii) Determine foreign exchange rate for June 20, 2016, and
(iii) Compute the annual rate for premium/discount of US$ on INR, on an average rate. [Nov. 2016] [5 Marks]
Answer:
(i) Ascertainment of Swap points for 2 months and 15 days. (For June 20, 2016),

	Bid	Ask
Swap points for 2 months	70	90
Swap points for 3 months	160	186
Swap points for 30 days	160 – 70 = 90	186 – 90 = 96
By interpolating, Swap points for 15 days after 2 months	90 ÷ 2 = 45	96 ÷ 2 = 48
Swap points for 2 months and 15 days	115 [ 70+ 45]	138 [90+ 48]

(ii) Determination of foreign exchange rate for June 20, 2016, and

Foreign Exchange Rate on 20th June, 2016	66.2640	67.6083
(Original Price + Swap Points)	[66.2525 + 0.0115]	[67.5945 + 0.0138]

(iii) Computation of the annual rate for premium/discount of US$ on INR, on an average rate.

Question 10.
On Sep. 3, 2018, a Bank quotes the following:

Spot Exchange Rate (US $ 1)	INR 66.2525	INR 67.5945
2 months’ swap points	90	80
3 months’ swap points	150	174

In a spot transaction, delivery is made after two days.
Assume spot date as Sep. 5, 2018.
Assume 1 swap point = 0.0001,
You are required to:
(i) Ascertain swap points for 2 months and 15 days. (For Nov. 20, 2018),
(ii) Determine foreign exchange rate for Nov. 20, 2018, and
(iii) Compute the annual rate for premium/discount of US$ on INR, on an average rate.
Answer:
(i) Ascertainment of Swap points for 2 months and 15 days. (For Nov. 20,2018),

	Bid	Ask
Swap points for 2 months	-90	-80
Swap points for 3 months	150	174
Swap points for 30 days	150 – (-90) = 240	174 – (-80) = 254
By interpolating, Swap points for 15 days after 2 months	240÷2 = 120	254÷2 = 127
Swap points for 2 months and 15 days	30 [-90 + 120]	47[-80 + 127]

(ii) Determination of foreign exchange rate for Nov. 20, 2018

Foreign Exchange Rate on 20^th Nov., 2018	66.2555	67.5992
(Original Price + Swap Points)	[66.2525 + 0.0030]	[67.5945 + 0.0047]

(iii) Computation of the annual rate for premium/discount of US$ on INR, on an average rate.

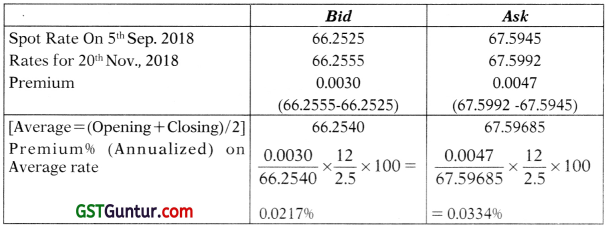
Question 11.
You have following quotes from Bank A and Bank B:

	Bank A	Bank B
SPOT	USD/CHF 1.4650/55	USD/CHF 1.4653/60
3 months	5/10
6 months	10/15
SPOT	GBP/USD 1.7645/60	GBP/USD 1.7640/50
3 months	25/20
6 months	35/25

(i) How much minimum CHF amount you have to pay for 1 Million GBP spot?
(ii) Considering the quotes from Bank A only, for GBP/CHF what are the Implied Swap points for Spot over 3 months. [May 2009] [6 Marks]
Answer:
1. Required: Buy 1 million GBP Spot against CHF using cross currency rates.

2. Action: As the direct quotation for CHF against GBP is not available, First sell CHF against USD and then buy GBP by selling USD. The rates are quoted by two banks i.e. Bank A and Bank B. The transaction will be done with the Bank where it is more profitable.

3. Best alternative: Based on the two cross rates available in the two Banks, trans-action will be done where it is more beneficial. In this case CHF will be converted into USD in Bank A and USD will be converted into GBP in Bank B. (W.N.l)

(W.N.l)
COMPARISON BETWEEN Bank A and Bank B for acquiring USD

(a) USD1 = CHF 1.4650/55	(b) USD1 = CHF 1.4653/60
Ask rate 1.4655	Ask rate 1.4660
Since the USD is less expensive in the Bank A (1.4655 < 1.4660) therefore, USD will be acquired from Bank A
COMPARISON BETWEEN Bank A and Bank B for acquiring GBP
(c) 1GBP = USD 1.7645/60	(d) 1 GBP = USD 1.7640/50
Since the Ask rate for GBP is less in Bank B,(1.7650 < 1.7660) the USD will be sold in Bank B to acquire GBP

(CHF/£)_ask = (CHF/$)_ask × ($/£)_ask
I GBP = 1.4655 × 1.7650
1 GBP = CHF 2.5866
Amount payable for acquiring 1 million GBP will be CHF 2.5866 Million or CHF 25,86,600

(ii) Spot Bid rate GBP 1 = CHF
(CHF/£)_Bid = (CHF/$)_Bid × ($/£)_Bid = 1.4650* 1.7645 = 2.5850
(CHF/£)_ask = (CHF/$)_ask × ($/£)_ask = 1 – 4655* 1.7660 = CHF 2.5881
GBP/USD 3 months swap points are at discount
3 Months forward rate GBP 1 = USD 1.7645-0.0025/1.7660-0.0020
GBP 1 = USD 1.7620/1.7640
USD/CHF 3 months swap points are at premium
3 Months forward rate USD 1 = CHF (1.4650 + 0.0005/1.4655 + 0.0010.) = CHF 1.4655/1.4665
Hence
3 Months forward rate
(CHF/£)_Bid = (CHF/$)_Bid × ($/£)_Bid = 1.4655 × 1.7620 = 2.5822
(CHF/£)_ask = (CHF/$)_ask × ($/£)_ask = 1.4665 × 1.7640 = 2.5869

SPOT (CHF/£)	2.5850/2.5881
3 months	2.5822/2.5869
Swap points	28/12

Question 12.
You have following quotes from Bank A and Bank B:

	Bank A	Bank B
SPOT	USD/FFr.7.50/7.55	USD/FFr.7.49/7.57
3 months	5/10	10/15
6 months	10/15	12/18
SPOT	GBP/USD 1.7645/60	GBP/USD 1.7640/50
3 months	25/20	20/15
6 months	35/25	30/24

Calculate :
(i) How much minimum FFr. amount you have to pay for 1 Million GBP spot?
(ii) Considering the quotes from Bank A only, for GBP/FFr. What are the Implied Swap points for Spot over 6 months.
Answer:
1. Required: Buy 1 million GBP Spot against FFr. using cross currency rates.

2. Action: As the direct quotation for FFr. against GBP is not available, First Buy USD against FFr. and then buy GBP by selling USD. The rates are quoted by two banks i.e. Bank A and Bank B. The transaction will be done with the Bank where it is more profitable.

3. Compare FFr./ USD ask:
Bank A FFr. 7.55
Bank B FFr. 7.57.
Buy USD from Bank A as (7.55 < 7.57)

4. Compare GBP/ USD ask:
Bank A GBP/USD 1.7645/60
Bank B GBP/USD 1.7640/50
Buy GBP from Bank B as (1.7650 < 1.7660)

5. Best alternative: Based on the two cross rates available in the two Banks, transaction will be done where it is more beneficial. In this case FFr. will be converted into USD in Bank A and USD will be converted into GBP in Bank B.
(FFr/£)_ask = (FFr/$)_ask × ($/£)_ask
1 GBP = 7.55 × 1.7650 1 GBP = FFr. 13.32575
Amount payable for acquiring 1 million GBP will be FFr.13.32575 Million

(ii) Spot rate GBP 1 = FFr.:
(FFr./£)_Bid = (FFr./$)_Bid × ($/£)_Bid = 7.50 × 1.7645 = Fr. 13.234
(FFr./£)_ask = (FFr/$)_ask × ($/£)_ask =7.55 × 1.7660 = FFr. 13.333
USD/FFr. 6 months swap points are at premium
6 Months forward rate USD 1 = FFr 7.50 + 0.10/7.55+0.15.
Hence, USD 1= FFr 7.60/7.70
6 Months forward rate GBP/USD
6 months swap points are at discount
6 Months forward rate GBP 1 = USD 1.7645 – 0.0035/1.7660-0.0025
GBP 1 = USD 1.7610/1.7635
Forward rate GBP 1 = FFr.:
(FFr./£)_Bid = (FFr./$)_Bid × ($/£)_Bid = 7.6 × 1.7610 = 13.384
(FFr./£)_ask = (FFr./$)_ask × ($/£)_ask = 7.70 × 1.7635 = 13.579

SPOT (FFr./£)	13.234/13.333
6 months	13.384/13.579
Swap points	150/246

Question 13.
The rate of inflation in USA is likely to be 3% per annum and in India it is likely to be 6.5%. The current spot rate of US $ in India is ? 43.40. Find the expected rate of US $ in India after one year and 3 years from now using purchasing power parity theory. [Nov. 2008, 2017] [4 Marks]
Answer:
Basic information given in the question
The rate of inflation in USA – 396 per annum
The rate of inflation in India – 6.596 per annum
Spot rate 1 USD = Rs. 43.40
According to Purchasing Power Parity
Forward rate after 1 year = Spot rate $\left[\frac{1+\text { Annual Inflation rate in India }}{1+\text { Annual Inflation rate in USA }}\right]^t$
= 43.40$\left[\frac{1+0.065}{1+0.03}\right]^1$ = 43.4 (1.03398) = ₹ 44.875
Forward rate after 3 years = 43.40 $\left[\frac{1+0.065}{1+0.03}\right]^3$ = 43.40 (1.03398)³ = ₹ 47.9762

Question 14.
The rate of inflation in India is 8% per annum and in the U.S.A. it is 4%. The current spot rate for USD in India is ₹ 46. What will be the expected rate after 1 year and after 4 years applying the Purchasing Power Parity theory. [May 2010] [4 Marks]
Answer:
Basic information given in the question
The rate of inflation in USA – 4% per annum
The rate of inflation in India – 8% per annum
Spot rate 1 USD = Rs. 46
According to Purchasing Power Parity
Forward rate after 1 year = Spot rate$\left[\frac{1+\text { Annual Inflation rate in India }}{1+\text { Annual Inflation rate in USA }}\right]^t$
= 46$\left[\frac{1+0.08}{1+0.04}\right]^1$ = 46 (1.03846) = ₹ 47.769
Forward rate after 4 year = 46$\left[\frac{1+0.08}{1+0.04}\right]^4$ = 46 (1.038460)⁴ = ₹ 53.495

Alternative Solution:
The differential inflation is 4%. Hence the rate will keep changing adversely by 4% every year. Assuming that the change is reflected at the

End of Year	₹ × (1 + lnflation Rate)	₹/USD
1	₹ 46.00 × 1.04	47.84
2	₹ 47.84 × 1.04	49.75
3	₹ 49.75 × 1.04	51.74
4	₹ 51.74 × 1.04	53.81

Tutorial Note:
The first alternative is more preferable.

Question 15.
The rate of inflation in India is 10% per annum. What will be the rate of inflation in the U.S.A. if the current spot rate for USD in India is ₹ 48 and the expected rate after 1 year is t 51.26, by applying the Purchasing Power Parity theory.
Answer:
Basic information given in the question
The rate of inflation in USA -?
The rate of inflation in India – 10% per annum
Spot rate 1 USD = ₹ 48
Forward rate after 1 year 1 USD = ₹ 51.26
According to Purchasing Power Parity
Forward rate after 1 year = Spot rate $\left[\frac{1+\text { Annual Inflation rate in India }}{1+\text { Annual Inflation rate in USA }}\right]^t$

The rate of inflation in US is 3% p.a.

Question 16.
The Price of a particular book is ₹ 400 in India, $ 5.50 in USA and £ 4.75 in England.
(a) Determine the exchange rate of $, £ and ₹ if the law of one price holds good, i.e. Purchasing power parity theorem holds good.
(b) If the actual exchange rate is ₹ 70 per USD and ₹ 88 per £, where should
the book be purchased from. [Practice Question]
Answer:
(a)

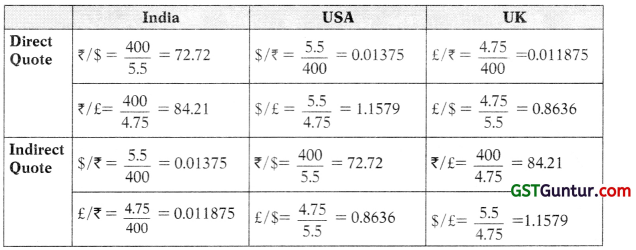
(b) In order to find the place from where the book must be purchased, so that it is most beneficial, can be calculated by finding the price in one common currency, using the exchange rates calculated in part (a) of the solution. Keeping the common currency as ₹ i.e. home currency, the price of the book in ₹:

The Book should be bought in USA, as it is cheapest to buy from there.

Tutorial Note:
The same opinion may be arrived by comparing the exchange rate as per purchasing power parity as calculated in part (a) and those given in the question in part (b) as the US exchange rate is less while in U.K it is higher than calculated in part (a), it will be most beneficial to buy from US.

Question 17.
The Dollar is available in the London Market for £0.7650 i.e. £/$ = 0.7650. If the rates of inflation in the two countries is given as under for the next 4 years, what will be the forward rates for $ if purchasing power parity holds good. Which currency will be at premium in different years taking previous year as base.

Answer:
According to Purchasing Power Parity
Forward rate = Spot rate $\left[\frac{1+\text { Annual Inflation rate in } U K}{1+\text { Annual Inflation rate in } U S A}\right]^t$

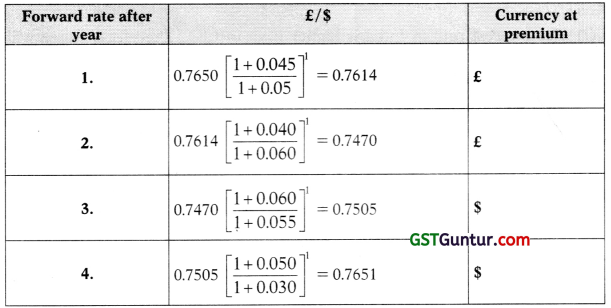
Question 18.
On April 1, 3 months interest rate in the UK £ and US $ are 7.5% and 3.5% per annum respectively. The UK £/US $ spot rate is 0.7570. What would be the forward rate for US $ for delivery on 30th June? [Nov. 2008] [Nov. 2018] [4 Marks]
Answer:
Basic information given in the question
The rate of interest in USA – 3.5% per annum or 0.875% per 3 months
The rate of interest in UK – 7.5% per annum or 1.875% per 3 months
Spot rate 1 US $ = UK £ 0.7570
According to Interest Rate Parity
Forward rate after 3 months = Spot rate$\left[\frac{1+\text { Interest rate in } U K}{1+\text { Interest rate in } U S A}\right]^t$
= 0.7570$\left[\frac{1+0.01875}{1+0.00875}\right]^1$ = 0.7570 (1.009999) = £ 0.7645
Forward rate 1US$ = UK£ 0.7645

Question 19.
If the present interest rate for 6 months borrowings in India is 9% per annum and the corresponding rate in USA is 2% per annum, and the US$ is selling in India at ? 64.50/$.
Then:
(i) Will US$ be at a premium or at a discount in the Indian forward market?
(ii) Find out the expected 6-month forward rate for US$ in India.
(iii) Find out the rate of forward premium/discount. [Nov. 2012 Modified] [Nov. 2017] [5 Marks]
Answer:
(i) The interest rate in India is higher than in USA. Therefore, rupee will depreciate and hence dollar will be at premium.

(ii) According to Interest Rate Parity
The rate of interest in INDIA – 9% per annum or 4.5% per 6 months
The rate of interest in USA – 2% per annum or 1% per 6 months
Spot rate 1 US $ = Rs. 64.50
Forward rate after 6 months = Spot rate $\left[\frac{1+\text { half yearly interest rate in INDIA }}{1+\text { half yearly interest rate in USA }}\right]^t$
= 64.50$\left[\frac{1+0045}{1+0.01}\right]^1$ = 64.50 (1.03465) = Rs. 66.735

(iii) Calculation of forward premium of Dollar.
= $\frac{\text { Forward Rate }- \text { Spot Rate }}{\text { Spot Rate }}$ × 100 $\frac{66.735-64.50}{64.50}$ × 100
= 3.4651% for 6 months
Annualized Premium = 3.4651 × $\frac{12 \text { Months }}{6 \text { Months }}$ = 6.93%

Question 20.
The US Dollar is selling in India at Rs. 72.50. If the interest rate for a 3 months borrowing in India is 6% per annum and the corresponding rate is USA is 2.75%.
(i) Do you expect that US dollar will be at a premium or at discount in the Indian Forex Market ?
(ii) What will be the expected 3-months forward rate for US dollar in India ?
(Hi) What will be the rate of forward premium or discount ? [Nov. 2019 Old Syllabus] [6 Marks]
Answer:
(i) The interest rate in India is higher than in USA. Therefore, rupee will de-preciate and hence dollar will be at premium in the Indian forex market.

(ii) According to Interest Rate Parity
The rate of interest in INDIA – 6% per annum or 1.5% per 3 months
The rate of interest in USA – 2.75% per annum or 0.6875% per 3 months
Spot rate 1 US $ = Rs. 72.50
Forward rate after 3 months = Spot rate
$\left[\frac{1+3 \text { months interest rate in INDIA }}{1+3 \text { months interest rate in USA }}\right]$
= 72.50$\left[\frac{1+0.015}{1+0.006875}\right]^1$ = 72.50 (1.008) = Rs.73.08

(iii) Calculation of forward premium of Dollar.

Question 21.
If the present interest rate for 6 months borrowings in Japan is 6% per annum and the corresponding rate in USA is 2% per annum and the US$ is selling in Japan at JPY128/$.
Then:
(i) Will US$ be at a premium or at a discount in the Japanese forward market?
(ii) Find out the expected 6-month forward rate for US$ In Japan.
(iii) Find out the rate of forward premium/discount on Japanese Yen as well as on US$.
Answer:
(i) The interest rate in Japan is higher than in USA. Therefore, Yen (¥) will depreciate and hence dollar will be at premium.

(ii) According to Interest Rate Parity
The rate of interest in Japan – 6% per annum or 3% per 6 months
The rate of interest in USA – 2% per annum or 1% per 6 months
Spot rate 1 US $ = ¥128
Forward rate after 6 months = Spot rate
$\left[\frac{1+\text { half yearly interest rate in Japan }}{1+\text { half yearly interest rate in USA }}\right]^t$
= 128 $\left[\frac{1+003}{1+0.01}\right]^1$ = 128 (1.0198) = ¥ 130.5344

(iii) Calculation of forward premium on $.

(iv) Calculation of forward Discount on ¥.
= $\frac{\text { Spot Rate-Forward Rate }}{\text { Forward Rate }}$ × 100
= $\frac{128-130.5344}{130.5344}$ × 100
= (-)1.9416 for 6 months
(The negative sign indicates that ¥ is at discount in the forward market.)
Annualized Discount = 1.9416 × $\frac{12 \text { Months }}{6 \text { Months }}$ = 3.8832%

Question 22.
Presently, one US $ is worth 140 Japanese Yen in the spot market. The interest rate in Japan on 90 days Government securities is 4% per annum. If the interest rate parity theorem holds true and 3-month forward rate is 138 Yen per US $, what is the implied interest rate in USA?
If the actual interest rate is 7% per annum in USA, what action would follow?
Answer:
Basic information given in the question
The rate of interest in Japan – 4% per annum or 1.00% for 90 days
Spot rate 1 US $ = JPY 140
Forward rate 1 US $ = JPY 138
According to Interest Rate Parity
Forward rate after 3 months = Spot rate $\left[\frac{1+\text { Interest rate in Japan }}{1+\text { Interest rate in USA }}\right]^t$
130 = 140 $\left[\frac{1+0.01}{1+\text { Interest rate in } U S A}\right]^1$
1 + Interest rate in USA = 140$\left[\frac{1+0.01}{138}\right]^1$
1 + Interest rate in USA = 1.024637
Interest rate in U.K = 1.024637 – 1
= 0.024637
Annualized interest rate = 0.024637 × 4 = 0.09855 = 9.855%
If the actual interest rate in US is 7%, it is below the implied interest as per forward rate, therefore there will be arbitrage opportunity. A person will gain by borrowing in US @ 1%, converting $ into JPY, investing in Japan and reconverting into $ using forward rate.

Question 23.
Mr. Shekhawat has ₹ 1,00,000 to Invest which he can do in India or in US. You are given the following information:

Advise him where should he invest and the net gain by doing so.
Answer:
Basic information given in the question
The rate of interest in USA – 4.5% per annum or 2.25% per 6 months
The rate of interest in India – 6% per annum or 3.00% per 6 months
Spot rate 1 US $ = ₹ 63.00
According to Interest Rate Parity
Forward rate after 6 months = Spot rate $\left[\frac{1+\text { Interest rate in India }}{1+\text { Interest rate in USA }}\right]^t$
= 63.00$\left[\frac{1+0.030}{1+0.0225}\right]^1$ = ₹ 63.46
Since the theoretical forward rate is not equal to the prevailing forward rate, there is an arbitrage opportunity. As the theoretical forward rate is less, Mr. Shekhawat will gain by investing in USA, as $ is expected to appreciate more than influenced bv interest rate.

1. Action	Convert ₹ 1,00,000 into $ at the prevailing rate of ₹ 63. Total $ = $\frac{1,00,000}{63}$ = 1,587.30
2. Invest	Invest in US @ 4.5% p.a. i.e. 2.25% for 6 months
3. Enter into forward contract	Take a forward contract to sell $ @ prevailing forward rate i.e ₹ 63.70.
4. After 6 months	Realize the investment = $1,623.01 (1,587.30 × 1.0225)
5. Convert $ into ₹	1,623.01 × 63.70 = ₹ 1,03,385.74 = ₹ 1,03,386 (as per forward contract)

Had he made the investment in India, he would have got interest @ 3% for 6 months and total value of investment would be ₹ 1,03,000 (₹ 1,00,000 × 1.03). Hence, his net gain is ₹ 386

Question 24.
ABC Ltd. has to make a US$ 5 million payment in three months’ time. The required amount in dollars is available with ABC Ltd. Management of the company decides to invest them for three months and following information is available in this context:

The US$ deposit rate is 9% p.a.	The spot exchange rate is $ 1.82/pound.
The sterling pound deposit rate is 11% p.a.	The 3 month forward rate is $ 1.80/pound.

Answer the following questions:
(i) Where should the company invest for better returns?
(ii) Assuming that the interest rates and the spot exchange rate remain as above, what forward rate would yield an equilibrium situation?
(iii) Assuming that the US interest rate and the spot and forward rates remain as above, where should the company invest if the sterling pound deposit rate were 15% per annum?
(iv) With the originally stated spot and forward rates and the same dollar deposit rate, what is the equilibrium sterling pound deposit rate?
Answer:
Basic information given in the question:
Total $ to be paid $5 million
The rate of interest in UK- 11% per annum or 2.75% per 3 months
The rate of interest in US – 9% per annum or 2.25% per 3 months
Spot rate 1 £ = $1.82
Forward rate 1 £ = $1.80
Asked:

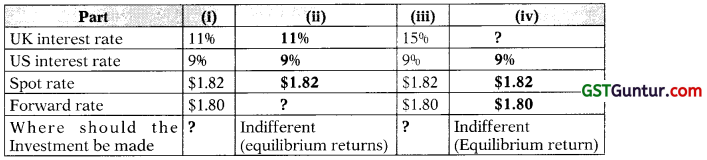
(i) If the investment is made in US:
Receipts after 3 months = 5 million (1.0225) = 51,12,500
Balance left after making the payment = $1,12,500
Convert into £ @ forward rate of 1.80$/ £
= 1,12,500/1.80 = £ 62,500
Alternatively if investment is made in UK
Convert $5 million into £ at the prevailing spot rate = $ 1.82/£
= 50,00,000/1.82 = £ 2747,252.75
Invest in UK for 3 months @11% p.a.
Receipts after 3 months = 27,47,252.75 (1.0275) = £ 28,22,802.20
Use the required £ to convert into $ 5 million at the forward rate of $1.80/£.
=50,00,000/1.80 = £ 27,77,777.78
Balance in hand; = £ 45,024.42 (£ 28,22,802.20 – £ 27,77,777.78)

Therefore, It is better to invest in US
(ii) Equilibrium forward rate:
Forward rate after 3 months = Spot rate $\left[\frac{1+\text { Interest rate in } U S A}{1+\text { Interest rate in } U . K}\right]^t$
= 1.82 $\left[\frac{1+0.0225}{1+0.0275}\right]^1$ = 1.82 (0.99513) = $1.81114
Since the theoretical forward rate is not equal to the prevailing forward rate, there is an arbitrage opportunity. As the theoretical forward rate is more, the investor will gain by investing in USA as £ is expected to depreciate more than influenced by the interest rate. Therefore, the answer in part (i) suggests investment in USA.

(iii) Place of investment, it Pound deposit rate is 15% p.a.
Forward rate after 3 months = Spot rate$\left[\frac{1+\text { Interest rate in } U S A}{1+\text { Interest rate in U.K }}\right]^t$
= 1.82$\left[\frac{1+0.0225}{1+0.0375}\right]^1$ = 1.82 (0.98554) = $ 1.7937
Since the theoretical forward rate is not equal to the prevailing forward rate, there is an arbitrage opportunity. As the theoretical forward rate is less, the investor will gain by investing in UK as £ is expected to depreciate less than influenced by the interest rate.

Verification:
Convert $5 million into £ at the prevailing spot rate = $1.82/£
= 50,00,000/1.82 = £2747,252.75
Invest in UK for 3 months @15% p.a.
Receipts after 3 months = 27,47,252.75(1.0375) =£28,50,274.73
Use the required £ to convert into $ 5 million at the forward rate of $1.80/£.
=50,00,000/1.80 = £27,77,777.78
Balance in hand = £72,496.95 (£28,50,274.73 – £27,77,777.78)
So, it is better to invest in U.K

(iv) Equilibrium Sterling Pound deposit rate:
Forward rate after 3 months = Spot rate $\left[\frac{1+\text { Interest rate in } U S A}{1+\text { Interest rate in } U \cdot K}\right]^t$
1.80 = 1.82 $\left[\frac{1+0.0225}{1+\text { Interest rate in U.K }}\right]^1$
1 + Interest rate in U.K = 1.82 $\left[\frac{1+0.0225}{1.80}\right]^1$
1 + Interest rate in U.K = 1.03386
Interest rate in U.K= 1.03386 – 1 = 0.03386
Annualized interest rate = 0.03386 × 4 =0.13544 = 13.54%

To sum up the answer

Part	Answer
(i)	USA
(ii)	1.81114
(iii)	UK
(iv)	13.54%

Question 25.
The following table shows interest rates for the United states dollar and French francs (FFr.). The spot exchange rate is 7.05 francs per dollar. Complete the missing figures:

Answer:
Basic information given in the question
The rate of interest in US- 11.5% per annum or 2.875% per 3 months
The rate of interest in France – 19.5% per annum or 4.875% per 3 months
Spot rate 1 USD = FF_r7.05

According to Interest Rate Parity
1. Missing value for 3 months period:
(i) Forward rate after 3 months = Spot rate $\left[\frac{1+\text { Interest rate in France }}{1+\text { Interest rate in } U S A}\right]^t$
= 7.05 $\left[\frac{1+004875}{1+0.02875}\right]^1$ = 7.05 (1.01944) = FF_r7.18705

(ii) Calculation of forward Discount on FFr.
= $\frac{\text { Spot Rate }- \text { Forward Rate }}{\text { Forward Rate }}$ × 100 = $\frac{7.05-7.18705}{7.18705}$ × 100
= (-) 1.9069 for 3 months
(The negative sign indicates that FFr is at discount in the forward market.)
Annualized Discount = 1.9069 × $\frac{12 \text { Months }}{3 \text { Months }}$ = 7.627%

2. Missing value for 6 months period
(i) Calculation of Franc interest and Forward rate after 6 months

(The negative sign indicates that FF_r is at discount in the forward market.)
Solving for x
Forward rate = 7.28FFr

(ii) Interest rate in France
7.28 = 7.05$\left[\frac{1+\text { Interest rate in France }}{1.06125}\right]^t$
= 0.09587 = 9.587% for 6 months
Annualized = 19.17% (9.587 × $\frac{12}{6}$)

3. Missing value for 1 year period
(i) Calculation of interest in US:
Forward rate after 1 year = Spot rate $\left[\frac{1+\text { Interest rate in France }}{1+\text { Interest rate in } U S A}\right]^t$
FF_r 7.52 = 7.05$\left[\frac{1+0.20}{1+x}\right]^1$
Solving for x
1 + x = 1.125
x = 0.125 = 12.5%
Therefore annual interest in US = 12.5%

(ii) Calculation of forward Discount on FFr.
= $\frac{\text { Spot Rate }- \text { Forward Rate }}{\text { Forward Rate }}$ × 100 = $\frac{7.05-7.52}{7.52}$ × 100
= 6.25%

Question 26.
ABC Ltd. of UK has exported goods worth Singapore $ (S$) 1,00,000 receivable in 6 months. The exporter wants to hedge the receipt in the forward market. The following information is available:

Spot Exchange Rate (S$/£)	3.60
Interest Rate in UK	6%
Interest Rate in Singapore	15%

The forward rates truly reflect the interest rates differential. Find out the gain/loss to UK exporter if S $ spot rates (i) declines 2%, (ii) gains 4% or (iii) remains unchanged over next 6 months. [Practice Question]
Answer:
According to Interest Rate Parity
Forward rate after 6 months = Spot rate $\left[\frac{1+\text { Interest rate in Singapore }}{1+\text { Interest rate in } U K}\right]^t$
Forward Rate = $\frac{3.60(1+0.075)}{(1+0.030)}$ = S$ 3.7573/£

(i) If Singapore $ (S$) spot rate decline by 2% then, the rate will be
$\frac{1}{3.6}$ × 0.98 = $\frac{0.2722 £}{\text { S. } \$}$ = S $ $\frac{0.2722 £}{\text { S. } \$}$ /£ = S$ 3.6735/£

	£
£ receipt as per Forward Rate (SS 1,00,000/3.7573) (Rounded off)	26,615
£ receipt as per Spot Rate after the decline (S$ 1,00,000/3.6735)	27,222
Loss due to forward contract	607

Since the forward price implies a higher rate of decline in rates, there will be loss in taking forward cover.

(ii) If S$ spot rate gains by 4% then the rate will be
$\frac{1}{3.6}$ × 1.04 = $\frac{0.2889 £}{\mathrm{~S} \$}$ = S$ $\frac{1}{0.2889}$/£ = S$ 3.4614/£

	£
£ receipt as per Forward Rate (S$ 1,00,000/3.7573)	26,615
£ receipt as per Spot Rate (S$ 1,00,000/3.4614)	28,890
Loss due to forward contract	2,275

(iii) If spot rate remains unchanged

	£
£ receipt as per Forward Rate (S$ 1,00,000/3.7573)	26,615
£ receipt as per Spot Rate (S$ 1,00,000/3.6)	27,778
Loss due to forward contract	1,163

Question 27.
An Indian company obtains the following quotes (₹/$)

Spot:	35.90/36.10
3-months forward rate:	36.00/36.25
6-months forward rate:	36.10/36.40

The company needs $ funds for six months. Determine whether the company should borrow in $ or ₹.
Interest rates are:
3-months interest rate: ₹ : 12%; $: 6%
6-months interest rate: ₹ : 11.50%; $:5.5%
Also determine what should be the rate of interest after 3-months to make the company indifferent between 3-month borrowing and 6-months borrowing in the case of:
(i) Rupee borrowing
(ii) Dollar borrowing
Note: For the purpose of calculation, you can take the units of dollar and rupee as 100 each. [Nov. 2018] [8 Marks]
Answer:
The following information is given
Spot Rate $\left(\frac{₹}{\$}\right)$ = 35.90/36.10
3 months forward rate: 36.00/36.25
6 months forward rate: 36.10/36.40
3 months interest rate: ₹ 12%/$6%
6 months interest rate: ₹ 11.50%/$5.5%
The Company needs to Borrow $ for 6 months.
If the Company Borrows in $ [Let us assume it needs $ 100]
Borrow = 100 $ @ 5.5%
Repay = 100 $ after 6 months together with interest
6 Months interest = 100 × $\frac{5.5}{100}$ × $\frac{6}{12}$ =$2.75
Total outflow = Principal ($ 100) + Int. ($ 2.75) = $ 102.75
Amount in ₹ required to repay the loan taken in dollars
= 102.75 × 6 months forward ask rate
= 102.75 × 36.40 = ₹ 3,740.10
If the Indian Company borrows in Rupees, equivalent to $ 100
Rupees required to buy 100 $ in Spot market = 100 × 36.10 = ₹ 3,610
Rate of interest for 6 months borrowing in ₹ = 11.5096 p.a. i.e. 5.75% for 6 months.
Interest on loan (₹ 3,610 × 5.7596) = ₹ 207.5.75
Total Outflow in ₹ (Principal + Interest) = ₹ 3,610 + ₹ 207.575
= 3,817.575 or ₹ 3817.60 app.

Conclusion: Since the outflow is less if money is borrowed in $, therefore the Company should make the borrowings in $ only.

Determination of Forward Rate of Interest [3 months after 3 months]
The rate of interest after 3 months to as to make the Company indifferent between 3 months borrowing and 6 months borrowing shall be the 3 months forward rate of interest after 3 months.

(i) In case of Rupee borrowing
3 months interest rate = 12% p.a.
Rate of Interest for 3 months = 12/4 = 3% or 0.03
6 months interest rate = 11.50% p.a.
Rate of interest for 6 months = 5.75% p.a.
∴ 3 months forward rate (f):
= (1.03) (1 + f) = 1.0575
(1 + f) = $\frac{1.0575}{1.03}$ = 1.0267
Rate = (1.0267 – 1) × 100 = 2.67%
∴ 3 month interest after 3 months in Rupee = 2.67%
Annualized = 2.67 × 4 = 10.68%

(ii) In case of Dollar borrowing
3 month interest rate = 6% p.a.
6 months interest rate = 5.5% p.a
(1.015) (1 + f) = 1.0275
(1 + f) = 1.01231
Forward rate = (1.01231 – 1) × 100 = 1.23%
Annualized = 1.23 × 4 = 4.9296

Question 28.
Your FOREX dealer had entered into a cross currency deal and had sold US $ 10,00,000 against EURO at US $ 1 = EURO 1.4400 for spot delivery.
However, later during the day, the market became volatile and the dealer in compliance with his management’s guidelines had to square-up the position when the quotations were:

Spot US $ 1	INR 31.4300/4500
1 month margin	25/20
2 months margin	45/35
Spot US $ 1	Euro 1.4400/4450
1 month forward	1.4425/4490
2 months forward	1.4460/4530

What will be the gain or loss in the transaction? [May 2009] [6 Marks]
Answer:

1. Exposure	US $ 10,00,000 sold against Euros. EURO Receivables 10,00,000 × 1.4400 = EURO 14,40,000
2. Action	Square off Position i.e. Buy US $ 10,00,000 Spot US $ 1 = Euro 1.4400/4450 EURO Payables 10,00,000 × 1.4450 = EURO 14,45,000
3. Net position	Net Loss in the Transaction = EURO 5,000
4. Convert loss into Rs.	As the direct quotation for Rupee against Euro is not available, Cross currency Ask rate for Euro is required to be calculated.

Given:
(a) USD 1 = EURO 1.4400/4450
(b) USD 1 = INR 31.4300/4500
Cross Currency ask rate of 1EURO =

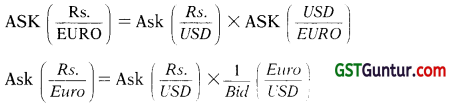
Rs. 31.4500/1.440 i.e. Rs. 21.8403
Loss in the Transaction to acquire EURO 5,000 from the market Rs. 21.8403 × 5,000 = Rs. 1,09,201.50

Question 29.
A Bank sold Hong Kong Dollars 40,00,000 value spot to its customer at ₹ 7.15 and covered itself in London Market on the same day, when the exchange rates were :
U$$ 1 = HK$ 7.9250/7.9290
Local inter-bank market rates for US$ were
Spot US$ 1 = ₹ 55.00/55.20
You are required to calculate rate and ascertain the gain or loss in the transaction. Ignore brokerage.
You have to show the calculations for exchange rate up to four decimal points. [May 2013] [5 Marks]
Answer:

1. Exposure	HK $ 40,00,000 sold against Rupees Rupees Receivables 40,00,000 × 7.15 = RS. 2,86,00,000
2. Action	Cover Position i.e. Buy HK $ 40,00,000 Payables 40,00,000 × 6.9653 (WN) = RS. 2,78,61,200
3. Determine Ask rate of HK$ against rupee	As the direct quotation for HK$ against Rupee is not available, Cross currency Ask rate for HK$ is required to be calculated.
4. Net position	Net gain in the Transaction = Rs. 7,38,800

Working Note:
To acquire HK$40,00,000 from the market
(a) US$ 1 = HK$ 7.9250/7.9290 (London Market)
(b) USD 1 = INR Rs. 55.00/55.20 (Local Market)

Cross Currency buying rate of 1HKS =
Rs.55.20/7.9250 i.e. Rs.6.9653
Payables 40,00,000 × 6.9653 = ₹ 27,861,200
Gain in the Transaction Rs. (2,86,00,000 – 2,78,61,200) = Rs. 7,38,800
Alternatively :
Gain in the Transaction = 40,00,000 (₹ 7.15 – ₹ 6.9653) = ₹ 7,38,800

Question 30.
Edelweiss Bank Ltd. sold Hong Kong dollar 2 crores value spot to its customer at ₹ 8.025 and covered itself in the London market on the same day, when the exchange rates were
US $ 1 = HK $ 7.5880 – 7.5920
Local inter-bank market rates for US $ were
Spot US $ 1 = ₹ 60.70 – 61.00
Calculate the cover rate and ascertain the profit or loss on the transaction. Ignore brokerage. [May 2014] [Nov. 2014] [5 Marks]
Answer:

Exposure	HK $ 2,00,00,000 sold against Rupees Rupees Receivables 2,00,00,000 × 8.025 = Rs. 16,05,00,000
Action	Cover Position i.e. Buy HK $ 2,00,00,000 Payables 2,00,00,000 × 8.039(WN)= Rs. 16,07,80,000
Determine Ask rate of HK$ against rupee	As the direct quotation for HK$ against Rupee is not available, Cross currency Ask rate for HK$ is required to be calculated.
Net position	Net Loss in the Transaction = Rs. 2,80,000

Working Note:
To acquire HK$2,00,00,000 from the market
(a) US$ 1 = HK$ 7.5880 – 7.5920
(b) USD 1 = ₹ 60.70 – 61.00 (Local Market)

Cross Currency buying rate of 1 HK$ = INR
Rs. 61.00/7.5880 i.e. Rs. 8.0390
Payables 2,0000000 × 8.039 = 16,07,80,000
Loss in the Transaction Rs. (16,05,00,000 – 16,07,80,000) = Rs. 2,80,000
Alternatively:
Loss in the Transaction = 2,00,00,000 (₹ 8.025 – ₹ 8.039) = ₹ 2,80,000

Question 31.
The Bank sold Hong Kong Dollar 1,00,000 spot to its customer at ₹ 7.5681 and covered itself in London market on the same day, when the ex-change rates were
US $ 1 = HK $ 8.4409 HK $ 8.4500
Local inter-bank market rates for US $ were:
Spot US 1 = ₹ 62.7128 ₹ 62.9624
Calculate the cover rate and ascertain the profit or loss in the transaction. [May 2014] [5 Marks]
Answer:

1. Exposure	HK $ 1,00,000 sold against Rupees Rupees Receivables 1,00,000 × 7.5681 = Rs. 7,56,810
2. Action	Cover Position i.e. Buy HK $ 1,00,000 Payables 1,00,000 × 7.4592(WN) = RS. 7,45,920
3. Determine Ask rate of HK$ against rupee	As the direct quotation for HK$ against Rupee is not available, Cross currency Ask rate for HK$ is required to be calculated.
4. Net position	Net gain in the Transaction = Rs. 10,890

Working Note:
To acquire HK$1,00,000 from the market
(a) USD 1 = HK $ 8.4409/8.4500 (London Market)
(b) USD 1 = ₹ 62.7128/62.9624 (Local Market)
Cross Currency buying rate of 1HK$ =

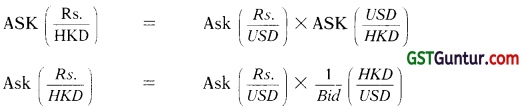
Rs. 62.9624/8.4409 i.e. Rs. 7.4592
Payables = 7.4592 × 1,00.000 = ₹ 7,45,920
Gain in the Transaction Rs. (7,56,810 – 7,45,920) = Rs. 10,890

Alternatively:
Gain in the Transaction = 1,00,000 (₹ 7.5681 – ₹ 7.4592) = ₹ 10,890

Question 32.
You as a forex dealer had entered into a cross currency deal and had sold US $ 10,000 against GBP at US $ 1 = GBP 0.7650 for spot delivery.
However, the management has ordered immediate cancellation of the same considering the increased volatility in the market.

Spot US $ 1	INR 68.2500/4500
1 month margin	15/20
2 months margin	45/70
Spot US $ 1	GBP 0.7650/0.7720
1 month forward points	20/35
2 months forward points	35/25

What will be the gain or loss in the transaction?
Answer:

1. Exposure	US $ 10,000 sold against GBP. GBP Receivables 10,000 × 0.7650 = £ 7,650
2. Action	Square off Position i.e Buy US $ 10,000 Spot US $ 1 = GBP 0.7650/0.7720 £ Payables 10,000 × 0.7720 = £ 7720
3. Net position	Net Loss in the Transaction = £70
4. Convert loss into ₹	As the direct quotation for Rupee against £ is not available, Cross currency Ask rate for £ is required to be calculated.

The spot rates available are:
(£/$) bid = £0.7650
(£/$) ask = £0.7720
(₹/$) bid = ₹ 68.25
(₹/$) ask = ₹ 68.45
From above available rates we can compute required rate as follows:
(₹/£)_ask = ($/£)_ask × (₹/$)_ask
$\left(\frac{1}{£ / \$}\right)_{\text {bid }}$ × (₹/$)_ask
= (1/0.7650) × (68.45) = ₹ 89.4771
Total Loss = ₹ 6,263 (89.4771 × 70)

Question 33.
You, a foreign exchange dealer of your bank, are informed that your bank has sold a T.T. on Copenhagen for Danish Kroner 10,00,000 at the rate of Danish Kroner 1 = ₹ 6.5150. You are required to cover the transaction either in London or New York market. The rates on that date are as under:

Mumbai – London	₹ 74.3000	₹ 74.3200
Mumbai- New York	₹ 49.2500	₹ 49.2625
London – Copenhagen	DKK 11.4200	DKK 11.4350
New York – Copenhagen	DKK 07.5670	DKK 07.5840

In which market will you cover the transaction, London or New York, and what will be the exchange profit or loss on the transaction? Ignore brokerages. [Nov. 2013] [5 Marks]
Answer:

1. Exposure	Danish Kroner DKK 10,00,000 sold against Rupees Rupees Receivables 10,00,000 × 6.5150 = Rs. 65,15,000
2. Action	Cover Position Le. Buy DKK 10,00,000 Option 1 (London Market) Payables 10,00,000 × 6.5079(WN 1) = Rs. 65,07,880 Option 2 (New York Market) Payables 10,00,000 × 6.51017(WN 2) = Rs. 65,10,170
3. Determine Ask rate of DKK against rupee	As the direct quotation for DKK against Rupee is not available, Cross currency Ask rate for DKK is required to be calculated. It is available both in the London Market and in the New York Market.
4. Option	Based on the two cross rates available in the two markets, transaction will be done where it is more beneficial. In this case it will be done through London Market.
5. Net position	Net gain in the Transaction = Rs. 7,120 (65,15,000 – 65,07,880

Comparison Between London Market And New York Market

To acquire DKK 10,00,000 from the London market	To acquire DKK 10,00,000 from the New York market
(a) GBP1 = DKK 11.4200/11.4350 (London Market)	(a) USD1 = DKK 7.5670/7.5840 (London Market
(b) GBP 1 = ₹ 74.3000/74.3200(Mumbai Market) Cross Currency buying rate of DKK = 74.3200/11.4200 i.e. Rs 6.50788 Gain in the Transaction Rs. (65,15,000 – 65,07,880) = Rs. 7,120	(b) USD 1 = ₹ 49.2500/49.2625 (Mumbai Market) Cross Currency buying rate of DKK = Rs. 49.2625/7.567 i.e. Rs 6.51017 Gain in the Transaction Rs. (65,15,000 – 65,10,170) = Rs. 4830
Alternatively:
Gain in the Transaction = 10,00,000 (6.5150 – 6.50788) = ₹ 7,120	Gain in the Transaction = 10,00,000 (6.5150 – 6.51017) = ₹ 4,830
Therefore, it is better to buy from London Market.

Question 34.
You, a foreign exchange dealer of your bank, are informed that your bank has sold a T.T. on Swiss Francs 1,00,000 (CHF) at the rate of CHF 1 = ₹ 15.65. You are required to cover the transaction either in London or New York market. The rates on that date are as under:

Mumbai – London	₹ 85.40	₹ 85.65
Mumbai- New York	₹ 65.25	₹ 65.45
London – Switzerland	CHF5.80	CHF5.90
New York – Switzerland	CHF4.50	CHF 4.75

In which market will you cover the transaction, London or New York, and what will be the exchange profit or loss on the transaction? [Practice Question]
Answer:

1. Exposure	CHF 1,00,000 sold against Rupees Rupees Receivables 1,00,000 × 15.65 = Rs. 15,65,000
2. Action	Cover Position i.e Buy CHF 1,00,000 Option 1 (London Market) Payables 1,00,000 × 14.7672(WN 1) = Rs. 14,76,720 Option 2 (New York Market) Payables 1,00,000 × 14.544 (WN 1) = Rs. 14,54,444
3. Determine Ask rate of CHF against rupee	As the direct quotation for CHF against Rupee is not available, Cross currency Ask rate for CHF is required to be calculated. It is available both in the London Market and in the New York Market.
4. Option	Based on the two cross rates available in the two markets, transaction will be done where it is more beneficial. In this case it will be done through New York Market.
5. Net position	Net gain in the Transaction = ₹ 1,10,560 (15,65,000 -14,54,440)

Working Note -1 (W.N. 1)
Comparison Between London Market and New York Market

To acquire CHF 1,00,000 from the London market	To acquire CHF 1,00,000 from the New York market
(a) GBP1 = CHF 5.80/5.90 (London Market) (b) GBP 1 = ₹ 85.40/85.65 (Mumbai Market) = $\frac{\text { Cross Currency Ask rate of CHF }}{85.65 / 5.80 \text { i.e. Rs. } 14.7672}$ Gain in the Transaction ₹ (15,65,GOO – 14,76,720) = ₹ 88,280	(a) USD1 = CHF 4.50/4.75 (London Market) (b) USD 1 = ₹ 65.25’65.45 (Mumbai Market) = $\frac{\text { Cross Currency Ask rate of CHF }}{\text { Rs. } 65.45+.50 \mathrm{icc} \text { Rs. } 14.5444} $ Gain in the Transaction ₹ (15,65,000 – 14,54,440) = ₹ 1,10,560
Alternatively:
Gain in the Transaction = 1,00,000 (15.6514.7672) = ₹ 88280	Gain in the Transaction = 1,00,000 (15.65 . 14.5444) = ₹ 1,10,560
Therefore, it is better to cover the transaction in New York Market.

Question 35.
An Indian importer has to settle an import bill for $ 1,30,000. The exporter has given the Indian exporter two options.
(i) Pay immediately without any interest charges.
(ii) Pay after three months with interest at 5 per cent per annum.
The importer’s bank charges 15 per cent per annum on overdrafts. The ex-change rates in the market are as follows :
Spot rate (₹/$): 48.35/48.36
3-Months forward rate (₹/$): 48.81/48.83
The importer seeks your advice. Give your advice. [Nov. 2011] [6 Marks]
Answer:
Alternative I: To pay immediately without interest to the supplier
He will borrow the required amount from his bank @ 15%. The applicable Spot Rate is (₹/$) 48.35/48.36. Accordingly, the outflow under this option after 3 months will be the overdraft amount together with interest

	₹
Amount required to purchases $ 1,30,000 [$ 1,30,000 × ₹ 48.36]	62,86,800
Add: Overdraft Interest for 3 months @ 15% p.a.	2,35,755
	65,22,555

Alternative II: To pay after 3 months together with 5% interest to the supplier
Amount Payable = Invoice Amount + Interest for 3 months @ 5% p.a.
= $ 1,30,000 + ($ 1,30,000 × 5% × 3/12) = $ 1,31,625
Accordingly, he will have to buy $ in forward market. The applicable Forward Rate is (₹/$) 48.81/48.83. Accordingly, the outflow under this option after 3 months will be
Outflow = US$ 131625 × 48.83 = ₹ 64,27,249
Since outflow of cash is less in second alternative, the importer should pay the supplier after 3 months together with 5% p.a.

Question 36.
Z Ltd. importing goods worth USD 2 million, requires 90 days to make the payment. The overseas supplier has offered a 60 days interest free credit period and for additional credit for 30 days and interest of 8% per annum. The bankers of Z Ltd. offer a 30 days loan at 10% per annum and their quote for foreign exchange is as follows:

	₹
Spot 1 USD	56.50
60 days forward for 1 USD	57.10
90 days forward for 1 USD	57.50

You are required to evaluate the following options :
(i) Pay the supplier in 60 days, or
(ii) Avail the supplier’s offer of 90 days credit. [Nov. 2012] [8 Marks]
Answer:
I: To pay in 60 days without interest to the supplier
He will borrow the required amount from his bank @ 10%. The applicable Forward Rate is (₹/$) 57.10. Accordingly, the outflow under this option after 90 4ays will be overdraft amount + interest

	₹
Amount required to purchases $ 20,00,000 [$ 20,00,000 × ₹ 57.10]	11,42,00,000
Add: Overdraft Interest for 30 days @ 10% p.a.	9,51,667
	11,51,51,667

II: To pay after 30 days after the interest free credit period together with 8% interest to the supplier
Amount Payable = Invoice Amount + Interest for 30 days @ 8% p.a.
= $ 20,00,000 + ($ 20,00,000 × 8% × 1/12) = $ 20,13,333
Accordingly, he will have to buy $ in forward market. The applicable Forward Rate is (₹/$) 57.50. Accordingly, the outflow under this option after 30 davs will be Outflow = US$ 20,13,333 × 57.50 = ₹ 11,57,66,648
Since outflow of cash is less in first alternative, the importer should pay the supplier after 60 days by borrowing from the bank.

Question 37.
Gibralter Limited has imported 5,000 bottles of shampoo at landed cost in Mumbai, of US $ 20 each. The company has the choice for paying for the goods immediately or in 3 months time. It has a clean overdraft limit where 14% p.a. rate of interest is charged.
Calculate which of the following method would be cheaper to Gibralter Limited.
(i) Pay in 3 months time with interest @ 10% and cover risk forward for 3 months.
(ii) Settle now at a current spot rate and pay interest of the overdraft for 3 months.
The rates are as follow:
Mumbai ₹/$ spot: 60.25 – 60.55
3 months swap: 35/25 [Nov. 2014] [8 Marks]
Answer:
Alternative I: To pay after 3 months together with 10% interest to the supplier
Amount Payable = Invoice Amount + Interest for 3 months @10% p.a.
= $ 1,00,000 + ($ 1,00,000 × 10% × 3/12) = $ 1,02,500
Accordingly, he will have to buy $ in forward market. The applicable Forward Rate is Mumbai ₹/$ spot: 60.25 – 60.55
3 months swap: 35/25
Therefore Forward rate is = 59.90/60.30 since the swap points are decreasing therefore $ is at discount and swap points should be deducted from spot rates. Accordingly, the outflow under this option after 3 months will be Outflow = US$ 1,02,500 × 60.30 = ₹ 61,80,750
Alternative II: To pay immediately without interest to the supplier
He will borrow the required amount from his bank @ 14%. The applicable Spot Rate is (₹/$): 60.25 – 60.55
Accordingly, the outflow under this option after 3 months will be

	₹
Amount required to purchases $ 1,00,000 [ $ 1,00,000 × ₹ 60.55]	60,55,000
Add: Overdraft Interest for 3 months @ 14% p.a.	211,925
	62,66,925

Since outflow of cash is less in first alternative, the importer should pay the supplier after 3 months together with 10% p.a.

Question 38.
DEF Ltd. has imported goods to the extent of US$ 1 crore. The payment terms are 60 days interest-free credit. For additional credit of 30 days, interest at the rate of 7.75% p.a. will be charged.
The banker of DEF Ltd. has offered a 30 days loan at the rate of 9.5% p.a. Their quote for the foreign exchange is as follows :

Spot rate INR/US$	62.50
60 days forward rate INR/US$	63.15
90 days forward rate INR/US$	63.45

Which one of the following options would be better?
(i) Pay the supplier on 60th day and avail bank loan for 30 days
(ii) Avail the supplier’s offer of 90 days credit [May 2015] [5 Marks]
Answer:
I: To pay in 60 days without interest to the supplier
He will borrow the required amount from his bank @ 9.5%. The applicable Forward Rate is (₹/$) 63.15. Accordingly, the outflow under this option after 30 days will be

	₹
Amount required to purchases $ 1,00,00,000 [$ 1,00,00,000 × ₹ 63.15]	63,15,00,000
Add: Overdraft Interest for 30 days @ 9.5% p.a.	49,99,375
	63,64,99,375

II: To pay after 30 days together with 7.75% interest to the supplier
Amount Payable = Invoice Amount + Interest for 30 days @ 7.75% p.a.
= $ 1,00,00,000 + ($ 1,00,00,000 × 7.75% × 1/12) = $ 1,00,64583.33
Accordingly, he will have to buy $ in forward market. The applicable Forward Rate is (₹/$). 63.45, the outflow under this option after 30 days will be
Outflow = US$ 1,00,64,583.33 × 63.45 = ₹ 63,85,97,812. Since outflow of cash is less in first alternative, the importer should pay the supplier after 60 days by borrowing from the bank.

Question 39.
An Indian importer has to settle an import bill for $ 2,50,000.
The exporter has given the Indian exporter two options.
(i) Pay immediately without any interest charges.
(ii) Pay after three months with interest at 6 per cent per annum.
The importer’s bank charges 15 per cent per annum on overdrafts. The exchange rates in the market are as follows:
Spot rate (Rs./$) :65.28/65.82 3-Months forward rate (Rs./$) :66.10/66.85
The importer seeks your advice. Give your advice. [Practice Question]
Answer:
Alternative I: To pay immediately without interest to the supplier
He will borrow the required amount from his bank @ 15%. The applicable Spot Rate is (₹/$) 65.28/65.82. Accordingly, the outflow under this option after 3 months will be:

	₹
Amount required to purchases $ 2,50,000 [$ 2,50,000 × ₹ 65.82]	1,64,55,000
Add: Overdraft Interest for 3 months @ 15% p.a.	6,17,063
	1,70,72063

Alternative II: To pay after 3 months together with 5% interest to the supplier
Amount Payable = Invoice Amount + Interest for 3 months @ 6% p.a.
= $ 2,50,000 + ($ 2,50,000 × 6% × 3/12) = $ 2,53,750
Accordingly, he will have to buy $ in forward market. The applicable Forward Rate is (/$) ask is 66.85. Accordingly, the outflow under this option after 3 months will be
Outflow = US$ 2,53,750 × 66.85 = ₹ 1,69,63,188
Since outflow of cash is less in second alternative, the importer should pay the supplier after 3 months together with interest @ 6% p.a.
Note: The amount in Rupee has been rounded of in multiples of 1 rupee wherever fraction arose.

Question 40.
An exporter is a UK based company. Invoice amount is $ 3,50,000. Credit period is three months. Exchange rates in London are:

Spot Rate	($/£) 1.5865 – 1.5905
3-month Forward Rate	($/£) 1.6100-1.6140

Rates of Interest in Money Market:

	Deposit	Loan
$	7%	9%
£	5%	8%

Compute and show how a money market hedge can be put in place. Compare and contrast the outcome with a forward contract. [Nov. 2008] [6 Marks]
Answer:
Money Market Hedge:
Since the UK exporter has $ 3,50,000 receivable after 3 months, he must create an opposite situation where he has exactly $ 3,50,000 payables after 3 months. This can be done by borrowing the present value of $ 3,50,000 as per the borrowing rates applicable in US, which is 9% p.a.
Exposure and action to be taken Today

Asset	$ 3,50,000 receivables after 3 months
Create	$ 3,50,000 liability after 3 months
Borrow	Present Value of $ 3,50,000 at 9% for 3 months = $\frac{\$ 3,50,000}{1.0225}$ = $ 3,42,299
Convert into £	Indirect Quote is ($/£) 1.5865 – 1.5905 Conversion Value = $\frac{\$ 3,42,299}{1.5905}$ = £ 2,15,214.71
Invest	£2,15,214.71 (a deposit rate in L K i.e. 54 p.a.

Situation after 3 months

Receive	$ 3,50,000
Repay Loan with Int.	$ 3,42,299 + $ 77,701 = $ 3,50,000
Realise the Investment	£2,15,214.71 × 1.0125 = £ 2,17,904.89
Final Inflow in £	£ 2,17,904.89

Forward Contract:
Using forward rate, amount receivable is = 3,50,000/1.6140 = £ 2,16,852.54
Calculation of money market hedge gain/loss:
Since inflow in money market hedge is higher, therefore money market hedge should be used as a technique for hedging.
Amount received through money market hedge = £2,17, 904.45
Using forward rate, amount receivable is = 3,50,000/1.6140 = £ 2,16,852.54
Gain = 2,17,904.45 – 2,16,852.54 = £ 1,051.91
So, money market hedge is beneficial for the exporter.

Question 41.
H Ltd. is an Indian firm exporting handicrafts to North America. All the exports are invoiced in US$. The firm is considering the use of money market or forward market to cover the receivable of $50,000 expected to be realized in 3 months time and has the following information from its banker:

	Exchange Rates
Spot	Rs./$ 72.65/73
3-m forward	Rs./$ 72.95/73.40

The borrowing rates in US and India are 6% and 12% p.a. and the deposit rates are 4% and 9% p.a. respectively.
(i) Which option is better for H Ltd ?
(ii) Assume that H Ltd. anticipates the spot exchange rate in 3-months time to be equal to the current 3-months forward rate. After 3-months the spot exchange rate turned out to be Rs/$ : 73/73.42. What is the foreign exchange exposure and risk of H Ltd ? [Nov. 2019 Old Syllabus] [8 Marks]
Answer:
Money Market Hedge:
Since H Ltd., the exporter has $ 50,000 receivable after 3 months, he must create an opposite situation where he has exactly S 50,000 payables after 3 months. This can be done by borrowing the present value of S 50,000 as per the borrowing rates applicable in US, which is 6% p.a.

Exposure and action to be taken Today
Asset	$ 50,000 receivables after 3 months
Create	$ 50,000 liability after 3 months
Borrow	Present Value of $ 50,000 at 6% for 3 months = $\frac{\$ 50,000}{1.015}$ ⁼$ 49,261.08 i.e. Approx. = $49261
Convert into Rs.	Direct Quote 72.65 73 Conversion Value = $ 49261 × 72.65 = Rs. 35,78811.65 = Rs. 35,78,812
Invest	Rs. 35,78,812 (a deposit rate in India 9% i.e. p.a.
Situation after 3 months
Receive	$ 50,000
Repay Loan with Int.	$ 49261 + 738.91 – $49,999.91 i.e. Approx. $50,000
Realise the Investment	Rs. 35,78,812 × 1.0225 = Rs. 36,59,335
Final Inflow in £	Rs. 36,59,335

Forward Contract:
Using forward rate, amount receivable is = $ 50,000 × 72.95 = Rs. 36,47,500
(i) Calculation of money market hedge gain /loss:
Since inflow in money market hedge is higher, therefore, money market hedge should be used as a technique for hedging.
Amount received through money market hedge = Rs.36,59,335
Using forward rate, amount receivable is = Rs.36,47,500
Gain = 36,59,335 – 36,47,500 = Rs. 11,835
So, money market hedge is beneficial for the exporter.

(ii) If after 3 months exchange rate turns out to be Rs./S : 73/74.42 his exposure is = 50,000 × 73 = Rs. 36,50,000.

Question 42.
An Indian exporting firm, Rohit and Bros, would like to cover itself against a likely depreciation of pound sterling. The following data is given:
Receivables of Rohit and Bros : £ 5,00,000
Spot rate : ₹ 56.00/£
Payment date: 3-months
3-months interest rate : India : 12 per cent per annum
UK : 5 per cent per annum
What should the exporter do? [Nov. 2008] [6 Marks]
Answer:
Money Market Hedge :
Since the Indian exporter has £ 5,00,000 receivable after 3 months, he must create an opposite situation where he has exactly £ 5,00,000 payables after 3 months. This can be done by borrowing the present value of £ 5,00,000 as per the borrowing rates applicable in UK, which is 5% p.a.
Exposure and action to be taken Today:

Exposure and action to be taken Today
Asset	£ 5,00,000 receivables alter 3 months
Create	£ 5,00,000 liability after 3 months
Borrow	Present Value of £ 5,00,000 at 5% for 3 months = $\frac{£ 5,00,000}{1.0125}$ = £ 4,93,827.16
	Spot rate : ₹ 56.00/£ Conversion Value = £ 4,93,827.16 × ₹ 56 = ₹ 2,76,54,321
Invest	₹ 2,76,54,321(5) deposit rate in India i.e. 12% p.a.

Situation after 3 months

Receive	£ 5,00,000
Repay Loan with Int.	= £ 4,93,827.16 + £6172.84 = £ 5,00,000
Realise the Investment	= 2,76,54,321 × 1.03 = ₹ 2,84,83,950.64
Final Inflow in Rs.	₹ 2,84,83,950.64

Inflow at spot
5,00,000 × 56 = 2,80,00000
Therefore : Gain = 4,83,950.64 (2,84,8395064 – 2,80,00,000)
The gain will be even higher if £ depreciates

Question 43.
An Indian importer would like to cover itself against a likely increase of pound sterling. The following data is given:
Invoice: £ 1,00,000
Spot rate: ₹/£ 85.70/86.00
Payment date: 3 months

Country	3 months interest rate
Country	Deposit	Borrow
India	10%	12%
UK	5%	5.5%

Explain how a money market hedge can be used by the importer to protect himself from the rise in Pound. [Practice Question]
Answer:
Money Market Hedge:
Since the Indian importer has £ 1,00,000 payables after 3 months, he must create an opposite situation where he has exactly £ 1,00,000 receivables after 3 months. This can be done by lending the present value of £ 1,00,000 as per the deposit rates applicable in UK, which is 5% p.a.
Exposure and action to be taken Today

Liability	£ 1,00,000 payables after 3 months
Create	£ 1,00,000 Asset after 3 months
Deposit	Present Value of £ 1,00,000 at 5% for 3 months = $\frac{£ 100,000}{1.0125} $ = £98,765.43
Amount required to get £98765.43	Spot rate (ask): ₹ 86.00/£ Conversion Value = £98,765.43 × ₹ 86 = ₹ 84,93,827
Borrow	Rs. 84,93,827 @ borrowing rate in India i.e. 12% p.a.

Situation after 3 months

Receive	£ 1,00,000 from the deposit
Payment	Pay the exporter £ 1,00,000, received from the deposit.
Repay Loan with Int.	= 84,93,827 × 1.03 = ₹ 84,93,827 + 2,54,815 = ₹ 87,48,642
Final outflow in ₹	₹ 87,48,642 (irrespective of the exchange rate ₹ /£ prevailing at the time of making the payment.)

Question 44.
JKL Ltd., an Indian company has an export exposure of JPY1,00,00,000 payable August 31, 2014. Japanese Yen (JPY) is not directly quoted against Indian Rupee.
The current spot rates are:
INR/US $ = ₹ 62.22
JPY/US $ = JPY 102.34
It is estimated that Japanese Yen will depreciate to 124 level and Indian Rupee to depreciate against US $ to ₹ 65.
Forward rates for August 2014 are INR/US $ = ₹ 66.50
JPY/US $ = JPY 110.35
Required:
(i) Calculate the expected loss, if the hedging is not done. How the position will change, if the firm takes forward cover?
(ii) If the spot rates on August 31, 2014 are:
INR/US $ = ₹ 66.25
JPY/US $ = JPY 110.85
Is the decision to take forward cover justified? [May 2014] [5 + 3 = 8 Marks]
Answer:
Since the direct quote for ¥ and ₹ is not available it will be calculated by cross exchange rate as follows: ₹/$ × $/¥ = ₹/¥
Given: INR/US $ = 7 62.22
JPY/US $ = JPY 102.34
₹/ ¥ = 62.22/102.34 = 0.6080
Spot rate on date of export 1¥ = ₹ 0.6080
Similarly, Expected Rate of ¥ for August 2014 = ₹ 0.5242 (₹ 65/¥ 124)
&Forward Rate of ¥ for August 2014 = ₹ 0.6026 (₹ 66.50/¥ 110.35)

(i) Calculation of expected loss

If no hedging is done:
Value of export at the time of export (₹ 0.6080 × ¥ 10,000,000)	₹ 60,80,000
Estimated payment to be received on Aug. 2014 (₹ 0.5242 × ¥ 10,000,000)	₹ 52,42,000
Loss	₹ 8,38,000
If Forward Cover is taken:
7 Value of export at the time of export (7 0.6080 × ¥ 10,00,000)	₹ 60,80,000
7 Payment to be received under Forward Cover (7 0.6026 × ¥ 10,000,000)	₹ 60,26,000
Loss	₹ 54,000

There is loss despite taking the forward cover but by taking the forward cover, the loss is reduced to ₹ 54,000.

(ii) If Actual Rate of ¥ on August 2014 turns out to be = ₹ 0.5977 (₹ 66.25/¥ 110.85)

Value of export at the time of export (₹ 0.6080 × ¥ 10,000,000)

₹ 60,80,000

Estimated payment to be received on Aug. 2014 (₹ 0.5977 × ¥

10,000,000)

₹ 59,77,000

Loss

₹ 1,03,000

The decision to take forward cover is fully justified.

Question 45.
An Indian firm has exported goods worth ₹ 5,50,000. The exporter has invoiced the importer in JPY and raised an invoice of 10,00,000 Japanese Yen (JPY) based on current spot rate, payable after 3 months. The JPY is not directly quoted against Indian Rupee.
The current spot rates ₹:
INR/US $ = 7 65
JPY/US $ = JPY 118.18
It is estimated that Japanese Yen will depreciate to 135 level and Indian Rupee to depreciate against US $ to ₹ 68.
Forward rates after 3 months are
INR/US $ = ₹ 68.75
JPY/US $ = JPY 130
Required:
(i) Calculate the expected loss, if the hedging is not done. How the position will change, if the firm takes forward cover?
(ii) If the actual spot rates after 3 months are:
INR/US $ = ₹ 66.25
JPY/US $ = JPY 110.85
Is the decision to take forward cover justified? [Practice Question]
Answer:
Since the direct quote for ¥ and ₹ is not available it will be calculated by cross exchange rate as follows:
₹/¥ = ₹/$ × $/¥
Given: ₹/$ = ₹65
JPY/US $ = JPY 118.18
₹/¥ = 65/118.18 = 0.550
Spot rate on date of export 1¥ = ₹ 0.550
Similarly, Expected Rate of ¥ after 3 months = ₹ 0.5037 (₹68/¥ 135)
& Forward Rate of ¥ after 3 months = ₹ 0.5288 (₹68.75/¥ 130)
(i) Calculation of expected loss

If no hedging is done:
Value of export at the time of export (₹ 0.550 × ¥ 10,00,000)	₹ 5,50,000
Estimated payment to be received after 3 months (₹ 0.5037 × ¥ 10,00,000)	₹ 5,03,700
Loss	₹ 46,300
If Forward Coyer is taken:
Value of export at the time of export (₹ 0.550 × ¥ 10,00,000)	₹ 5,50,000
Payment to be received under Forward Cover (₹ 0.5288 × ¥ 10,000,000)	₹ 5,28,800
Loss	₹ 21,200

There is loss despite taking the forward cover but by taking the forward cover, the loss is reduced to ₹ 21,200 from the expected loss of ₹₹ 46,300.

(ii) If Actual Rate of ¥ on maturity turns out to be = ₹ 0.5977 (₹ 66.25/¥ 110.85)

Value of export at the time of export (₹ 0.550 × ¥ 10,00,000)	₹ 5,50,000
Estimated pavment to be received on maturity (₹ 0.5977 × ¥ 10,00,000)	₹ 5,97,700
Gain	₹ 47,700

The decision to take forward cover did not prove to be fruitful. JPY appreciated over a period of 3 months instead of expected fall in currency.

Question 46.
A company operating in a country having the dollar as its unit of currency has today invoiced sales to an Indian company, the payment being due three months from the date of invoice. The invoice amount is $ 13,750 and at today’s spot rate of $ 0.0275 per ₹ 1, is equivalent to ₹ 5,00,000.
It is anticipated that the exchange rate will decline by 5% over the three months period and in order to protect himself, the importer proposes to take appropriate action through foreign exchange market. The three months forward rate is quoted as $ 0.0273 per ₹ 1.
You are required to calculate the expected loss and to show, how it can be hedged by forward contract.
Answer:
Calculation of expected spot rate, if there is decline of 5°o over the three month in currency.
Decline in 3 months is 5%
Spot $/₹ = 0.0275
Decline by 5% = 0.0275(0.95) = 0.026125
Expected outflow = $13,750/0.026125 = ₹ 5,26,315.78.
Expected loss = ₹ 26,316 (5,00,000 – 5,26,316)
By taking forward cover the company can hedge itself and lock its payables at 13,750/0.0273, and total outflow of the importer would be 5,03,663. If the company would not have taken the forward contract it would have faced the risk of depreciation in the value of ₹ at expected spot rate it would have paid 5,26,316.
Therefore, the expected loss is reduced by ₹ 22,653 (5,26,316 – 5,03,663).

Question 47.
A company operating in Japan has today effected sales to an Indian company, the payment being due 3 months from the date of invoice. The invoice amount is 108 lakhs yen. At today’s spot rate, it is equivalent to ₹ 30 lakhs. It is anticipated that the exchange rate will decline by 10% over the 3 months period and in order to protect the yen payments, the importer proposes to take appropriate action in the foreign exchange market. The 3 months forward rate is presently quoted as 3.3 yen per rupee. You are required to calculate the expected loss and to show how it can be hedged by a forward contract. [Nov. 2003] [6 Marks]
Answer:
Spot rate of ₹ 1 against yen =108 lakhs yen/₹ 30 lakhs = 3.6 yen
3 months forward rate of Re. 1 against yen = 3.3 yen
Anticipated decline in Exchange rate = 10%
Expected spot rate after 3 months = 3.6 yen – 10°6 of 3.6 = 3.6 yen – 0.36 yen = 3.24 yen per rupee

	(₹ in lakhs)
Present cost of 108 lakhs yen	30
Cost after 3 months: 108 lakhs yen/3.24 yen	33.33
Expected exchange loss	3.33
If the expected exchange rate risk is hedged by a Forward contract:
Present cost	30
Cost after 3 months if forward contract is taken 108 lakhs yen /3.3 yen	32.73
Expected loss	2.73

Suggestion: If the exchange rate risk is not covered with forward contract, the expected exchange loss is ₹ 3.33 lakhs. This could be reduced to ₹ 2.73 lakhs if it is covered with Forward contract. Flence, taking forward contract is suggested.

Question 48.
A person gets an interest free loan of USD 1,50,000. Repayment is to be done in three equal half-yearly instalments.
Assume the following rates:

A. Today	Six months forward rate 42/42.50
B. At the end of six months Six months forward	spot 43/43.10 43.40/43.50
C. At the end of one year Six months forward	Spot 44/44.10 44.50/44.60
D. At the end of one & half year spot	45/45.10

Find the amount he has to pay in rupees in following three cases. Give your recommendation:
(i) No hedging
(ii) Rupee roll over forward
(iii) Three separate forward contracts, one today, one after six months and one after one year from today. (Ignore bank commission)
Answer:
(i) The amount he has to pay when there is no hedging
(a) At the end of 6 months – 50,000 × 43.10 = ₹ 21,55,000
(b) At the end of 1 year – 50,000 × 44.10 = ₹ 22,05,000
(c) At the end of 18 months – 50,000 × 45.10 = ₹ 22,55,000.
If no hedging is done payment will be based on the prevailing spot rate (ask) at the time of payment and total outflow is ₹ 66,15,000.

(ii) The amount he has to pay in case of Rupee rollover forward:

Working Notes (W.N)
(1) The borrower will enter into a forward contract to purchase $ 1,50,000 @ ₹ 42.50
After 6 months, execute the contract, use $50,000 to pay the first instalment and sell the balance $ 1,00,000 at the spot bid rate prevailing at the end of 6 months from today i.e. ₹ 43, simultaneously, enter with the bank to purchase $ 1,00,000 @ 6 months forward rate of 43.50.
Net effect [Pay (1,50,000 × 42.50) and receive (1,00,000 × 43)]
(63,75,000 – 43,00,000) = ₹ 20,75,000.

(2) After 1 year execute the contract, use $ 50,000 to pay the second instalment and sell the balance $ 50,000 at the spot bid rate prevailing at the end of 1 year from today i.e. ₹ 44, simultaneously, enter with the bank to purchase $ 50,000 @ 6 months forward rate of 44.60.
Net effect [Pay (1,00,000 × 43.50) and receive (50,000 × 44)]
(43,50,000 – 22,00,000) = ₹ 21,50,000.

(3) After 18 months execute the contract, use $ 50,000 to pay the last instalment @ ₹ 44.60.
Total outflow is ₹ 64,55,000

(iii) The amount he has to pay in case of Three forward contracts:

Total outflow is ₹ 65,30,000 To conclude:

Alternatives	Total Outflow (₹)
(i)	66,15,000
(ii)	64,55,000
(iii)	65,30,000

Hence, Rupee rollover forward contract is the best alternative as the outflow is least under the method.

Question 49.
On September 1,2017, ₹ /$ spot rate in New York is ₹ 51.90 and December £ futures are trading at $1.5950. The ₹ /£ spot rate on that day is ₹ 78.90. Neel Corporation has a 3 month sterling receivable of £1,00,000.
You are given that the standard size of sterling futures contracts is £ 62,500 and Neel Corporation decides to hedge its risk by trading in two sterling futures contracts. By December 1, 2017 the spot dollar has appreciated to ₹ 52.80, while the spot pound sterling has depreciated to ₹ 78.20. If December futures are trading at £ 1.5720, what is the profit or loss incurred by Neel Corporation? [Practice Question]
Answer:
Receipts using cross currency futures:

Particulars
1. Asset	Receivables £1,00,000
2. Time	3 months
3. Hedging through futures	Sell £ Futures
4. Standard size	£ 62,500 against $
5. No. of contracts	2 (Given in the question)
6. Future trading at	$1.5950
7. Future price at the time of settlement	$1.5720
8. Gain or loss on future	(1.5950 -1.5720) × 2 × 62,500 = $ 2,875 (Gain)
9. Total $ inflow + £ inflow	Receivables + Gain = $ 2,875 + £1,00,000
10. Total ₹ converted using spot after 3 months	US $ 2,875 × 52.80 = ₹ 1,51,800 £ 1,00,000 × 78.20 = ₹ 78,20,000
11. Net inflow	₹ 79,71,800 (1,51,800 + 78,20,00)

Question 50.
EFD Ltd. is an export business house. The company prepares invoice in customers’ currency. Its debtors of US$ 1,00,00,000 is due on April 1, 2015 is:

Exchange rates USS/INR		Currency Futures US$/INR
Spot 1- month forward 3 – months forward	0.016667 0.016529 0.016129	Contract size: 1 – month 3 – months	₹ 24,816,975 0.016519 0.016118

	Initial Margin	Interest rates in India
1-month	₹ 17,500	6.5%
3-months	₹ 22,500	7%

On April 1, 2015 the spot rate US$/INR is 0.016136 and currency future rates is 0.016134.
Which of the following methods would be most advantageous to EFD Ltd.?
(i) Using forward contract
(ii) Using currency futures
(iii) Not hedging the currency risk [May 2015] [6 Marks]
Answer:
(i) Receipts using forward contract:
This is indirect quotation for the Indian exporter who has $ 1,00,00,000 receivables, therefore the total receipts in Rs. will be: $ 1,00,00,000/0.016129
= Rs.62,00,01,240

(ii) Receipts using currency futures:

Particulars
1. Asset	Receivables $ 1,00,00,000 or $ 1,00,00,000/ 0.016118 = ₹ 62,04,24,370 (Using future price $/Rs. 0.016118 )
2. Time	3 months
3. Hedging through futures	Sell $ Futures or buy Rs. Futures. Here Rs. futures is available therefore buy Rs. futures
4. Standard size	₹ 2,48,16,975
5. No. of contracts	$ \frac{\mathrm{Rs} .62,04,24,370}{2,48,16,975} $ = 24.9999 = 25 Contracts
6. Future price	$/Rs. 0.016118
7. Initial margin	Rs. 22,500 per contract = Rs. 5,62,500 (22500 × 25) To be borrowed @ 7%
8. Future price at the time of settlement	0.016134
9. Gain or loss on future	(0.016134 – 0.016118) × 25 × 2,48,16.975 = $9926.79
10. Total $ inflow	Receivables + Gain = 1.00.00.000 – 9926.79 = 1,00,09,926.79
11. Total Rs. (converted using spot after 3 months)	US $ 1,00,09,926.79 0.016136 = Rs. 62,03,47,471
12. Interest cost	5,62,500 × 0.07 × 3/12 = Rs. 9844
13. Net inflow	Rs.62,03,37,627

(iii) Net receipts under when there is no hedging
US $ 1,00,00,000/0.016136 = ₹ 61,97,32,276

Method advantageous to EFD Ltd.
Since the receipts are highest when hedging is done through futures, therefore “Hedging through Futures” is the most advantageous method.

Question 51.
LMN Ltd. is an export oriented business house based in Mumbai. The Company invoices in customer’s currency. The receipt of US $ 6,00,000 is due on 1st September, 2016.
Market information as at 1st June, 2016 is:

On 1st September, 2016, the spot rate US $/₹ is 0.01461 and currency futures rate is US $/₹ 0.01462.
It may be assumed that variation in Margin would be settled on the maturity of the futures contract.
Which of the following methods would be most advantageous for LMN Ltd.:
(i) using Forward Contract,
(ii) using Currency Futures; and
(iii) not hedging Currency Risks
Show the calculations and comment. [Nov. 2016] [8 Marks]
Answer:
(i) Receipts using forward contract:
This is indirect quotation for the Indian exporter who has $ 6,00,000 receivables, therefore the total receipts in Rs. will be: $ 6,00,000/0.01458 = Rs. 4,11,52,263.37

(ii) Receipts using currency futures:

Particulars
Asset	Receivables $ 6,00,000 or $ 6,00,000/0.01449 = ₹ 4,14,07,867.50 (Using future price $/Rs.0.01449)
Time	3 months
Hedging through futures	Sell $ Futures or buy Rs. Futures. Here Rs. futures is available therefore buy Rs. futures
Standard size	₹ 30,00,000
No. of contracts	$\frac{\text { Rs. } 4,14,07,867.50}{30,00,000}$ = 13.8026 = 14 contracts
Future price	$/Rs. 0.01449
7. Initial margin	Rs. 16,000 per contract = Rs. 2,24,000 (16,000 × 14) To be borrowed @ 8.5%.
8.Future price at the time of settlement	0.01462
9. Gain on futures	(0.01462 – 0.01449) × 14 × 30,00,000 = $5,460
10. Total $ inflow	Receivables + Gain = 6,00,000 + 5,460 = 6,05,460
11. Total Rs. (converted using spot after 3 months) Less: Interest cost	US $ 6,05,460/0.01461 =Rs. 4,14,41,478 2,24,000 × 0.085 × 3 12= Rs. 4,760
12. Net inflow	Rs. 4,14,36718

(iii) Net receipts under when there is no hedging
US $ 6,00,000/0.01461 = ₹ 4,10,67,762
Method advantageous to LMNLtd.
Since the receipts are highest when hedging is done through futures, therefore “Hedging through Futures” is the most advantageous method.

Question 52.
JKL Ltd. is an export business house. The company prepares invoice in customers’ currency.
Its debtors of US$.2,00,00,000 is due on April 1, 2017.
Market information as at January 1, 2017 is:

On April 1, 2017 the spot rate US$/INR is 0.016136 and currency future rate is 0.016134.
Which of the following methods would be most advantageous to JKL Ltd.?
(i) Using forward contract
(ii) Using currency futures
(iii) Not hedging the currency risk [Nov. 2017] [8 Marks]
Answer:
(i) Receipts using forward contract:
This is indirect quotation for the Indian exporter who has $ 2,00,00,000 re’ ceivables, therefore the total receipts in Rs. will be: $ 2,00,00,000/0.016129 = Rs. 1,24,00,02,480

(ii) Receipts using currency futures:

Particulars
1. Asset	Receivables $ 2,00,00,000 or S 2,00,00,000/ 0.016118 = ₹ 1,24,08,48,740 (Using future price $/Rs. 0.016118)
2. Time	3 months
3. Hedging through futures	Sell $ Futures or buy Rs. Futures. Here Rs. futures is available therefore buy Rs. Futures
4. Standard size	₹ 31,021,218
5. No.of contracts	$\frac{\mathrm{Rs} .1,24,08,48,740}{31,021,218}$ = 40 Contracts
6. Future price	$/Rs. 0.016118
7. Initial margin	Rs. 50,000 per contract = Rs. 20,00,000 (50,000 × 40) To be borrowed @ 8.0%
8. Future price at the time of settlement	0.016134
9. Gain on futures	(0.016134 – 0.016118) × 40 × 31,021,218 = $19,853.58
10. Total $ inflow	Receivables + Gain = 2,00,00,000 + 19,853.58 = 2,00,19,853.58
11.Total Rs. (converted using spot after 3 months) Less: Interest cost	US $ 2,00,19853.58/0.016136 = Rs. 1,24,06,94,941 20,00,000 × 0.08 × 3 12 = Rs. 40,000
12. Net inflow	Rs. 1,24,06,54,941

(iii) Net receipts under when there is no hedging
US $ 2,00,00,000/0.016136 = ₹ 1,23,94,64,551
Method advantageous to JKL Ltd.
Since the receipts are highest when hedging is done through futures, therefore “Hedging through Futures” is the most advantageous method.

Question 53.
Sunshine Ltd. is an export business house. The company prepares invoice in customers’ currency. Its debtors of US$ 2,00,000 is due on April 1, 2018.
Market information as at January 1, 2018 is:

Exchange rates US$/INR

Currency Futures US$/INR

Spot

1 – month forward
3 – months forward

0.014717

0.014719

0.014815

Contract size:
1 – month
3 – months

₹ 26,99,975
0.014812
0.014830

	Initial Margin	Interest rates in India
1-month 3-months	₹ 1,850 ₹ 2,750	8.5% 9%

On April 1, 2018 the spot rate US$/INR is 0.014840 and currency future rates is 0.014842.
Which of the following methods would be most advantageous to Sunshine Ltd.?
(i) Using forward contract
(ii) Using currency futures
(iii) Not hedging the currency risk
Answer:
(i) Receipts using forward contract:
This is indirect quotation for the Indian exporter who has ₹ 2,00,000 receivables, therefore the total receipts in ₹ will be : $ 2,00,000/0.014815 = ₹ 1,34,99,831

(ii) Receipts using currency futures:

Particulars
1. Asset	Receivables $ 2,00,000 or $ 2,00,000/0.014830 = ₹ 1,34,86,177(Using future price $/₹ 0.014830)
2. Time	3 months
3. Hedging through futures	Sell $ Futures or buy ₹ Futures. Here ₹ futures is available therefore buy ₹ futures for 3 months
4. Standard size	₹ 26,99,975
5. No. of contracts	$ \frac{\text { Rs. } 1,34,86,177}{26,99,975} $ = 4.9949 = 5 Contracts
6. Future price at the time of contract	0.014830
7. Initial margin	₹ 2,750 per contract = ₹ 13,750 (2,750×5) To be borrowed @ 9%.
8. Future price at the time of settlement	$/₹ 0.014842
9. Gain or loss on future	(0.014842 – 0.014830) × 5 × 26,99,975 = $161.9985
10. Total $ inflow	Receivables + Gain = 2,00,000 + 161.9985 = 2,00,161.9985
11. Total ₹ converted using spot after 3 months	US $ 2,00,161.9985/0.014840 = ₹ 1,34,88,005
12. Interest cost	13,750 × 0.09 × 3/12 = ₹ 309.375= 309 (Rounded off)
13. Net inflow	₹ (1,34,88,005 – 309) = 1,34,87,696

(iii) Net receipts, when there is no hedging
US $ 2,00,000/0.014840 = ₹ 1,34,77,089
To sum up:

option	Particulars	₹
(i)	Use of Forward contract	1,34,99,831
(ii)	Use of Future contract	1,34,87,696
(iii)	No hedging	1,34,77,089

Method advantageous to Sunshine Ltd.
Since the receipts are highest when hedging is done through Forward contract, therefore ‘‘Hedging through Forward” is the most advantageous method.

Question 54.
Saagar Ltd. is an importer who has imported goods worth £5,00,000. The U.K Company enjoys substantial goodwill and its products are in much demand, therefore, it always prepares invoice for all the clients in its home currency only. Its payment, £5,00,000 is due on 30th June, 2018.
Market information as at April 1, 2018 is:

Exchange rates US$/INR		Currency Futures US$/INR
Spot 3 – months forward	0.011176 0.011150	Contract size: 3 – months	₹ 17,90,190 0.011172

	Initial Margin	Interest rates in India
3-months	₹ 7,500	9%

On June 30, 2018 the spot rate £/₹ is 0.011180 and currency future rates is 0.011182.
Which of the following methods would be most advantageous to Saagar Ltd.?
(i) Using forward contract
(ii) Using currency futures
(iii) Not hedging the currency risk
Answer:
(i) Outflow in Rupees using forward contract:
This is indirect quotation for the Indian importer who has to pay £ 5,00,000 therefore, the total payment in ₹ will be £ 5,00,000/0.011150 =
₹ 4,48,43,049

(ii) Outflow using currency futures:

Particulars
1. Liability	Payment of £ 5,00,000 or £5,00,000/0.011172 = ₹ 4,47,54,744 (Using future price $/₹ 0.011172)
2. Time	3 months
3. Hedging through futures	Buy £ Futures or Sell ₹ Futures. Here ₹ futures is available therefore Sell ₹ futures for 3 months
4. Standard size	₹ 17,90,190
5. No. of contracts	$\frac{\text { Rs. } 4,47,54,744}{17,90,190}$ = 24.9999 = 25 Contracts
6. Future price at the time of contract	0.011172
7. Initial margin	₹ 7,500 per contract = ₹ 1,87,500 (7,500 × 25) to be borrowed @ 9%.
8. Future price at the time of 9set9tlement	S/₹ 0.011182
9. Gain or loss on future	(0.011172 – 0.011182) × 25 × 17,90,190 = £ 447.5475 It is loss
10. Total £ to be paid	Payables + Loss = 5,00,000 + 447.5475 = 5,00,447.5475
11. Total ₹ converted using spot after 3 months	£5,00,447.5475/0.011180 = ₹ 4,47,62,750
12. Interest cost	1,87,500 × 0.09 × 3/12 = ₹ 4218.75 = 4219 (Rounded off)
13. Net outflow	₹ 4,47,66,969 (4,47,62,750 + 4,219)

(iii) Net outflow when there is no hedging
£ 5,00,000/0.011180 = ₹ 4,47,22,719
To sum up:

Option	Particulars	₹
(i)	Use of Forward contract	4,48,43,049
(ii)	Use of Future contract	4,47,66,969
(iii)	No hedging	4,47,22,719

Method which is most advantageous to Saagar Ltd.:
Since the outflow is least when hedging is not done, therefore “No Hedging” is the most advantageous method. No hedging has been more advantageous as the £ has depreciated rather than appreciating, as per the expectation. However, risk will prevail if no hedging is done.

Question 55.
On 19th April following are the spot rates Spot EURO/USD 1.20000 USD/INR 44.8000 Following are the quotes of European options:

(i) A trader sells an at-the-money spot straddle expiring at three months (July 19).
Calculate gain or loss if three months later the spot rate is EURO/USD 1.2900.
(ii) Which strategy gives a profit to the dealer if five months later (Sep. 19) expected spot rate is USD/INR Rs. 45.00. Also calculate profit for a transaction USD 1.5 million. [May 2009] [8 Marks]
Answer:
(i) A trader sells Straddle of “At the Money” 3 months i.e. July 19, so he will be selling a call option & a put option with a strike Price of USD 1.20000 per EURO as the spot is also same. “Spot EURO/USD =1.20000 (Straddle is a option strategy of a CALL & a PUT option with identical Strike Price and identical maturity.)
Premium received = $ 0.035 (Call)+ $0,040 (Put) = $ 0.075
After three months, Spot rate is 1.290. This is more than the strike price therefore call option is exercisable but the put option will lapse. The buyer of the Call option will exercise the option, but buyer of Put option will allow the option to lapse.
Profit or Loss to a trader is

Premium received	S 0.075
Loss on call option exercised (1.2900 – 1.200)	$ 0.090
Net Loss per €	$0,015

(ii) If five months later expected USD/INR = 45 and a buy strategy is adopted then call option should be bought. It will be beneficial as the price is expected to go up.
Premium payable for buying call option on 19th – ₹ 0.12 April.
gain on exercise of call option on 19th September ₹ 0.20 – (₹ 45 – 44.80)
Net Gain or Profit – ₹ 0.08
Total profit on a transaction of USD 1.5 million (15,00,000 × 0.08) = ₹ 1,20,000
Alternatively the trader may also sell the put option and earn a premium of Rs.0.04 per $. Total profit will be $ 15,00,000 × 0.04 = Rs. 60,000.

Question 56.
An American firm is under obligation to pay interests of Can$ 10,10,000 and Can$ 7,05,000 on 31st July and 30th September respectively. The Firm is risk averse and its policy is to hedge the risks involved in all foreign currency transactions. The Finance Manager of the firm is thinking of hedging the risk considering two methods i.e. fixed forward or option contracts.
It is now June 30, following quotations regarding rates of exchange, US$ per Can$, from the firm’s bank were obtained :

Spot	1 Month Forward	3 Months Forward
09284 – 0.9288	0.9301	0.9356

Price for a Can$/US$ option on a U.S. stock exchange (cents per Can$, payable on purchase of the option, contract size Can$ 50000) are as follows:

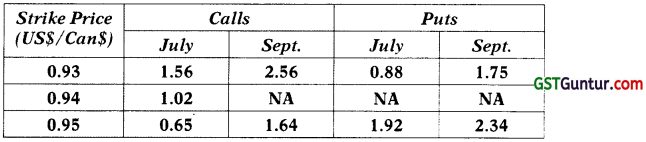
According to the suggestion of finance manger if options are to be used, one month option should be bought at a strike price of 94 cents and three month option at a strike price of 95 cents and for the remainder uncovered by the options the firm would bear the risk itself. For this, it would use forward rate as the best estimate of spot. Transaction costs are ignored.
Recommend, which of the above two methods would be appropriate for the American firm to hedge its foreign exchange risk on the two interest payments. [Nov, 2013]
Answer:
Method-1 (Hedging using Forward Cover)

Particulars	July	September
Amount to be paid in Can $ (A)	10,10,000	7,05,000
Forward rate applicable for Can $ (B)	0.9301	0.9356
Total Outflow in US$ (A) × (B)	9,39,401	6,59,598

Method-2 (Hedging using Options)
Option Contracts standard Size = Can$ 50,000
Number of contracts required:
For July = 10,10,000/50,000 = 20.20 rounded off to 20
For September = 7,05,000/50,000 = 14.10 rounded off to 14
The finance manager has chosen a Strike Price of 0.94 US $ for July option at a premium of 1.02 cents and a Strike Price of 0.95 US $ for September option at a premium of 1.64 cents
Company would like to take out 20 contracts for July (covering Can $ 10,00,000) and 14 contracts for September (covering Can $ 7,00,000) respectively. The call options on Can $ would be bought as the need is to buy Can $. Therefore costs, if the options were exercised, (assuming actual rates are higher) will be:

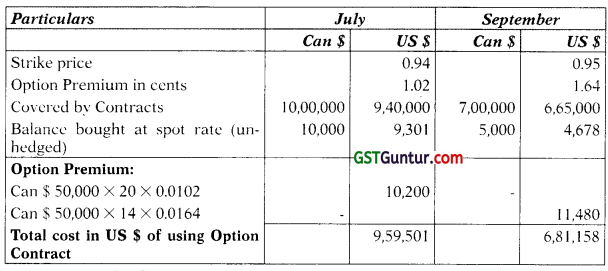
Decision: As the firm is stated as risk averse and the money due to be paid is certain, a fixed forward contract, being the cheapest alternative in the both the cases, would be recommended.

Question 57.
XYZ, an Indian firm, will need to pay JAPANESE YEN (JY) 5,00,000 on 30th June. In order to hedge the risk involved in foreign currency transaction, the firm is considering two alternative methods i.e. forward market cover and currency option contract.
On 1st April, following quotations (JY/INR) are made available:
Spot – 3 months forward
1.9516/1.9711 – 1.9726/1.9923
The prices for forex currency option on purchase are as follows:
Strike Price – JY 2.125
Call option (June) – JY 0.047
Put option (June) – JY 0.098
For excess or balance of JY covered, the firm would use forward rate as future spot rate.
You are required to recommend cheaper hedging alternative for XYZ. [Nov. 2015] [5 Marks]
Answer:
Indian importer requires to pay Japanese Yen, therefore it needs to buy Japanese Yen and ask rate will be applicable. Since this is inverse quote, therefore, ask rate will be 1/bid.
(i) Forward Cover:
3 month Forward Rate = $\frac{1}{1.9726}$ = Rs. 0.5070/JY
Accordingly INR required for JY 5,00,000 (5,00,000 × ₹ 0.5070) ₹ 2,53,500

(ii) Option Cover:
As the Indian importer requires to pay Japanese Yen, therefore it needs to buy Japanese Yen so if call option is available on JPY it can buy it but the option is on INR and XYZ need to purchase JY 5,00,000, therefore it needs to sell INR, so, XYZ shall enter into a Put Option @ JY 2.125/INR
Accordingly, outflow in INR$\left(\frac{\mathrm{JY} 5,00,000}{2.125}\right)$ = ₹ 2,35,294
Premium$\left(\frac{\text { INR } 2,35,294 \times 0.098}{1.9516}\right)$ = ₹ 11,815

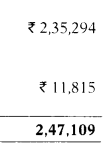
Since, outflow of cash is less in case of Option same should be opted for. Further, if price of INR goes above JY 2.125 /INR the outflow will further be reduced. Interest on premium is ignored.

Question 58.
ABC Ltd., a US Firm, will need £ 5,00,000 in 180 days. In this connection, the following information is available:
Spot Rate 1 £ = $ 2.00
180 days forward rate of £ as of today is $ 1.96

Interest rates are as follows:	US	UK
180 days deposit rate	5.0%	4.5%
180 days borrowing rate	5.5%	5.0%

A call option on £ that expires in 180 days has an exercise price of $ 1.97 and a premium of $ 0.04.
ABC Ltd. has forecasted the spot rates for 180 days as below:
Future rate Probability

$ 1.91	30%
$ 1.95	50%
$ 2.05	20%

Which of the following strategies would be cheaper to ABC Ltd.?
(i) Forward Contract;
(ii) A money market hedge;
(iiii) A call option contract; and
(iv) No hedging option [Nov. 2015] [8 Marks]
Answer:
(i) Forward Contract Hedge:
Amount Payable =£ 5,00,000
180 days forward rate of £ as of today is
outflow in $ [5,00,000 × $ 1.96] = $ 9,80,000

(ii) Money Market Hedge :
Since the US Firm needs £ 5,00,000 after 180 days, it must create an opposite situation where it has exactly £5,00,000 receivable after 180 days. This can be done by depositing or lending the present value of £ 5,00,000 as per the lending rates applicable in UK, which is 4.5% (Assumed to be p.a.)

Exposure and action to be taken Today
Liability	£ 5,00,000 needed after 180 days
Create	£ 5,00,000 asset after 180 days
Lend	Present Value of £ 5.00,000 at 4.5% for 180 days = $\frac{£ 5,00,000}{1.0225}$ = £ 4,88,997.33
Convert$ into £	Spot Rate 1 £ = 8 2.00 Conversion Value = £ 4,88,997.55 X 2 = $9,77,995.10
Borrow	$9,77,995.10 (a Borrowing rate in US i.e. 5.5 % p.a.
Situation after 180 days
Repay Loan with Int.	= $9,77,995.10+ S 26895 = $ 10,04,890.10
Final outflow in $	$ 10,04,890.10

(iii) Call option on £ at an exercise price of $ 1.97 and a premium of $ 0.04. The call option will be exercised only when the spot rate exceeds the strike price (i.e. $ 1.97)

(iv) No Hedging

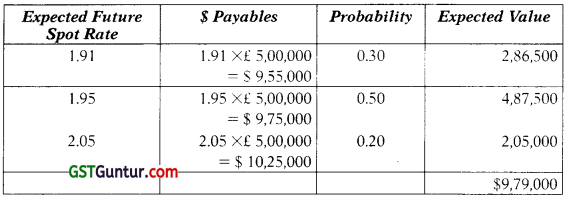
Since the expected outflow is least when no hedging is done, therefore hedging is not advisable.

Question 59.
Unilever’s subsidiary in India, Hindustan Lever, procures most of its soaps from a Japanese company. Because of the shortage of working capital in India, payments terms for the Indian importers are typically 180 days or more. Hindustan Lever wishes to hedge a 8.5 million Japanese Yen payable. Although options are not available on the Indian Rupee (₹), forward rates are available against the Yen. Additionally, a common practice in India is, for companies like Hindustan Lever, to work with a currency agent who will, in this case, lock in the current spot exchange for a 4.85% fee. Using the following data, recommend a hedging strategy.

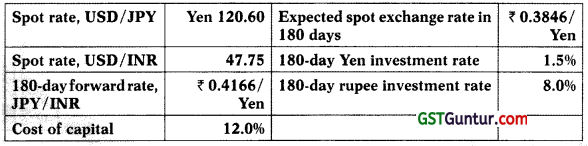
Answer:
Amount payable in 180 days = ¥85,00,000
Spot (₹/¥) = $\frac{1}{¥ / \$}$ × (₹/$)
$\left(\frac{1}{120.60}\right)$ × (47.75)
= 0.3959

Rate	(₹/¥) Direct Quote	(¥/₹) Indirect Quote
Spot	0.3959	2.5257
Forward	0.4166	2.4004
Expected spot	0.3846	2.6001

Option 1: Use of Forward contract: ₹ 35,41,100 (85,00,000 × 0.4166).
Option 2: Currency agent’s proposal: To lock the current price and pay 4.85% as fees on the amount
= ₹ 33,65,150 (85,00,000 × 0.3959) + 4.85%
= ₹ 35,28,360
Note: It may be assumed that the interest charges on fees paid is ignored.
Option 3: Money market hedge:

Exposure and action to be taken Today
Liability	¥ 8.5 million payable after 180 days
Create	¥ 8.5 million asset after 180 days
Lend	Present Value of ¥ 8.5 million at 1.5% = $\frac{¥ 8.5{1.0075} $ ⁼ ¥ 8.436724 million
Convert ₹ into 8.436724 million ¥ at spot rate	Conversion Value = (0.3959 × 84,36,724) = 33,40,100
Borrow	₹ 33,40,100 @ 12.0% in India.
Situation after 3 months
Receive	¥ 8.5 million
Pay to the exporter	¥ 8.5 million
Repay the loan at 6% for 180 days	33,40,100 (1.06) = 35,40,506.
Final outflow in ₹	₹ 35,40,506

Option 4: Remain un-hedged. Expected outflow = ₹ 32,69,100 (85,00,000 × 0.3846)
To sum up:

Option	Particulars	₹
(i)	Use of Forward contract	35,41,100
(ii)	Agents proposal	35,28,360
(iii)	Use of Money Market Fledge	35,40,506
(iv)	No hedging	32,69,100

Option 4 has the least outflow but at the same time it is risky so if hedging is to be recommended, agent’s proposal is the best hedging strategy.

Question 60.
Roger Ltd., a UK company has received an order amounting to € 2 million from a German. The terms of contract includes 6 months credit period. The following three alternatives are being considered for managing the transaction risk by the UK based company. The German buyer is aware of the volatility in exchange rates but is open to invoicing in £ or in € as he is uncertain of the direction.
(i) Invoice the German firm in Sterling using the current exchange rate to calculate the invoice amount.
(ii) Alternatively invoicing the German firm in € and using a forward foreign exchange contract to hedge the transaction risk.
(iii) Invoice the German in € and use sufficient 6 months sterling future contracts (to the nearly whole number) to hedge the transaction risk.
Following data is available:

Spot Rate	€1.1750 €1.1770/£
6 months forward premium	0.50 0.55 Euro Cents
6 months future contract is currently trading at	€1.1760/£
6 months future contract size is	£62500
Spot rate (after 6 months)	€1.1792/£
6 months future rate	€1.1785/£

Required:
(a) Calculate to the nearest £, the receipt for Roger Ltd., under each of the three proposals.
(b) In your opinion, which alternative would you consider to be the most appropriate and the reason thereof.
Answer:
(a) Calculation of receipts in £ under each of the three proposals:
(i) Invoicing in £(Home Currency) instead of invoicing in (foreign currency):
When the invoice is raised in home currency, there is no need for any hedging.
Spot Rate = €1.1750 -1.1770/£
Invoicing in £ will produce
= $\frac{€ 2 \text { million }}{1.1770}$ = £ 16,99,235 (Rounded off to whole no.)

(ii) Use of Forward Contract:
Forward Rate = Spot Rate + forward premium (Ask rate) 1.1770 + 0.0055 = 1.1825
Using Forward Market hedge Sterling receipt would be $\frac{€ 2 \text { million }}{1.1825}$ = £ 16,91,332

(iii) Use of Future Contract
Since, the UK company is exporter it will buy £ futures. The equivalent sterling of the order placed based on future price
(€ 1.1760) = $\frac{€ 2.00 \text { million }}{1.1760}$ = £ 17,00,680
Number of Contracts = $\frac{£ 17,00,680}{62.500}$ = 27.21 Contracts
= 27 contracts (Rounded off to the nearest whole number)
Thus, amount hedged by future contract will be
= 27 × £ 62,500 = £ 16,87,500
Buy Future at – €1.1760
Sell Future at – €1.1785
Gain – € 0.0025
Total profit on Future Contracts = 27 × £ 62,500 × € 0.0025 = €4219

Amount Received	€2000000
Add: Profit on Future Contracts	€4219
	€2004219

Thus, the receipts under the three alternatives are:

Option	Particulars	£
(i)	Invoicing in £	£ 16,99,235
(ii)	Use of Forward contract	£ 16,91,332
(iii)	Use of Future contract	£16,99,643

(b) Based on the calculations in part (a) of the solution, alternative (iii) is most preferable because the receipts are highest under the alternative. Therefore hedging should be done using futures.

Question 61.
Nitrogen Ltd, a UK company is in the process of negotiating an order amounting to €4 million with a large German retailer on 6 months credit. If successful, this will be the first time that Nitrogen Ltd. has exported goods into the highly competitive German market. The following three alternatives are being considered for managing the transaction risk before the order is finalized.
(i) Invoice the German firm in Sterling using the current exchange rate to calculate the invoice amount.
(ii) Alternative of invoicing the German firm in € and using a forward foreign exchange contract to hedge the transaction risk.
(iii) Invoice the German firm in € and use sufficient 6 months sterling future contracts (to the nearly whole number) to hedge the transaction risk.
Following data is available :

Spot Rate	€1.1750 – €1.1770/£
6 months forward premium	0.60 – 0.55 Euro Cents
6 months future contract is currently trading at	€1.1760/£
6 months future contract size is	£62500
Spot rate and 6 months future rate	€1.1785/£

Required:
(а) Calculate to the nearest £, the receipt for Nitrogen Ltd., under each of the three proposals. [Nov. 2011] [4 Marks]
(b) In your opinion, which alternative would you consider to be the most appropriate and the reason therefore. [4 Marks]
Answer:
(a) Calculation of receipts in £ under each of the three proposals:
(i) Invoicing in £ (Home Currency) instead of invoicing in (foreign currency):
When the invoice is raised in home currency, there is no need for any hedging.
Spot Rate = €1.1750 -1.1770/£
Invoicing in £ will produce
= $\frac{€ 4 \text { million }}{1.1770}$ = £ 33,98,471 (Ask rate will be used)

(ii) Use of Forward Contract:
In this question forward premium points are given, which are decreasing i.e. the premium is less in ask than the bid, which is generally not the case, because generally premium is mentioned in ascending order and discount is mentioned in descending order. However, as the question is specifically using the word premium, we may consider it as premium.
Forward Rate = Spot rate + forward premium (Ask rate)
1.1770 + 0.0055 = 1.1825
Using Forward Market hedge Sterling receipt would be
$\frac{€ 4 \text { million }}{1.1825}$ = £ 33 82 664

(iii) Use of Future Contract
The equivalent sterling of the order placed based on future price
(€1.1760) = $\frac{€ 4.00 \text { million }}{1.1760}$ = £ 34,01,360.54
Number of Contracts = $\frac{£ 3401360.54}{62,500}$ = 54.4217 Contracts
= 54 contracts (Rounded off to the nearest whole number)
Thus, amount hedged by future contract will be = 54 × £ 62,500 = £ 3375000
Buy Future at = €1.1760
Sell Future at = €1.1785
= €0.0025

Total profit on Future Contracts = 54 × £ 62,500 × € 0.0025 = €8438
Amount Received = €4000000
Add: Profit on Future Contracts = €8438
= €4008438
Receipts
On sale of receipts at spot = $\frac{€ 4008438}{1.1785}$ = £34,01,305
(b) Proposal (iii) is most preferable because the receipts are highest under this.
However, if the forward points are considered as discount rates then the option (ii) will produce highest receipts in £(Pound) and it will become most preferable. This calculation is shown below:

Forward Contract:
Forward Rate = 1.1770 – 0.0055 = 1.1715
Using Forward Market hedge Sterling receipt would be $\frac{€ 4 \text { million }}{1.1715}$ = £ 34,14,426

Question 62.
DSE Ltd. is an export oriented business in Kolkata. DSE Ltd. invoices in customers’ currency.
Its receipts of US$.3,00,000 is due on July I, 2019.
Market information as at April 1, 2019:

Exchange rates US$/₹		Currency Futures US$/₹
Spot	0.0154	Contract Size: ₹ 6,40,000
1 month forward	0.0150	April	0.0155
3 months forward	0.0147	July	0.0151

	Initial Margin	Interest rates in India
April	₹ 13,000	9%
July	₹ 24,000	8.5%

On July, the spot rate US$/₹ is 0.0146 and currency future rate is 0.0147.
Comment which of the following methods would be most advantageous to DSE Ltd.?
(i) Using forward contract
(ii) Using currency futures
(iii) Not hedging the currency risk
It may be assumed that variation in margin would be settled on the maturity of the futures contract. [May 2019 old syllabus][8 Marks]
Answer:
(i) Receipts using forward contract:
This is indirect quotation for the Indian exporter who has $ 3,00,000 receivables, therefore the total receipts in ₹ will be: $ 3,00,000/0.0147 = ₹ 2,0408,163.27

(ii) Receipts using currency futures:

Particulars
1. Asset	Receivables $ 3,00,000 or 3,00,000/0.0151 = ₹ 1,98,67,549.66 (Using future price $/₹ 0.0151)
2. Time	3 months
3. Hedging through futures	Sell $ Futures or buy ₹ Futures. Here ₹ futures is available therefore buy ₹ futures
4. Standard size	₹ 6,40,000
5. No. of contracts	$ \frac{\text { Rs. } 1,98,67,550}{6,40,000}$ = 31.04 Contracts = 31 contracts
6.Future price on the date of contract	$/₹ 0.0151
7. Initial margin	₹ 24000 per contract = ₹ 7,44,000 (24,000 × 31) to be borrowed @ 8.5%
8. Future price at the time of settlement	0.0147
9. Loss on futures	(0.0151-0.0147) × 31 × 6,40,000 = $7936
10. Total $ inflow	Receivables – Loss = 3,00,000 – 7936 = 2,92,064
11. Total ₹ converted using spot after 3 months	US $ 2,92,064/0.0146 = ₹ 2,00,04,384
12. Interest cost	7,44,000 × 0.085 × 3/12 = ₹ 15,810
13. Net inflow	₹ (2,00,04,384 – 15,810) = 19988574

Tutorial Note: The given answer is different from the suggested answer of ICAI, in which the loss on future of $7,936 equivalent to Rs. 5,43,562 has been wrongly added as if it is again.

(iii) Net receipts under when there is no hedging
US $ 3,00,000/0.0146 = 2,05,47,945.20
Thus, the receipts (rounded off) under the three alternatives are:

Option	Particulars	₹
(i)	Use of Forward contract	2,04,08,163
(ii)	Use of Future contract	1,99,88,574
(iii)	No hedging	2,05,47,945

Method advantageous to DSELtd.
Since the receipts are highest when no hedging is done, therefore “No Hedging is recommended” it is the most advantageous method however there is some risk under this method.

Question 63.
Sun Ltd., an Indian company, will need $ 5,00,000 in 90 days. In this connection, the following information is given below:
Spot Rate 1 $ = ₹ 71
90 days forward rate of $1 as of today is = ₹ 73
Interest rates are as follows:

Particulars	US	India
90 days Deposit rate	2.50%	4.00%
90 days Borrowing rate	4.00%	6.00%

A call option on $ that expires in 90 days has an exercise price of ₹ 74 and a premium of ₹ 0.10.
Sun Ltd. has forecasted the spot rates for 90 days as below:

Future rate	Probability
₹ 72.50	25%
₹ 73.00	50%
₹ 74.50	25%

Which of the following strategies would be the most preferable to Sun Ltd.?
(i) A Forward Contract;
(ii) A money market hedge;
(iii) An option contract;
(iv) No hedging. [May 2019] [8 Marks]
Answer:
(i) Forward Contract Hedge:
Amount Payable = $ 5,00,000
90′ days forward rate of $ = ₹ 73
Total outflow in ₹ [$5,00,000 × 73] = ₹ 3,65,00,000

(ii) Money Market Hedge:
Since the Indian Company needs $ 5,00,000 after 90 days, it must create an opposite situation where it has exactly $ 5,00,000 receivable after 90 days. This can be done by depositing or lending the present value of $ 5,00,000 as per the lending rates applicable in US, which is 2.50% p.a. It has been assumed that the interest rates are given on p.a. basis.

Exposure and action to be taken Today
Liability	$ 5,00,000 payables after 90 days
Create	$ 5,00,000 receivables after 90 days
Therefore, Lend	Present Value of $ 5,00,000 at 2.5% p.a. for 90 days = $\frac{\$ 5,00,000}{1.00625}$ = $ 4,96,894.41
Convert ₹ into $ 4,99,750.125	Spot Rate 1$ = ₹ 71 Conversion Value = $ 4,96,894.41 × 71 = ₹ 3,52,79,503.11 = 3,52,79,503 approx.
Borrow	₹ 3,52,79,503 @ Borrowing rate in India i.e. 6 % p.a.
Situation after 90 days
Repay Loan with Int.	= ₹ 3,52,79,503 + ₹ 5,29,192.55 = ₹ 3,58,08,695.55
Receive and pay	$ 5,00,000
Final outflow in ₹	₹ 3,58,08,695.55

(iii) Call option on $ at an exercise price of ₹ 74 and a premium of ₹ 0.10. The call option will be exercised onlv when the spot rate exceeds the strike price (i.e. ₹ 74)

Note: Interest on premium is ignored. If interest on premium is considered, then it will be Rs. 3,000 (Calculated as 50,000@6%). In that scenario, the total outflow will be the sum of Rs. 3,66,12,500 and Rs. 3,000 i.e. Rs. 3,66,15,500.

(iv) No Hedging

Expected Future Spot Rate	Probability	Expected Value
₹ 72.50	0.25	18.125
₹ 73.00	0.50	36.500
₹ 74.50	0.25	18.625
		73.25
Total Outflow in ₹ = (5,00,000 × 73.25) = 3,66,25,000

Thus, the outflow, under the various alternatives, is:

Option	Particulars	₹
(i)	Use of Forward contract	3,65,00,000
(ii)	Money Market hedge	3,58,08,695
(iii)	Option contract	3,66,12,500
(iv)	No hedging	3,66,25,000

Since the expected outflow is least when hedging is done through money- market, therefore, money-market hedge should be used for hedging $ 5,00,000.

Question 64.
ABC Ltd., a US Firm, will need £ 1,00,000 in 3 months. In this connection, the following information is available:
Spot Rate 1 £ = $ 1.35
3 months forward rate of £ as of today is $ 1.40

Interest rates are as follows:	US	UK
3 months deposit rate	5.0%	4.5%
3 months borrowing rate	5.5%	5.0%

A call option on £ that expires in 180 days has an exercise price of $ 1.38 and a premium of $ 0.04.
ABC Ltd. has forecasted the spot rates for 3 months as below:

Future rate	Probability
$ 1.32	30%
$ 1.35	50%
$ 1.60	20%

Which of the following strategies would be cheaper to ABC Ltd.?
(i) Forward Contract;
(ii) A money market hedge;
(iii) A call option contract; and
(iv) No hedging option
Answer:
(i) Forward Contract Hedge:
Amount Payable = £ 1,00,000
3 months forward rate of £ as of today is outflow in $ [1,00,000 × $ 1.40] = $ 1,40,000

(ii) Money Market Hedge:
Since the US Firm needs £ 1,00,000 after 3 months, it must create an opposite situation where it has exactly £1,00,000 receivable after 3 months. This can be done by depositing or lending the present value of £ 1,00,000 as per the lending rates applicable in UK, which is 4.5% p.a.

Exposure and action to be taken Today
Liability	£ 1,00,000 needed after 3 months
Create	£ 1,00,000 asset after 3 months
Lend	Present Value of £ 1,00,000 at 4.5% for 3 months = $\frac{1,00,000}{1.01125}$ = 98,887.50£
$ needed to get £ 98,887.50	Spot Rate 1 £ = S 1.35 Conversion Value = £ 98,887.50 × 1.35= $133498.14
Borrow	$1,33,498.14 (a Borrowing rate in US i.e. 5.5% p.a.
Situation after 3 months
Repay Loan with Int.	= $1,33,498.14 (1.01375) = $ 1,35,334 (approx.)
Realise the amount lent in £	£1,00,000
Make the payment due in £	£1,00,000
Final outflow in $	$ 1,35,334

(iii) Call option on £ at an exercise price of $ 1.38 and a premium of $ 0.04. The call option will be exercised only when the spot rate exceeds the strike price (i.e. $ 1.38)

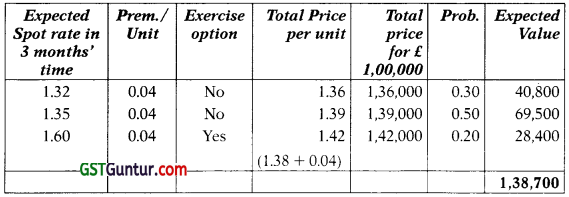
Note: The interest cost on premium paid is ignored.

(iv) No Hedging

Expected Future Spot Rate	$ Payables	Probability	Expected Value
1.32	1.32 × £ 1,00,000 = $ 1,32,000	0.30	39,600
1.35	1.35 × £ 1,00,000 = $ 1,35,000	0.50	67,500
1.60	1.60 × £ 1,00,000 = $ 1,60,000	0.20	32,000
			1,39,100

Option	Particulars	$
(i)	Use of Forward contract	1,40,000
(ii)	Use of Money Market Hedge	1,35,334
(iii)	Use of Option	1,38,700
(iv)	No hedging	1,39,100

Conclusion: Money Market Hedge is the best technique for hedging the currency risk in the above case as the outflow is least

Question 65.
A Ltd. of UK has imported some chemical worth of USD 3,64,897 from one of the U.S. suppliers. The amount is payable in six months’ time. The relevant spot and forward rates are:

Spot rate	USD 1.5617-1.5673
6 months’ forward rate	USD 1.5455 – 1.5609

The borrowing rates in U.K. and U.S. are 7% and 6% respectively and the deposit rates are 5.5% and 4.5% respectively.
Currency options are available, under which, one option contract is for GBP 12,500. The option premium for GBP at a strike price of USD1.70/GBP is USD 0.037 (call option) and USD 0.096 (put option) for 6 months period.
The Company has 3 choices:
(i) Forward cover
(ii) Money market cover, and
(iii) Currency option
Which of the alternatives is preferable by the company?
Answer:
In the given case, the exchange rates are indirect. These can be converted into direct rates as follows:
Spot rate
GBP = $\frac{1}{U S D 1.5673} / \frac{1}{U S D 1.5617}$
USD = GBP 0.63804/0.64033
6 month’s forward rate
GBP = $\frac{1}{U S D 1.5609} / \frac{1}{U S D 1.5455}$
USD = GBP0.64066/0.64704
Payoff in 3 alternatives
(i) Forward Cover
Amount payable – USD 3,64,897
Forward rate GBP – 0.64704
Payable in GBP – GBP 2,36,103 i.e. (3,64,897 × 0.64704)

(ii) Money market Cover
Since the UK importer has USD 3,64,897 payables after 6 months, the company must create an opposite situation where he has exactly USD 3,64,897 receivables after 6 months. This can be done by lending the present value of USD 3,64,897 as per the deposit rates applicable in US, which is 4.5% p.a.

Exposure and action to be taken Today
Liability	USD 3,64,897 payables after 6 months
Create	USD 3,64,897 Asset realising after 6 months
Deposit	Present Value of USD 3,64,897 at 4.5% (6 months) = $\frac{3,64,897}{1.0225}$ = USD 3,56,867.50
Amount required to get USD 3,56,867.50	Spot rate (ask): 1 USD =0.64033 Conversion Value = £2,28,512.65 (3,56,867 × 0.64033)
Borrow	£2,28,512.65@ borrowing rate in U.K i.e. 1% p.a.
Situation after 6 months
Receive	USD 3,64,897 from the deposit
Payment	Pay the exporter USD 3,64,897, received from the deposit.
Repay Loan with Int.	= 2,28,512.65 × 1.035 = £2,36,510.60
Final outflow in £	£ 2,36,510.60 (irrespective of the exchange rate)

(iii) Method-3 (Hedging using Options)
Option Contracts standard Size = GBP 12,500
Number of contracts required:
Amount in $ per contract = 12,500 × 1.70 = $21,250
Total $ payables = 3,64,897
No. of contracts = 3,64,897/21,250 = 17.17 rounded off to 17
This would cover $ 3,61,250 (21,250 × 17), thus, leaving $ 3,647 (3,64,897 – 3,61,250) un-hedged. Alternatively, a forward cover can be taken for $ 3,647. In this question, as the spot rates after 6 months are not given, the balance is covered using forward rates.
The Strike Price is 1.70 USD/GBP with a premium of $ 0.037 on call option and a premium of $0.096 on put option.
Company would take 17 contracts for 6 months (covering $ 3,61,250 at current spot rate) or GBP 2,12,500 (12,500 × 17). The call options on GBP would give right to buy GBP whereas, the need is to sell GBP against $. Therefore, Put option should be bought at a premium of 0.096$ per GBP. Therefore costs, if the options were exercised, (assuming actual rates are lower) will be:

To conclude:
Outflow under various alternatives:

S. No.	Method of Hedging	Outflow in GBP (rounded off)
(i)	Forward	2,36,103
(ii)	Money market	2,36,511
(iii)	Option contract	2,27,923

Decision: As the Outflow under option contract is least, the company should take currency option for hedging the risk.

Question 66.
An importer is due to pay the exporter on 28th January 2010, Singapore Dollars of 25,00,000 under an irrevocable letter of credit. It directed the bank to pay the amount on the due date.
Due to go-slow and strike procedures adopted by its staff, the bank was not in a position to remit the amount due. The amount was actually remitted on 4th February 2010.
On the transaction, the bank wants to retain an exchange margin of 0.125 per cent.
The following were the rates prevalent in the exchange market on the relevant dates:

	28th January	4th February
Rupee/US $1 London Pound/Dollars Pound	₹ 48.85/45.90 $ 1.7840/1.7850 Sing $ 3.1575/31590	₹ 45.91/45.97 1.7765/1.7775 Sing $3.1380/3.1390

What is the effect on account of the delay in remittance? Calculate rate in multiples of .0001. [May 2014][Nov. 2011] [5 Marks]
Answer:
The importer customer has requested to remit SGD 25 lakhs on January 28, 2010. Therefore, ask rate will be considered:

Thus, impact of strike on importer
= SGD 25,00,000 (₹ 26.0719 – ₹ 25.9806)
= ₹ 2,28,250 (Loss)
The customer will have to bear the loss of Rs.2,28,250

Question 67.
Sun Ltd. is planning to import equipment from Japan at a cost of 3,400 lakh yen. The company may avail loans at 18 per cent per annum with quarterly rests with which it can import the equipment. The company has also an offer from Osaka branch of an India based bank extending credit of 180 days at 2 per cent per annum against opening of an irrecoverable letter of credit.
Additional information:
Present exchange rate ₹ 100 = 340 yen
180 day’s forward rate ₹ 100 = 345 yen
Commission charges for letter of credit at 2 per cent per 12 months.
Advice the company whether the offer from the foreign branch should be accepted.
Answer:
Option I (To finance the purchases by availing loan at 18% per annum):

Cost of equipment

₹ in lakhs

3400 lakh yen, Spot rate: ₹ 100 = 340 yen
Add: Interest @ 4.5% I Quarter
Add: Interest @ 4.5% II Quarter (on ₹ 1045 lakhs)
Total outflow in Rupees

1,000

47.03

1,092.03

Option II (To accept the offer from foreign branch):

Advise: Option 2 is cheaper by (109203 – 1006.15) Iakh or 85.88 Iakh. Hence, the offer of letter of credit may be accepted.

Question 68.
The following market data Is available : Spot USD/JPY 116.00

Deposit rates p.a.	USD	JPY
3 months	4.50%	0.25%
6 months	5.00%	0.25%

Forward Rate Agreement (FRA) for YEN is NIL.
1. What should be 3 months FRA rate at 3 months forward ?
2. The 6 & 12 months LIBORS are 5% & 6.5% respectively. A bank is
quoting 6/12 USD FRA at 6.50 – 6.75%. Is any arbitrage opportunity available? [May 2010] [8 Marks]
Answer:
1. In USA, 3 Months Interest rate is 4.50% p.a & 6 Months Interest rate is 5% p.a.
Therefore 3 months rate are $\frac{4.5}{4}$ = 1.125% and 6 months rate are $\frac{5.0}{2}$ = 2.5%.
The forward rate for 3 months after 3 months (f) can be calculated in the following manner:
(1 + 0.01125) (1 + f) = (1 + .025)
1 + f = $\frac{1.025}{1.01125}$ = 1.01359
f = 1.01359 – 1
= 0.01359 for 3 months
Annualised forward rate = 0.01359 × 4 = 0.054388
= 5.438 p.a%

2. The 6 Months and 12 months Libor Interest rate is 5% p.a. & 12 Month interest rate is 6.5% p.a.
The forward rate for 6 months after 6 months (f) can be calculated in the ‘ following manner:
(1 + 0.025) × (1 + f ) = (1 + .065)
1 + f = $\frac{1.065}{1.025}$ = 1.3902
f = 1.03902 – 1
= 0.03902 for 6 months
Annualised forward rate = 0. 3902 × 2 = 0.07805 = 7.805 p.a%
6 Months forward 6 months rate is 7.805Q6 p.a.
The Bank is quoting 6/12 USD FRA at 6.50 – 6.75%
Since the 6 months forward rate of 7.805% is higher than the bank quotation of lending at 6.75%. Therefore there is an arbitrage opportunity of earning interest @ 7.805% p.a. & Paying @ 6.75%.
Arbitrage process:
Today, Borrow’ for 6 months @ 5%, buy an FRA & invest for 12 months @ 6.5% p.a
At the end of 12 months for $ 1 invested today will become $ 1.065
Interest cost will be @ 5% p.a for 6 months and 6.75% p.a for the balance 6 months which shall constitute the total interest as $ 1.060 at the end of 12 months for every $1 borrow ed
(1 + 0.025) (1 + 0.03375) = 1.059593 = 1.060 approx.
Since receipts will be $1,065 and cost will be $1,060, there w ill be a gain of $ 0.005.

Question 69.
Following information is given:
Exchange rate:
Canadian Dollar 0.666 per DM (spot)
Canadian Dollar 0.671 per DM (3 months)
Interest rate:
DM: 8% p.a.
Canadian Dollar :10% p.a.
To take the possible arbitrage gains, what operations would be carried out? [Nov. 2010][May 2016][May 2018 Adapted] [8 Marks]
Answer:
Step 1: Calculate the theoretical forward rates as per interest rate parity
According to Interest Rate Parity
The rate of interest in Germany – 8% per annum or 2% per 3 months
The rate of interest in Canada – 10% per annum or 2.5% per 3 months Spot rate 1 DM = Can$. 0.666
Theoretical forward rate after 3 months = Spot rate
$\left[\frac{1+\text { quarterly interest rate in Canada }}{1+\text { quarterly interest rate in Germany }}\right]^{\mathrm{t}}$
= 0.666$\left[\frac{1.025}{1.02}\right]^1$ = Can.$ 0.6692
Actual forward Rate of DM is 0.671 which is higher than theoretical rate. This means the rate of interest in Canada is less and by investing in Germany and borrowing from Canada there can be arbitrage gains. Therefore, in money market, borrow Can $
(i) Borrow Can $ 1 at 10% for 3 months
(ii) Convert into DM at spot rate $\frac{1}{0.666}$ = 1.501
(iii) Invest 1.501 DM for 3 months.
Amount received = 1.501 + (1.501 × 8% × 3/12)
= 1.501 + 0.03002 = 1.5310 DM
(iv) Sell DM forward to obtain Can $
(after three months at forward rate) = 1.5310 × 0.671
= 1.0273
(v) Repay Can $ 1 together with interest = 1.0 + (1.0 × 10% × 3/12) = 1.0250
Arbitrage Gain = 1.0273 -1.0250
= 0.0023 Can $

Question 70.
Spot rate 1 U$$ = ₹ 68.50
USD premium on a six month forward is 3%. The annualized interest in US is 4% and 9% in India.
Is there any arbitrage possibility? If yes, how a trader can take advantage of the situation if he is willing to borrow USD 3 million. [Nov. 2018 old syllabus] [8 Marks]
Answer:
SPOT 1 USD = ₹ 68.50
USD premium on 6 months forward = 3%
∴ Forward rate = 68.50 (1.03) = ₹ 70.56
The Annualized interest in US is 4% and the same is 9% in India.
According to Interest Rate Parity
Forward rate after 6 months = Spot rate $\left[\frac{1+\text { Interest rate in India }}{1+\text { Interest rate in USA }}\right]^t$
= 68.50$\left[\frac{1+0.045}{1+0.02}\right]^1$ = ₹ 70.178
Since actual forward rate is more than theoretical forward price, there is an arbitrage opportunity.

Verification of how an arbitrageur can benefit:

Step 1	Borrow Rupees in India equivalent to USD 3 million i.e. 68.50 × 3 million = ₹ 20,55,00,000
Step 2	Convert into $ @ 68.50 = $ 3 million
Step 3	Invest in US @ 4% p.a. for 6 months and take a forward cover
Step 4	After 6 months Amount received in $ with interest = 3 million × (1.02) = $ 3.06 million
Step 5	Reconvert USD into ₹ at forward rate of 70.56 = 3.06 million × 70.56 = $ 215.9136 million (inflow)
Step 6	Repay the ₹ loan together with interest = 205.5 million × 1.045 = ₹ 214.7475 million (Outflow)
Step 7	Net Gain 215.9136 – 214.7475 = ₹ 1.1661 million = ₹ 11,66,100

Question 71.
Followings are the spot exchange rates quoted at three different forex markets:

USDIINR	48.30 in Mumbai
GBPIINR	77.52 in London
GBPIUSD	1.6231 in New York

The arbitrageur has USD 1,00,00,000. Assuming that there are no transaction costs, explain whether there is any arbitrage gain possible from the quoted spot exchange rates. [Nov. 2008] [6 Marks]
Answer:
The arbitrageur can proceed as stated below to realize arbitrage gains.
(a) Buy ₹ from USD 10,000,000 at Mumbai 48.30 × 10,000,000 = ₹ 483,000,000
(b) Convert these ₹ to GBP at London $\left(\frac{\text { Rs. } 483,000,000}{\text { Rs. } 77.52}\right)$ = GBP 6,230,650.155
(c) Convert GBP to USD at New York GBP 6,230,650.155 × 1.6231 = USD 10,112,968.26
There is net gain of USD 10,112968.26 – USD 10,000,000 i.e. USD 112,968.26

Question 72.
In International Monetary Market an international forward bid for De-cember, 15 on pound sterling is $ 1.2816 at the same time the price of IMM sterling future for delivery on December, 15 is $ 1.2806. The contract size of pound sterling is £ 62,500.
How could the dealer use arbitrage in profit from this situation and how much profit is earned?
Answer:
Arbitrage is the buying and selling of the same commodity in different markets. These transactions refer to advantage derived in the transactions of foreign currencies by taking the benefit of differences in rates between two currencies at two different centres at the same time or of difference between cross rates and actual rates.

In this question:
The dealer can sell pound sterling Forward at $ 1.2816 and can buy pound sterling Futures at $ 1.2806 in International monetary market, and his arbitrage profit is calculated as follows:

Buy £62,500 @ 1.2806	$ 80037.50
Sell £ 62,500 @1.2816	$ 80100.0
Arbitrage Profit	$ 62.5
∴ The dealer can make a profit $ 62.5 per contract, through arbitrage operations

Question 73.
A Inc. and B Inc. intend to borrow $2,00,000 and $2,00,000 in ¥ respectively for a time horizon of one year. The prevalent interest rates are as follows:

Company	¥ Loan	$ Loan
A Inc	5%	9%
B Inc	8%	10%

The prevalent exchange rate is $1 = ¥120.
He entered in a currency swap under which it is agreed that B Inc will pay A Inc @ 1% over the ¥ Loan interest rate which the later will have to pay as a result of the agreed currency swap whereas A Inc will reimburse interest to B Inc only to the extent of 9%. Keeping the exchange rate invariant, quantify the opportunity gain or loss component of the ultimate outcome, resulting from the designed currency swap. [May 2011] [8 Marks]
Answer:
A and B wants to borrow the same amount in different currencies. A Inc. wants to borrow $ 2,00,000 whereas B Inc, requires $ 2,00,000 in ¥ i.e.¥
2,40,00,000, as Spot rate is $\frac{¥}{\$}$ = 120 and is not likely to change.
If A and B fulfil their requirements on their own:

Company	Applicable rate of interest
A Inc.	9%
Bine.	8%
Total cost of interest	17%

However, if A Inc. takes ¥ 2,40,00,000 and gives to B Inc. and Simultaneously, B Inc. takes $ loan and gives to A Inc. the rate of interest will be

Company	Applicable rate of interest
A Inc.	5%
B Inc.	10%
Total cost of interest	15%

Thus, there will be a net saving of 2% which can be shared by the two companies as per the arrangement.

Cash Flows of A Inc
(i) At the time of exchange of principal amount

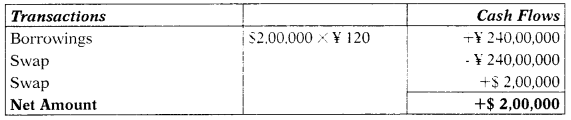
(ii) At the time of exchange of Interest amount

A Inc. used $2,00,000 at the net cost of borrowing of $16,000 i.e. 8%. if it had not opted for swap agreement the borrowing cost would have been 9%. Thus there is saving of 1%.

Cash Flows of B Inc
(i) At the time of exchange of principal amount

(ii) At the time of exchange of Interest amount

B Inc. used ¥240,00,000 at the net cost of borrowing of ¥ 16,80,000 i.e. 1%. If it had not opted for swap agreement the borrowing cost would have been 8%. Thus there is saving of 1%.

Question 74.
M/s Omega Electronic Ltd. exports air conditioners to Germany by importing all the components from Singapore. The company is exporting 2,400 units at a price of Euro 500 per unit. The cost of imported components is $800 per unit. The fixed cost and other variables cost per unit are ₹ 1,000 and ₹ 1,500 respectively. The cash flows in foreign currencies are due in six months. The current exchange rates are as follows :
₹/Euro – 51.50/55
₹/S$ – 27.20/25
After six months the exchange rates turn out as follows :
₹/Euro – 52.00/05
₹/S$ – 27.70/75
(1) You are required to calculate loss/gain due to transaction exposure
(2) Based on the following additional information calculate the loss/gain due to transaction and operating exposure if the contracted price of air conditioners is ₹ 25,000:
(i) the current exchange rate changes to
₹/Euro – 51.75/80
₹/S$ – 27.10/15
(ii) Price elasticity of demand is estimated to be 1.5
(iii) Payments and receipts are to be settled at the end of six months. [Nov. 2009] [12 Marks]
Answer:
1. Profits at current exchange rates
2400 [€500 × ₹ 51.50 – (S$ 800 × ₹ 27.25 + ₹ 1,000 + ₹ 1,500)]
2400 [₹ 25,750 – ₹ 24,300] = ₹ 34,80,000
Profit after change in exchange rates
2400 [€ 500 × ₹ 52 – (S$ 800) × ₹ 27.75 + ₹ 1,000 + ₹ 1500)]
2400 [₹ 26,000 – ₹ 24,700] = ₹ 31,20,000
Loss due to transaction exposure
34,80,0 – 7 31,20,000 = ₹ 3,60,000

2. Profit based on new exchange rates if the contracted price is Rs. 25,000
2400 [₹ 25,000- (800 ×₹ 27.15 + ₹ 1,000 + ₹ 1.500)]
2400 [₹ 25,000 – ₹ 24,220] = ₹ 18,72,000
Profit after change in exchange rates at the end of six months
2400 [₹ 25,000 – (800 × ₹ 27.75 + ₹ 1,000 + ₹ 1,500)]
2400 [₹ 25,000 – ₹ 24,700] = ₹ 7,20,000
Decline in profit due to transaction exposure
₹ 18,72,000 – ₹ 7,20,000 = ₹ 11,52,000
Current price of each unit is SS = $\frac{R s .25,000}{\text { Rs. } 51.50}$ = € 485.44
Price after change in Exch. Rate = $\frac{R s .25,000}{R s .51 .75}$ = € 483.09
Change in Price due to change in exchange rate
485.44 – 483.09 = €2.35
or (-) 0.48%
Price elasticity of demand = 1.5
Increase in demand due to fall in price 0.48 × 1.5 = 0.72%
Size of increased order = 2400 × 1.0072 = 2417 units
Profit = 2417 [T 25,000 – (800 × ₹ 27.75 + ₹ 1,500)] – Fixed costs
= 2417 [₹ 25,000 – ₹23,700] – 24,00,000 =
= 31,42,100 – 24,00,000 = ₹ 7,42,100
Therefore, decrease in profit due to operating exposure
₹ 18,72,000 – ₹ 7,42,100 = ₹ 11,29,900
Tutorial note: The fixed costs are Rs. 1000 per unit when 2400 units are sold. Therefore, the toted fixed costs shall he Rs. 24,00,000 and shall remain same irrespective of change in units sold due to increase in demand.

Question 75.
Following information relates to AKC Ltd. which manufactures some parts of an electronics device which are exported to USA, Japan and Europe on 90 days credit terms.

Foreign exchange rate information:

Advice “AKC Ltd”, (by calculating average contribution to sales ratio), whether it should hedge its foreign currency risk or not. [Nov. 2007 & 2019][8 Marks]
Answer:
If foreign exchange risk is hedged

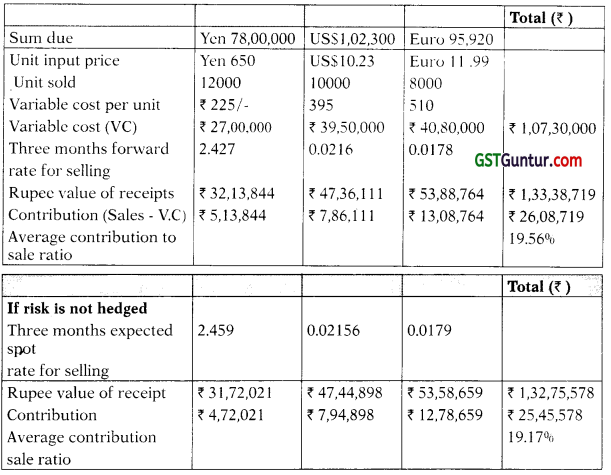
AKC Ltd. is advised to hedge its foreign currency exchange risk.

Question 76.
On 1st June 2015 the bank enters into a forward contract for 2 months for selling US$ 1,00,000 at ₹ 65.5000. On 1st July 2015 the customer demands early delivery, the spot rate was ₹ 65.7500/66.25. Calculate the amount to be debited in the customer’s account.
Answer:
The bank will apply rate originally agreed upon i.e. ₹ 65.5000 and will debit the account of the customer with ₹ 65,50,000.
The bank may accept the request of customer of delivery before the due date of forward contract provided the customer is ready to bear the loss if any that may accrue to the bank as a result of this. In addition to some prescribed fixed charges bank may also charge additional charges comprising of:
(a) Swap Difference: This difference can be loss/gain to the bank. This arises on account of offsetting its position earlier created by early delivery as bank normally covers itself against the position taken in the original forward contract.

(b) Interest on Outlay of Funds: It might be possible early delivery request of a customer may result in outlay of funds. In such cases, bank shall charge from the customer at a rate not less than prime lending rate for the period of early delivery to the original due date. However, if there is an inflow of funds the bank at its discretion may pass on interest to the customer at the rate applicable to term deposits for the same period.

Question 77.
On I October 2015 Mr. X an exporter enters into a forward contract with a BNP Bank to sell US$ 1,00,000 on 31 December 2015 at ₹ 65.40/$. However, due to the request of the importer, MR. X received amount on 28 November 2015. MR. X requested the bank the take delivery of the remittance on 30 November 2015 i.e. before due date. The inter-banking rates on 28 November 2015 was as follows:

Spot	₹ 65.22/65.27
One Month Premium	10/15

If bank agrees to take early delivery then what will be net inflow to Mr. X assuming that the prevailing prime lending rate is 18%.
Answer:
Bank will buy from customer at the agreed rate of ₹ 65.40. In addition to the same if bank will charge/pay swap difference and interest on outlay funds.

(a) Swap Difference
Bank buys at Spot Rate on 28 November 2015	₹ 65.22
Bank sells at Forward Rate of 31 December 2015 (65.27 + 0.15)	₹ 65.42
Swap Loss to the customer (per US$)	₹ 00.20
Swap loss for US$ 1,00,000	₹ 20,000
(b) Interest on Outlay Funds
On 28th November Bank buys at	₹ 65.22
It pays to the customer (5. (original rate provisionally)	₹ 65.40
Outlay of Funds per US$	₹ 00.18
Interest on Outlay fund for US$ 1,00,000 for 31 days	₹ 275.00
(US$ 1,00,000 × 00.18 × 31/365 × 18%)
(c) Charges for early delivery
Swap loss	₹ 20,000.00
Interest on Outlay fund for US$ 1,00,000 for 31 days	₹ 275.00
	₹ 20,275.00
(d) Net Inflow to Mr. X
Amount received on sale (? 65.40 × 1,00,000)	₹ 65,40,000
Less: Charges for early delivery payable to bank	₹ 20,275
	₹ 65,19,725

Question 78.
An exporter enters into a forward contract with a bank on 31.7.2018 to sell US$ 1 million to the bank on 31.12.2018. The forward rate is 1 USD = ₹ 69.50. The bank covered itself on the same day by entering into a forward contract to sell 1 million USD @ 69.65. On 28.11.2018 the exporter requests the bank to take delivery on 30.11.2018. Spot rate on 30.11.2018 is ₹ /$ 69.30/69.40. The dollar is at premium with one month swap points being 40/50. The prime lending rate is 12%. Bank charges ₹ 100 for early delivery of contract. You are required to calculate the final inflow to the exporter on 31.12.2018. Provide interest on month to month basis, ignoring days
Answer:
The bank has entered into forward buy contract with the exporter on 31.12.2018. The bank will take delivery of dollars on 30.11.2018, i.e. one month prior to the date of contract and will Dr. the customers A/c at an agreed rate of 69.50 and at the same time Cr. his account with prevailing bid rate which is ₹ 69.30. This will leave a Dr. balance in his account of ₹ 2,00,000 [10,00,000 × (69.50 – 69.30)] This will be settled at the time of maturity of the original contract along with interest. The bank will charge interest at a Prime lending rate of 12%. Secondly, the Bank will enter into an opposite forward contract to square off the original contract with the customer to sell $ 1 million on the date of maturity. Net outcome of these transactions will be settled on the date of maturity and Bank will execute both the Forward contracts.
(1) Bank will purchase $ 1 million on the spot rate of 69.30 and take a forward sell contract @ 69.90 (Spot ask rate + swap point, i.e. 69.40 + 50 points) but will pay the customer @ agreed forward rate of ₹ 69.50.
(2) Amount received by the customer on $ 1 million provisionally on the basis of original contract

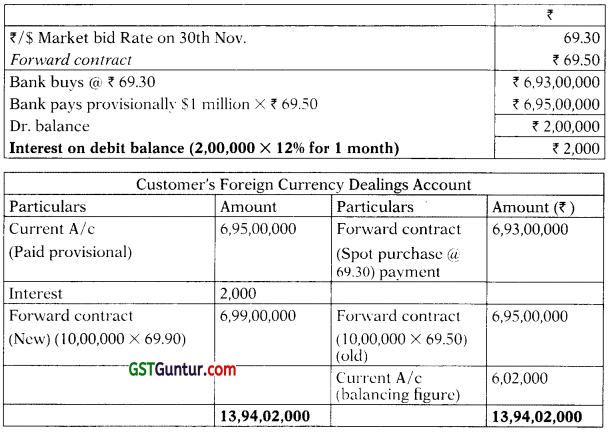
(a) Swap Difference
Bank buys at Spot Rate on 30.11.2018	₹ 69.30
Bank sells at Forward Rate of 31.12.2018	₹ 69.90
Swap Loss per US$	₹ 0.60
Swap loss for US$ 1 million	₹ 6,00,000
(b) Interest on Outlay Funds
On 30.11.2018, bank buys at	₹ 69.30
It pays to the customer provisionally	₹ 69.50
Outlay of Funds per US$	₹ 0.20
Interest on Outlay fund for 1 month	₹ 2,000
(US$ 10,00,000 × 0.20 × 1 month × 12%)
(c) Charges for early delivery	100
Swap loss	₹ 6,00,000
Interest on Outlay fund for 1 month	₹ 2,000
Total charges for early delivery	₹ 6,02,100
(d) Net inflow to Mr. the exporter
Amount received on sale (₹ 69.50 × 10,00,000)	₹ 6,95,00,000
less: Total Charges for early delivery payable to bank	₹ 6,02,100
	₹ 6,88,97,900

Question 79.
On 19th January, bank A entered into forward contract with a customer for a forward sale of US $ 7,000, delivery 20th March at ₹ 46.67. On the same day, it covered its position by buying forward from the market due 19th March, at the rate of ₹ 46.655. on 19th February, the customer approaches the bank and requests for early delivery of US $.
Rates prevailing in the interbank markets on that date are as under:
Spot (₹/$) – 46.572/46.5800
March – 46.3550/46.3650
Interest on outflow of funds is 16% and on inflow of funds is 12%.
Flat charges for early delivery are ₹ 100.
What is the amount that would be recovered from the customer on the trans-action?
Note: Calculation should be made on month’s basis than on days basis. [Nov. 2018][8 Marks]
Answer:
Bank will buy from customer at the agreed rate of ₹ 46.67. In addition to the same if bank will charge/pay swap difference and interest on outlay funds.

(a) Swap Difference
Bank sells at Spot Rate on 19th February	₹ 46.580
Bank Buys at Forward Rate of 20th March	₹ 46.355
Swap Loss per US$	₹ 0.225
Swap loss for USS 7,000	₹ 1,575
(b) Interest on Outlay Funds
On 19th Feb. bank sells at	₹ 46.58
It receives from customer provisionally	₹ 46.67
Outlay of Funds per US$	₹ 0.0900
Interest on Outlay fund for 1 month	₹ 6.300
(US$ 7000 × 0.0900 × 1 month × 12%)
(C) Charges for early delivery	100
Swap loss	₹ 1,575
Interest on Outlay fund for US$ 7000 for 1 month	(₹ 6.30)
‘Total charges for early delivery	₹ 1,668.70
(d) Net outflow of Mr. X
Amount received by Bank (₹ 46.67 × 7000)	₹ 3,26,690
Add: Total Charges for early delivery payable to bank	₹ 1,668.70
	₹ 3,28,358.70

Question 80.
On 1st January 2019 Global Ltd., an exporter entered into a forward contract with BBC Bank to sell US$ 2,00,000 on 31 st March 2019 at ₹ 71.50/ $. However, due to the request of the importer, Global Ltd. received the amount on 28 February 2019. Global Ltd. requested the Bank to take delivery of the remittance on 2nd March 2019. The Inter-banking rates on 28th February 2019 were as follows:

Spot Rate	₹ 71.20/71.25
One month premium	5/10

If Bank agrees to take early delivery then what will be the net inflow to Global Ltd. assuming that the prevailing prime lending rate is 15%. Assume 365 days in a Year. [May 2019] [8 Marks]
Answer:
Here, Global Ltd. approaches the Bank for early delivery on 2nd March, the Bank has made a forward purchase of US$ 2,00,000 due on 3 1st March 2019 at ₹ 71.50 per $, the Bank will purchase $ on spot basis on 2nd March i.e. ₹ 71.20 Per $ but will pay to Global Ltd. @ 71.50 i.e. the rate of original forward contract on the provisional basis. This will lead to a debit balance in the Global Ltd. A/c with bank. This will be settled at the time of maturity of the original contract along with interest. The bank will charge interest @ 15% for 31 days. Secondly, the Bank will enter into an opposite forward contract to square off the original contract with the customer to sell $ 2,00,000 on the date of maturity. Net outcome of these transactions will be settled on the date of maturity and Bank will execute both the Forward contracts.

Purchase of $ 2,00,000 on the spot rate of 71.20 and sell forward contract @ 71.35 due on 31st March 2019.

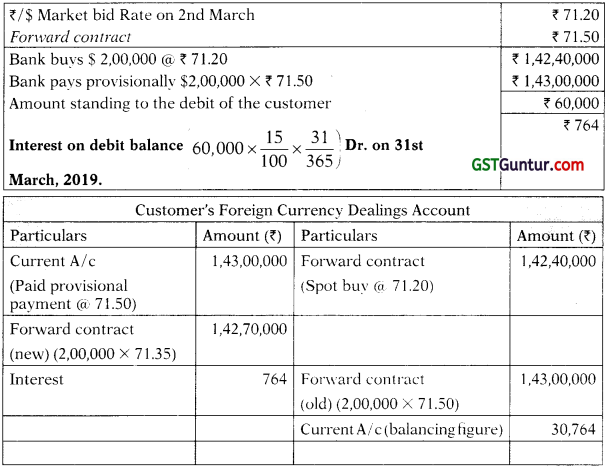
Alternative Solution:
Bank will buy from customer at the agreed rate of ₹ 71.50. In addition to the same, bank will charge/pay swap difference and interest on outlay funds.

(a) Swap Difference:
Bank buys at Spot Rate on 2nd March	₹ 71.20
Bank sells at Forward Rate of 31st March	₹ 71.35
Swap Loss to Global Ltd. (per US$)	₹ 0.15
Swap loss for US $ 2,00,000	₹ 30,000
(b) Interest on Outlay Funds:
On 2nd March bank buys at	₹ 71.20
It pays to Global Ltd.	₹ 71.50
Outlay of Funds per US$	₹ 0.30
Total Outlay ol funds	₹ 60,000
(US$ 2,00,000 × 0.30 × 31 days × 15°o)	₹ 764
(c) Total Charges:
Swap loss	₹ 30,000
Interest on Outlay fund	₹ 764
Total charges for early delivery	₹ 30,764
(d) Net inflow to Global Ltd.:
Amount received on sale (₹ 71.50 × 2.00,000)	₹ 1,43,00,000
Less: Total Charges for early delivery payable to bank	₹ 30,764
	₹ 1,42,69,236

Question 81.
A customer with whom the Bank had entered into 3 months forward purchase contract for Swiss Francs 1,00,000 at the rate of ₹ 36.25 comes to the bank after two months and requests cancellation of the contract. On this date, the rates are:

Spot	CHF 1 = ₹ 36.30	36.35
One month forward	36.45	36.52

Determine the amount of Profit or Loss to the customer due to cancellation of the contract.
Answer:
Original contract for CHF 1,00,000 @ 36.25 – amount receivable by the customer to cancel the purchase contract 1 month before the due date – The contract will be cancelled at 1 month forward ask rate i.e. CHF 1 = ₹ 36.52 payable by the customer.
Hence, swap profit/loss to the customer:

Particulars	Calculation	Amount ₹
Payable by the customer	₹ 36.52 × 1,00,000 (Forward sale by bank for cancellation)	36,52,000
Receivable by the customer	₹ 36.25 × 1,00,000 (Original Purchase by bank)	36,25,000
Therefore, total loss to the customer	₹ 0.27 × 1,00,000 (36.52 – 36.25)	27,000

Question 82.
On 15th January 2015 you as a banker booked a forward contract for US$ 2,50,000 for your import customer deliverable on 15th March 2015 at ₹ 65.3450. On due date customer request you to cancel the contract. On this date quotation for US$ in the inter-bank market is as follows:

Spot	₹ 65.2900/2975 per US$
Spot/ April	3000/3100
Spot /May	6000/6100

Assuming that the flat charges for the cancellation is ₹ 100 and exchange margin is 0.10%, then determine the cancellation charges payable by the customer.
Answer:
Since this is sale contract, the contract shall be cancelled at ready buying rate on the date of cancellation as follows:

	₹
Spot Buying Rate on 15 March 2015	65.2900
Less: Exchange Margin	0.0653
	65.2247
Rounded to	65.2250
Dollar sold to customer at	65.3450
Dollar bought from customer	65.2250
Net amount payable by the customer per US$	0.1200
Total Amount payable by the customer:
Flat Charges
Cancellation Charges (₹ 0.12 × 2,50,000) =	100
	30,000
	30,100

Question 83.
You as a banker has entered into 3 months’ forward contract with your customer to purchase and 1,00,000 at the rate of ₹ 47.2500. However after 2 months your customer comes to you and requests cancellation of the contract. On this date quotation for AUD in the market is as follows:

Spot	₹ 47.3000/3500 per AUD
1 month forward	₹ 47.4500/5200 per AUD

Determine the cancellation charges payable by the customer.
Answer:
The contract shall be cancelled at the 1 month forward sale rate of ₹ 47.5200 as follows:

AUD bought from customer under original forward contract at	₹ 47.2500
On cancellation it is sold to him at	₹ 47.5200
Net amount payable by customer per AUD	₹ 00.2700
Thus total cancellation charges payable by the customer	₹ 27,000

Question 84.
A hank enters into a forward purchase TT covering an export bill for Swiss Francs 25000 at ? 32.4000 due on 25th April and covered itself for same delivery in the local interbank market at ₹ 32.4200. However, on 25th March, exporter sought for cancellation of the contract as the tenor of the bill is changed.
Swiss Francs were quoted against US dollars as under:
Spot USD 1 = Sw. Fes. 1.5076/1.5120
One month forward 1.5150/1.5160
Two months forward 1.5250/1.5270
Three months forward 1.5415/1.5445
And in the interbank market US dollars were quoted as under:
Spot USD 1 = ₹ 49.4302/.4455
Spot /April (swap points) .4100/ .4200
Spot/May .4300/.4400
Spot/June .4500/.4600
Calculate the cancellation charges, payable by the customer if exchange margin required by the bank is 0.10% on buying and selling.
Answer:
First the contract will be cancelled at TT Selling Rate
(i) Determination of TT Selling Rate:

(ii) Calculation of Cancellation charges
Bank buys Sw. Fes. Under original contract = ₹ 32.4000
Bank Sells under Cancellation = ₹ 32. 9475
Difference payable by customer = ₹ 00.5475

Exchange difference of Sw. Fes. 25,000 payable by (Sw. Fes. 25,000 × ₹ 0.5475)

Question 85.
Suppose you are a banker and one of your export customer has booked as US$ 1,00,000 forward sale contract for 2 months with you at the rate of ₹ 62.5200 and simultaneously you covered yourself in the interbank market at 62.5900. However on due date, after 2 months your customer comes to you and requests for cancellation of the contract and also request for extension of the contract by one month. On this date quotation for US$ in the market was as follows:

Spot	₹ 62.6800/62.7200
1 month forward	₹ 62.6400/62.7400

Determine the extension charges payable by the customer assuming exchange margin of 0.10% on buying as well as selling. (Round off in multiples of 0.0025)
Answer:
Cancellation
First the original contract shall be cancelled as follows:

	₹
US$/₹ Spot Selling Rate	62.7200
Add: Margin @ 0.10%	0.06272
Net amount payable by customer per US$	62.7827
Rounded off	62.7825
Bank buys US$ under original contract at	62.5200
Difference	0.2675
Thus total cancellation charges payable by the customer for US$ 1,00,000	₹ 26,750
Rebooking or extension rate
Forward US$/₹ Buying Rate	62.6400
Less: .Margin @ 0.10%	0.06264
Net amount payable by customer per US$	62.57736
Rounded off	62.5775

Question 86.
An importer booked a forward contract with his bank on 10th September for USD 5,00,000 due on 10th December 2017 @ ₹ 68.2500. The bank covered its position in the market at ₹ 67.8000.
The exchange rates for dollar in the interbank market on 10th December and 20th December were:

	10th December	20th December
Spot USD 1 =	₹ 67.5000/67.5800	₹ 67.7000/67.8000
Spot/December	₹ 67.9200/9500	₹ 68.8000/8500
March 2018	₹ 70.2500/70.5000	₹ 70.4500/7500

Exchange margin 0.10% and interest on outlay of funds @ 12%. The importer requested on 20th December for extension of contract with due date on 10th March 2018. Rates rounded to 4 decimal in multiples of 0.0025.
On 10th December, Bank Swaps by selling spot and buying one month forward. Calculate:
(i) Cancellation rate
(ii) Amount payable on $ 5,00,000
(iii) Swap loss
(iv) Interest on outlay of funds, if any
(v) New contract rate
(vi) Total Cost [Practice Question]
Answer:
(i) Cancellation Rate
The forward sale contract shall be cancelled at Spot TT Purchase for $ prevailing on the date of cancellation as follow s:

$/₹ Market Buying Rate	₹ 67.7000
Less: Exchange Margin @ 0.10%	₹ 0.0677
	₹ 67.6323

Rounded off to ₹ 67.6325

(ii) Amount payable on $ 5,00,000

Bank sells $ 5,00,000 @ ₹ 68.25	₹ 3,41,25,000
Bank buys $ 5,00,000 @ ₹ 67.6325 (rounded off figure is used)	₹ 3,38,16,250
Amount payable by customer	₹ 3,08,750

(iii) Swap loss
On 10th December the bank does a swap sale of $ at market buying rate of 67.5000 and forward purchase for December at market selling rate of 67.9500

Bank buys at	67.9500
Bank sells at	67.5000
Amount payable by customer per $	0.4500
Total amount payable (5,00,000 × 0.4500)	₹ 2,25,000

(iv) Interest on Outlay of Funds
On 10th December the bank receives delivery under cover contract at ₹ 67.80 and sell spot at ₹ 67.50.

Bank buys at	₹ 67.8000
Bank sells at	₹ 67.5000
Difference	₹ 0.3000

Outlay for $ 5,00,000 in ₹ =1,50,000
Interest on ₹ 1,50,000 @ 12% for 10 days ₹ 500 (approx.)

(v) New Contract Rate
The contract will be extended at current rate

$/₹ Market forward selling Rate for March 2018	₹ 70.7500
Add: Exchange Margin @ 0.10%	₹ 0.0775
	₹ 70.82075

Rounded off to ₹ 70.8200

(vi) Total Cost

Cancellation Charges	₹ 3,08,750
Swap Loss	₹ 2,25,000
Interest	₹ 500
	5,34,250

Question 87.
On 10th July, an importer entered into a forward contract with bank for US$ 50,000 due on 10th September at an exchange rate of ₹ 66,8400. The bank covered its position in the interbank market at ₹ 66.6800.
How the bank would react if the customer requests on 20th September:
(i) to cancel the contract?
(ii) to execute the contract?
(iii) to extend the contract with due date to fall on 10th November? The/exchange rates for US$ in the interbank market were as below:

	10th September	20th September
Spot US$ 1 =	66.1500/1700	65.9600/9900
Spot/September	66.2800/3200	66.1200/1800
Spot/October	66.4100/4300	66.2500/3300
Spot/November	66.5600/6100	66.4000/4900

Exchange margin was 0.1% on buying and selling.
Interest on outlay of funds was 12% p.a.
You are required to show the calculations to:
(i) cancel the Contract,
(ii) execute the Contract, and
(iii) extend the Contract as above. [Nov. 2016] [8 Marks]
Answer:
As per the FEADI Rule of Automatic Cancellation the customer shall pay the charges consisting of the following:
(a) Exchange Difference
(b) Swap Loss
(c) Interest on Outlay Funds
(a) Exchange Difference
(1) Cancellation Rate
The forward sale contract shall be cancelled at Spot TT Purchase for $ prevailing on the date of cancellation as follows:

$/₹ Market Buying Rate	₹ 65.9600
Less: Exchange Margin @ 0.10%	₹ 0.0660
	₹ 65.8940

(2) Amount payable on $ 50,000

Bank sells $ 50,000 @ ₹ 66.8400	₹ 33,42,000
Bank buys $50,000 @ ₹ 65.8940	₹ 32,94,700
Amount payable by customer	₹ 47,300

(b) Swap loss
On 10th September the bank does a swap sale of $ at market buying rate of 66.3200 and forward purchase for September at market selling rate of 66.1500

Bank buys at $ 50,000 @	₹ 66.3200
Bank sells at $50,000 @	₹ 66.1500
Amount payable by customer per $	0.1700
Total ($ 50,000 × 0.1700)	₹ 8,500

Bank buys at	₹ 66.6800
Bank sells at	₹ 66.1500
Amount payable by customer	₹ 0.5300

Outlay for $ 50,000 in ₹ 26,500
Interest on ₹ 26,500 @ 12% for 10 days ₹ 87

(d) Total Cost

Cancellation Charges	₹ 47,300.00
Swap Loss	₹ 8,500.00
Interest	₹ 87.00
	₹ 55,887.00

(e) New Contract Rate
The contract will be extended at current rate

$/₹ Market forward selling Rate for November	₹ 66.4900
Add: Exchange Margin @ 0.10%	₹ 0.0665
	₹ 66.5565

(i) Charges for Cancellation of Contract = ₹ 55,887

(ii) Charges for Execution of Contract

(iii) Charges for Extension of Contract

Charges for Cancellation of Contract	₹ 55,837
New Forward Rate	₹ 66.5565

Question 88.
An importer requested his bank to extend for Forward contract of US $ 25,000 which is due for maturity on 31-10-2015 for a further period of six months. The other details are as under:
Cohtract rate US $ 1 = ₹ 61.000
The US $ quoted on 31-10-2015
Spot: ₹ 60.3200/60.6300
Six months premium : 086%/0.98%
Margin money for buying and selling rate are 0.086% and 0.15% respectively.
Compute:
(1) Cost to importer in respect to extension of forward contract.
(2) New Forward contract rate. [May 2017] [6 Marks]
Answer:
(i) Calculation of cost to Importer
The contract is to be cancelled on 31/10/2015

Cost to importer = 25,000 × (60.2681 – 61)
= 15,06702 – 15,25,000
= (Rs. 18,298)

(ii) Calculation of New Forward Contract Rate

Question 89.
A bank enters into a forward purchase TT covering an export bill for Swiss Francs 1,00,000 at ₹ 32.4000 due on 25th April and covered itself for same delivery in the local interbank market at ₹ 32.4200. However, on 25th March, exporter sought for cancellation of the contract as the tenor of the bill is changed.
In Singapore market, Swiss Francs were quoted against US dollars as under:
Spot USD 1 = Sw. Fcs1.- 5076/1.5120
One month forward – 1.5150/1.5160
Two months forward – 1.5250/1.5270
Three months forward – 1.5415/1.5445
And in the interbank market US dollars were quoted as under:

Calculate the cancellation charges, payable by the customer if exchange margin required by the bank is 0.10% on buying and selling. [Nov. 2015][5 Marks]
Answer:
First the contract will be cancelled at TT Selling Rate

Exchange difference of Sw. Fes. 1,00,000 payable by customer ₹ 54,750 (Sw. Fes. 1,00,000 × ₹ 0.5475)

Question 90.
An importer booked a forward contract with his bank on 10th April for USD 2,00,000 due on 10th June @ ₹ 64.4000. The bank covered its position in the market at ₹ 64.2800.
The exchange rates for dollar in the interbank market on 10th June and 20th June were:

	10th June	20th June
Spot USD 1 =	₹ 63.8000/8200	₹ 63.6800/7200
Spot/June	₹ 63.9200/9500	₹ 63.8000/8500
July	₹ 64.0500/0900	₹ 63.9300/9900
August	₹ 64.3000/3500	₹ 64.1800/2500
September	₹ 64.6000/6600	₹ 64.4800/5600

Exchange margin 0.10% and interest on outlay of funds @ 12%. The importer requested on 20th June for extension of contract with due date on 10th August. Rates rounded to 4 decimal in multiples of 0.0025.
On 10th June, Bank Swaps by selling spot and buying one month forward.
Calculate:
(i) Cancellation rate
(ii) Amount payable on $ 2,00,000
(iii) Swap loss
(iv) Interest on outlay of funds, if any
(v) New contract rate
(vi) Total Cost [May 2015] [Nov. 2015] [9 Marks]
Answer :
(i) Cancellation Rate
The forward sale contract shall be cancelled at Spot TT Purchase for $ prevailing on the date of cancellation as follows:

$/₹ Market Buying Rate	₹ 63.6800
Less: Exchange Margin @ 0.10%	₹ 0.0636
	₹ 63.6800

Rounded off to Rs. 63.6175

(ii) Amount payable on $ 2,00,000

Bank sells $ 2,00,000 @ ₹ 64.4000	₹ 1,28,80,000
Bank buys $2,00,000 @ ₹ 63.6175 (rounded off figure is used)	₹ 1,27,23,500
Amount payable by customer	₹ 1,56,500

(iii) Swap loss
On 10th June the bank does a swap sale of $ at market buying rate of 63.8000 and forward purchase for June at market selling rate of 63.9500

Bank buys at	63.9500
Bank sells at	63.8000
Amount payable by customer per $	0.1500
Total amount payable (2,00,000 × 0.1500)	₹ 30,000

(iv) Interest on Outlay of Funds
On 10th June the bank receives delivery under cover contract at ₹ 64.2800 and sell spot at ₹ 63.8000.

Bank buys at	₹ 64.2800
Bank sells at	₹ 63.8000
Amount payable by customer	₹ 0.4800

Outlay for $ 2,00,000 in ₹ = 96,000
Interest on ₹ 96,000 @ 12% for 10 days ₹ 320 (Assuming 360 days in a year)

(v) New Contract Rate
The contract will be extended at current rate

$/₹ Market forward selling Rate for August	₹ 64.2500
Add: Exchange Margin @ 0.10%	₹ 0.0643
	₹ 64.3143

Rounded off to ₹ 64.3150

(vi) Total Cost

Cancellation Charges	₹ 1,56,500.00
Swap Loss	₹ 30,000.00
Interest	₹ 320.00
	₹ 1,86,820.00

Question 91.
Y has to remit USD $ 1,00,000 for his son’s education on 4th April, 2018. Accordingly, he has booked a forward contract with his bank on 4th January @ ₹ 63.8775. The bank covered its position in the market at ₹ 63.7575.
The exchange rates for US$ in the interbank market on 4th April and 14th April were:

	4th April ₹	14th April ₹
Spot USD 1 =	63.2775/63.2975	63.1575/63.1975
Spot/March	63.3975/63.4275	63.2775/63.3275
April	63.5275/63.5675	63.4075/63.7650
May	63.7775/63.8250	63.6575/63.7275
June	64.0700/64.1325	63.9575/64.0675

Exchange margin 0.10 per cent and interest on outlay of funds @12 per cent are applicable. The remitter due to rescheduling of the semester, has requested on 14th April, 2018 for extension of contract with due date on 14th June, 2018.
Rates must be rounded to 4 decimal in multiples of 0.0025.
Calculate:
(i) Cancellation rate
(ii) Amount payable on $ 1,00,000
(iii) Swap loss
(iv) Interest on outlay of funds, if any
(v) New contract rate
(vi) Total Cost [May 2018] [8 Marks]
Ans.:
(i) Cancellation Rate
The forward sale contract shall be cancelled at Spot TT Purchase for prevailing on the date of cancellation as follows:

$/C Market Buying Rate	₹ 63.1575
Less: Exchange Margin @ 0.10%	₹ 0.0631
	₹ 63.0944

Rounded off to ₹ 63.0950

(ii) Amount payable on $ 1,00,000

Bank sells $ 1,00,000 @ ₹ 63.8775	₹ 63,87,750
Bank buvs $1,00,000 @ ₹ 63.0950 (rounded off figure is used)	₹ 63,09,500
Amount payable by customer	₹ 78,250

(iii) Swap loss
Bank Swaps by selling spot and buying one month forward.

Bank buys at	63.4275
Bank sells at	63.2775
Amount payable by customer per	0.1500
Total amount payable (1,00,000 × 0.1500)	₹ 15,000

(iv) Interest on Outlay of Funds
On 4th April the bank receives delivery under cover contract at ₹ 63.7575 and sell spot at ₹ 63.2775.

Bank buys at	₹ 63.7575
Bank sells at	₹ 63.2775
Difference	₹ 0.4800

Outlay for $ 1,00,000 in ₹ = 48,000
Interest on ₹ 48,000 @ 12% for 10 days = ₹ 158 (approx..) (Assuming 365 days in a year)

(v) New Contract Rate
The contract will be extended at current rate

$/₹ Market forward selling Rate for June 2018	₹ 64.0675
Add: Exchange Margin @ 0.10°%	₹ 0.0641
	64.1316

Rounded off to ₹ 64.1325

(vi) Total Cost

Cancellation Charges	₹ 78,250
Swap Loss	₹ 15,000
Interest	₹ 158
	93,408

Question 92.
Following are the details of cash inflows and outflows in foreign currency denominations of MNP Co. an Indian export firm, which have no foreign subsidiaries:

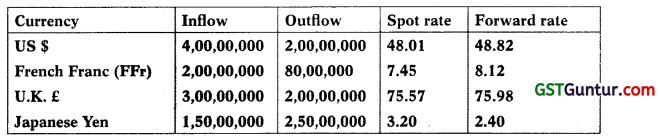
(i) Determine the net exposure of each foreign currency in terms of Rupees,
(ii) Are any of the exposure positions offsetting to some extent? [Nov. 2006][4 Marks]
Answer:
(i) Net exposure of each foreign currency in Rupees

(ii) The exposure of Japanese yen position is being offset by a better forward rate.

Question 93.
NP and Co. has imported goods for US $ 7,00,000. The amount is payable after three months. The company has also exported goods for US $ 4,50,000 and this amount is receivable in two months. For receivable amount a forward contract is already taken at ₹ 48.90.
The market rates for ₹ and Dollar are as under :
Spot – ₹ 48.50/70
Two months – 25/30 points
Three months – 40/45 points
The company wants to cover the risk and it has two options as under:
(A) To cover payables in the forward market and
(B) To lag the receivables by one month and cover the risk only for the net amount. Mo interest for delaying the receivables is earned.
Evaluate both the options if the cost of Rupee Funds is 12%. Which option is preferable? [May 2012] [8 Marks]
Answer:
(i) Coverage of payable and receivable in forward Market

(ii) Lag the receivables:

Since net payable amount is less in case of first option, hence the company should honour the forward contract after 2 months and receive interest for 1 month to find the net payment after 3 months.

Note: Since the forward contract for receivable was already booked it has to be cancelled if the receivables are lagged. Accordingly any profit/loss on cancellation of contract shall also be calculated and shall be adjusted:

In the question it has not been clearly mentioned that whether quotes given for 2 and 3 months (in points terms) are premium points or direct quotes. The solution is based as they are swap points and as they are in ascending order, the $ is at premium and points are added to the spot rate to find the applicable forward rates.

Question 94.
A inc. has imported goods for GBP 5,00,000. The amount is payable after three months. The company has also exported goods for GBP 3,50,000 but this amount is receivable in two months. For receivable amount a forward contract is already taken at ₹ 81.45.
The market rates for ₹ and GBP are as under :
Spot – ₹ 81.20/70
Two months swap – 25 / 30 points
Three months swap – 40/45 points
The company wants to cover the risk and it has two options as under:
(a) To cover payables in the forward market and
(b) To lag the receivables by one month and cover the risk only for the net amount. No interest for delaying the receivables is earned.
Evaluate both the options if the cost of Rupee Funds is 12%. Which option is preferable? [Practice Question]
Answer:
(a) Coverage of payable and receivable in forward Market

(b) Lag the receivables

Since net payable amount is less in case of first option, hence the company should honour the forward contract after 2 months and receive interest for 1 month to find the net payment after 3 months.

Working Note 1 (W.N.1) :
Cancellation rate: Since the forward bid is cancelled the exporter will have to buy from the market at 2 months ask rate, which is 82.00 (81.70 + 30 swap points)

Question 95.
Suppose that covered after tax, lending and borrowing rates for three units of Zenith pic. located in the United States, France and Germany are:

	Lending (%)	Borrowings (%)
United States	3.1	3.9
France	3.0	4.2
Germany	3.2	4.4

Currently, the French and the German units owe $ 3 million and $ 2 million, respectively to their US parent. The German unit also has $ 1 million is payables outstanding to its French affiliate. The timing of these payments can be changed by up to 90 days in either direction. Assume that Zenith US is borrowing funds while both the French and the German subsidiaries have excess cash available.
(i) What is Zenith’s optimal leading and lagging strategy?
(ii) What is the net profit impact of these adjustments? [Practice Question]
Answer:
(i) Both subsidiaries should speed up their payments to the parent while the German unit should lag its payments to the French firm.

(ii) The net effect of these adjustments is that Zenith U.S. reduces its borrowing by $ 5 million, the French unit has $ 3 million and the German unit has $ 2 million less in cash The U.S. interest expense is reduced by $ 48,750 ($ 5 million @ 3.9% for 90 days) while German and French interest income are reduced by $ 16,000 ($2 million (a 3.2% for 90 days) and $ 22,500 ($ 3 million @ 3.0% for 90 days), respectively. So there is a net savings of $ 10,250 [48,750 – (16,000 22,500)]. By delaying payment to the French
affiliate the German can earn interest of 0.2% above the French rate. This will give additional benefit of $500 ($1 million @ 0.2% for 90 days).

Question 96.
Your bank’s London office has surplus funds to the extent of USD 5,00,000/- for a period of 3 months. The cost of the funds to the bank is 4% p.a. It proposes to invest these funds in London, New York or Frankfurt and obtain the best yield, without any exchange risk to the bank. The following rates of interest are available at the three centres for investment of domestic funds there for a period of 3 months.
London – 5% p.a.
New York – 8% p.a.
Frankfurt – 3% p.a.
The market rates in London for US dollars and Euro are as under: London on New York
Spot – 1.5350/90
1 month – 15/18
2 month – 30/35
3 month – 80/85
London on Frankfurt
Spot – 1.8260/90
1 month – 60/55
2 month – 95/90
3 month – 145/140
At which centre, will the investment be made & what will be the net gain (to the nearest pound) to the bank on the invested funds?[Nov. 2013] [8 Marks]
Answer:

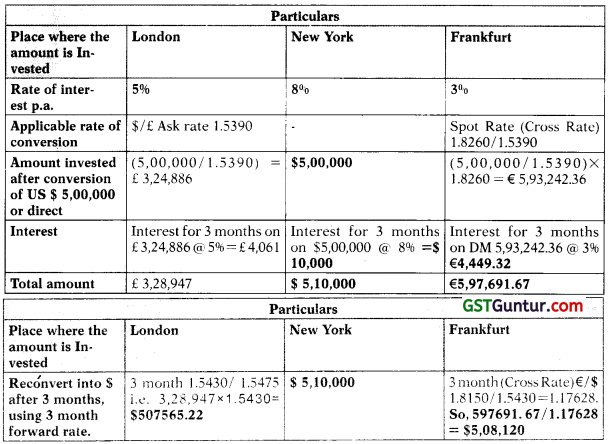
Decision: Investment made in New York yields maximum profit. Hence it should be opted for. The cost of funds will remain same @ 4% therefore, after repaying $ 5,05,000, US is best.
Note: The forward rates given are swap points, otherwise they could not have been in descending order.

Question 97.
KGF bank’s Sydney branch has surplus funds of USD 7,00,000 for a period of 2 months. The cost of the funds to the bank is 6% p.a. They propose to invest these funds in Sydney, New York or Tokyo and obtain the best yield, without any exchange risk to the bank. The following rates of interest are available at the three centres for investment of domestic funds there for a period of 2 months.
Sydney – 7.5% p.a.
New York – 8% p.a.
Tokyo – 4% p.a.
The market rates in Australia for US dollars and Yen are as under:
Sydney on New York
Spot – 0.7100/0.7300
1 month – 10/20
2 month – 25/30
Sydney on Tokyo
Spot – 79.0900/79.2000
1 month – 40/30
2 month – 55/50
At which centre, will the investment be made & what will be the net gain to the bank on the invested funds? [May 2019] [8 Marks]
Answer:

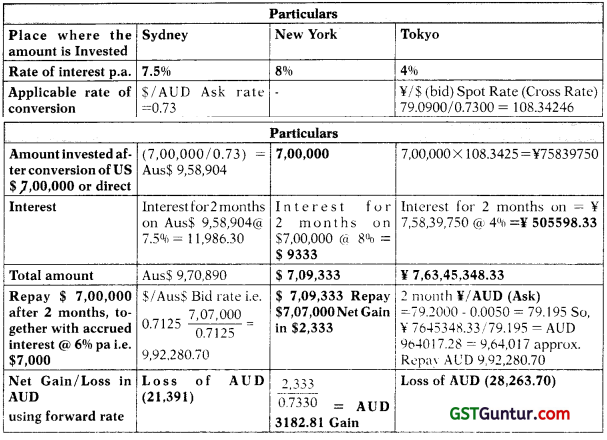
Decision: Investment made in New York yields maximum profit. Hence it should be opted for.
Tutorial Note:
(1) Tutorial the forward rates given are swap points, otherwise they could not have been in descending order.
(2) In case of investment made in Tokyo, the suggested answer as per ICAI is loss of AUD 30,353. Whereas the same is loss of AUD 28,263.70 in our solution. The difference is due to the fact that ICAI has taken exchange rate upto 2 digits after decimal whereas our answer is based on 4 digits after decimal.

Question 98.
The treasury desk of a global bank incorporated in UK wants to invest GBP 200 million on 1st January, 2019 for a period of 6 months and has the following options:
(1) The Equity Trading desk in Japan wants to invest the entire GBP 200 million in high dividend yielding Japanese securities that would earn a dividend income of JPY 1,182 million. The dividends are declared and paid on 29th June. Post dividend, the securities are expected to quote at a 2% discount. The desk also plans to earn JPY 10 million on a stock borrow lending activity because of this investment. The securities are to be sold on June 29 with a T+l settlement and the amount remitted back to the treasury in London.

(2) The fixed income desk of US proposed to invest the amount in 6 month g-secs that provides a return of 5% p.a.
The exchange rates are as follows:

Currency pair	1 Jan-2019 (spot)	30 June-2019 (forward)
GBY-JPY	148.0002	150.0000
GBP-USD	1.28000	1.30331

As a treasurer, advise the bank on the best investment option. What would be your decision from a risk perspective. You may ignore taxation. [Nov. 2018] [8 Marks]
Answer:
The treasury desk of a global bank incorporated in UK wants to invest GBP = 200 million on 1st January, 2019 for 6 months under the following two options:

Option-1
Investment in Japanese Securities = 200 million GBP
Given = Spot
GBP-JPY = 148.0002
∴ Investments = 29600.04 millions JPY
After 6 months return = 1182 million
Earnings on stock borrow lending = 10 million
As the investments are expected to quote at a 2% discount, post (Original – 2%)
dividends the Value of investment = 29600.04 – 2% = 29008.0392
Total ¥ (Investment + Dividends + earnings) = 30200.0392 million
Value in GBP = 30200.0392
(Using forward rate) 150
Amount remitted back to Treasury in under = £ 201.33359

Option – 2
Investment in 6 months G. Secs. @ 5% p.a. in U.S. 200 millions GBP
Spot GBP-USD = 1.28
USD = 256 million
Return @ 5% p.a. = 2.5% for 6 months = 6.4
Total USD = 262.4 million
Convert into GBP = 201.3335277
(Using forward rate GBP – USD =1.30331)
It is advisable to invest in US as the return is more or less same but by investing in US, as far as risk perspective is concerned, Govt. Securities are safer. Therefore, with same return and less risk investments should be made in US securities.

Question 99.
AMK Ltd. an Indian based company has subsidiaries in U.S. and UK Forecasts of surplus funds for the next 30 days from two subsidiaries are as below:
U.S. – $12.5 million
U.K. – £ 6 million
Following exchange rate information is obtained:

	$/₹	£/₹
Spot	0.0215	0.0149
30 days forward	0.0217	0.0150

Annual borrowing/deposit rates (Simple) are available.
₹ 6.4%/6.2%
$ 1.60/1.5%
£ 3.90/3.7%
The Indian operation is forecasting a cash deficit of ₹ 500 million.
It is assumed that interest rates are based on a year of 360 days.
(i) Calculate the cash balance at the end of 30 days period in (for each company under each of the following scenarios ignoring transaction costs and taxes:
(a) Each company invests/finances its own cash balances/deficits in local currency independently.
(b) Cash balances are pooled immediately in India and the net balances are Invested/borrowed for the 30 days period.
(ii) Which method do you think is preferable from the parent company’s point of view?
Answer:
Cash Balances:
(i) (a) Acting independently

	Capital	Interest	₹ in 30 days
India	-5,00,000	2,666.67	-5,02.667
U.S.	12,500	15.63	5,76,757
U.K.	6,000	18.50	4,01 ,233
			4,75,323

Cash Balances:
(b) Immediate Cash pooling

₹ 4,84,080 will be invested in India @ 6.2% for 30 days. Interest
= 484,080 × $\frac{6.2}{100}$ × $\frac{30}{360}$ = 2501
Final cash balance at the end of 30 days = 484080

(ii) Immediate cash pooling is preferable as it maximizes interest earnings.
Note: If the company decides to invest pooled amount of ₹ 4, 84,080 @ 6.2% p.a. for 30 days an interest of ₹ 2, 501 will accrue.

Question 100.
XYZ Bank, Amsterdam, wants to purchase ₹ 25 million against £ for funding their Nostro account and they have credited LORO account with Bank of London, London.
Calculate the amount of £’s credited. Ongoing inter-bank rates are per $, ₹ 61.3625/3700 & per £, $ 1.5260/70. [Nov. 2013] [4 Marks]
Answer:
To purchase Rupee, XYZ Bank shall first sell £ and purchase $ and then sell $ to purchase ₹. Accordingly, following rate shall be used: (£/₹) ask.
The rates available are:
($/£) = $ 1.5260
($/£) = $ 1.5270
(₹/$) = ₹ 61.3625
(₹/$) = ₹ 61.3700
From above available rates we can compute required rate as follows:
(£/₹)_ask = (£/$)_ask × ($/₹)_ask
= (1/1.5260) × (1/61.3625)
= £ 0.01068 or £0.0107
Thus amount of £ to be credited
= ₹ 25,00,000 × £ 0.0107
= £ 2,67,500

Question 101.
A dealer in foreign exchange has the following position in Swiss Francs on 31st January, 2018.

Particulars	(Swiss Francs)
Balance in the NOSTRO A/c Credit	1,00,000
Opening position overbought	50,000
Purchased a bill on Zurich	70,000
Sold forward TT	49,000
Forward purchase contract cancelled	41,000
Remitted by TT	75,000
Draft on Zurich cancelled	40,000

Examine what steps would the dealer take, if he is required to maintain a credit balance of Swiss francs 30,000 in the NOSTRO A/c and keep as overbought position on Swiss francs 10,000 [Nov. 2018] [8 Marks]
Answer:
Exchange Position/currency position

	Purchase £	Sale £
Opening Balance Overbought	35,000	–
DD Purchased	12,500	–
Purchased a Bill on London	40,000	–
Sold forward TT	–	30,000
Forward purchase contract cancelled	–	15,000
TT Remittance		37,500
Draft on London cancelled	15,000	–
	1,02,500	82,500
Closing Balance Overbought	–	20,000
	1,02,500	1,02,500

The Bank has to buy spot TT S\v. Fcs. 5,000 to increase the balance in Nostro account to Sw. Fcs. 30,000. This would bring down the oversold position on Sw. Fcs. as Nil. Since the bank requires an overbought position of Sw. Fcs. 10,000, it has/to buv forw’ard Sw. Fcs. 10,000

Question 102.
A dealer in foreign exchange has the following position in Swiss francs on 31st January, 2018.

Particulars	Purchase Sw. Fcs	Sale Sw. Fcs
Opening Balance Overbought	50,000
Bill on Zurich	70,000
Forward Sales – TT		49,000
Cancellation of Forward Contract		41000
TT Sales		75,000
Draft on Zurich cancelled	40,000
Closing Balance Oversold	5,000
	1,65,000	1,65,000
Cash Position (Nostro A/c)	Credit	Debit
Opening balance credit .	1,00,000
TT sales		75,000
	1,00,000	75,000
Closing balance (credit)		25,000
	1,00,000	1,00,000

Examine what steps would the dealer take, if he is required to maintain a credit balance of Swiss francs 80,000 in the NOSTRO A/c and keep as overbought position on Swiss francs 10,000? [Practice Question]
Answer:
Exchange Position/currency position

Particulars	(Swiss Francs)
Balance in the NOSTRO A/c Credit	1,00,000
Opening position overbought	50,000
Purchased a bill on Zurich	80,000
Sold forward TT	60,000
Forward purchase contract cancelled	30,000
Remitted by TT	75,000
Draft on Zurich cancelled	30,000

The Bank has to buy spot TT Sw. Fcs. 55,000 to increase the balance in Nostro account to Sw. Fcs. 80,000. This would bring down the oversold position on Sw. Fcs. as Nil, rather there will be an overbought position of 50,000. Since the bank requires an overbought position of Sw. Fcs. 10,000, it has to sell forward Sw. Fcs. 40,000

Question 103.
Suppose you are a dealer of ABC Bank and on 20.10.2014 you found that balance in your Nostro account with XYZ Bank in London is £65000 and you had overbought £ 35,000. During the day following transaction have t^ken place:

Particulars	Purchase Sw. Fes	Sale Sw. Fes
Opening Balance Overbought	50,000
Bill on Zurich	80,000
Forward Sales – TT		60,000
Cancellation of Forward Contract		30,000
TT Sales		75,000
Draft on Zurich cancelled	30,000
Closing Balance Oversold	5,000
	1,65,000	1,65,000
Cash Position (Nostro A/c)	Credit	Debit
Opening balance credit	1,00,000
TT sales		75,000
	1,00,000	75,000
Closing balance (credit)		25,000
	1,00,000	1,00,000

What steps would you take, if you are required to maintain a credit Balance of £ 7,500 in the Nostro A/c and keep as overbought position on £7,500?
Answer:
Exchange Position:

	£
DD purchased	12,500
Purchased a Bill on London	40,000
Sold forward TT	30,000
Forward purchase contract cancelled	15,000
Remitted by TT	37,500
Draft on London cancelled	15,000

Cash Position (Nostro A/c)

	Credit £	Debit £
Opening balance credit	65,000	–
TT Remittance	–	37,500
	65,000	37,500
Closing balance (credit)	–	27,500
	65,000	65,000

To maintain Cash Balance in Nostro Account at £7500 you have to sell £20,000 in Spot which will bring Overbought exchange position to Nil. Since bank require Overbought position of £7500 it has to buy the same in forward Market.

Question 104.
The price of a bond just before a year of maturity is $ 5,000. Its redemption Value is $ 5,250 at the end of the said period. Interest is $ 350 p.a. The Dollar appreciates by 2% during the said period. Calculate the rate of return. [May 2012] [5 Marks]
Answer:
Assumption:
(i) If investor is from US then there will be no impact of appreciation in $,
(ii) If investor is from any other nation then there will be impact of $ appreciation on his returns.
First we shall compute return on bond which will be common for both investors.
Return = $\frac{(\text { Price at end }- \text { Price at beginning })+\text { Interest }}{\text { Price at beginning }}$
= $\frac{(5,250-5,000)+350}{5,000}$
= $\frac{250+350}{5,000}$ = 0.12 i.e. 12%
(i) For US investor the return shall be 12% and there will be no impact of appreciation in $.
(ii) If $ appreciate by 2% then return for non-US investor shall be appreciation in interest as well as appreciation in principal due to exchange fluctuation. Hence, his return will be:
(1 + 0.12) (1 + 0.02) – 1 = 1.12 × 1.02 – 1 = 0.1424 i.e. 14.24%

Question 105.
A company is considering hedging its foreign exchange risk. It has made a purchase on 1st January, 2008 for which it has to make a payment of US $ 50,000 on September 30, 2008. The present exchange rate is 1 US $ = $ 40. It can purchase forward 1 US $ at ₹ 39. The company will have to make upfront premium of 2% of the forward amount purchased. The cost of funds to the company is 10% per annum and the rate of Corporate tax is 50%. Ignore taxation. Consider the following situations and compute the Profit/Loss the company will make if it hedges its foreign exchange risk.
(i) If the exchange rate on September 30, 2008 is ₹ 42 per US $.
(ii) If the exchange rate on September 30, 2008 is ₹ 38 per US $. [May 2008] [8 Marks]
Answer:

Particulars	Amt. (₹)
Present Exchange Rate of 1 USD	₹ 40
If company purchases USD 50,000
Forward premium is 50,000 × 39 × 2%	39,000
Interest on ₹ 39,000 for 9 months at 10%	2,925
Total hedging cost	41,925
(i) If exchange rate turns out to be 1 USD	₹ 42
Then gain (₹ 42- 39) for USD 50,000	1,50,000
Less cost of hedging	41,925
Net gain	1,08,075
(ii) If exchange Rate = 1 USD	₹ 38
Then loss (39 – 38) for USD 50,000	50,000
Add: Hedging cost	41,925
Total Loss	91,925

Question 106.
A company is considering hedging its foreign exchange risk. It has made a purchase on 1st July, 2016 for which it has to make a payment of US$ 60,000 on December 31, 2016. The present exchange rate is 1 US $ = ? 65. It can purchase forward 1 $ at ? 64. The company will have to make an upfront premium @ 2% of the forward amount purchased. The cost of funds to the company is 12% per annum.
In the following situations, compute the profit/loss the company will make if it hedges its foreign exchange risk with the exchange rate on 31st December, 2016 as:
(i) ₹ 68 per US $.
(ii) ₹ 62 per US $.
(iii) ₹ 70 per US $.
(iv) ₹ 65 per US $. [Nov. 2016] [8 Marks]
Answer:
1. On 31st December, 2016

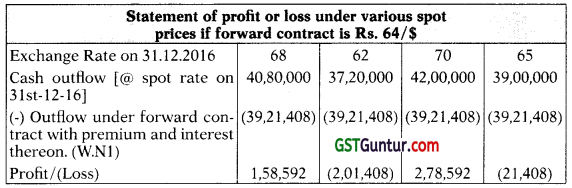
Working Note (IFTV. 1)
Cash flow with Forward contract

Question 107.
ABC Ltd. of UK has exported goods worth Can $ 5,00,000 receivable in 6 months. The exporter wants to hedge the receipt in the forward market. The following information is available:
Spot Exchange Rate 1£ = Can$ 2.5
Interest Rate in UK = 12%
Interest Rate in Canada = 15%
The forward rates truly reflect the interest rates differential. Find out the gain/loss to UK exporter if Can $ spot rates (i) declines 2%, (ii) gains 4% or
(iii) remains unchanged over next 6 months. [May 2016] [8 Marks]
Answer:
According to Interest Rate Parity
Forward rate after 6 months = Spot rate $\left[\frac{1+\text { Interest rate in } \text { Canada }}{1+\text { Interest rate in } U K}\right]^{\prime}$
Forward Rate = $\frac{2.50(1+0.075)}{(1+0.060)}$ = Can$ 2.535/E

(i) If Canadian $ spot rate decline by 2% then the rate will be
$\frac{1}{2.5}$ × 0.98 = $\frac{0.392 £}{\text { Can. } \$}$ = Can $ $\frac{1}{0.392}$/£ = Can$ 2.5510/£

	£
£ receipt as per Forward Rate (Can S 5,00,000/Can $ 2.535)	1,97,239
£ receipt as per Spot Rate (Can $ 5,00,000/Can $ 2.5510)	1,96.002
Gain due to forward contract	1,97,239

(ii) If Canadian $ spot rate gains by 4% then the rate will be
$\frac{1}{2.5}$ × 1.04 = $\frac{0.416 £}{\text { Can. } \$}$ = Can $ $\frac{1}{0.416}$/£ = Can$ 2.4038/£

	£
£ receipt as per Forward Rate (Can $ 5,00,000/Can $ 2.535)	1,97,239
£ receipt as per Spot Rate (Can $ 5,00,000/Can $ 2.4038)	2,08,004
Loss due to forward contract	10,765

(iii) If spot rate remains unchanged

	£
£ receipt as per Forward Rate (Can $ 5,00,000/Can $ 2.535)	1,97,239
£ receipt as per Spot Rate (Can $ 5,00,000/Can $ 2.50)	2,00,000
Loss due to forward contract	2,761

Question 108.
Drill dip Inc. a US Based Company has won a contract in India for drilling oil field. The project will require an initial investment of ₹ 500 crores. The oil field along with equipment will be sold to Indian Government for ₹ 740 crores in one year time. Since the Indian government will pay for the amount in Indian Rupee (₹) the company is worried about exposure due to exchange rate volatility.
Your are required to:
(a) Construct a swap that will help the drill dip to reduce the exchange rate risk.
(b) Assuming that Indian Government offers a swap at spot rate which is 1US$ = ₹ 50 in one year, then should the company opt for this option or should it just do nothing. The spot rate after one year is expected to be 1US$= ₹ 54. Further you may also assume that the Drill dip can also take a US$ loan at 8% p.a. [May 2019 RTP]
Answer:
(a) The following swap arrangement can be entered by Drill dip.
1. Swap a US$ loan today at an agreed rate with any party to obtain Indian Rupees to make initial investment.
2. After one year swap back the Indian Rupees with US$ at the agreed rate. In such case the company is exposed only on the profit earned from the project.

(b) With the swap

	Year 0 (Million US$)	Year 1 (Million US$)
Buy ₹ 500 crores at spot rate of 1 US$ = ₹ 50	(100.00)	………………..
Swap ₹ 500 crores back at agreed rate of ₹ 50	………………….	100.00
Sell ₹ 240 crores at 1US$ = ₹ 54	…………………	44.44
Interest on US$ loan @8% for one year	………………..	(8.00)
	(100.00)	136.44

Net result is a net receipt of US$36.44 million.
Without the swap

	Year 0 (Million US$)	Year 1 (Million US$)
Buy ₹ 500 crore at spot rate of 1US$ = ₹ 50	(100.00)	………………………….
Sell ₹ 740 crore at 1US$ = ₹ 54	…………………………….	137.04
Interest on US$ loan @8% for one year	………………………………	(8.00)
	(100.00)	129.04

Net result is an receipt of US$ 29.04 million
Decision: since the net receipt is higher in swap option the company should opt for the same.

Foreign Exchange Exposure and Risk Management – CA Final SFM Study Material

Leave a Comment Cancel Reply