Differential Calculus – CA Foundation Maths Study Material

This Differential Calculus – CA Foundation Maths Study Material is designed strictly as per the latest syllabus and exam pattern.

Differential Calculus – CA Foundation Maths Study Material

Previous Year Exam Questions

Question 1.
The slope of the tangent at the point (2, -2) to the curve x² + xy + y² – 4 = 0 is given by: [1 Mark, Nov. 2006]
(a) 0
(b) 1
(c) -1
(d) None
Answer:
(b) is correct.
Diff. w.r.t. x; we get

Question 2.
The derivative of x²log x is: [1 Mark, Nov. 2006]
(a) 1 + 2log x
(b) 2 log x
(c) x(1 + 2logx)
(d) None of these
Answer:
\(\frac{d}{d x}\)(x2 log x)
= \(\frac{d x^2}{d x}\)log x + x\(\frac{d \log x}{d x}\)
= 2x log x + x
= x(2 log x + 1)

Question 3.
If x = y log (xy), then \(\frac{d y}{d x}\) is equal to:

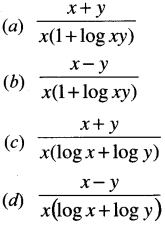
Answer:
(b) is correct
x – y log(xy) = 0

Tricks:

Question 4.
If y = 2x + \(\frac{4}{x}\),then x \(\frac{d^2 y}{d x^2}\) + x\(\frac{dy}{dx}\) – y yields: [1 Mark, Feb. 2007]
(a) 3
(b) 1
(c) 0
(d) 4
Answer:
(c) is correct.

Question 5.
If f(x) = x^k and f’ (1) = 10, then the value of k is: [1 Mark, May 2007]
(a) 10
(b) -10
(c) 1/10
(d) None
Answer:
(a) is correct.
∵ f(x) = x^k
∵ f’(x) k.x^k-1
∵ f(1) = k.(1^k-1) = 10
or k × 1 = k = 10

Question 6.
Given x = 2t + 5; y = t² – 2, then is calculated as: [1 Mark, May 2007]
(a) t
(b) 1/t
(c) -1/t
(d) None
Answer:
(a) is correct
\(\frac{d y}{d x}=\frac{d y / d t}{d x / d t}=\frac{2 t-0}{2+0}=\frac{2 t}{2}\) = t

Question 7.
If x^y = y^x, then \(\frac{d y}{d x}\) gives: [1 Mark, Aug. 2007]

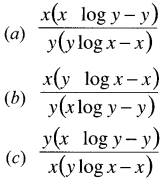
(d) None of these
Answer:
(c) is correct
∵ x^y = y^x
Taking log on both sides; We get
log x^y = log y^x
or y log x = x log y

Differentiating on both sides; We get

Question 8.
If x³ – 2x²y² + 5x + y = 5, then \(\frac{d y}{d x}\) at x = 1 and y = 1 is:
(a) 4/3
(b) -5/4
(c) 4/5
(d) -4/3
Answer:
(a) is correct
∴ x³ – 2x²y² + 5x + y = 5

Differentiating on both sides w.r.t x

Question 9.
If y = (x + \(\sqrt{\mathrm{x}^2+\mathrm{m}^2}\)) then \(\frac{d y}{d x}\) =
(a) \(\frac{n y}{\sqrt{x^2+m^2}}\)
(b) ny
(c) –\(\frac{n y}{\sqrt{x^2+m^2}}\)
(d) None
Answer:
(a) is correct

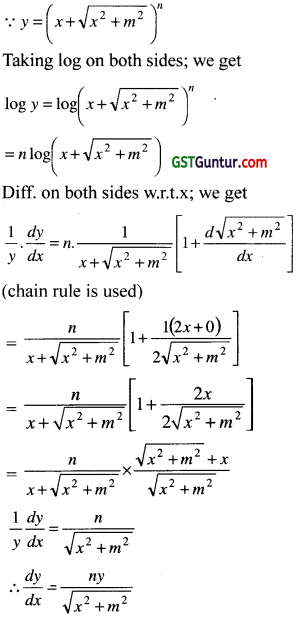
Question 10.
If xy(x – y) = 0, find \(\frac{d y}{d x}\): [1 Mark, Nov. 2007]

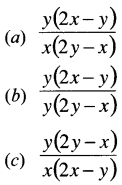
(d) None of these
Answer:
(a) is correct
∵ xy(x – y) = 0
or x²y – xy² = 0

Differentiating on both sides; we get

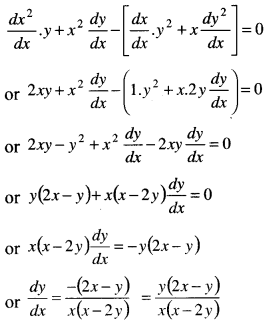
Tricks: Do as Qts no. 3

Question 11.
If y = √x^{√x√x……..to ∞} Then \(\frac{\mathrm{dy}}{\mathrm{dx}}\) is equal to: [1 Mark, Nov. 2007]
(a) \(\frac{y^2}{\log x}\)
(b) \(\frac{y^2}{2-y \log x}\)
(c) \(\frac{y^2}{x(2-y \log x)}\)
(d) None of these
Answer:
(c) is correct

Question 12.
If y = 1 + x + \(\frac{x^2}{2 !}+\frac{x}{3}\) + ………. + \(\frac{x^n}{n}\) ……… then \(\frac{d y}{d x}\) – y is equal to: [1 Mark, Nov. 2007]
(a) 1
(b) – 1
(c) 0
(d) None
Answer:
(c) is correct
∵ y = 1 + x + \(\frac{x^2}{2 !}\) + ……….. to ∞ = e^x
(It is formula)
y = e^x
\(\frac{d y}{d x}=\frac{d e^x}{d x}\) = e^x = y
\(\frac{d y}{d x}\) – y = 0

Question 13.
The slope of the tangent to the curve y = \(\sqrt{4-x^2}\) at the point, where the ordinate and the abscissa are equal, is:
(a) -1
(b) 1
(c) 0
(d) None of these
Answer:
(a) is correct
∵ Ordinate = Abscissa (given)
y = x ………..(i)

Question 14.
Differentiate e^(xx): [1 Mark, June 2008]
(a) (1 + log x)
(b) x^x(1 + log x)
(c) e^xx(1 + log x)x^x
(d) e^xx(1 + log x)
Answer:
(c) is correct.
Let y = e^xx …………..(i)
log y = log e^xx = x^xlog e^e = x^x × 1
log y = x^x …………..(ii)
Again Taking log on both sides; we get
log(log y) = log x^x = x log x
Differentiating on both sides; we get

Question 15.
If x^myⁿ = (x + y)^m+n, then find \(\frac{d y}{d x}\). [1 Mark, June 2008]
(a) \(\frac{x}{y}\)
(b) \(\frac{y}{x}\)
(c) xy
(d) None
Answer:
(b) is correct
∵ x^m.yⁿ = (x + y)^m+n
Taking log both sides; we get
m log x + n log y = (m + n)log(x + y)

Differentiating on both sides; we get

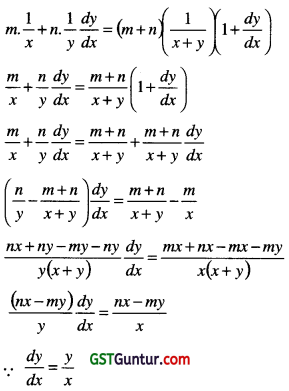
Question 16.
If f(x) = a^xx^a then find f(x), [1 Mark, Dec. 2008]
(a) f(x)[a + log a]
(b) f(x)[\(\frac{a}{x}\) – log a]
(c) f(x)[\(\frac{a}{x}\) – log a]
(d) f(x)[a + xlog a]
Answer:
(a) is correct
∵ f(x) = a^xx^a
f'(x) = \(\frac{d a^x}{d x}\).x + a \(\frac{d x^a}{d x}\)
= a^x.log_e a.x^a + a^x.a.x^a-1
= a^x.x^a. log a + a^x.x^a-1.\(\frac{x}{x}\).a
= a^x.x^a.log a + a^x.x^a.\(\frac{a}{x}\)
= a^x.x^a(log a + \(\frac{a}{x}\))
= f(x)(\(\frac{a}{x}\) + log a)

Question 17.
If x³y² = (x – y)⁵. Find \(\frac{d y}{d x}\) at (1, 2). [1 Mark, June 2009]
(a) -7/9
(b) 7/9
(c) 9/7
(d) -9/7
Answer:
(a) is correct
∵ x²y² = (x – y)⁵
Differentiating on both side;

Question 18.
x = 2t + 5 and y = t² – 5, then \(\frac{d y}{d x}\) =? [1 Mark, Dec. 2009]
(a) t
(b) -1/t
(c) 1/t
(d) 0
Answer:
(a) is correct

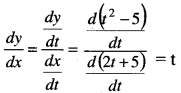
Question 19.
x = at²; y = 2at, \(\frac{d y}{d x}\) = ? [1 Mark, Dec. 2009]
(a) 1/t
(b) – 1/t
(c) t
(d) None of the above
Answer:
(a) is correct
\(\frac{d y}{d x}=\frac{d y / d t}{d x / d t}=\frac{\frac{d(2 a t)}{d t}}{\frac{d\left(a t^2\right)}{d t}}=\frac{2 a \times 1}{a .2 t}=\frac{1}{t}\)

Question 20.
Find the second derivative of y = \(\sqrt{x+1}\). [1 Mark, Dec. 2009]
(a) 1/2(x + 1)^-1/2
(b) -1/4(x + 1)^-3/2
(c) 1/4(x + 1)^-1/2
(d) None of these
Answer:
(b) is correct

Question 21.
If x² + y² = 4 then. [1 Mark, Dec. 2008]

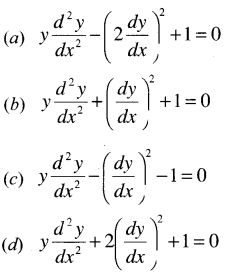
Answer:
(b) is correct,
∵ x² + y² = 4
Differentiating on both side w.r.t x ; we get
2x + 2y \(\frac{d y}{d x}\) = 0
Again diff. on both side ; we get
2×1 + 2\(\frac{d y}{d x}\left(\frac{d y}{d x}\right)\) + 2y\(\frac{d^2 y}{d x^2}\) = 0
1 + \(\left(\frac{d y}{d x}\right)^2\) + y\(\frac{d^2 y}{d x^2}\) = 0

Question 22.
The cost function for the production of x units of a commodity is given by
∵ C(x) = 2x³ – 15x² + 36x + 15
The cost will we minimum when ‘x’ equal to: [1 Mark, Dec. 2010]
(a) 3
(b) 2
(c) 1
(d) 4
Answer:
(a) is correct.
∵ C(x) = 2x³ -15x² + 36x + 15
Diff. on both side w.r.t. x; we get
C’ (X) = 6X² – 30X + 36
C”(X) = 12X – 30
For maxima or minima
C'(X) = 0
∴ 6X² – 30X + 36 = 0
X² – 5X + 6 = 0
X² – 3X – 2X + 6 = 0
X(X – 3) – 2(X – 3) = 0
(X – 3)(X – 2) = 0
so; x = 3; x = 2
Now C”(X = 3) = 12x³ – 30 = 6 >0
So; C (X) is minimum at x = 3

Question 23.
If f(x) = ^XC₃; then f'(1) = ?
(a) \(\frac{1}{6}\)
(b) \(\frac{-1}{6}\)
(c) \(\frac{5}{6}\)
(d) \(\frac{-5}{6}\)
Answer:
(b) is correct.

Question 24.
\(\frac{\mathrm{d}}{\mathrm{dx}}\)[2^log₂x] = ____. [1 Mark, Dec. 2011]
(a) 1
(b) 0
(c) 1/2
(d) 2^x.log₂x
Answer:
(a) is correct.
\(\frac{\mathrm{d}}{\mathrm{dx}}\)2^log₂x = \(\frac{\mathrm{d}(\mathrm{x})}{\mathrm{dx}}\) = 1
Formula (∵ alog₂x = x)

Question 25.
If Y = X^x then \(\frac{d^2 y}{d x^2}\) = ____. [1 Mark, Dec. 2011]
(a) \(\frac{d Y}{d x}\) (1 + log x)+ Y \(\frac{d}{d x}\) (1 + log x)
(b) \(\frac{d Y}{d x}\) (1 + log x)+ \(\frac{d}{d x}\) (1 + log x)
(c) \(\frac{d Y}{d x}\) (1 + log x)- Y\(\frac{d}{d x}\)(1 + log x)
(d) \(\frac{d Y}{d x}\) (1 + log x) – \(\frac{d}{d x}\)(1 + log x)
Answer:
(a) is correct.
If y= X^x
taking log on both side
log y = log x^x
log y = x log x
Diff w.r.t (x)

Question 26.
If x = c t, y = c/t, then \(\frac{dy}{d x}\) is equal to : [1 Mark, June 2012]
(a) 1/t
(b) t.e^t
(c) -1/t²
(d) None of these
Answer:
(c) is correct

Question 27.
If y = e^alogx + e^xloga, then \(\frac{d y}{d x}\) = [1 Mark, June 2012]
(a) X^a + a^x
(b) a.X^a-1 + a^xlog a
(c) aX^a-1 + Xa^x-1
(d) X^x + a^a
Answer:
(b) is correct.
y = e^alogx + e^xloga
⇒ y = x^a + a^x
[∵ e^{log m} = m]
DifF. w.r.t. x on both side ; we get
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = ax^a-1 + a^x log a

Question 28.
For the function y = x³ – 3x, the value of \(\) at which \(\) is zero, is: [1 Mark, Dec 2012]
(a) ±1
(b) ±3
(c) ±6
(d) None of these
Answer:
(c) is correct
Given y = x³ – 3x
DifF. w.r.t. ‘x’
\(\frac{d y}{d x}\) = 3x² – 3 ………….(1)
0 = 3(x² – 1)
x² – 1 = 0
x² = 1;
so x = ±1
DifF. (1) w.r.t ‘x’
\(\frac{d^2 y}{d x^2}=\frac{d}{d x}\)(3x² – 3) = 6x
\(\left(\frac{d^2 y}{d x^2}\right)_{(x=\pm 1)}\) = 6(±1) = ±6

Question 29.
The equation of the tangent to the curve, x³ – 2x + 3, at the point (2, 7) is: [1 Mark, Dec. 2012]
(a) y = 2x – 13
(b) y = 10x
(c) y = 10x – 13
(d) y = 10
Answer:
(c) is correct. Given that
f(x) = x² – 2x + 3
i.e.y = x² – 2x + 3
\(\frac{d y}{d x}\) = 3x² – 2
\(\left(\frac{d y}{d x}\right)_{(2,7)}\) = 3(2)² – 2
= 12 – 2
\(\left(\frac{d y}{d x}\right)_{(2,7)}\) = 10
Slope of tangent m = \(\left(\frac{d y}{d x}\right)_{(2,7)}\) = 10
The equation of tangent at (2, 7)
y – y₁ = m(x – x₁)
y – 7 = 10(x – 2)
y – 7 = 10x – 20
y = 10x – 20 + 7
y = 10x – 13
Tricks : GBC

Question 30.
If y = y log\(\left[\frac{5-4 x^2}{3+5 x^2}\right]\), then \(\frac{d y}{d x}\) = ____. [1 Mark, Dec. 2012]
(a) \(\frac{8}{4 x-5}-\frac{10}{3+5 x}\)
(b) (4x² – 5) – (3 + 5x²)
(c) \(\frac{8 x}{4 x^2-5}-\frac{10 x}{3+5 x^2}\)
(d) 8x – 10
Answer:
(c) is correct
Since, y = log\(\left(\frac{5-4 x^2}{3+5 x^2}\right)\)
y = log(5 – 4x²) – log(3 + 5x²)
Diff. wrt x

Question 31.
If y = log_yx then \(\frac{d y}{d x}\) = [1 Mark, June 2013]
(a) \(\frac{1}{x \log y}\)
(b) \(\frac{1}{x+x \log y}\)
(c) \(\frac{1}{1+x \log y}\)
(d) \(\frac{1}{y+\log x}\)
Answer:

Question 32.
y = e^t & x = logt; then \(\frac{d y}{d x}\) = [1 Mark, June 2013]
(a) \(\frac{1}{t}\)
(b) te^t
(c) \(-\frac{t}{t^2}\)
(d) None
Answer:
(b) \(\frac{d y}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}}=\frac{e^t}{\frac{1}{t}}\) = te^t
(b) is correct.

Question 33.
The points on the curve y = x³ -x² -x + 1. Where the tangent is parallel to x- axis are: [1 Mark, Dec. 2013]
(a) (1, 0)\(\left(\frac{-1}{3}, \frac{32}{27}\right)\)
(b) (1,0) (1,1)
(c) \(\left(\frac{-1}{3}, \frac{21}{37}\right)\)(0, 0)
(d) (0,0) (1,0)
Answer:
(a) is correct,
∵ y = x³ – x² – x + 1
\(\frac{d y}{d x}\) = 3x² – 2x – 1
∵ Tangent is parallel to x – axis
\(\frac{d y}{d x}\) = 0
3x² – 2x – 1 = 0
or 3x² – 3x + x – 1 = 0
or 3x(x – 1) + 1 (x – 1) = 0
or (x – 1) (3x + 1) = 0
∴ x = 1; x = -1/3
At x = 1
y = 1³ – 1² – 1 + 1 = 0
∴ Point is (1; 0) and At x = -1/3

Question 34.
A seller makes an offer of selling certain articles that can be described by the equation x = 25 – 2y where x is price per unit and y denotes the No. of units. The cost price of the article is ₹ 10 per unit. The maximum quantity that can be offered in single deal to avoid loss is: [1 Mark, Dec. 2013]
(a) 6
(b) 7
(c) 8
(d) 9
Answer:
(b) is correct,
∵ x = 25 – 2y
Total cost = Cost price per unit x No. of unit sold = 10y
Total sale = Selling price per unit xNo. of units sold
= x.y = (25 – 2y)y = 25y – 2yz
Profit = sale – Cost
= 25y – 2y² – 10y = 15y – 2y²
For No loss; Profit > 0
15y – 2y² >0
or 15 – 2y > 0
or \(\frac{15}{2}\) > y ⇒ y < 7.5
y = No. of units (a whole No.)
∴ y = 7
∴ Maximum Quantity sold y = 7
Tricks : Go by choices

Question 35.
If y = a.e^nx + b.e^-nx then \(\frac{d^2 y}{d x^2}\). [1 Mark, June 2014]
(a) n²y
(b) -n²y
(c) ny
(d) None
Answer:
(a) is correct,
y = ae^nx + be^-nx
So; \(\frac{d y}{d x}\) = a.e^nx .n + b.e^-nx (-n)
= n[ae^nx – be^-nx]
\(\frac{d^2 y}{d x^2}\) = n[a.e^nx .n – b.e^-nx (-n)]
= n.n|ae^nx + be^-nx]
= n².y

Question 36.
If y = 1 + \(\frac{x}{1 !}+\frac{x^2}{2 !}\) + ……… + \(\frac{x^n}{n !}\) + …………., then the value of \(\frac{d y}{d x}\) – y = ____
(a) 1
(b) 0
(c) -1
(d) None
Answer:
(b) is correct.

Question 37.
If e^xy – 4xy = 4 then \(\frac{d y}{d x}\) = ____. [1 Mark, June 2015]
(a) \(\frac{y}{x}\)
(b) \(\frac{-y}{x}\)
(c) \(\frac{x}{y}\)
(d) \(\frac{-x}{y}\)
Answer:
If e^xy – 4xy – 4 = 0

Question 38.
If x^p,y^q = (x + y)^p+q then \(\frac{d y}{d x}\) = . [1 Mark, June 2015]
(a) \(\frac{y}{x}\)
(b) \(\frac{-y}{x}\)
(c) \(\frac{p}{q}\)
(d) \(\frac{-p}{q}\)
Answer:
x^p,y^q = (x + y)^p+q
Tricks \(\frac{d y}{d x}=\frac{y}{x}\)
(a) is correct (see Quicker BMLRS)

Question 39.
Find slope of tangent of curve y = x + 2 at x = 2. [1 Mark, Dec. 2015]
(a) 3/16
(b) 5/17
(c) 9/11
(d) None of the above
Answer:

Question 40.
u = 5t⁴ + 4t⁴ + 2t⁴ + 4 at t = -1 find du/dt. [1 Mark, Dec. 2015]
(a) -11
(b) 11
(c) -16
(d) 16
Answer:
(a) is correct. u = 5t⁴ + 4t³ + 2t² + t + 4
\(\frac{d u}{d t}\) = 5 × 4t⁴ + 4 × 3t³ + 2 × 2t² + t + 4
= 20t³ + 12t⁴ + 4t + 1
\(\frac{d u}{d t}\)at = -1
= 20(-1)³ + 12(-1)² + 4(-1) +1
= -20 + 12 – 4 + 1 = -11

Question 41.
\(\sqrt{\frac{1-x}{1+x}}\) then \(\frac{d y}{d x}\) is equal to ____ . [1 Mark, June 2016]
(a) \(\frac{y}{x^2-1}\)
(b) \(\frac{y}{1-x^2}\)
(c) \(\frac{y}{1+x^2}\)
(d) \(\frac{y}{y^2-1}\)
Answer:
(a) is correct.

Question 42.
\(\frac{d}{d x}\)(log\(\sqrt{x-1}+\sqrt{x+1}\))) = [1 Mark, Dec. 2016]
(a) \(\frac{1}{2 \sqrt{x^2-1}}\)
(b) \(\frac{1}{2 \sqrt{x^2+1}}\)
(c) \(\frac{1}{\sqrt{x-1}+\sqrt{x+1}}\)
(d) None of these
Answer:
(a) is correct.

Question 43.
f(x) = log_e\(\left(\frac{x-1}{x+1}\right)\) and f'(x) = 1 then the value of x =
(a) 1
(b) 0
(c) ±√3
(d) ±√2
Answer:
(c) is correct
Soln.
f(x) = log_e\(\left(\frac{x-1}{x+1}\right)\) = log_e(x – 1) – log_e(x + 1)

⇒ x² – 1 = 2
⇒ x² = 3
x = ±√3

Question 44.
The equation of the curve which passes through the point (1,2) and has the slope 3x – 4 at any point (x, y) is: [1 Mark, June 2017]
(a) 2y = 3x² – 8x + 9
(b) y = 6x² – 8x + 9
(c) y = x² – 8x + 9
(d) 2y = 3x² – 8x + c
Answer:
Tricks: Go by choices for option (a) point (1,2) satisfies
2y = 3x² – 8x + 9 and its slope is
2.\(\frac{d x}{d x}\) = 3 × 2x – 8 × 1 + 0
6x – 8 = 2(3x – 4)
\(\frac{d x}{d x}\) = slope = 3x – 4 (True)
Option (a) is correct.

Question 45.
If y = 1 + \(\frac{x^1}{1 !}+\frac{x^2}{2 !}+\frac{x^3}{3 !}\) + ………………… then \(\frac{d y}{d x}\) = ____: [1 Mark, Dec. 2017]
(a) x
(b) y
(c) 1
(d) 0
Answer:
y = 1 + \(\frac{x^1}{1 !}+\frac{x^2}{2 !}+\frac{x^3}{3 !}\) + ……….
⇒ y = e^x (Formula)
\(\frac{d y}{d x}=\frac{d e^x}{d x}\) = e^x = y
\(\frac{d y}{d x}\) = y
(b) is correct.

Question 46.
If x = a.t² and y = 2at then \(\left(\frac{d y}{d x}\right)_{t=2}\) = ____ [1 Mark, Dec. 2017]
(a) 2
(b) 4
(c) 1/2
(d) 1/4
Answer:
(c) is correct

Question 47.
If x^y = e^x-y then \(\frac{d y}{d x}\) = ____ : [1 Mark, Dec. 2017]
(a) \(\frac{2 \log x}{(1+\log x)^2}\)
(b) \(\frac{\log x}{1+\log x}\)
(c) \(\frac{\log x}{(1+\log x)^2}\)
(d) None of these
Answer:
(c)
∵ x^y = e^x-y
Taking log on both sides ; we get
ylogx = (x – y).loge = x – y
or; y + .ylogx = x
or; y (1 + logx) = x

Question 48.
If y = log x^x then \(\frac{d y}{d x}\) = ____ : [1 Mark, Dec. 2017]
(a) log (ex)
(b) log(e/x)
(c) log(x/e)
(d) 1
Answer:
(a)
y = log x^x = xlogx
\(\frac{d y}{d x}\) = 1. log x + x × \(\frac{1}{x}\)
= 1 + log x
= log_ee + log_ex
= log_e (ex)
= log (ex)

Question 49.
The cost function for the production of x units of a commodity is given by C(x) = 2x³ – 15x² + 36x + 15 The cost will be minimum when x = ? [1 Mark, May 2018]
(a) 3
(b) 2
(c) 1
(d) 4
Answer:
(a)
Let
∵ C(x) = y = 2x³ – 15x² + 36x + 15
\(\frac{d y}{d x}\) = 6x² – 30x + 36
\(\frac{d^2 y}{d x^2}\) = 12x – 30
If \(\frac{d y}{d x}\) = 0 ⇒ 6x² – 30x + 36 = 0
or 6(x² – 5x + 6)=0
or 5x² – 3x – 2x + 6 = 0
or ; x (x – 3)- 2(x – 3)= 0
or (x – 2)(x – 3) = 0
x = 2;3.

Case – I:
\(\frac{d^2 y}{d x^2}\) at x = 2 = 12 × 2 – 30 = -6 < 0. ∴ c(x) is maximum at x = 2. Case-II: \(\frac{d^2 y}{d x^2}\) at x = 3 = 12 × 3 – 30 = 6 > 0.
∴ y = c(x) is minimum at x = 3.
∴ (a) is correct.

Question 50.
Let x = at, y = \(\frac{a}{t^2}\), Then \(\frac{d y}{d x}\). [1 Mark, Nov. 2018]
(a) \(\frac{-3 a}{t^6}\)
(b) \(\frac{-1}{t^6}\)
(c) \(\frac{1}{3 a t^2}\)
(d) None
Answer:
(d)

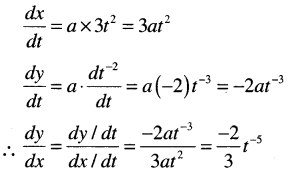
Question 51.
xy = 1 then y² + \(\frac{d y}{d x}\) = ? [1 Mark, Nov. 2018]
(a) 1
(b) 0
(c) 2
(d) None
Answer:
(b)

Question 52.
If the given cost function of commodity is given by C = 150x – 5x² + \(\frac{x^3}{6}\), where C stands for cost and x stands for output, if the average cost is equal to the marginal cost then the output x = ____. [1 Mark, June 2019]
(a) 5
(b) 10
(c) 15
(d) 20
Answer:

or x = 0; \(\frac{x}{3}\) – 5 = 0
or \(\frac{x}{3}\) = 5
∴ x =15
∴ (c) is correct.

Question 53.
If 2^x – 2^y = 2^x-y then at x = y = 2. [1 Mark, June 2019]
(a) 1
(b) 2
(c) 4
(d) 5
Answer:
(a)
Given 2^x – 2^y = 2^x-y = 0
Tricks: It is implicit function
So,

(a) is correct.