Correlation – CA Foundation Statistics Solutions

These Correlation –  CA Foundation Statistics Notes are designed strictly as per the latest syllabus and exam pattern.

Correlation – CA Foundation Statistics Notes

Previous Year Exam Questions

Question 1.
The coefficient of correlation r between x and y when: Cov. (x, y) = -16.5, Var (x) = 2.89, Var (y) = 100 is: [1 Mark, Nov. 2006]
(a) -0.97
(b) 0.97
(c) 0.89
(d) -0.89
Solution:
(a)
Coefficient of correlation
r = \(\frac{\text{cov}(x, y)}{\sigma_x \cdot \sigma_y}\) = \(\frac{-16.5}{\sqrt{2.89} \times \sqrt{100}}\) = \(\frac{-16.5}{1.7 \times 10}\)
= – 0.97

Question 2.
Take 200 and 150 respectively as the assumed mean for X and Y series of 11 values, then dx = X- 200, dy = Y – 150, Σ dx = 13, Σ dx² = 2667, Σ dy = 42, Σ dy² = 6964, Σ dx dy = 3943. The value of r is: [1 Mark, Nov. 2006]
(a) 0.77
(b) 0.98
(c) 0.92
(d) 0.82
Solution :
(c) Formula
r = \(\frac{n \sum d x d y-\sum d x \cdot \sum d y}{\sqrt{n \sum d^2-\left(\sum d x\right)^2} \sqrt{n \sum d y^2-\left(\sum d y\right)^2}}\)
r = \(\frac{11 \times 3943-13 \times 42}{\sqrt{11 \times 2667-(13)^2} \sqrt{11 \times 6964-(42)^2}}\)
= 0.92

Question 3.
If the sum of squares of the rank difference in Mathematics and Physics marks of 10 students is 22, then the coefficient of rank correlation is:  [1 Mark Feb. 2007]
(a) 0.267
(b) 0.867
(c) 0.92
(d) None
Solution:
(b) Coefficient of Rank Correlation
R = 1 – \(\frac{6 \sum d^2}{n\left(n^2-1\right)}\) = 1 – \(\frac{6 \times 22}{10\left(10^2-1\right)}\)
= 1 – \(\frac{6 \times 2}{10 \times 9}\) = \(\frac{13}{15}\) = 0.867(approx)

Question 4.
The coefficient of correlation between X and Y is 0.6. U and V are two variables defined as U = \(\frac{x-3}{2}\), V = \(\frac{y-2}{3}\), then the coefficient of correlation between U and V is : [1 Mark, May 2007]
(a) 0.6
(b) 0.4
(c) 0.8
(d) 1
Solution:
(a) Since correlation coefficient (Karl Pearson’s) is independent of the change of scale and origin,
So ; r(u, v) = r(x, y) = 0.6 [Because X & Y have same sign]
Tricks : See Quicker BMLRS CORRELATION

Question 5.
For the following data, the coefficient of rank correlation is : [1 Mark, May 2007]

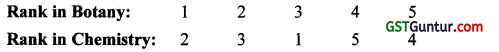
(a) 0.93
(b) 0.4
(c) 0.6
(d) None
Solution:
(c)

Where R1 = Rank in Botany
R₂ = Rank in Chemistry
Hence coefficient of rank correlation
R = 1 – \(\frac{6 \times 8}{5\left(5^2-1\right)}\) = 1 – \(\frac{2}{5}\) = 0.6

Question 6.
For 10 pairs of observations, number of concurrent deviations was found to be 4. What is the value of the coefficient of concurrent deviation? [1 Mark, Aug. 2007]
(a) \(\sqrt{0.2}\)
(b) 1/3
(c) -1/3
(d) –\(\sqrt{0.2}\)
Solution:
(c)
Given C = 4, N = 10,
So, n = N – 1 = 10 – 1 = 9
2C – n = 2.4 – 9 = -1 (-ve)
∵ r_c = ± \(\sqrt{\frac{\pm(2 c-n)}{n}}\)
∴ r_c = –\(\sqrt{\frac{-(2 \times 4-9)}{9}}\) ⇒ r_c = \(\frac{(-1)}{3}\) = –\(\frac{1}{3}\)
Note : Here (2c – n) = – ve, so – ve sign taken at both the places.

Question 7.
In rank correlation, the association need not be linear: [1 Mark, Nov. 2007]
(a) True
(b) False
(c) Partly True
(d) Partly False
Solution:
(a)
In Spearman’s Rank Correlation; the association need not be Linear because it is based on ranks of observations not on actual observations.

Question 8.
The coefficient of rank correlation of marks obtained by 10 students, in English and Economics was found to be 0.5. It was later discovered that the difference in ranks in the two subjects obtained by one student was wrongly taken as 3 instead of 7. The correct coefficient of rank correlation is : [1 Mark, Feb. 2008]
(a) 0.32
(b) 0.26
(c) 0.49
(d) 0.93
Solution:
(b) Given Incorrect R = 0.5 ; N = 10 ; Incorrect D = 3, Correct D = 7
Coefficient of rank correlation = R = \(\frac{6 \sum D^2}{\mathrm{~N}\left(\mathrm{~N}^2-1\right)}\)
⇒ 0.5 = 1 – \(\frac{6 \sum D^2}{10\left(10^2-1\right)}\) ⇒ \(\frac{6 \sum D^2}{990}\) = 0.5
⇒ ΣD² = 82.5 [Incorrect because incorrect R = 0.5 is used here]
Corrected value of ΣD² = 82.5 – 3² + 7² = 122.5
Corrected R = 1 – \(\frac{6 \times 122.5}{990}\) = 1 – \(\frac{735}{990}\) = 1 – 0.74 = 0.26

Question 9.
The coefficient of correlation between x and y series from the following data: [1 Mark, June 2008]

Sum of the product of the deviations of X and Y series from their respective means = 122, is :
(a) 0.89
(b) 0.99
(c) 0.69
(d) 0.91
Solution:
(a) Given ; σ_x = 3.01, σ_y = 3.03, Σ x² = 136
Σ y² =138, Σ xy = 122
Where x = X – \(\overline{\mathrm{X}}\); y = Y – \(\overline{\mathrm{Y}}\)
Formula;
r = \(\frac{\sum x y}{\sqrt{\sum x^2 \times \sum y^2}}=\frac{122}{\sqrt{136 \times 138}}\) = 0.89

Question 10.
If the sum of square of differences of rank is 50 and number of items is 8 then what is the value of rank correlation coefficient. [1 Mark, Dec. 2008]
(a) 0.59
(b) 0.40
(c) 0.36
(d) 0.63
Solution:
(b) Given That ΣD² = 50, N = 8
R = 1 – \(\frac{6 \sum D^2}{N\left(N^2-1\right)}\) = 1 – \(\frac{6 \times 50}{8\left(8^2-1\right)}\) = 1 – \(\frac{6 \times 50}{8 \times 63}\) = 0.40

Question 11.
If coefficient of correlation between x and y is 0.46. Find coefficient of correlation between x and \(\frac{\mathrm{y}}{2}\) [1 Mark, Dec. 2008]
(a) 0.46
(b) 0.92
(c) -0.46
(d) -0.92
Solution:
(a) r_xy = 0.46
RULE: – The value of r does not change with respect to the change of origin and scale.
TRICKS : Sign of r will not change because signs of X & Y are same.

Question 12.
The coefficient of correlation is significant if: [1 Mark, Dec. 2008]
(a) r > 5 P . E
(b) r < 6 P . E
(c) r ≥ 6 × P.E.,
(d) r = 6 P . E
Solution:
(c)
If r ≥ 6 × P.E., then coefficient of correlation is significant and the correlation exists.

Question 13.
If Ranks of two characteristics by two judges are in reverse order then find the value of Spearman rank correlation co-efficient. [1 Mark, June 2009]
(a) -1
(b) 0
(c) 1
(d) 0.75
Solution:
(a)
Clearly ; In this case, it is perfectly negatively correlated.
So, r = -1

Question 14.
If the rank correlation co-efficient between marks in Management and Mathematics for a group of students is 0.6 and the sum ofthe squares ofthe difference in rank is 66. Then what is the number of students in the group ? [1 Mark, Dec. 2009]
(a) 9
(b) 10
(c) 11
(d) 12
Solution:
(b) Given, R = 0.6 ; Σ D² = 66
R = 1 – \(\frac{6 \sum D^2}{N\left(N^2-1\right)}\)
TRICKS : Go by choices,
[See QUICKER BMLRS Tricks ]
Use, directly by calculator
For, N = 10, R = 1 – \(\frac{6 \times 66}{990}\) = 0.6 = Given Value
So, N = 10 is correct.

Question 15.
Correlation coefficient between X and Y will be negative when:- [1 Mark, Dec. 2009]
(a) X and Y are decreasing
(b) X is increasing, Y is decreasing
(c) X and Y are increasing
(d) None of these
Solution:
(b) r is -ve, means X & Y are in reverse order.

Question 16.
If ‘ρ’ is the simple correlation coefficient, the quantity ρ² is known as : [1 Mark, June 2010]
(a) Coefficient of determination
(b) Coefficient of Non-determination
(c) Coefficient of alienation
(d) None of the above.
Solution:
(a)

Question 17.
If the correlation coefficient between X and Y is r, & U = \(\frac{\mathrm{X}-5}{10}\) and V = \(\frac{\mathrm{Y}-7}{2}\) then r_uv is [1 Mark, June 2010]
(a) r
(b) -r
(c) (r-5)/2
(d) (r-7)/10
Solution:
(a) U = \(\frac{\mathrm{X}-5}{10}\) = \(\frac{\mathrm{X}}{10}\) – \(\frac{5}{10}\) & V = \(\frac{\mathrm{Y}}{2}\) – \(\frac{7}{2}\)
TRICKS : Since X & Y have same sign.
So, r_xy = r_uv = r

Question 18.
If the sum of the product of deviations of x and y series from their mean is zero, then the coefficient of correlation will be [1 Mark, Dec, 2010]
(a) 1
(b) -1
(c) 0
(d) None of these
Solution:
(c)
Given \(\sum(\mathrm{X}-\overline{\mathrm{X}})(\mathrm{Y}-\overline{\mathrm{Y}})\) =
Formula, r = \(\frac{\sum(\mathrm{X}-\overline{\mathrm{X}})(\mathrm{Y}-\overline{\mathrm{Y}})}{\mathrm{N} \times \sigma_{\mathrm{x}} \times \sigma_{\mathrm{y}}}\)
= \(\frac{0}{N \times \sigma_x \times \sigma_y}\) = 0

Question 19.
The ranks of five participants given by two judges are [1 Mark, Dec. 2010]

Rank correlation coefficient between ranks will be
(a) 1
(b) 0
(c) -1
(d) 1/2
Solution:
(c) Ranks given by two Judges are in reverse order in same ratio.
∴ R = -1 [It is always -1; No need to proof.]

Question 20.
The covariance between two variables X and Y is 8.4 and their variances are 25 and 36 respectively. Calculate Karl Pearson’s coefficient of correlation between them. [1 Mark, June 2011]
(a) 0.82
(b) 0.28
(c) 0.01
(d) 0.09
Solution:
(b) Given : Cov. (x, y) = 8.4 σ_x = \(\sqrt{25}\) = 5, σ_y = \(\sqrt{36}\) =
r = \(\frac{\text{Cov} .(\mathrm{x}, \mathrm{y})}{\sigma_{\mathrm{x}}, \sigma_{\mathrm{y}}}\) = \(\frac{8.4}{5 \times 6}\) = 0.28

Question 21.
In Spearman’s Correlation Coefficient, the sum of the differences of ranks between two variables shall be [1 Mark, Dec. 2012]
(a) 0
(b) 1
(c) -1
(d) None of them
Solution:
(a) In Spearman’s correlation coefficient the sum of the differences of ranks between two variable shall be Zero.
Σ D = Σ (R₁ – R₂) = 0

Question 22.
The coefficient of correlation between X and Y series is – 0.38 The linear relation between U & Y are 3X + 5U = 3 and -8Y – 7V = 44, what is the coefficient of correlation between U & V? [1 Mark, Dec. 2012]
(a) 0.38
(b) -0.38
(c) 0.40
(d) None of them
Solution:
(b) Given r_xy = – 0.38
TRICKS : 3X + 5U = 3 and
-8Y – 7V = 44
8Y + 7V = 44
r = – 0.38
For Tricks
Note See QUICKER BMLRS Examples

Question 23.
Two variables X and Y are related as 4x + 3y = 7 then correlation between x and y is ___________ [1 Mark, June 2013]
(a) Perfect positive
(b) Perfect negative
(c) Zero
(d) None of these
Solution:
(b)
Since, 4x+3y = 7
∴ 3y = -4x + 7; .∴ r = -1
∴ X and are y perfectly negative because x and y have opposite sign.

Question 24.
If r is the karl pearson’s coefficient of correlation in a bivariate distribution the two regression lines are at right angles when __________ [1 Mark, June 2013]
(a) r = ±1
(b) r = 0
(c) r = ±∞
(d) None
Solution:
(b) If r = 0 ; Two Regression Lines are perpendicular to each other.

Question 25.
If r = 0.28, Cov. (x, y) = 7.6, V(x) = 9 then σ_y = ______________ [1 Mark, June 2013]
(a) 8.75
(b) 9.04
(c) 6.25
(d) None
Solution:
(b) is correct
r = \(\frac{\text{Cov} \cdot(x ; y)}{\sigma_x \cdot \sigma_y}\)
or; 0.28 = \(\frac{7.6}{3 . \sigma_y}\) or σ_y = 9.04

Question 26.
Price and Demand is example for:
(a) No correlation
(b) Positive correlation
(c) Negative correlation
(d) None of these
Solution:
(c)

Question 27.
Determine the coefficient of correlation between x and y series [1 Mark, Dec. 2013]

Sum of product deviation of X and Y series from mean = 122
(a) -0.89
(b) 0.89
(c) 0.69
(d) -0.69
Solution:
(b) is correct

= 0.89
Tricks : Use calculator (Without writing)

Question 28.
When each individual gets the exactly opposite rank by the two judges then the rank correlation will be ____________ [1 Mark, June 2014]
(a) -1
(b) 0
(c) +1
(d) +1/2
Solution:
(a) is correct
Note Opposite Ranks Means r = -1

Question 29.
Correlation coefficient between x and y is 1, then correlation coefficient between x – 2 and (-y/2)+1 is. [1 Mark, Dec. 2014]
(a) 1
(b) -1
(c) -1/2
(d) 1/2
Solution:
(b) is correct,
∵ r = + 1 (given)
For variables (x – 2) and \(\left(-\frac{y}{2}+1\right)\)
r = -1 (because sign of x & y are opposite)

Question 30.
When r = 1, all the points in a scatter diagram would lie: [1 Mark, June 2015]
(a) On a straight line directed from lower left to upper right
(b) On a straight line
(c) On a straight line directed from upper left to lower right
(d) Both (a) and (b)
Solution:
(a) is correct.

Question 31.
In case ‘Insurance Companies’ Profits and the No. of claims they have to pay: [1 Mark, Dec. 2015]
(a) Positive correlation
(b) Negative correlation
(c) No correlation
(d) None of these
Solution:
(b) is correct.

Question 32.
If r = 0.6 then the coefficient of non-determination is __________ [1 Mark, June 2016]
(a) 0.4
(b) -0.6
(c) 0.36
(d) 0.64
Solution:
(d)
co-efficient of Non-determination
= 1 – r² = 1 – (0.6)²
= 0.64
= 64%

Question 33.
If the coefficient of correlation between x and y variables is -0.90 then what will be the coefficient of determination [1 Mark, June 2016]
(a) 0.10
(b) 0.81
(c) 0.94
(d) None
Solution:
(b)
co-eff. of determination = r²
= (-0.90)² = 0.81

Question 34.
If the sum of the squares of Rank differences in the marks of 10 students in two students is 44, then the coefficient of rank correlation is ____________ [1 Mark, Dec. 2016]
(a) 0.78
(b) 0.73
(c) 0.87
(d) None
Solution:
(b) is correct.
Given, N = 10 & Σ D² = 44
R = 1 – \(\frac{6 \sum D^2}{N^3-N}\) = 1 – \(\frac{6 \times 44}{10^3-10}\) = 0.73

Question 35.
Correlation between temperature and power consumption is [1 Mark, June 2017]
(a) Positive
(b) Negative
(c) Zero
(d) None
Solution:
(a)

Question 36.
Coefficient of correlation between X & Y is 0.6. If both X and Y are multiplied by -1. Then resultant coefficient of correlation is [1 Mark, June 2017]
(a) 0.6
(b) Negative
(c) 1/0.6
(d) None
Solution:
(a) [∵ r does not change with respect to the change of origin and scale]

Question 37.
If r = 0.6 then the coefficient of non-determination is : [1 Mark, Dec. 2017]
(a) 0.4
(b) -0.6
(c) 0.36
(d) 0.64
Solution:
(d)
Co-efficient of Non-determination
= 1 – r² = 1 – (0.6)²
= 0.64

Question 38.
If there is a constant increase in the series then the obtained graph is : [1 Mark, Dec. 2017]
(a) Convex
(b) Concave
(c) Parabola
(d) Straight line from left to right
Solution:
(d)

Question 39.
If r = 0.58, correlation coefficient of u = -5x + 3 and v = y + 2 is __________: [1 Mark, June 2018]
(a) 0.58
(b) -0.58
(c) 0.62
(d) None
Solution:
(b)
The value of “r” does not change with respect to the change of origin and scale but sign may change.
So r_uv = – 0.58
[Note : Here; sign of x & y in both eqns. are opposite, so sign of “r” changes ].

Question 40.
If the sum of squares of deviations of ranks of 8 students is 50 then the rank correlation coefficient is _______: [1 Mark, June 2018]
(a) 0.40
(b) 0.45
(c) 0.5
(d) 0.8
Solution:
(a)
Given, N = 8; Σ D² = 50
R = 1 – \(\frac{6 \sum D^2}{N^3-N}\) = 1 – \(\frac{6 \times 50}{8^3-8}\) = 0.40

Question 41.
If the plotted points in a scatter diagram are evenly distributed, then the correlation is _________ [1 Mark, May 2018]
(a) Zero
(b) Negative
(c) Positive
(d) (a) or (b)
Solution:
(a)

Question 42.
The covariance between two variables is __________ [1 Mark, May 2018]
(a) Strictly positive
(b) Strictly negative
(c) Always Zero
(d) Either positive or negative or zero
Solution:
(d)

Question 43.
The coefficient of determination is defined by the formula [1 Mark, May 2018]
(a) r² = \(\frac{1-\text { unexplained variance }}{\text { total variance }}\)
(b) r² = \(\frac{\text { explained variance }}{\text { total variance }}\)
(c) both (a) and (b)
(d) None
Solution:
(c)

Question 44.
In the method of Concurrent Deviations, only the directions of change (Positive direction/Negative direction) in the variables are taken into account for calculation of [1 Mark, May 2018]
(a) Coefficient of S.D
(b) Coefficient of regression
(c) Coefficient of correlation
(d) None
Solution:
(c)

Question 45.
Correlation coefficient is ___________ of the units of measurement. [1 Mark, May 2018]
(a) dependent
(b) independent
(c) both
(d) None
Solution:
(b)

Question 46.
In case speed of an automobile and the distance required to stop the car after applying brakes correlation is …………… [1 Mark, May 2018]
(a) Positive
(b) Negative
(c) Zero
(d) None
Solution:
(a)

Question 47.
A relationship r² = 1 – \(\frac{500}{300}\) is not possible [1 Mark, May 2018]
(a) True
(b) False
(c) Both
(d) None
Solution:
(a) Given :
r² = 1 – \(\frac{500}{300}\) = \(\frac{-200}{300}\) is not possible [∵ r² is always positive]

Question 48.
Rank correlation coefficient lies between [1 Mark, May 2018]
(a) 0 to 1
(b) -1 to +1 inclusive of these values
(c) -1 to 0
(d) Both
Solution:
(b)

Question 49.
If the correlation coefficient between the variables X and Y is 0.5, then the correlation coefficient between the variables 2x – 4 and 3 – 2y is [1 Mark, Nov. 2018]
Solution:
(c)
Tricks : See Quicker BMLRS
Chapter: Correlation.
r. = -0.5 (Sign, of X & Y in both are opposite).

Question 50.
A.M. of regression coefficient is [1 Mark, June 2019]
(a) Equal to r
(b) Greater than or equal to r
(c) Half of r
(d) None
Solution:
(b)

Question 51.
Given that [1 Mark, June 2019]

Then Karl Pearson’s coefficient of correlation is
(a) Positive
(b) Zero
(c) Negative
(d) None
Solution:
(b)
If graph of this data is drawn then it will make a curvilinear relation. In this case r = 0
Hence Karl Pearson’s Coefficient of Correlation = r = “Zero”. Because it is equally distributed.

Question 52.
Find the probable error if r = \(\frac{2}{\sqrt{10}}\) and N = 36 [1 Mark, June 2019]
(a) 0.6745
(b) 0.067
(c) 0.5287
(d) None
Solution:
(b)
r = \(\frac{2}{\sqrt{10}}\) , N = 36, P.E = ?
Probable Error P.E = 0.6745 \(\frac{1-r^2}{\sqrt{N}}\)
= 0.06745\(\left[\frac{1-\left(\frac{2}{\sqrt{10}}\right)^2}{\sqrt{36}}\right]\) = 0.067 \(\frac{\left(1-\frac{4}{10}\right)}{6}\)

Question 53.
Given the following series : [1 Mark, June 2019]

The rank correlation coefficient R =

Solution:
(b)
Here two observations 15 & 16 has been repeated two times. So, we use the formula of the Rank Correlation Coefficient.

Question 54.
Determine Spearman’s rank correlation coefficient from the given data Σ D² = 30, N = 10 [1 Mark, June 2019]
(a) R = 0.82
(b) R = 0.32
(c) R = 0.40
(d) None of these
Solution:
(a)
Here, Σ D² =30, TV = 10
Spearman’s rank correlation
R = 1 – \(\frac{6 \sum D^2}{N\left(N^2-1\right)}\)
= 1 – \(\frac{6 \times 30}{10\left(10^2-1\right)}\) = 1 – \(\frac{180}{990}\) = 1 – \(\frac{2}{11}\) = \(\frac{9}{11}\)
= 0.82